Equazioni in C

Cos'è un'equazione in $\mathbb{C}$

Un equazione in $\displaystyle { \mathbb{C} }$ è un'equazione dove la nostra incognita, invece di essere un numero reale come al solito, è un numero complesso.

Cosa cambia?

Cambia che adesso otterremo altre soluzioni che prima ignoravamo. Prendiamo per esempio questa equazione di secondo grado:

• $\displaystyle { x^2 -x +2 =0 }$

Se andiamo a risolverla usando la formula risolutrice delle equazioni di secondo grado, notiamo che il Delta è negativo. Prima, quindi, vi sareste fermati ed avreste affermato "Quest'equazione è impossibile nei numeri reali".

Però, invece, nei numeri complessi è determinata. Infatti, il problema qui è di prendere la radice quadrata di un numero negativo, ma sappiamo benissimo che questo si può fare in $\displaystyle { \mathbb{C} }$

Quindi, risolviamo questa equazione:

$\displaystyle { x_{1;2}={-b \pm \sqrt{b^2 - 4ac}\over 2a}={1 \pm \sqrt{1-8} \over 2} }$ $\displaystyle { ={1\pm \sqrt{-7}\over 2} }$

A quanto equivale $\displaystyle { \sqrt{-7}? }$ Per la definizione di $\displaystyle { i, }$ è proprio uguale a $\displaystyle { \sqrt{7}i. }$ Se questo non vi è chiaro, vi consigliamo di andare a dare un'occhiata alla nostra lezione sui numeri immaginari (clicca qui 👈).

Dunque:

$\displaystyle { x_{1;2}={1\pm \sqrt{7}i \over 2} }$

Ed ecco risolta la nostra equazione.

Prima, quindi, siccome operavamo soltanto sui numeri reali, il numero di soluzioni di un'equazione poteva variare. Nei numeri complessi, invece, il Teorema fondamentale dell'algebra ci dice esattamente quante dobbiamo averne:

Teorema fondamentale dell'algebra

Il Teorema fondamentale dell'algebra è molto importante, altrimenti non si chiamerebbe "fondamentale". Esso afferma che un'equazione di grado n del tipo:

$\displaystyle { a_{n}x^n + a_{n-1}x^{n-1}+...+ }$ $\displaystyle { a_{2}x^2+a_{1}x+a_0=0 }$

Dove $\displaystyle { a_n }$ , $\displaystyle { a_{n-1} }$ , ecc. ... sono coefficienti complessi ha esattamente $\displaystyle { n }$ soluzioni nei numeri complessi (ovvero x deve essere un numero complesso), contando però ogni soluzione con la corrispettiva molteplicità.

Cosa significa contare ogni soluzione con la corrispettiva molteplicità? Significa che se per esempio abbiamo un'equazione di secondo grado dove il Delta è uguale a $\displaystyle { 0 }$ :

$\displaystyle { x^2 +2x + 1=0 }$

Quando andiamo a trovare le soluzioni:

$\displaystyle { x_{1;2}={-4\pm 0 \over 2} }$

Dobbiamo considerare sia la soluzione con il + che quella con il - , anche se, come in questo caso, sono uguali:

$\displaystyle { x_1={-4+0\over 2}=-2 }$

$\displaystyle { x_2={-4-0\over 2}=-2 }$

Quindi potrebbe sembrare che ci sia una sola soluzione, ma in realtà sono due coincidenti, cioè uguali. E' una grande differenza, perché altrimenti non saremmo capaci di applicare il Teorema fondamentale dell'algebra.

Radici dell'unità

A questo punto, però, vi potreste stare chiedendo: "ma se un'equazione di grado n ha sempre n soluzioni, perché un'equazione tipo $\displaystyle { x^3 =1 }$ ha solo una soluzione?"

La risposta è che quell'equazione, in realtà, non ha una sola soluzione e non si tratta nemmeno di tre soluzioni uguali. Per trovare le altre due, si potrebbe portare l' $\displaystyle { 1 }$ dall'altra parte, fattorizzare utilizzando la differenza di due cubi e risolvere l'equazione di secondo grado.

Ma adesso vogliamo cercare di risolverla in un altro modo. Un modo che ci permetterà di risolvere immediatamente qualsiasi equazione del tipo $\displaystyle { x^n = 1 }$ e cercheremo di farvi capire geometricamente cosa sta succedendo.

Risolvendola otteniamo:

$\displaystyle { x=\sqrt[3]{1} }$

Fino a qua è tutto giusto, ma il problema è che $\displaystyle { 1 }$ non è l'unica radice terza di $\displaystyle { 1 }$ . Altrimenti questo paragrafo non si chiamerebbe "radici dell'unità" (unità in parole povere è 1).

Infatti la radice n-esima di 1 ha n risultati. Come trovarli? Dobbiamo usare i numeri complessi. Potremmo anche usare i numeri complessi in forma trigonometrica, ma risulta più utile usarli in forma esponenziale. In caso non vi ricordaste bene questa forma, potete studiarla nella nostra lezione (clicca qui 👈).

Quindi scriviamo $\displaystyle { 1 }$ in forma esponenziale. Potremmo scrivere:

$\displaystyle { 1=e^{0i} }$

ma sarebbe sbagliato, perché essendo la funzione $\displaystyle { e^{ix} }$ una funzione periodica con periodo $\displaystyle { 2\pi }$ , per ottenere tutte le soluzioni dobbiamo aggiungere multipli di $\displaystyle { 2\pi }$ all'argomento:

$\displaystyle { 1=e^{(2k\pi +0)i}=e^{2k\pi i} }$

Dove $\displaystyle { k }$ è un numero intero.

Se, infatti, imponiamo $\displaystyle { k=2 }$ , otteniamo:

$\displaystyle { e^{2\cdot 2 \cdot \pi i}= e^{4\pi i}= e^{4\pi i - 2\pi i}=e^{2\pi i}=1 }$

Abbiamo usato il fatto che se sottraiamo $\displaystyle { 2\pi }$ dall'argomento, geometricamente è come fare un giro completo all'indietro, quindi torniamo sullo stesso esatto punto.

Quindi, aggiungere multipli di $\displaystyle { 2\pi }$ non cambia niente nel valore della potenza, infatti è sempre uguale a $\displaystyle { 1 }$ , ma facendo variare $\displaystyle { k }$ potremo trovare le altre soluzioni, altrimenti avremmo solo trovato $\displaystyle { x=1 }$ .

Dunque sostituendo nell'equazione:

$\displaystyle { x=\sqrt[3]{e^{2k\pi i}} }$

Possiamo usare le proprietà delle radici per semplificare:

$\displaystyle { x=e^{2k\pi i \over 3} }$

Adesso, quindi, non sommiamo più multipli di $\displaystyle { 2\pi }$ , ma multipli di $\displaystyle { 2\pi \over 3 }$, perché abbiamo preso la radice ed è per questo che troveremo $\displaystyle { 3 }$ soluzioni diverse.

Infatti, se imponiamo $\displaystyle { k=0 }$ , otteniamo:

$\displaystyle { x=e^{2\cdot 0 \cdot \pi i \over 3}= e^0 = 1 }$

Se però imponiamo $\displaystyle { k=1 }$ , otteniamo:

$\displaystyle { x=e^{2\cdot 1 \cdot \pi i \over 3}= e^{2\pi i \over 3} }$

Che è un numero diverso. Se imponiamo $\displaystyle { k=2 }$ , otteniamo:

$\displaystyle { e^{2\cdot 2 \cdot \pi i \over 3}=e^{4\pi i \over 3} }$

Che è un numero diverso ancora. Abbiamo però detto che dobbiamo ottenere esattamente $\displaystyle { 3 }$ soluzioni, quindi cosa succede se mettiamo $\displaystyle { k=3 }$? Vediamo:

$\displaystyle { e^{2\cdot 3\cdot \pi i \over 3}= e^{6\pi i \over 3}=e^{2\pi i}= 1 }$

Riotteniamo la prima soluzione. Se infatti continuiamo a sommare $\displaystyle { 2\pi \over 3 }$ , dopo esattamente $\displaystyle { 3 }$ volte avremo sommato $\displaystyle { 2\pi }$ , dunque torniamo al punto di partenza e riotteniamo la prima soluzione.

Vediamo nel piano complesso cosa sta succedendo. Prendiamo tutte e $\displaystyle { 3 }$ le soluzioni. Siccome hanno modulo pari ad $\displaystyle { 1 }$ , si troveranno nel cerchio di raggio $\displaystyle { 1 }$, chiamato cerchio unitario del piano complesso, e formeranno un angolo pari al loro argomento con l'asse reale.

Se questo non vi è chiaro, vi consigliamo di andare a ripassare la nostra lezione sui numeri complessi in forma esponenziale (clicca qui 👈).

Ecco dove stanno le soluzioni:

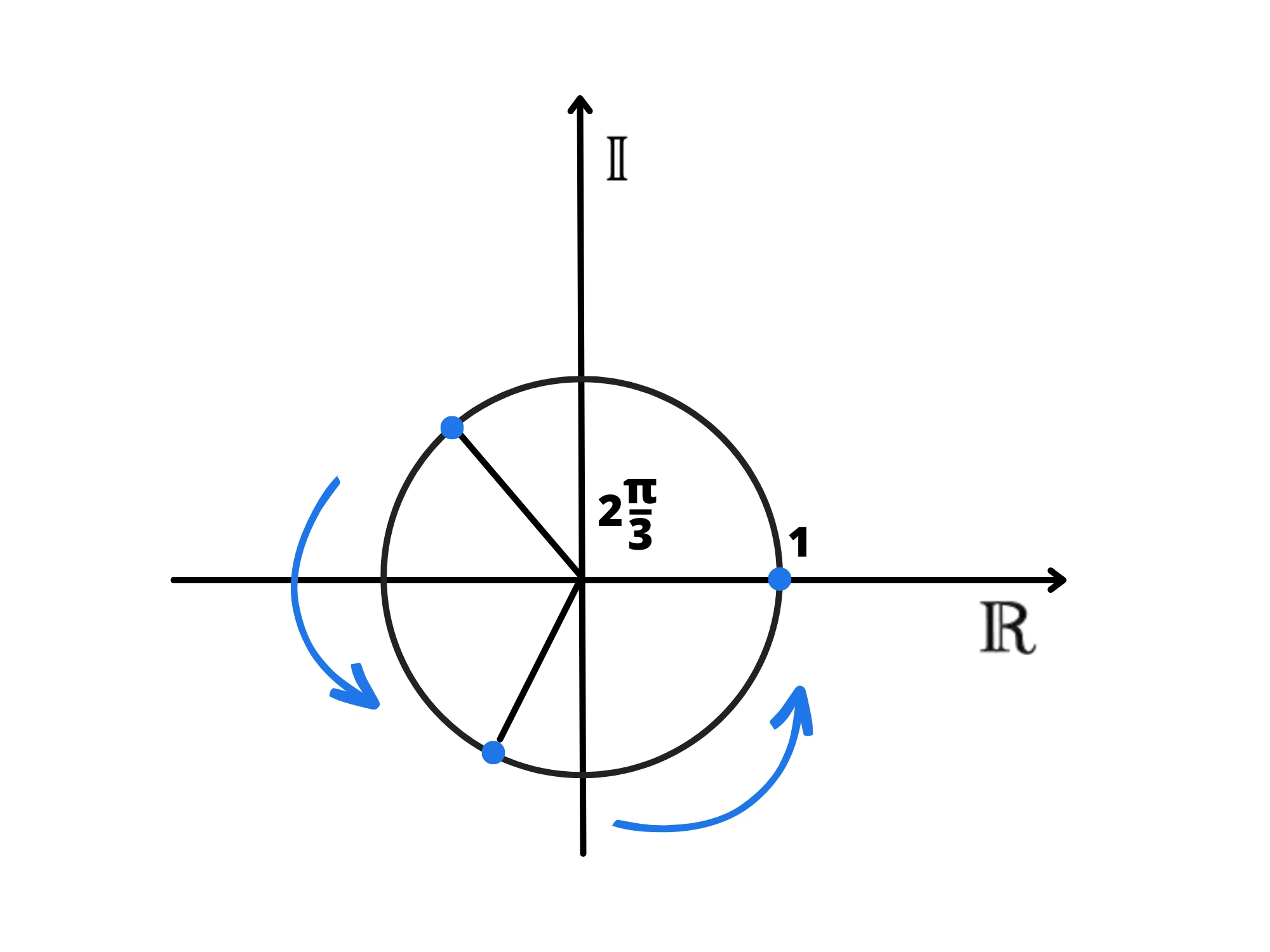
e tre soluzioni dividono esattamente la circonferenza in $\displaystyle { 3 }$ parti uguali. Sappiamo infatti che moltiplicare due numeri complessi in forma esponenziale equivale a moltiplicare i moduli e sommare gli argomenti, quindi siccome qui hanno modulo $\displaystyle { 1 }$ , moltiplicare due numeri sulla circonferenza unitaria equivale a sommare gli angoli.

Dunque se prendo il punto che si trova a un terzo della circonferenza, e lo elevo alla terza, equivale a sommare il suo angolo tre volte. Quindi arriveremo esattamente ad $\displaystyle { 1 }$.

Se prendo il punto a due terzi della circonferenza e lo elevo alla terza, equivale a sommare il suo angolo tre volte, ovvero a moltiplicarlo per $\displaystyle { 3 }$. Dunque tutti gli angoli del tipo $\displaystyle { 2\pi n\over 3 }$ arriveranno a $\displaystyle { 1 }$, perché elevare il numero complesso alla terza significa sommare $\displaystyle { 3 }$ volte l'angolo, che però equivale a moltiplicare l'angolo per $\displaystyle { 3 }$. Perciò il denominatore si semplifica e otteniamo un multiplo di $\displaystyle { 2\pi }$ , arrivando così a $\displaystyle { 1 }$.

Quindi, se abbiamo un'equazione del tipo $\displaystyle { x^n = 1 }$ , riscriviamo $\displaystyle { 1 }$ in forma esponenziale e prendiamo la radice:

$\displaystyle { x=\sqrt[n]{e^{2k\pi i}} }$

quindi semplifichiamo:

$\displaystyle { x=e^{2k\pi i \over n} }$

e facendo variare $\displaystyle { k }$ da $\displaystyle { 0 }$ ad $\displaystyle { n }$ otteniamo tutte le soluzioni. Geometricamente, quello che stiamo facendo è prendere la circonferenza unitaria e dividerla in $\displaystyle { n }$ parti uguali partendo da $\displaystyle { 1 }$ , ottenendo $\displaystyle { n }$ punti che saranno proprio le soluzioni.

Equazioni del tipo $x^n=c$

Adesso che sappiamo come risolvere equazioni del tipo $\displaystyle { x^n=1 }$ , vediamo cosa succede se al posto di $\displaystyle { 1 }$ mettiamo un numero complesso in generale.

$\displaystyle { 1 }$ si comportava particolarmente bene ed era facile da lavorarci, ma possiamo risolvere questo tipo di equazioni anche se la costante è qualsiasi altro numero complesso.

Vediamo come fare:

Supponiamo di avere $\displaystyle { c }$ in forma algebrica:

$\displaystyle { c=a+ib }$

Trasformiamolo in forma trigonometrica:

$\displaystyle { c= r\cdot [\cos(\theta)+i\sin(\theta)] }$

e quindi in forma esponenziale:

$\displaystyle { c=r\cdot e^{i\theta} }$

Pure questa volta, se prendessimo direttamente la radice, otterremmo soltanto una soluzione e mancheremmo le altre $\displaystyle { n-1 }$ soluzioni. Per risolvere questo problema, anche questa volta aggiungiamo multipli di $\displaystyle { 2\pi }$ all'argomento:

$\displaystyle { c=re^{(\theta + 2k\pi)i} }$

E solo adesso prendiamo la radice:

$\displaystyle { x=\sqrt[n]{re^{(\theta + 2k\pi)i}} }$

Usiamo le proprietà delle potenze per semplificare:

$\displaystyle { x=\sqrt[n]{r} \cdot e^{(\theta + 2k\pi)i\over n} }$

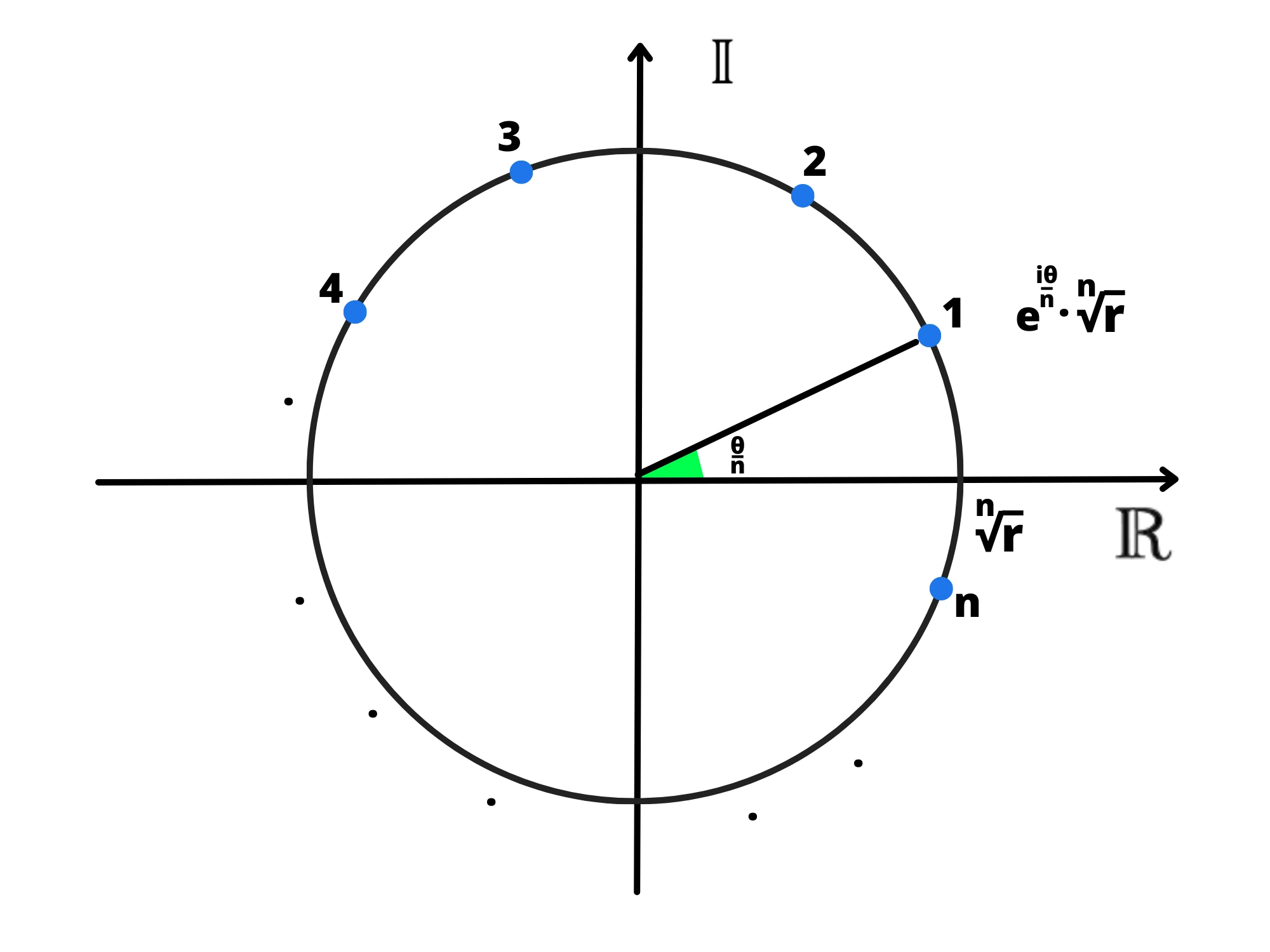
Ed ecco trovate tutte e $\displaystyle { n }$ le soluzioni, ma cosa significano geometricamente?

Usiamo le proprietà delle potenze per dividere la potenza in due:

$\displaystyle { x=\sqrt[n]{r} \cdot e^{\theta i\over n} \cdot e^{2k\pi i\over n} }$

Il primo fattore, $\displaystyle { \sqrt[n] {r}, }$ equivale al modulo della soluzione (siccome gli altri due fattori sono del tipo $e^{ix}$, essi hanno modulo pari ad $\displaystyle { 1 }$ ). Siccome al variare di $\displaystyle { k }$ il modulo non cambia, vuol dire che tutti i punti avranno la stessa distanza dal centro.

In altre parole, si trovano sulla circonferenza incentrata all'origine e con raggio pari a $\displaystyle { \sqrt[n]{r} }$ .

L'ultimo fattore equivale alla $\displaystyle { k }$ -esima radice dell'unità. Quindi equivale anche questa volta a dividere la circonferenza in $\displaystyle { n }$ parti uguali. Però questa volta non iniziamo da un punto sull'asse reale, come avevamo fatto prima con $\displaystyle { 1 }$ . Questo perché non dobbiamo dimenticarci della presenza del secondo fattore.

Essendo della forma $\displaystyle { e^{ix} }$ , come abbiamo visto nel paragrafo precedente, la moltiplicazione per esso equivale a sommare $\displaystyle { x }$ radianti all'angolo del numero che stiamo moltiplicando.

Quindi se non ci fosse stato lui, saremmo partiti dal punto con modulo $\displaystyle { \sqrt[n]{r} }$ sull'asse reale, ovvero $\displaystyle { \sqrt[n]{r} }$ , avremmo diviso la circonferenza in $\displaystyle { n }$ parti e i punti trovati sarebbero state le soluzioni. Ma, siccome è presente questo ulteriore fattore, preso il punto sull'asse reale $\displaystyle { \sqrt[n]{r} }$ , dobbiamo ruotare in senso antiorario di $\displaystyle { \theta\over n }$ radianti e partendo da quel punto cominciare a dividere la circonferenza: