Numeri complessi in forma trigonometrica

Cos'è la forma trigonometrica dei numeri complessi?

Come sapete bene, la retta dei numeri ci permette di rappresentare qualsiasi numero reale. In essa però non c'è spazio per i numeri complessi.

Quale punto della retta corrisponde a $\displaystyle { 2+3i }$? Potete cercare quanto volete ma non troverete nessun posto dove metterlo.

Per rappresentare i numeri complessi, dobbiamo aumentare il numero di dimensioni. La retta dei numeri reali diventa l'asse $\displaystyle { x }$ del piano e mettiamo i numeri immaginari sull'asse $\displaystyle { y }$ :

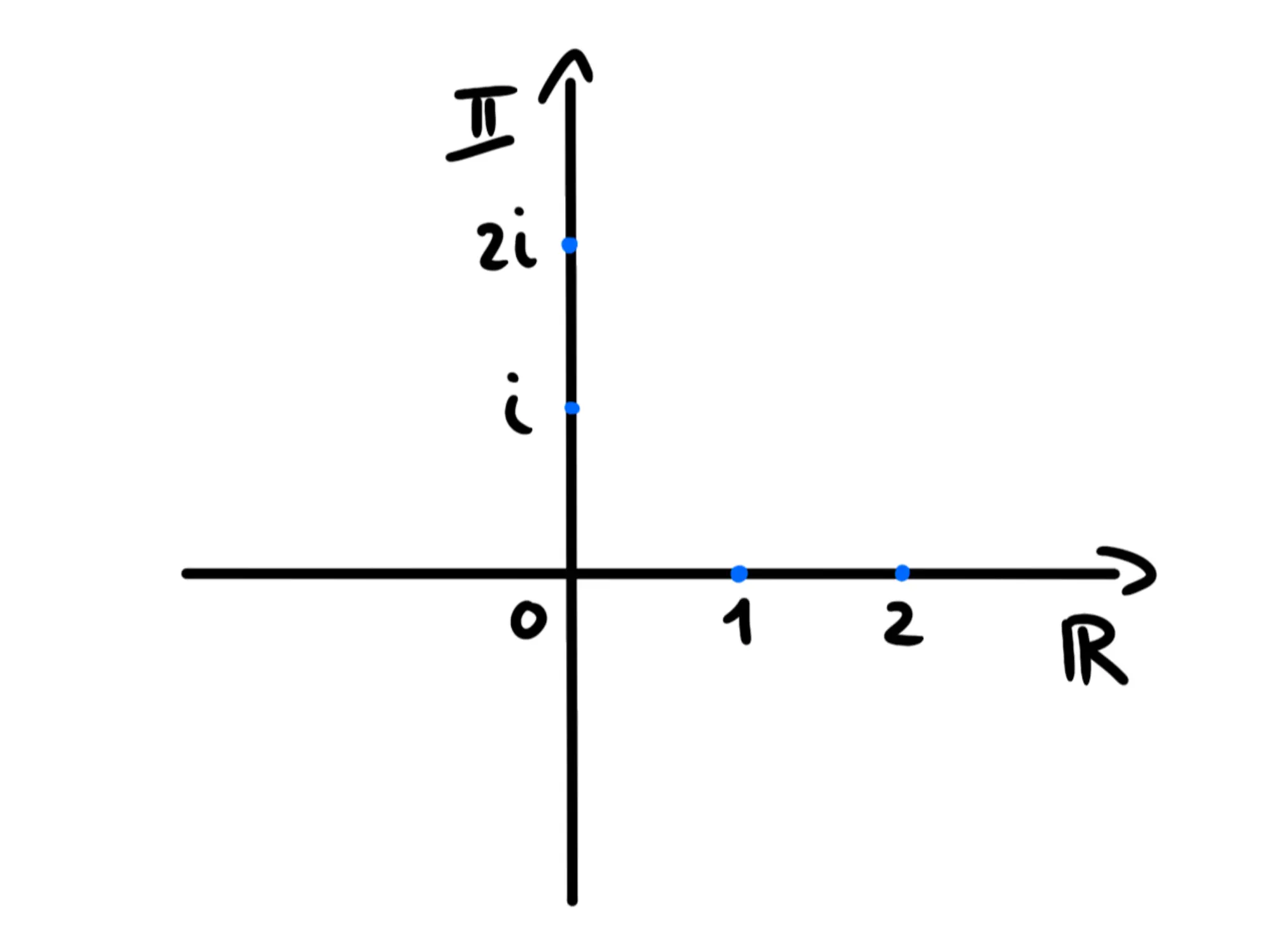
Ora, associamo ogni numero complesso $\displaystyle { z=a+ib }$ al punto di coordinate $\displaystyle { (a;b) }$:

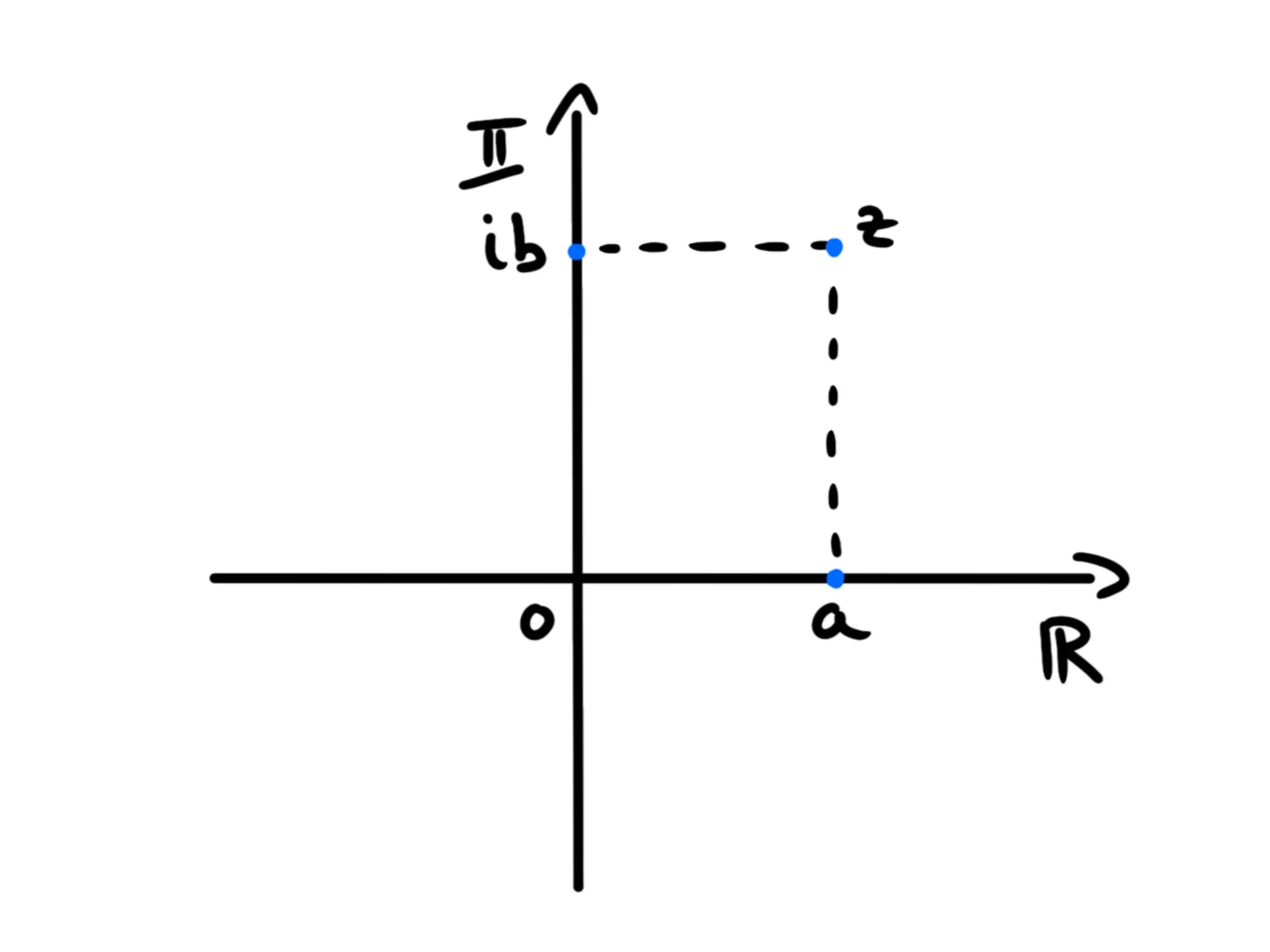
Questo piano viene talvolta chiamato piano di Argand-Gauss, qualche volta solo piano di Gauss ed altre volte piano complesso. Comunque lo si voglia chiamare, questo piano ci permette di rappresentare geometricamente i numeri complessi.

Guardando al piano complesso si nota meglio anche come i numeri reali siano dei casi particolari di numeri complessi. La retta dei numeri reali è infatti la retta con tutti i punti con parte immaginaria nulla.

Possiamo usare il piano di Gauss e la trigonometria per esprimere in un modo alternativo i numeri complessi. Notiamo infatti che preso un numero complesso $\displaystyle { z=a+ib }$ (a cui corrisponde il punto $\displaystyle { (a;ib) }$ ), esso formerà un angolo $\displaystyle { \theta }$ con l'asse dei numeri reali e sarà ad una certa distanza $\displaystyle { r }$ dall'origine:

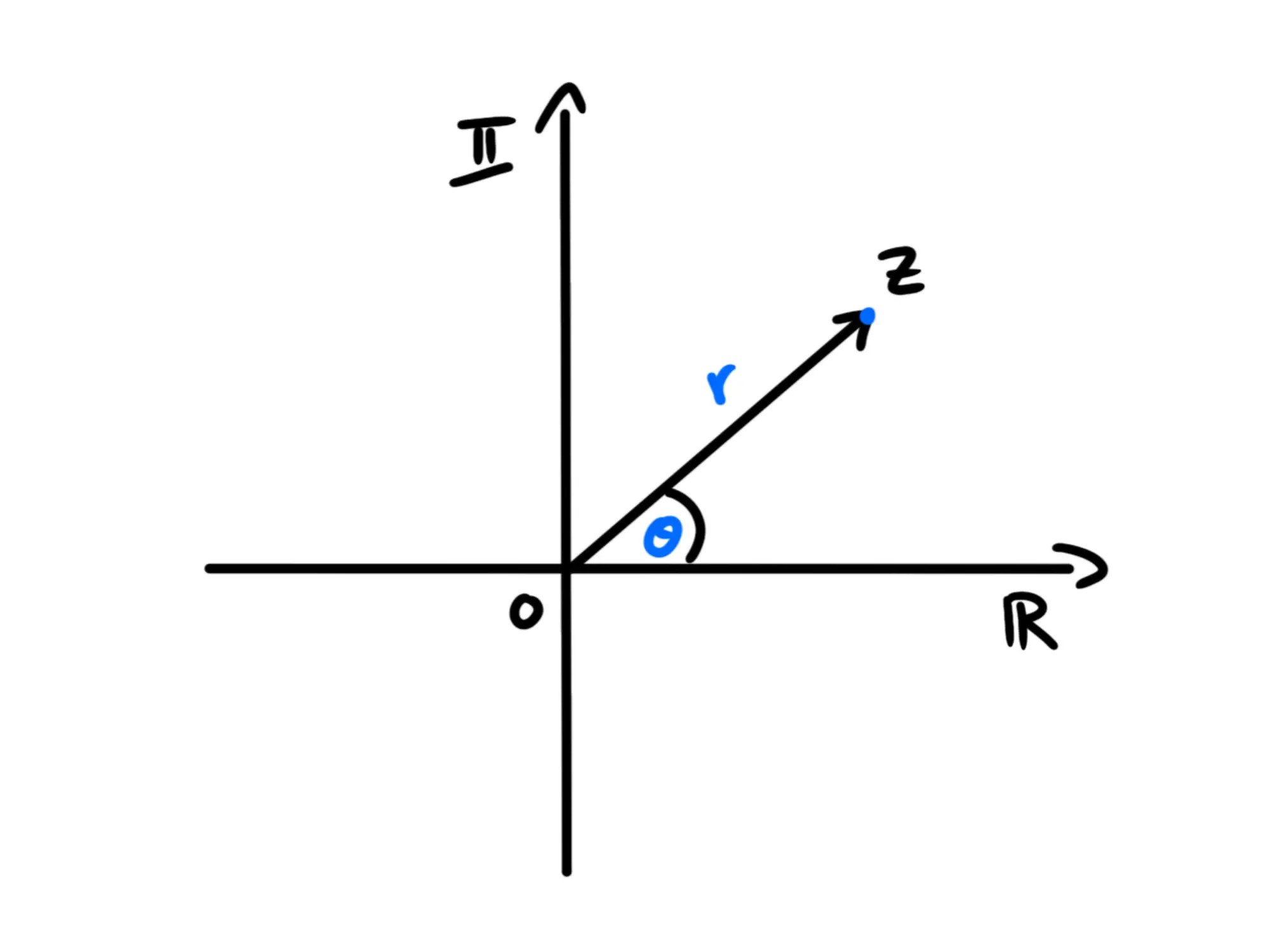
Proiettando il punto sull'asse dei numeri reali otteniamo un triangolo rettangolo:

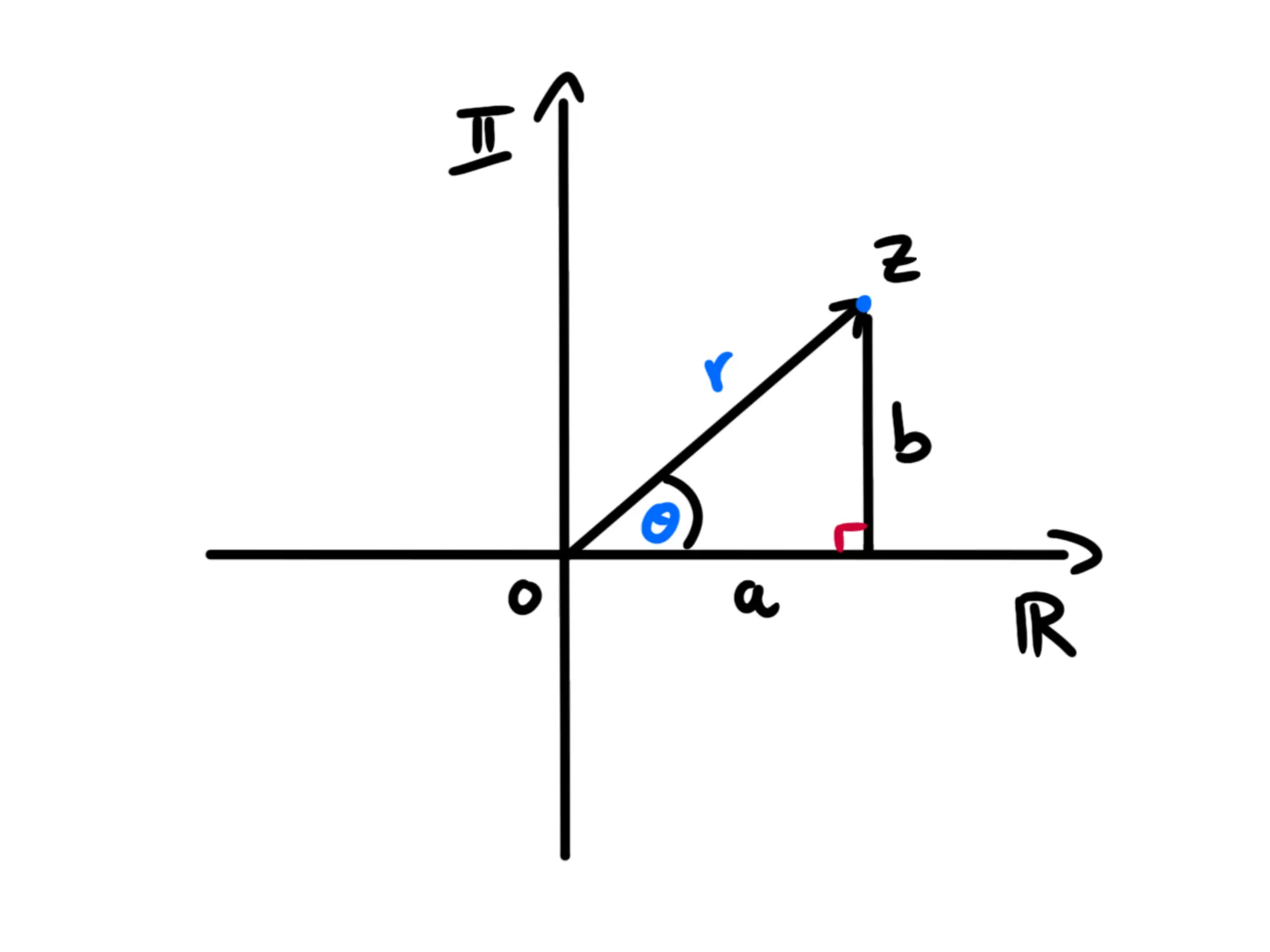
Usando il teorema di Pitagora abbiamo:

$\displaystyle { r=\sqrt{a^2+b^2} }$

Mentre usando la trigonometria abbiamo:

$\displaystyle { a=r\cos(\theta) }$

$\displaystyle { b=r\sin(\theta) }$

Possiamo quindi sostituire questi nuovi valori di $\displaystyle { a }$ e $\displaystyle { b }$ nella forma algebrica di $\displaystyle { z }$ per ottenere la sua forma trigonometrica:

$\displaystyle { z=a+ib= r\cos(\theta) + ir\sin(\theta) = }$ $\displaystyle { r[\cos(\theta) + i\sin(\theta)] }$

$\displaystyle { r }$ viene chiamato il modulo di $\displaystyle { z }$ , mentre $\displaystyle { \theta }$ è l'argomento.

Usando le formule trovate prima potete tramutare un numero complesso dalla sua forma algebrica a quella trigonometrica e viceversa.

Apparentemente la forma trigonometrica può sembrare più scomoda di quella algebrica, ma talvolta è più comoda da usare nelle operazioni e in futuro ci servirà per passare alla forma esponenziale, che è invece molto utile.

Operazioni

Quando sommiamo due numeri complessi scritti in forma trigonometrica, l'unica cosa che possiamo fare è raggruppare la parte reale da una parte e quella immaginaria dall'altra:

$\displaystyle { z=r_1 [\cos(\theta_1) + i\sin(\theta_1)] }$

$\displaystyle { w=r_2 [\cos(\theta_2) + i\sin(\theta_2)] }$

La moltiplicazione invece è più carina:

Il prodotto di due numeri complessi è uguale ad un numero complesso con modulo il prodotto dei moduli e con argomento la somma degli argomenti:

$\displaystyle { z= r_1 [\cos(\theta_1) + i\sin(\theta_1)] }$

$\displaystyle { w=r_2 [\cos(\theta_2) + i\sin(\theta_2)] }$

La divisione di due numeri complessi è un numero complesso con modulo il rapporto tra i moduli e con argomento la differenza degli argomenti:

$\displaystyle { z= r_1 [\cos(\theta_1) + i\sin(\theta_1)] }$

$\displaystyle { w=r_2 [\cos(\theta_2) + i\sin(\theta_2)] }$

L'n-esima potenza di un numero complesso è un numero complesso con modulo l'ennesima potenza del modulo e con argomento $\displaystyle { n\theta }$ :

$\displaystyle { z= r [\cos(\theta) + i\sin(\theta)] }$

Infine, per ottenere il coniugato di $\displaystyle { z=r[\cos(\theta) + i \sin(\theta)], }$ basterà, per definizione, mettere un segno meno davanti alla parte immaginaria, cioè davanti al seno, ottenendo: