Teorema di Lagrange

Teorema di Lagrange

Il teorema di Lagrange viene spesso visto come una generalizzazione del teorema di Rolle (che abbiamo visto qui 👈). Infatti, esso enuncia che:

Se una funzione $\displaystyle { f(x) }$ è continua e derivabile in un intervallo chiuso e limitato $\displaystyle { [a,b], }$ allora esiste un punto c in quell'intervallo tale che:

Il rapporto che troviamo a destra, per definizione, altro non è che il coefficiente angolare della retta passante per i punti $\displaystyle { (a;f(a)) }$ e $\displaystyle { (b;f(b)). }$

Per la definizione di derivata, poi, $\displaystyle { f'(c) }$ è il coefficiente angolare della retta tangente alla funzione $\displaystyle { f(x) }$ in $\displaystyle { c. }$

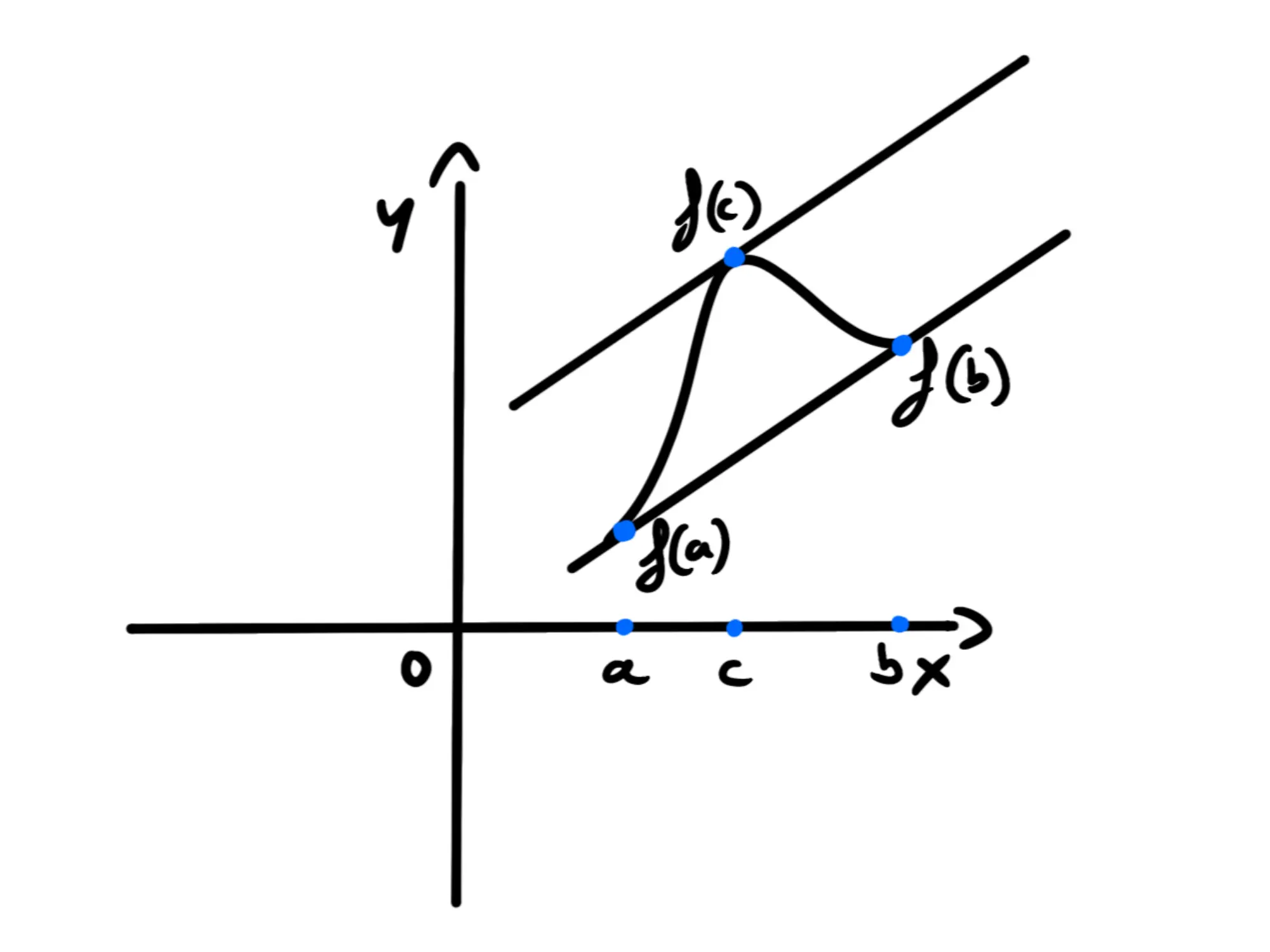
Quindi, dire che questi due coefficienti angolari sono uguali, vuol dire, per la definizione di parallelismo, che la tangente a $\displaystyle { c }$ è parallela alla retta passante per quei due punti:

Nel caso in cui $\displaystyle { f(a)=f(b), }$ riotteniamo il teorema di Rolle, per questo si tratta di una sua generalizzazione. Dimostriamo ora questo teorema.

Definiamo la seguente funzione:

$\displaystyle { g(x) = f(x) - kx }$

Siccome sia $\displaystyle { f(x) }$ che $\displaystyle { kx }$ sono due funzioni continue e derivabili, anche $\displaystyle { g(x) }$ lo dovrà essere.

Ora, a cosa ci serve questa nuova funzione? e quanto vale $\displaystyle { k? }$

Questa funzione sarà molto utile perché sceglieremo un $\displaystyle { k }$ tale che:

$\displaystyle { k= {f(b)-f(a)\over b-a} }$

Se andiamo ad espandere otteniamo:

$\displaystyle { (b-a)k = f(b) - f(a) }$

$\displaystyle { f(a) - ka = f(b) - kb }$

Sostituendo con $\displaystyle { g(x) }$ otteniamo:

$\displaystyle { g(a)=g(b) }$

Cioè, la funzione $\displaystyle { g(x) }$ soddisfa le condizioni per poter applicare il teorema di Rolle. Questo, quindi, è stato possibile perché potevamo scegliere qualsiasi numero reale per $\displaystyle { k. }$

Notate che $\displaystyle { a }$ e $\displaystyle { b }$ sono i due estremi di un intervallo chiuso e limitato, dunque non possono essere uguali, quindi $\displaystyle { b-a }$ deve essere diverso da $\displaystyle { 0 }$ e non ci sono quindi problemi di esistenza.

Ora sostituiamo $\displaystyle { k }$ nell'equazione per $\displaystyle { g(x): }$

$\displaystyle { g(x) = f(x) - kx }$

$\displaystyle { g(x) = f(x) - {f(b)-f(a)\over b-a}x }$

e prendiamo la derivata da entrambi i lati:

$\displaystyle { g'(x) = f'(x) - {f(b)-f(a)\over b-a} }$

Ora, però, siccome $\displaystyle { g(x) }$ soddisfava le condizioni per poter applicare il teorema di Rolle, deve esserci un punto $\displaystyle { c }$ tale che $\displaystyle { g'(c) = 0. }$ Quindi otteniamo:

$\displaystyle { g'(c) = f'(c) - {f(b)-f(a)\over b-a} }$

$\displaystyle { 0= f'(c) - {f(b)-f(a)\over b-a} }$

$\displaystyle { f'(c) = {f(b)-f(a)\over b-a} }$

Ed ecco dimostrato il teorema di Lagrange.