Parabola

Cos'è una parabola?

Una parabola è il luogo geometrico dei punti equidistanti da un punto $\displaystyle { F }$ ed una retta $\displaystyle { d. }$

Questo punto fisso $\displaystyle { F }$ viene chiamato fuoco, mentre la retta $\displaystyle { d }$ è detta direttrice.

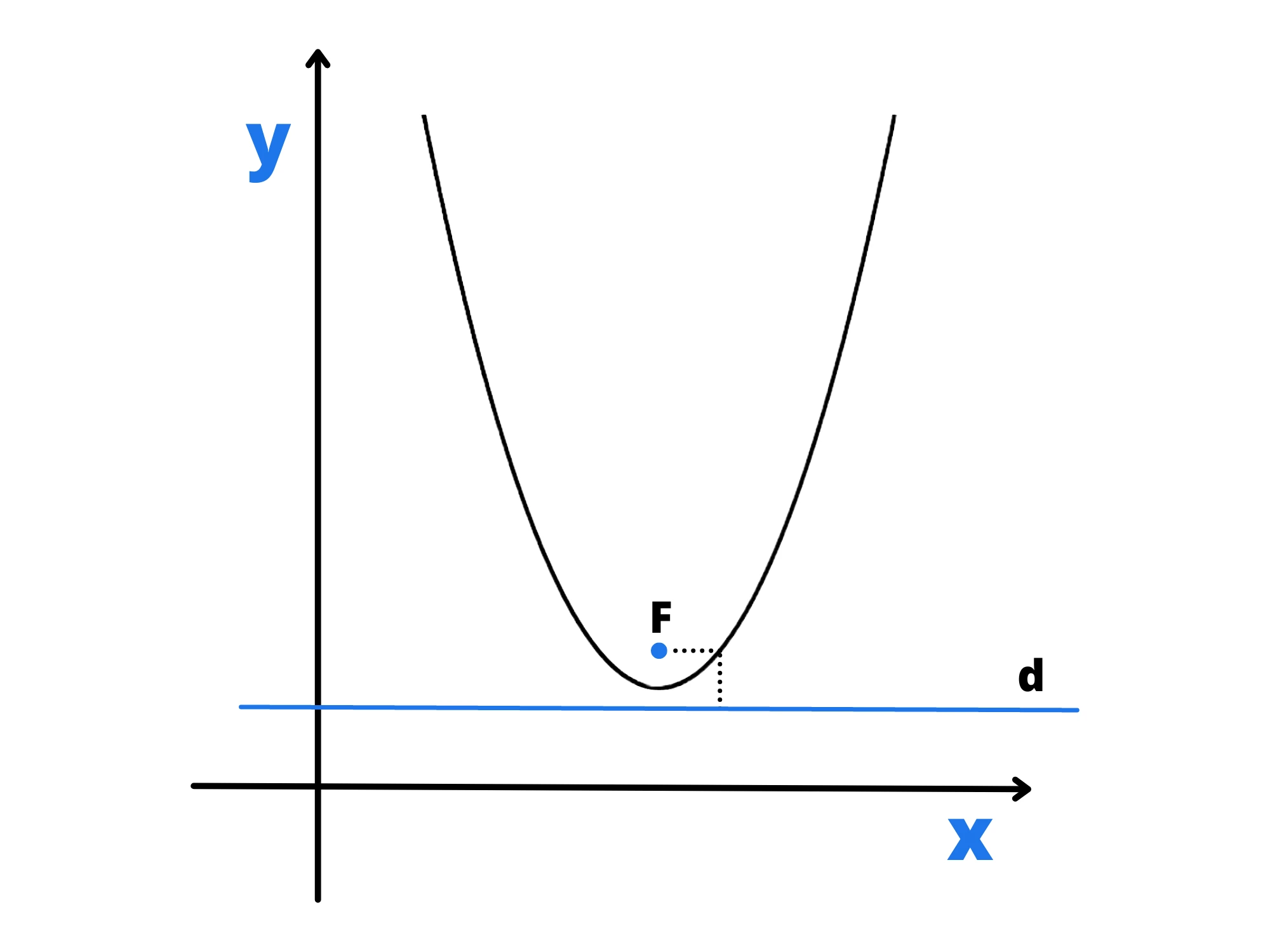
La retta passante per il fuoco e perpendicolare alla direttrice si chiama asse della parabola. Essa è anche l’asse di simmetria della parabola.

Il vertice della parabola è il punto di intersezione della parabola con l’asse e lo indichiamo con la lettera $V.$

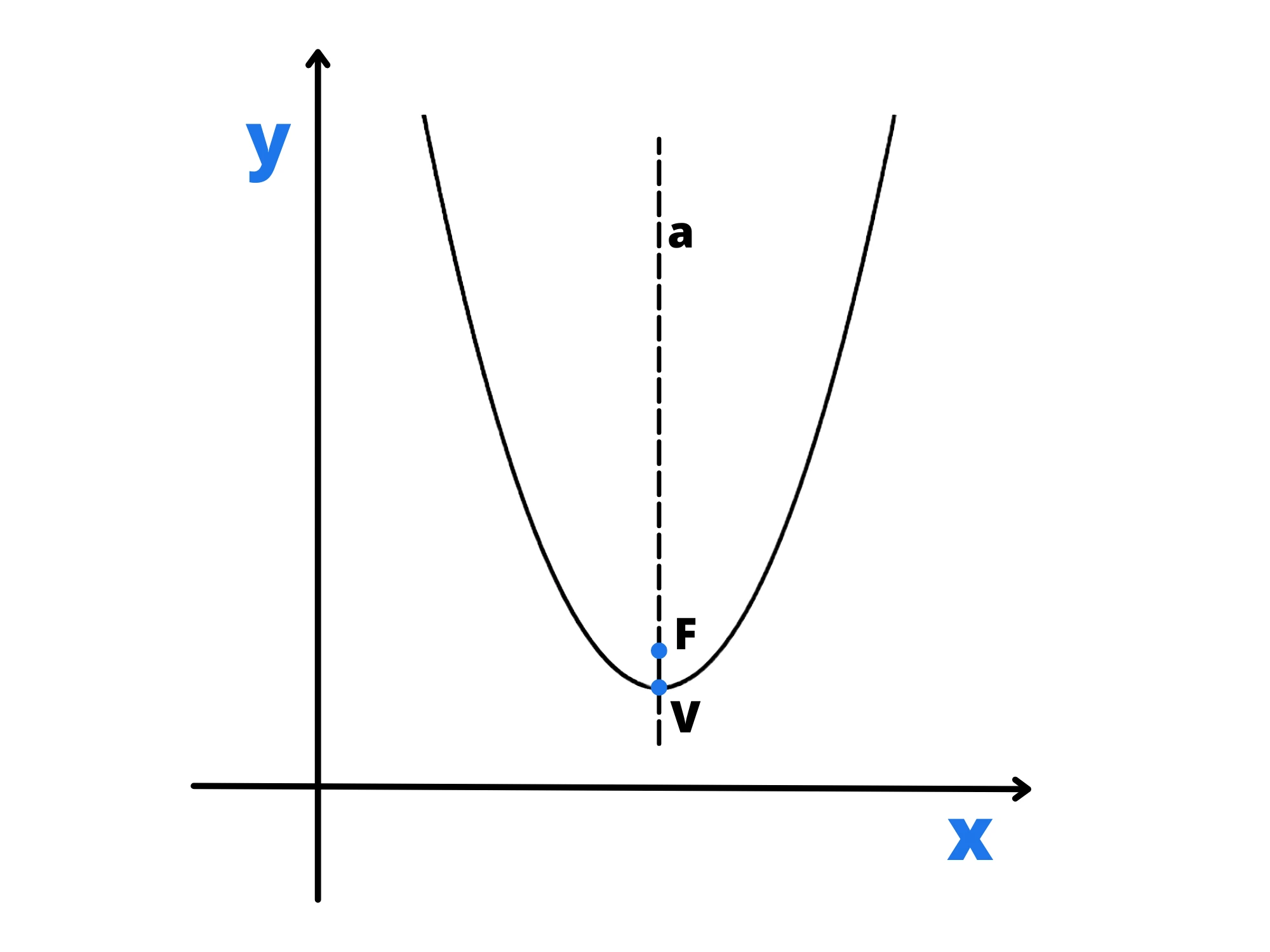
Il vertice è, insomma, il punto più alto o più basso della parabola, a seconda di come è rivolta.

In generale una parabola si indica con una lettera greca minuscola, solitamente con $\displaystyle { \gamma }$ (gamma), ma possono anche essere usate altre lettere.

Perché ci interessano molto le parabole?

Perché, come vedremo tra poco, la parabola è descritta da un'equazione di secondo grado e questo la rende molto comune da incontrare e anche molto utile nella risoluzione di alcuni problemi, come le disequazioni di secondo grado.

Abbiamo detto che si tratta di un luogo geometrico, ma la parabola è anche una funzione?

La parabola è una funzione quando la direttrice è orizzontale.

Quando la direttrice non è orizzontale, la parabola è inclinata o totalmente orizzontale. In questo caso ad una $\displaystyle { x }$ corrispondono più $y$ e quindi la parabola non è una funzione.

Parabola con asse coincidente con l’asse y e vertice nell’origine

Proviamo a trovare l'equazione di una parabola. Per farlo, iniziamo dal caso più semplice, cioè quello di una parabola con asse coincidente all’asse delle $\displaystyle { y }$ e con vertice nell’origine.

Notiamo che il fuoco della parabola è un punto dell’asse delle $\displaystyle { y }$ e che per questo avrà coordinate $\displaystyle { (0, f) }$ , con $\displaystyle { f\neq 0 }$. (perché il fuoco si trova sempre sull'asse della parabola e in questo caso l'asse della parabola è l'asse $\displaystyle { y }$ )

La direttrice, per definizione, è perpendicolare all’asse della parabola e per questo deve essere parallela all’asse delle $\displaystyle { x }$ .

Quindi, la direttrice interseca l’asse delle $\displaystyle { y }$ in un punto $\displaystyle { D }$ e questo, visto che il vertice deve essere equidistante dal fuoco e dalla direttrice, avrà coordinate $\displaystyle { (0;-f) }$ .

L’equazione della direttrice sarà quindi:

$\displaystyle { y = -f }$

Ora prendiamo un punto generico della parabola $\displaystyle { P(x,y) }$ e cerchiamo le distanze $\displaystyle { \overline{PF} }$ e $\displaystyle { \overline{PH} }$ rispettivamente dal fuoco e dalla direttrice, dove $\displaystyle { H }$ è il piede della distanza che parte da $\displaystyle { P }$ .

$\displaystyle { \overline{PF}= }$ $\displaystyle { \sqrt{(x-0)^2+(y-f)^2} = }$ $\displaystyle { \sqrt{x^2+(y-f)^2} }$

$\displaystyle { \overline{PH}= |y+f| }$

Per la definizione della parabola queste due distanze devono essere uguali:

$\displaystyle { \sqrt{x^2+(y-f)^2} = |y+f| }$

$\displaystyle { \longrightarrow x^2+(y-f)^2 = (y+f)^2 }$ $\displaystyle { \longrightarrow }$ $\displaystyle { x^2-4yf=0 }$

Ora isoliamo la $\displaystyle { y }$ e ricaviamo l’equazione $\displaystyle { y= \frac{1}{4f} x^2 }$ . Per semplificare un po’ l’equazione, poniamo $\displaystyle { a=\frac{1}{4f} }$ e otteniamo

$\displaystyle { y=ax^2 }$

che sarà dunque l’equazione generica di una parabola con asse coincidente con l’asse delle $\displaystyle { y }$ e con vertice nell’origine.

Per concludere troviamo alcune formule significative che potrebbero risultare utili nei problemi.

Partendo dalla relazione $\displaystyle { a=\frac{1}{4f} }$ otteniamo $\displaystyle { f=\frac{1}{4a} }$ e da questa possiamo ricavare le coordinate del fuoco e l'equazione della direttrice:

Coordinate del fuoco $\displaystyle { F\bigg(0; \frac{1}{4a}\bigg) }$

Equazione della direttrice $\displaystyle { d=-\frac{1}{4a} }$

Parabola con asse parallelo all’asse y

Più in generale possiamo avere delle parabola il cui asse non coincide con l'asse $\displaystyle { y, }$ ma è solo parallelo ad esso. Ecco qualche esempio di grafici di questa tipologia di parabole:

Troviamo la loro equazione:

Siccome la direttrice è, per definizione, perpendicolare all'asse della parabola, allora dovrà pure essere perpendicolare all'asse $\displaystyle { y, }$ cioè sarà parallela all'asse $\displaystyle { x. }$

Dunque la sua equazione sarà della forma $\displaystyle { y=k. }$

Il fuoco avrà coordinate generiche $\displaystyle { (x_f; y_f). }$

Per la definizione della parabola, un punto generico $\displaystyle { P(x,y) }$ appartenente ad essa deve essere equidistande dal fuoco e dalla direttrice.

Per calcolare la distanza della direttrice, siccome si tratta di una retta parallela all'asse $\displaystyle { x, }$$\displaystyle { x, }$ ci basta calcolare il modulo della differenza della $\displaystyle { y }$ del punto e l' $\displaystyle { y }$ della retta:

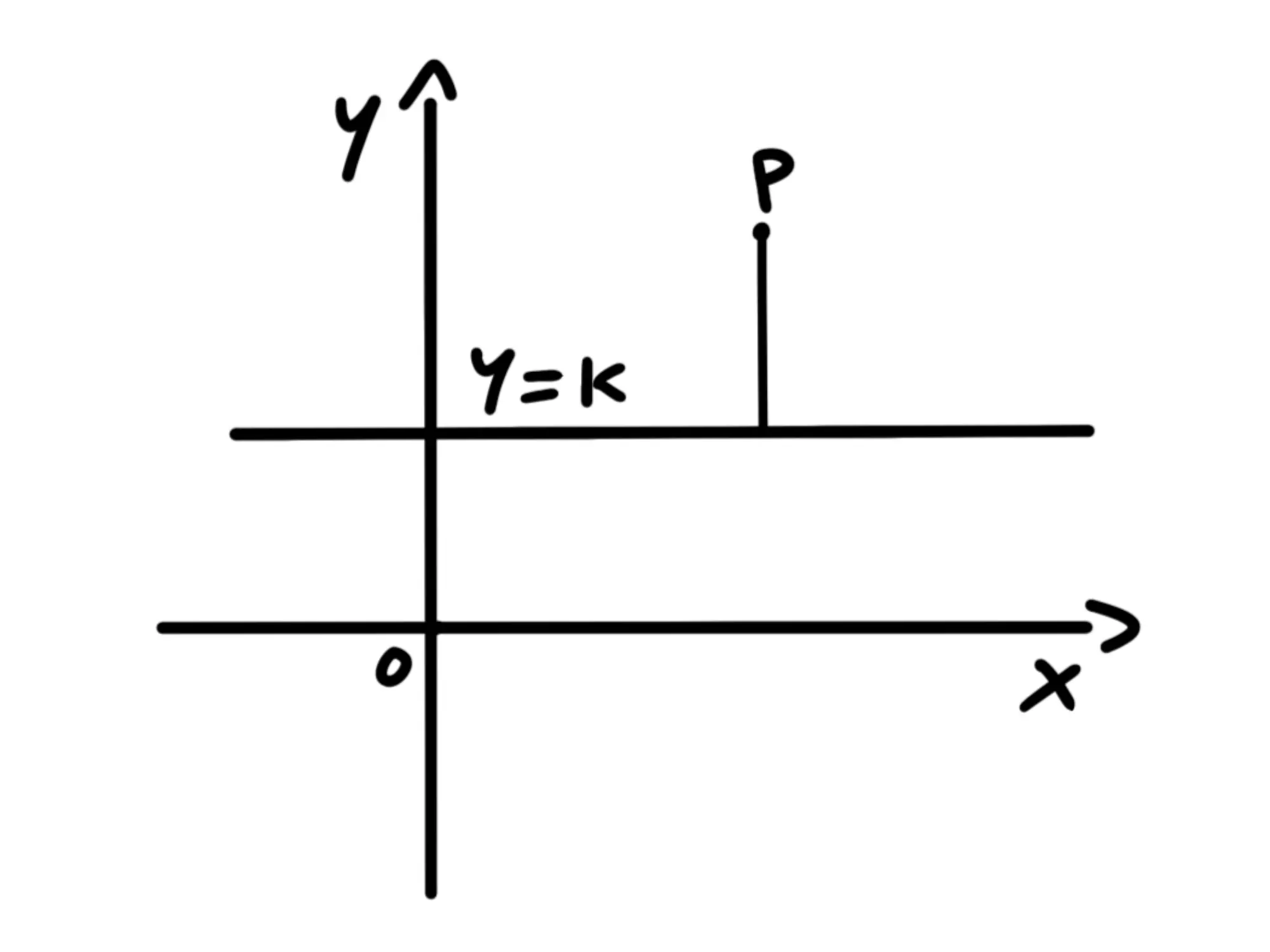
Quindi sarà uguale a $\displaystyle { |y-k|. }$

Per calcolare la distanza dal fuoco, invece, ci basta applicare la formula della distanza fra due punti, ottenendo $\displaystyle { \sqrt{(x-x_f)^2 - (y-y_f)^2}. }$

Queste due distanze devono appunto essere uguali, perciò otteniamo:

$\displaystyle { \sqrt{(x-x_f)^2 + (y-y_f)^2} = |y -k| }$

Abbiamo quantità positive da entrambi i lati e quella radice deve per forza esistere perché la somma di due quadrati è sempre maggiore o uguale a zero.

Perciò possiamo elevare entrambi i lati dell'equazione alla seconda:

$\displaystyle { \left(\sqrt{(x-x_f)^2 + (y-y_f)^2}\right)^2 = |y -k|^2 }$

$\displaystyle { (x-x_f)^2 + (y-y_f)^2= (y-k)^2 }$

Espandiamo e semplifichiamo:

$\displaystyle { x^2 - 2 x_fx + x_f^2 + y^2 -2y_fy + y_f^2 = y^2 - 2yk + k^2 }$

$\displaystyle { x^2 - 2x_fx + x_f^2 -2y_fy + y_f^2 = -2yk + k^2 }$

Isoliamo la $\displaystyle { y: }$

$\displaystyle { x^2 - 2x_fx + x_f^2 + y_2^2 - k^2 = 2y_fy - 2ky }$

$\displaystyle { x^2 - 2x_fx + x_f^2 + y_2^2 - k^2 = 2(y_f-k)y }$

$\displaystyle { {1\over 2(y_f -k)}x^2 - {x_f\over y_f -k}x + {x_f^2 + y_2^2 - k^2\over 2(y_f-k)} = y }$

Scambiamo i lati dell'equazione:

$\displaystyle { y={1\over 2(y_f -k)}x^2 - {x_f\over y_f -k}x + {x_f^2 + y_2^2 - k^2\over 2(y_f-k)} }$

Scritta in questo modo, però, è troppo complicata. Semplifichiamola cambiando i nomi delle costanti.

$\displaystyle { {1\over 2(y_f -k)} }$ lo richiamiamo $\displaystyle { a. }$

Poi $\displaystyle { -{x_f \over y_f - k} }$ lo chiamiamo $\displaystyle { b }$ ed infine $\displaystyle { {x_f^2 + y_f^2 - k^2 \over 2(y_f - k)} }$ lo chiamiamo $\displaystyle { c. }$

In questo modo la nostra equazione diventa:

Cioè l'equazione della parabola è espressa da un generico polinomio di secondo grado, come avevamo anticipato all'inizio.

Concavità e apertura

La concavità della parabola ci dice come è rivolta una parabola.

Se la parabola è rivolta verso l'alto, si dirà che ha concavità verso l'alto:

Mentre se è rivolta verso il basso, si dirà che ha concavità verso il basso:

Questo si può ricordare facilmente pensando a una faccina, se ricorda un sorriso sarà una parabola con concavità verso l’alto, mentre se assomiglia ad un broncio sarà invece una parabola con concavità verso il basso:

Come determinare, però, la concavità di una parabola conoscendo solo la sua equazione senza vedere il grafico?

In realtà, è semplicissimo: basta guardare al segno del coefficiente del termine di secondo grado.(Ovvero il coefficiente di $x^2$)

Se è positivo la parabola ha concavità verso l'alto, se è negativo la concavità è verso il basso.

Quindi $\displaystyle { y = 3x^2 - 3x -1 }$ ha concavità verso l'alto, mentre $\displaystyle { y=-x^2 + 2x - 7 }$ ha concavità verso il basso.

Dunque se la parabola ha equazione $\displaystyle { y=ax^2 + bx +c, }$ avrà concavità verso l'alto se $\displaystyle { a>0, }$ mentre avrà concavità verso il basso se $\displaystyle { a< 0. }$

Vertice

Esistono delle formule che ci fanno trovare molto velocemente le coordinate del vertice.

Vedremo prima la dimostrazione che solitamente si studia a scuola, che però è più lunga e meno generale, per poi vedere una dimostrazione alternativa molto più veloce.

Prendiamo quindi una parabola che interseca l'asse delle $\displaystyle { x }$ due volte:

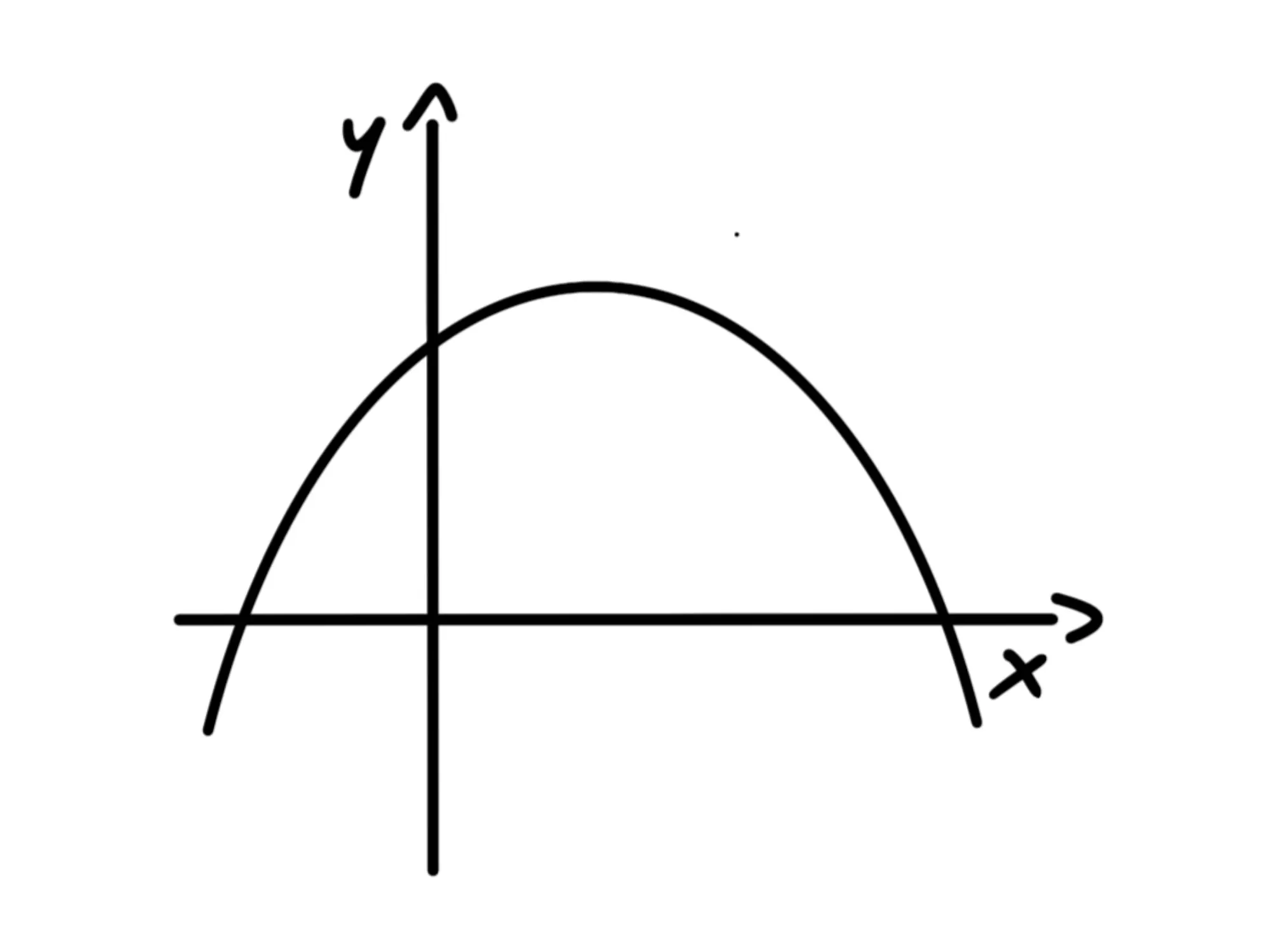
e notiamo che la $\displaystyle { x }$ del vertice è, per simmetria, il punto medio del segmento delimitato dalle due soluzioni.

Per calcolare il punto medio, trattandosi di un segmento orizzontale, ci basta fare la media dei due estremi, che sarebbero le due soluzioni.

Quest'ultime sono:

$\displaystyle { x_1 = {- b +\sqrt{\Delta}\over 2a} }$

$\displaystyle { x_2 = {-b-\sqrt{\Delta}\over 2a} }$

Quindi la loro media sarà uguale a:

$\displaystyle { {x_1 + x_2 \over 2} = {{-b + \sqrt{\Delta} \over 2a} + {-b - \sqrt{\Delta}2a}\over 2} }$ $\displaystyle { = {-b+ \sqrt{\Delta} - b - \sqrt{\Delta}\over 4a}= {-2b\over 4a}= -{b\over 2a} }$

Alternativamente potevamo direttamente ricordarci la formula per calcolare la somma delle soluzioni ed ottenere:

$\displaystyle { {x_1 + x_2 \over 2} = {{-b\over a} \over 2} = - {b\over 2a} }$

Fatto sta che la $\displaystyle { x }$ del vertice $\displaystyle { V_x }$ sarà uguale a $\displaystyle { {-b\over 2a}. }$

Per ottenere la $\displaystyle { y }$ ?

Il vertice appartiene alla parabola, quindi ci basta sostituire la sua $\displaystyle { x }$ nell'equazione per ottenere la sua $\displaystyle { y: }$

$\displaystyle { V_y = a\left( -{b\over 2a}\right)^2 +b \left(-{b\over 2a}\right) + c }$

$\displaystyle { V_y= {b^2 \over 4a} - {b^2 \over 2a} + c }$

Mettiamo tutto allo stesso denominatore:

$\displaystyle { V_y = {b^2 - 2 b^2 + 4ac \over 4a} }$

$\displaystyle { V_y = {-b^2 + 4ac \over 4a} }$

Ricordandoci che il $\displaystyle { \Delta }$ (Delta) è uguale a $\displaystyle { b^2 - 4ac, }$ possiamo riscriverla come:

$\displaystyle { V_y = -{\Delta \over 4a} }$

Quindi il vertice avrà coordinate $\displaystyle { (-{b\over 2a}; -{\Delta \over 4a}). }$

La formula per la $\displaystyle { y }$ del vertice già è più complicata e meno importante, ma la formula per $\displaystyle { V_x }$ è molto semplice e va assolutamente imparata perché la userete moltissime volte.

Avrete però notato che avevamo supposto che la parabola avesse due intersezioni con l'asse delle $\displaystyle { x. }$ E se non ce l'avesse?

Potrebbe benissimo essere così:

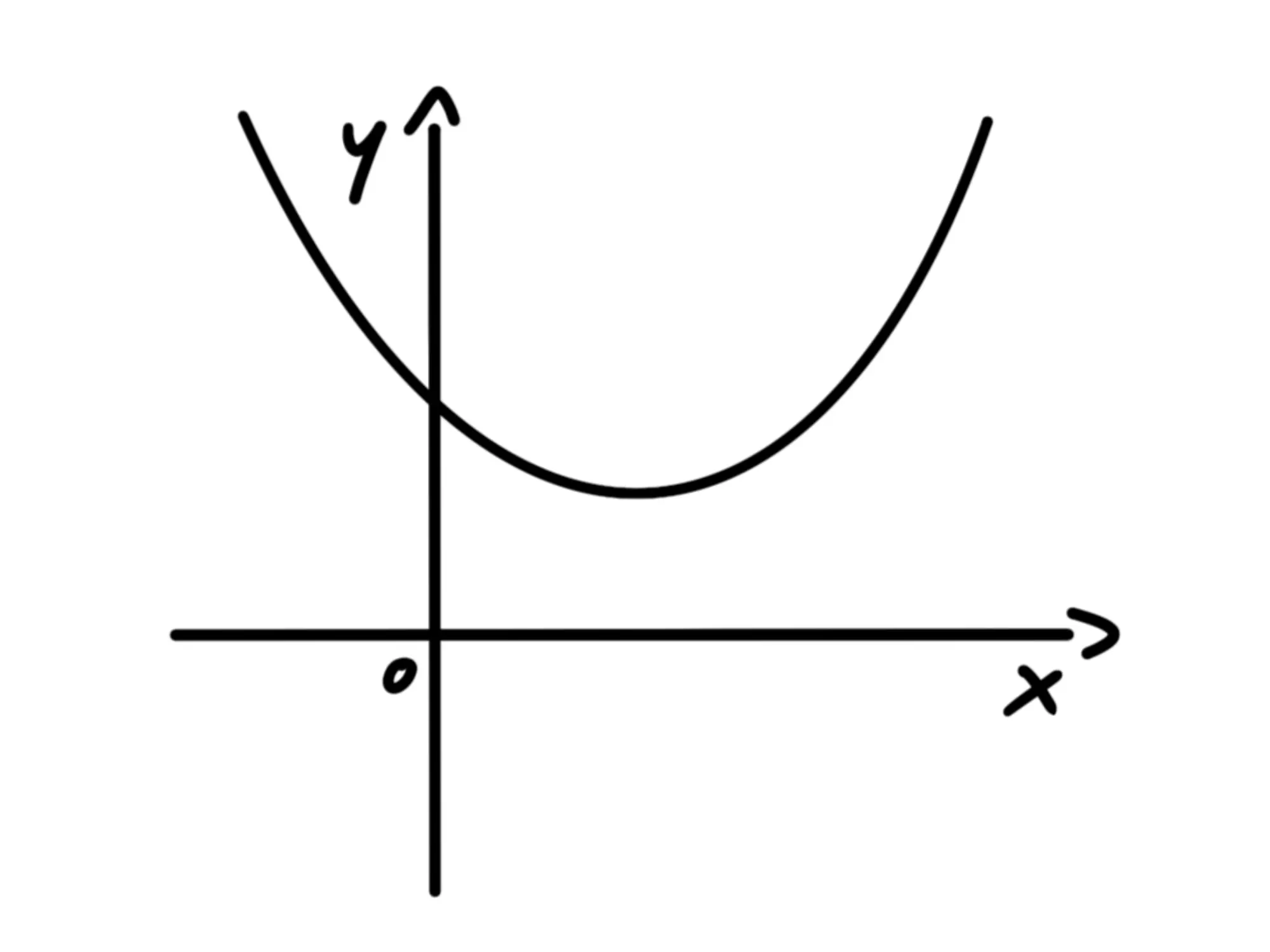
Notiamo che abbassare o alzare la parabola verticalmente non cambia la $\displaystyle { x }$ del vertice.

Possiamo quindi abbassare o alzare la parabola quanto ci serve affinché ci siano due soluzioni.

Matematicamente, abbassare o alzare la parabola equivale a sottrarre o aggiungere una costante all'equazione della parabola.

Se quindi l'equazione della parabola originaria era $\displaystyle { y = ax^2 + bx + c, }$ quella nuova sarà $\displaystyle { y=ax^2 +bx +c + k. }$

Prima abbiamo visto che i termini senza $\displaystyle { x }$ si semplificano, quindi come prima $\displaystyle { c }$ non influiva sulla $\displaystyle { x }$ del vertice, anche qui $\displaystyle { c+k }$ non influirà.

Se infatti facciamo i calcoli, otteniamo di nuovo che il $\displaystyle { \Delta }$ si semplifica e che $\displaystyle { V_x }$ vale $\displaystyle { -{b\over 2a}. }$

Quindi il vertice di questa nuova parabola traslata è sempre uguale a $\displaystyle { -{b\over 2a} }$ e quindi, siccome abbiamo detto che rimaneva uguale, anche la $\displaystyle { x }$ del vertice della parabola iniziale che non toccava l'asse delle $\displaystyle { x }$ sarà uguale a $\displaystyle { -{b\over 2a}. }$

Poi ci basta sostituirla nell'equazione per ottenere che $\displaystyle { V_y = -{\Delta \over 4a}. }$

Come abbiamo visto, però, questa dimostrazione è molto lunga. Quindi ora ne proponiamo un'altra più complicata ma anche molto più breve.

L'equazione della parabola è $\displaystyle { y=ax^2 + bx +c, }$ ma ricordiamoci che questa è in realtà l'equazione $\displaystyle { y={1\over 2(y_f -k)}x^2 - {x_f\over y_f -k}x + {x_f^2 + y_2^2 - k^2\over 2(y_f-k)} }$ con i nomi delle costanti cambiate.

Per definizione, la $\displaystyle { x }$ del vertice deve essere uguale alla $\displaystyle { x }$ del fuoco, cioè a $\displaystyle { x_f. }$

Notiamo che compare nel coeficciente del termine di primo grado, quello che sarebbe $\displaystyle { b. }$

Viene però divisa per $\displaystyle { y_f - k. }$ Ma questo stesso fattore compare nel coefficiente del termine di secondo grado, quello che sarebbe $\displaystyle { a. }$

Quindi se calcoliamo $\displaystyle { {b\over a} }$ otteniamo:

$\displaystyle { {-{x_f \over y_f - k}\over {1\over 2(y_f -k)}} = -{x_f \over y_f -k }\cdot {2(y_f - k)\over 1} = -2x_f }$

Se dunque dividiamo per $\displaystyle { -2 }$ otteniamo:

$\displaystyle { {{b\over a}\over -2} = {-2x_f \over -2} }$

$\displaystyle { -{b\over 2a} = x_f }$

ed avevamo appunto detto che $\displaystyle { V_x = x_f, }$ quindi $\displaystyle { V_x = -{b\over 2a}. }$

Questa dimostrazione è molto più veloce, però richiede di usare quella complicata forma dell'equazione della parabola, per questo solitamente si preferisce usare l'altra a scuola.

Ricordatevi quella che vi piace di più e che vi sembra più comoda.

Oltre che per il vertice, anche per il fuoco e per la direttrice esistono formule per calcolarne le coordinate.

La $\displaystyle { x }$ del fuoco, essendo uguale a quella vertice, sarà infatti uguale a $\displaystyle { -{b\over 2a}. }$

Si può poi dimostrare che la sua $\displaystyle { y }$ deve essere uguale a $\displaystyle { {1-\Delta \over 4a}. }$

Dal fatto che il vertice deve stare a metà strada tra il fuoco e la direttrice, si ottiene che l'equazione della direttrice deve essere uguale a:

$\displaystyle { d = - {1 + \Delta \over 4a} }$

Parabola con asse parallelo all'asse x

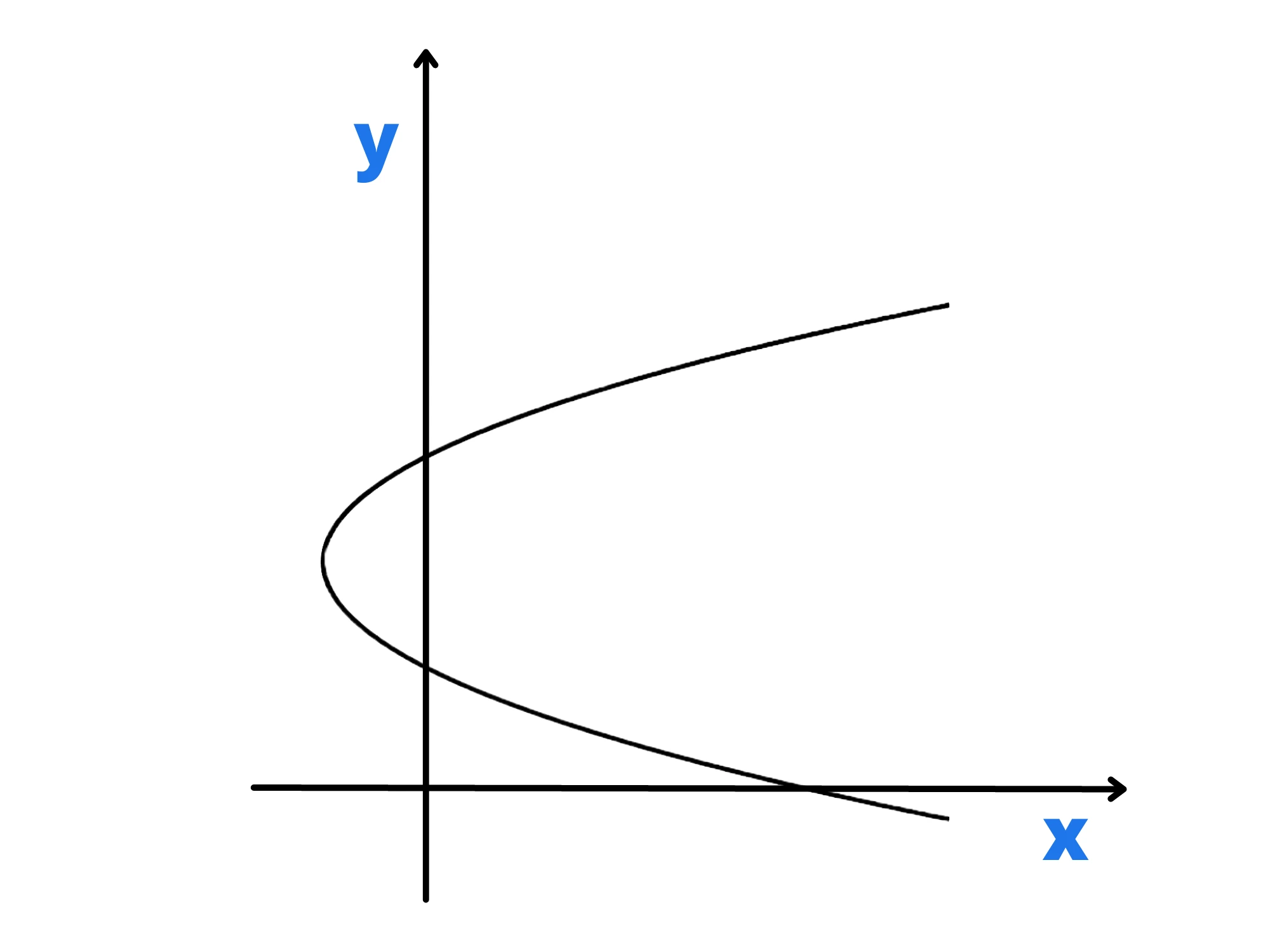
Le parabole di questo tipo hanno equazione

n questo caso il parametro $\displaystyle { a }$ ci indica se la parabola è rivolta verso sinistra $\displaystyle { (a > 0) }$ o se è rivolta verso destra $\displaystyle { (a < 0) }$ . In generale, le sue caratteristiche sono molto simili a quelle delle parabole studiate in precedenza. Per questo citiamo solo le formule che ci interessano:

Coordinate del vertice $\displaystyle { V \bigg( -\frac{\Delta}{4a}, -\frac{b}{2a}\bigg) }$

Coordinate del fuoco $\displaystyle { F \bigg( \frac{1-\Delta}{4a}, \frac{-b}{2a} \bigg) }$

Ricordatevi infine che una parabola con asse parallelo all'asse delle $x$ non è mai una funzione, perché ad una $\displaystyle { x }$ corrispondono più $\displaystyle { y. }$