Rette

Rette particolari

Analizziamo, come prima cosa, il caso di una retta parallela all'asse delle $\displaystyle { x }$.

Prendiamo una qualsiasi retta di questo tipo e chiamiamo con $\displaystyle { k }$ il punto di intersezione della retta con l'asse delle $\displaystyle { y }$.

Siccome questa retta è orizzontale, notiamo che tutti i suoi punti hanno la stessa ordinata (la stessa $\displaystyle { y }$ ) e che quindi hanno coordinate $\displaystyle { P(x_P, k) }$, con $\displaystyle { x_P }$ variabile e $\displaystyle { k }$ costante.

Quindi la condizione affinché un punto appartenga alla retta è che la sua $\displaystyle { y }$ sia uguale a $\displaystyle { k. }$

Per questo possiamo dire che l'equazione di una generica retta parallela all'asse delle ascisse è

in quanto è l'insieme di tutti e soli i punti che hanno ordinata $\displaystyle { k }$ (e ascissa variabile).

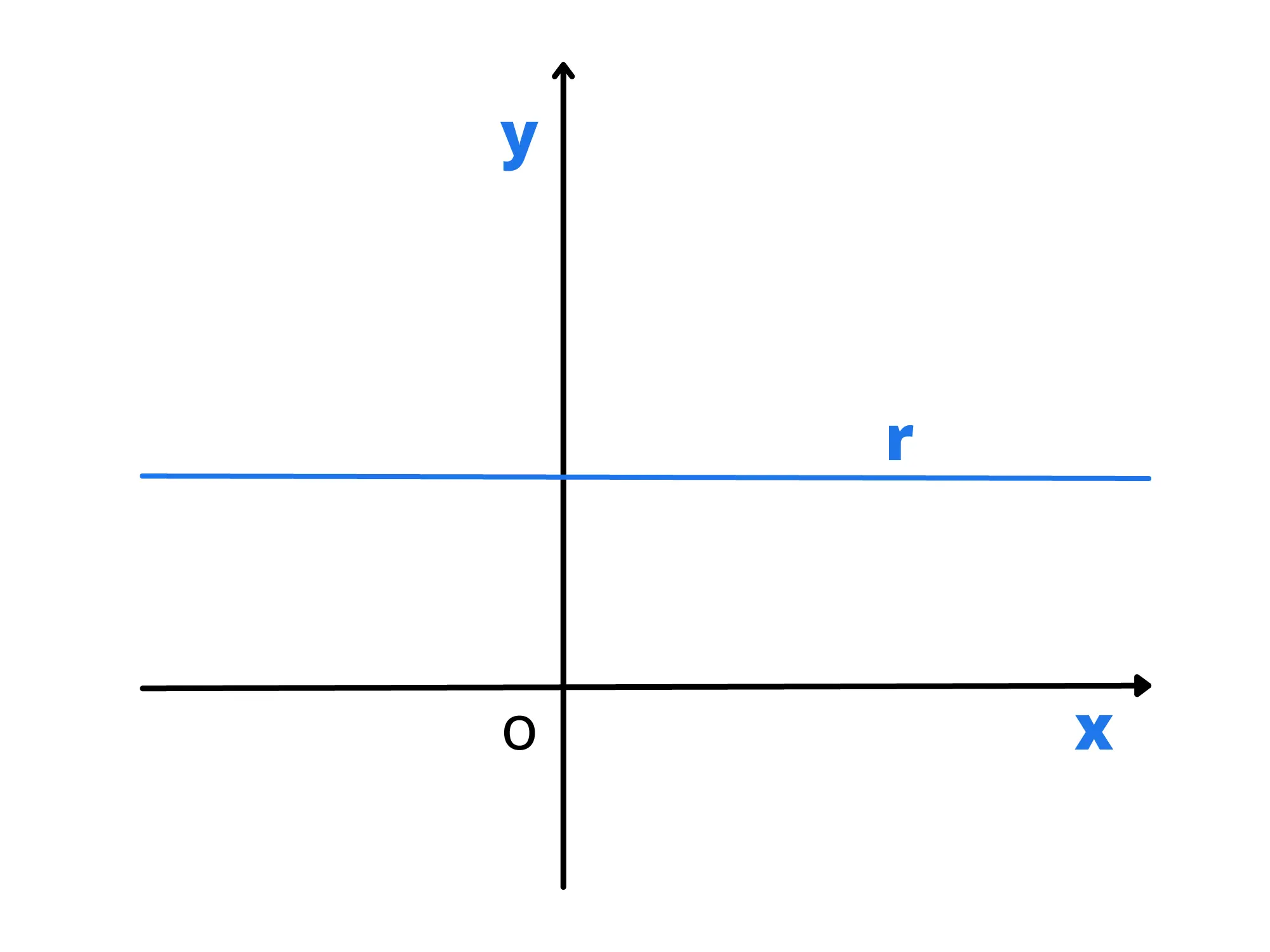
Notiamo infine che se $\displaystyle { k=0 }$ la retta che otteniamo coincide con quella dell'asse $\displaystyle { x }$ che quindi ha equazione

Analogamente possiamo procedere per ricavare la formula generale delle rette parallele all'asse delle $\displaystyle { y }$ .

Prendiamo anche in questo caso una retta di questo tipo e chiamiamo con $\displaystyle { h }$ il punto di intersezione della retta con l'asse delle $\displaystyle { x }$ .

Notiamo che tutti i punti della retta hanno la stessa ascissa e che quindi hanno coordinate $\displaystyle { P(h, y_P) }$ , con $\displaystyle { h }$ costante e $\displaystyle { y_P }$ variabile. Per questo possiamo dire che l'equazione generica di una retta parallela all'asse $\displaystyle { y }$ è

In quanto è l'insieme di tutti e soli i punti ascissa uguale a $\displaystyle { h }$ (e ordinata variabile).

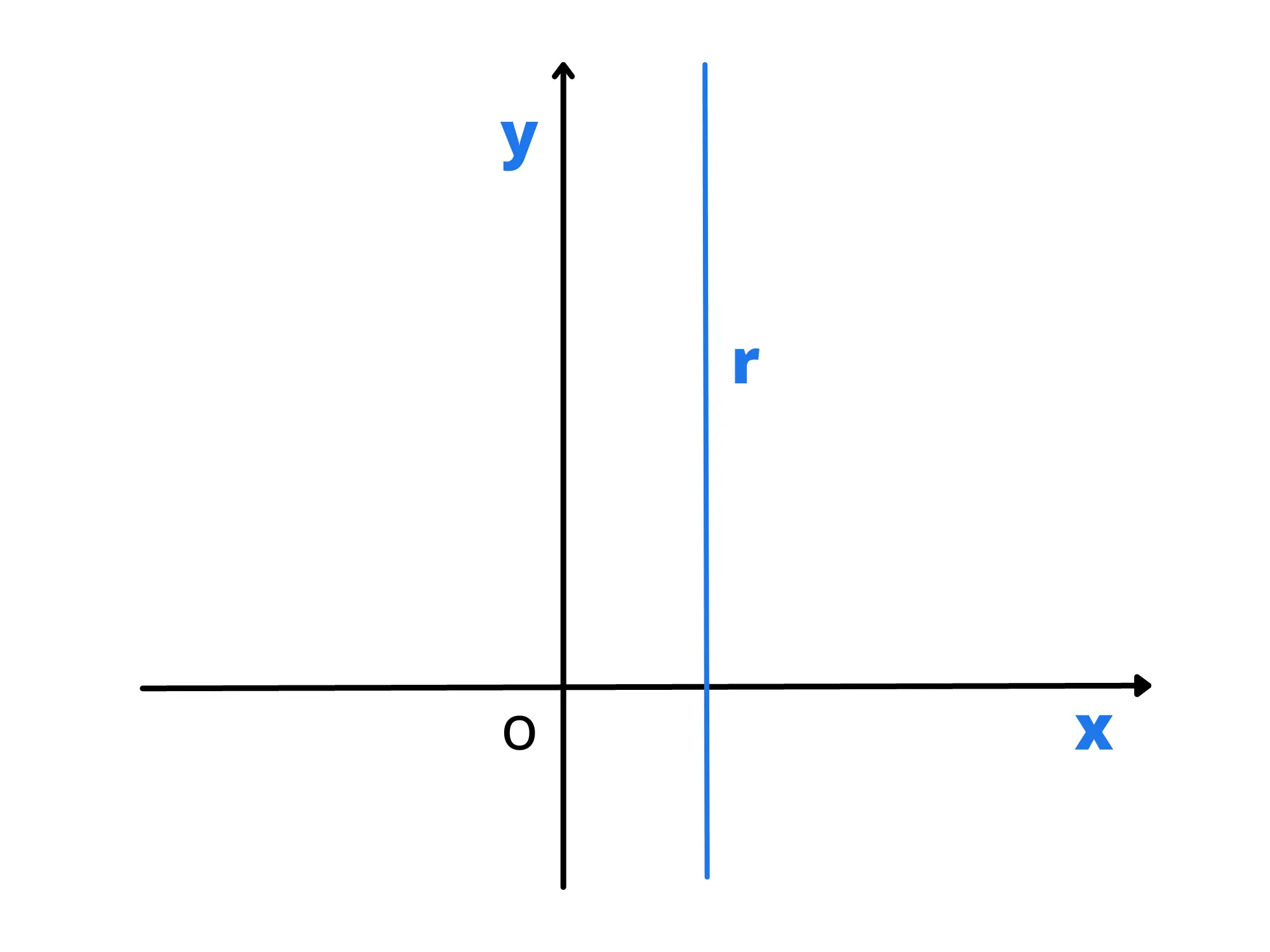
Notiamo infine che se $\displaystyle { h=0 }$ la retta che otteniamo coincide con quella dell'asse $\displaystyle { y }$ che quindi ha equazione

$\displaystyle { x=0 }$

Prendiamo una retta che passa per l'origine:

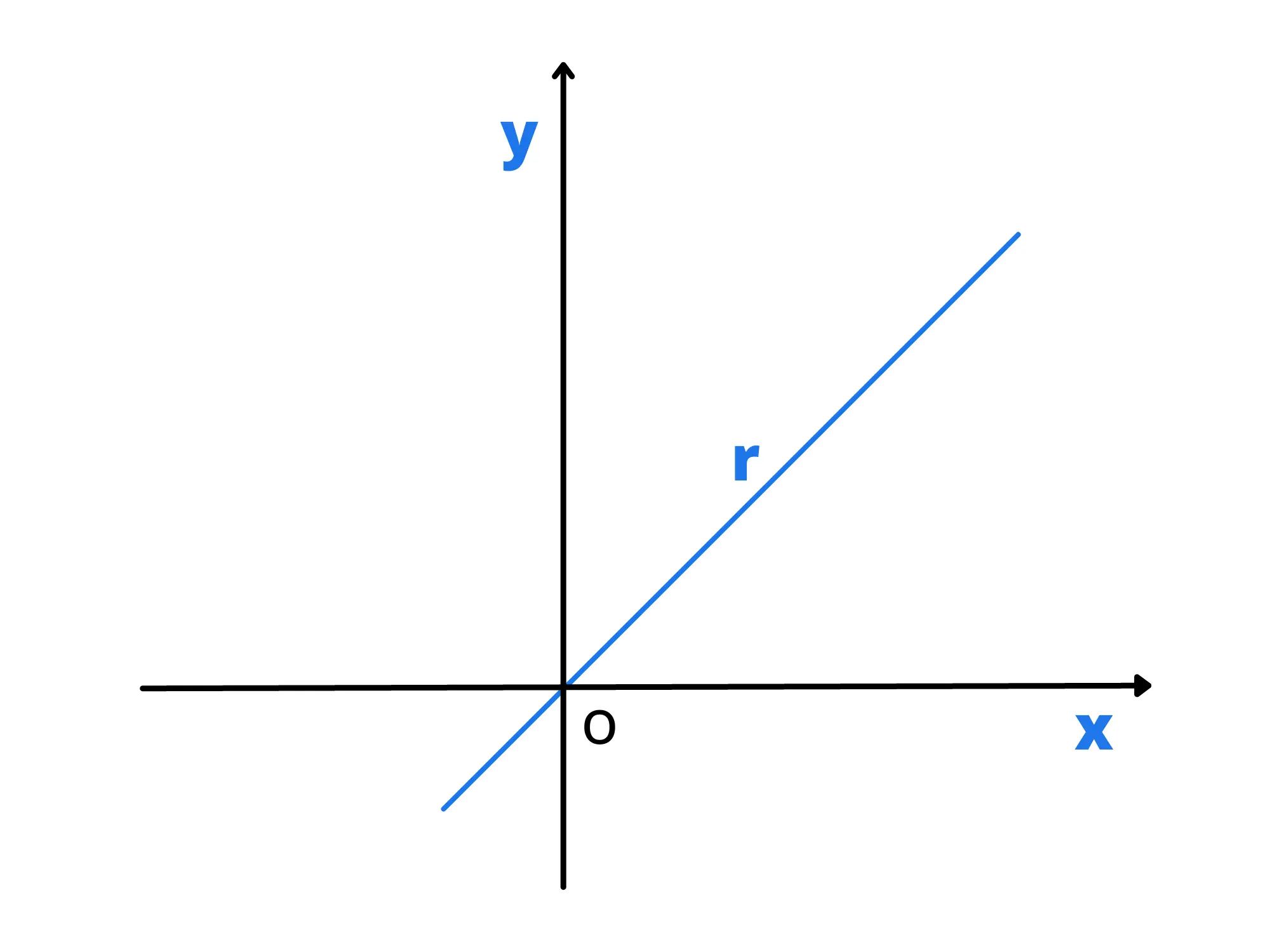
La sua equazione è del tipo $\displaystyle { y = mx, }$ dove $\displaystyle { m }$ è una costante a cui diamo il nome di coefficiente angolare .

Questo significa che le ascisse e le ordinate dei punti di una retta passante per l'origine sono direttamente proporzionali.

Quindi, facendo variare $\displaystyle { m, }$ otterremo tutte le rette passanti per l'origine.

Per convincerci della veridicità di quest'equazione, proviamo a rappresentare l'equazione $\displaystyle { y=3x }$ sul piano cartesiano. Per farlo compiliamo una tabella con i valori di $\displaystyle { x }$ e $\displaystyle { y }$ :

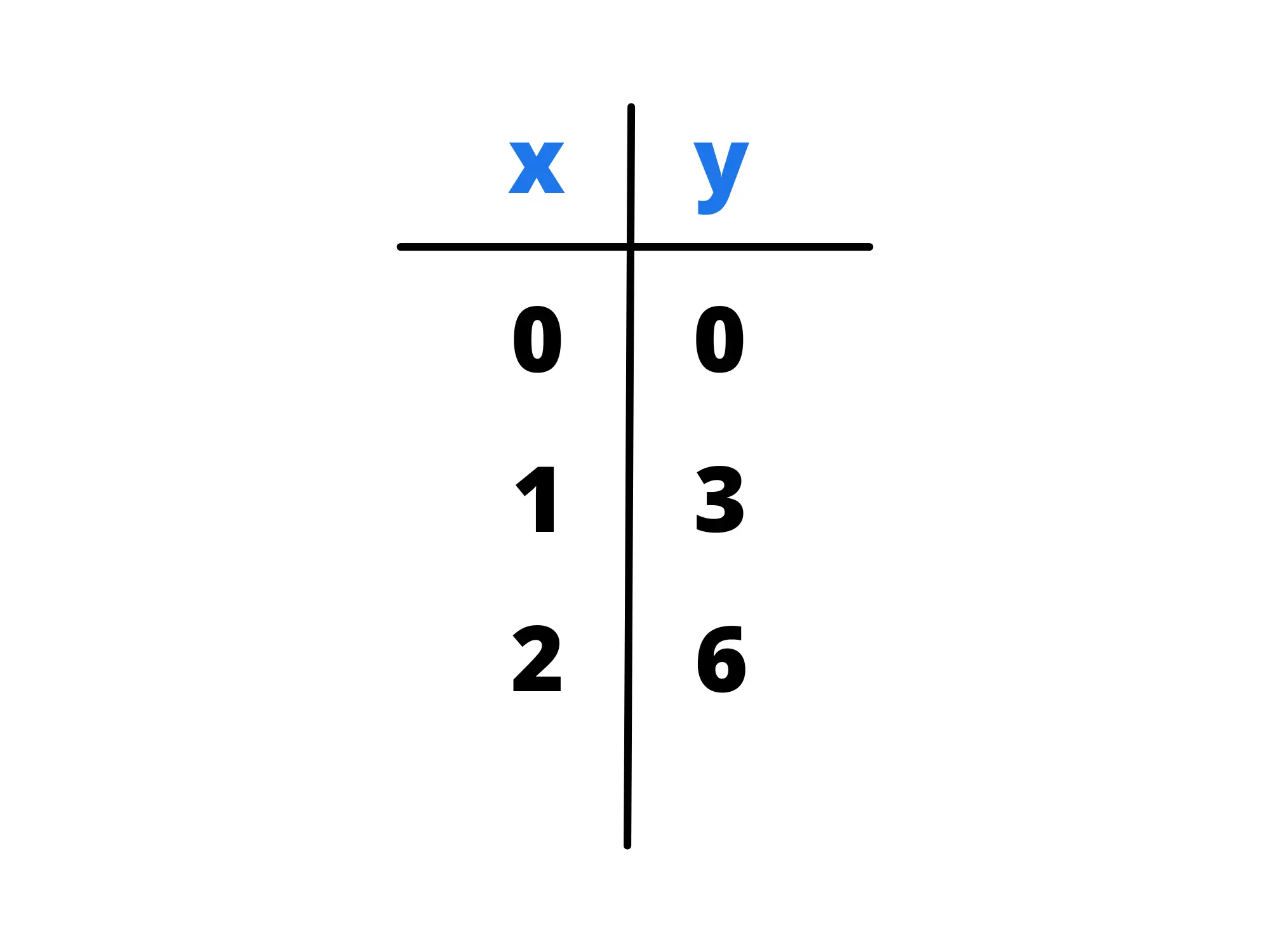
Disegniamo quei punti sul piano cartesiano e tracciamo la retta passante per essi.

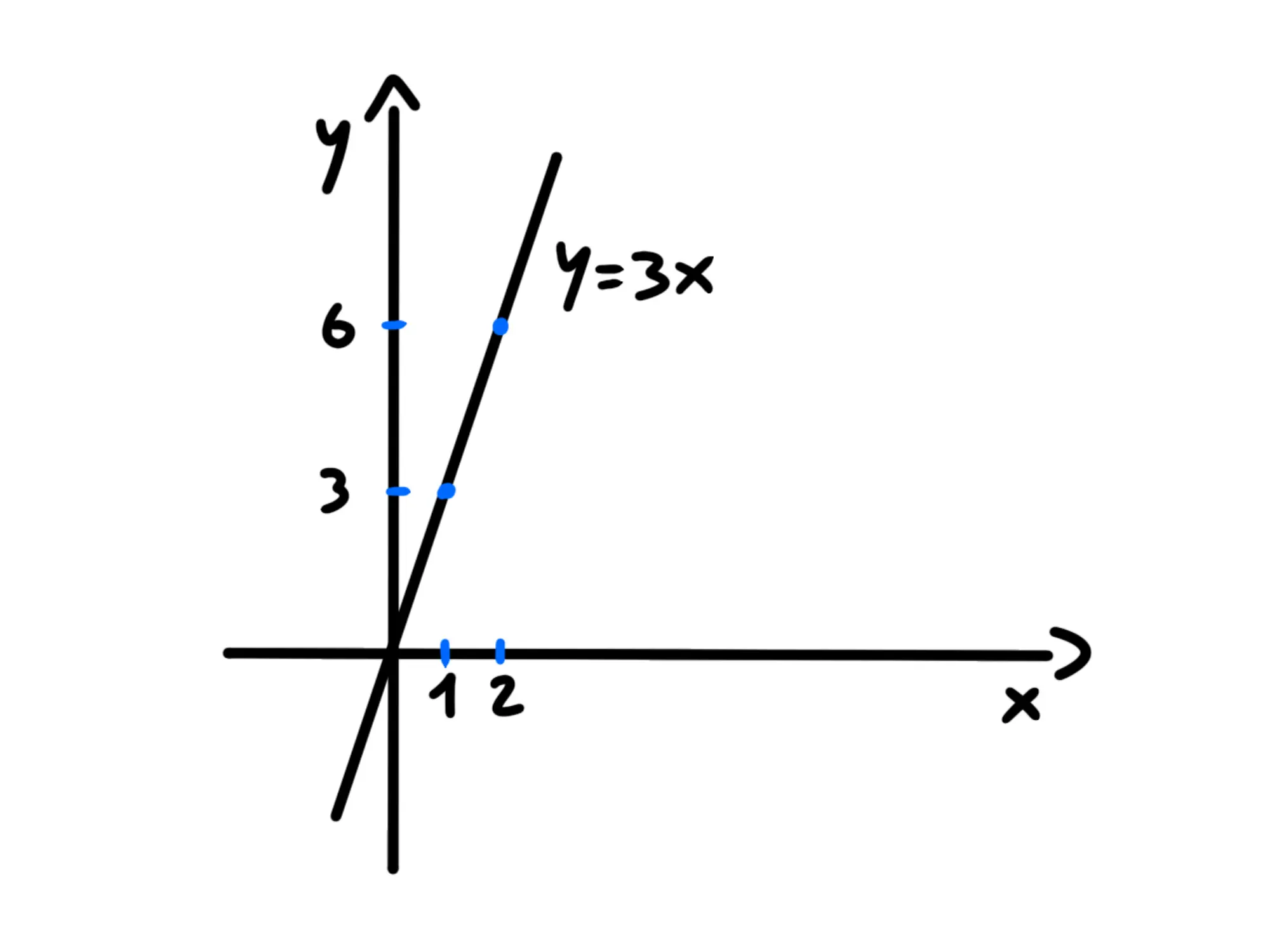
Tutti i punti che potete trovare che rispettano l'equazione $\displaystyle { y=3x }$ si troveranno proprio sopra questa retta.

Notiamo che se $\displaystyle { m }$ è positivo, mettendo una $\displaystyle { x }$ positiva otteniamo una $\displaystyle { y }$ positiva, mentre mettendone una negativa otteniamo una $\displaystyle { y }$ negativa.

Quindi significa che tutti i punti delle rette con $\displaystyle { m }$ positivi hanno o ascissa e ordinata positiva, oppure sono entrambe negative.

Ciò significa che la retta giace nel prima e nel terzo quadrante.

Se invece $\displaystyle { m }$ è negativo, otteniamo il contrario. Cioè quando le $\displaystyle { x }$ sono positive le $\displaystyle { y }$ sono negative e quando le $\displaystyle { x }$ sono negative le $\displaystyle { y }$ sono positive.

Quindi le rette con $\displaystyle { m }$ negative giacciono nel secondo e quarto quadrante:

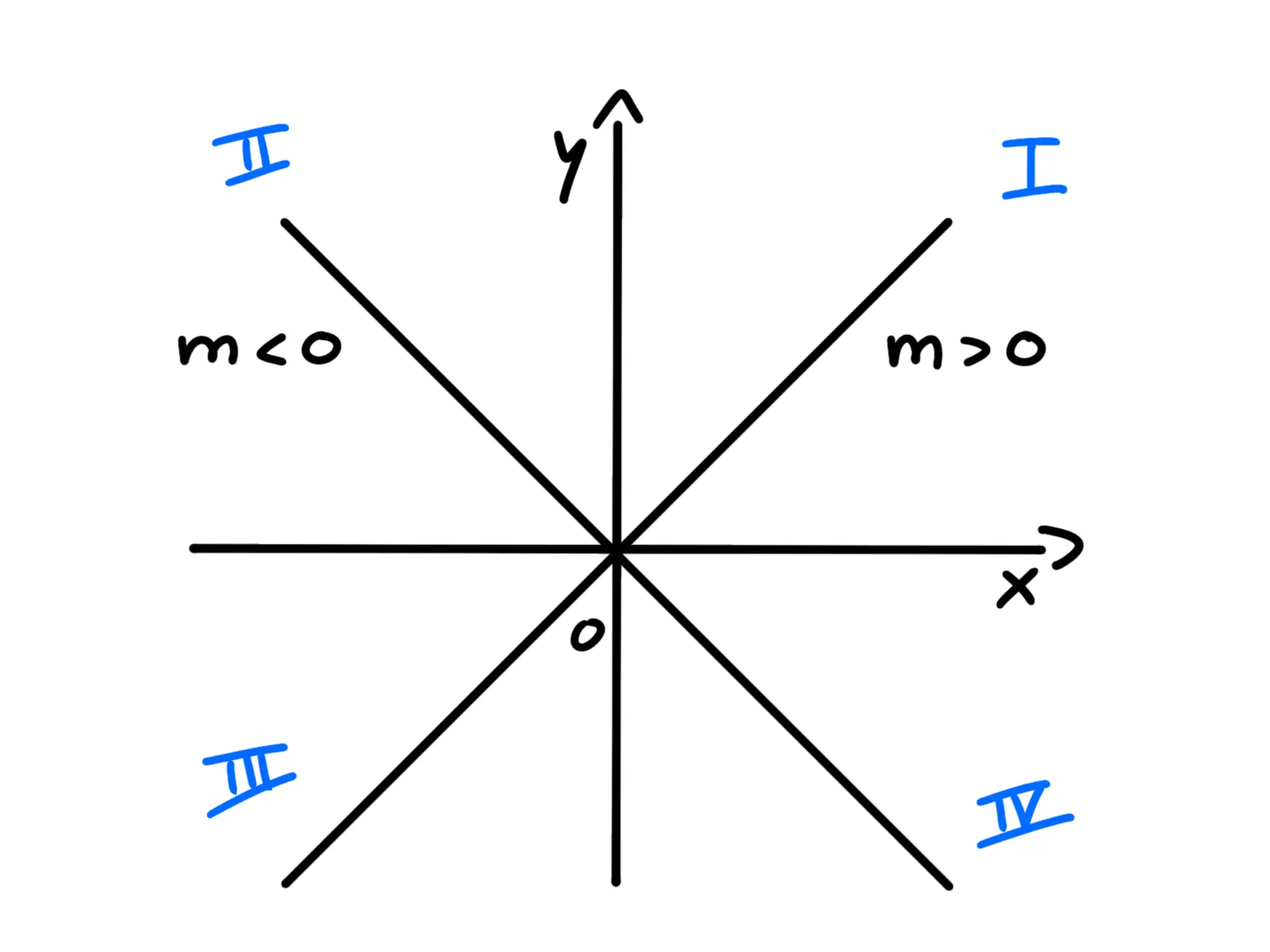
In generale, il coefficiente angolare ci dice quanto è inclinata la retta rispetto all'asse delle $\displaystyle { x. }$

Retta generica non parallela all'asse delle y

Una retta non deve passare per l'origine, ma può stare più in alto o più in basso:

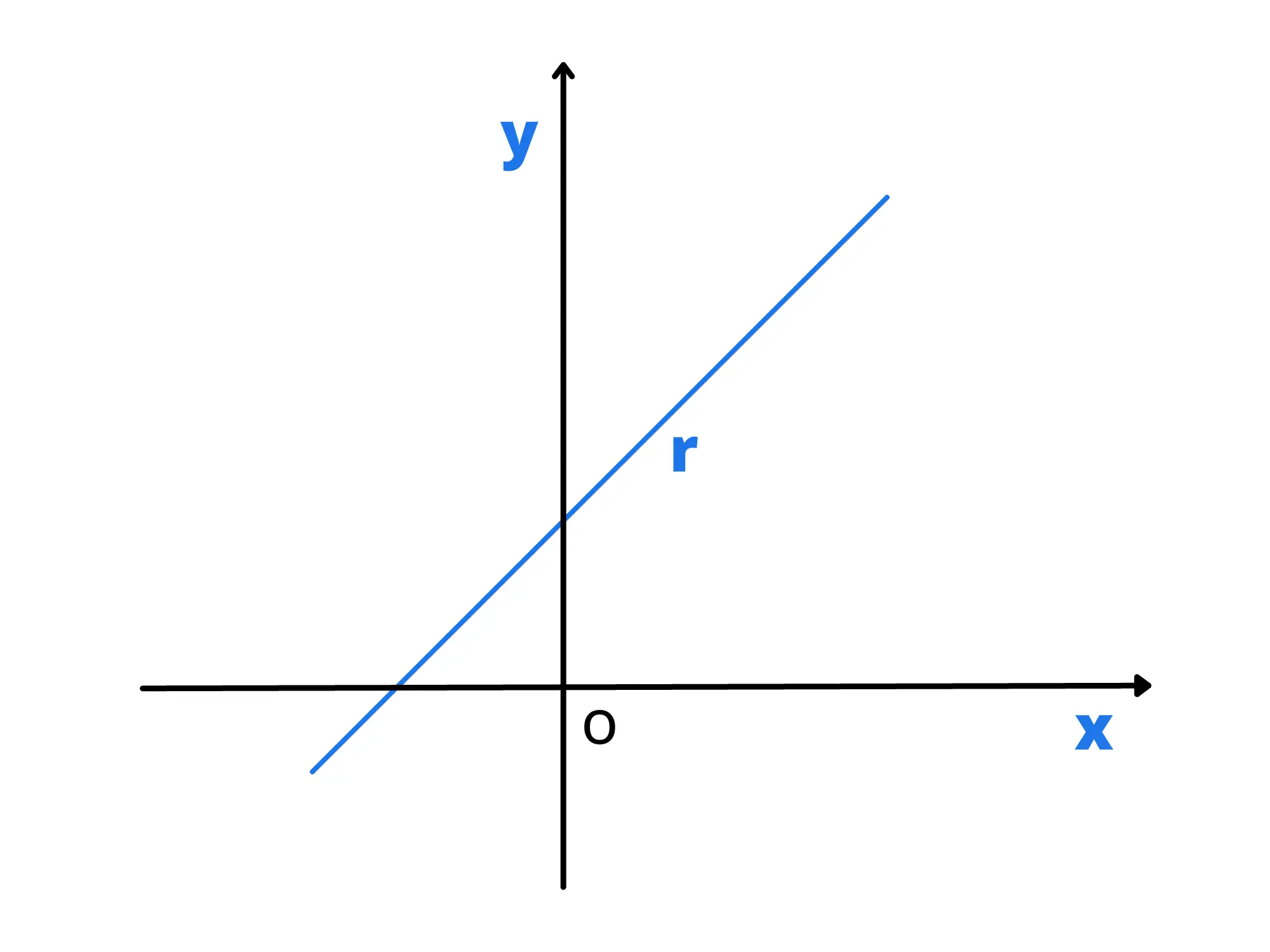
Quindi se abbiamo alzato o abbassato la retta, significa che abbiamo sommato o sottratto una costante a tutte le $\displaystyle { y }$ dei punti della retta.

Quindi l'equazione da $\displaystyle { y=mx }$ diventa $\displaystyle { y=mx +q. }$ Questo $\displaystyle { q }$ viene solitamente chiamato intercetta all'origine.

Perché? Perché se mettiamo $\displaystyle { x=0, }$ otteniamo $\displaystyle { y=q, }$ quindi $\displaystyle { q }$ è l'altezza a cui la retta incontra l'asse $\displaystyle { y. }$

Infatti se mettiamo $\displaystyle { q=0 }$ otteniamo il caso di prima e la retta taglia l'asse $\displaystyle { y }$ nell'origine.

Notiamo che se mettiamo $\displaystyle { m=0 }$ otteniamo $\displaystyle { y=q, }$ che era l'equazione delle rette parallele all'asse $\displaystyle { x }$ (quelle orizzontali).

E quando otteniamo quelle invece parallele all'asse $\displaystyle { y }$ (quelle verticali)? In questa forma qua, non le otteniamo mai, perché non possiamo far scomparire la $\displaystyle { y. }$

Quella che infatti abbiamo visto è l'equazione della retta in forma esplicita . Si chiama così perché la $\displaystyle { y }$ è isolata, cioè è esplicita.

Esiste infatti anche la forma implicita della retta che ci permettere di esprimere anche le rette parallele all'asse $\displaystyle { y, }$ che vedremo nel prossimo capitolo.

Forma implicita dell'equazione della retta

In generale, oltre alla $\displaystyle { x }$ , possiamo aggiungere un coefficiente anche alla $\displaystyle { y. }$

In questo modo, quando metteremo questo coefficiente uguale a $\displaystyle { 0, }$ otterremo l'equazione delle rette parallele all'asse $\displaystyle { y. }$

Questa volta però portiamo tutti i termini a sinistra dell'uguale, quindi l'equazione implicita della retta sarà:

$\displaystyle { ax + by + c =0 }$

Perché questa volta il coefficiente della $\displaystyle { x }$ si chiama $\displaystyle { a }$ e non più $\displaystyle { m? }$

Perché non è più il coefficiente angolare. Otteniamo il coefficiente angolare quando isoliamo la $\displaystyle { y. }$ Se infatti la isoliamo otteniamo:

$\displaystyle { y = -{a\over b}x - {c \over b} }$

E quindi il coefficiente angolare sarebbe uguale a $\displaystyle { -{a\over b}, }$ non ad $\displaystyle { a, }$ per questo ora il suo coefficiente ha un nome diverso.

Quindi l'equazione in forma implicita della retta può descrivere tutte le rette del piano cartesiano.

Quindi, anche se l'equazione in forma esplicita è più comoda, a volte si preferisce usare quella implicita perché è più generale.

Come passare da una forma all'altra?

Se hai l'equazione in forma implicita, ti basta isolare la $\displaystyle { y }$ per ottenerla in forma esplicita.

Se hai la forma esplicita è ancora più facile, perché ti basterà portare tutto a sinistra dell'uguale ed otterrai la forma implicita.

Vediamo un paio di esempi:

Se hai $\displaystyle { - 4x +2y +1=0, }$ per ottenere la forma esplicita ti basta isolare la $\displaystyle { y: }$

$\displaystyle { 2y = 4x -1 }$

$\displaystyle { y = 2x - {1\over 2} }$

Se invece hai $\displaystyle { y= 3x -1, }$ per ottenere la forma implicita ti basta portare tutto a sinistra dell'uguale:

$\displaystyle { y - 3x +1 =0 }$

$\displaystyle { -3x + y +1 =0 }$

Retta passante per due punti

Un noto postulato della geometria afferma che per due punti passa una sola retta. Supponendo vero questo, se abbiamo due punti, ci sarà una sola retta che passa per essi e quindi ci dovrà essere un modo per risalire alla sua equazione.

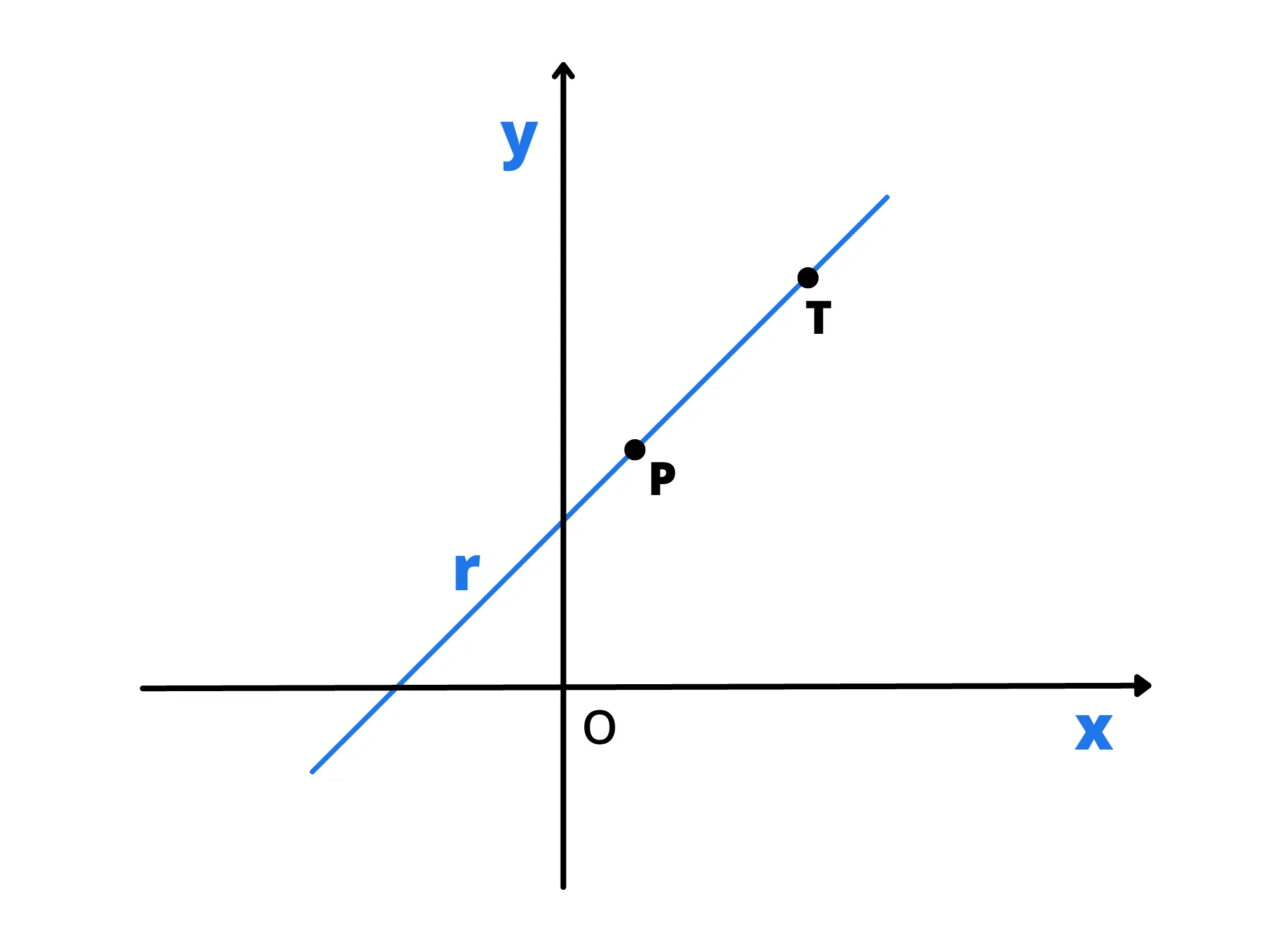
Supponiamo dunque di avere due punti $\displaystyle { P(x_P,y_P) }$ e $\displaystyle { T(x_T,y_T) }$ , sapendo che appartengono alla retta, devono verificare la sua equazione. Quindi:

$\displaystyle { \left\{ \begin{array}{l} y_P = mx_P+q\\ y_T =mx_T+q\end{array} \right. }$

Notiamo che il coefficiente angolare e il termine noto sono uguali in quanto stiamo parlando della stessa retta. Infatti $\displaystyle { m }$ e $\displaystyle { q }$ sono le uniche incognite del sistema in quanto gli altri sono coefficienti e corrispondono alle coordinate dei due punti, che noi abbiamo.

Se sottraiamo la seconda equazione alla prima la variabile scompare e dunque otteniamo:

$\displaystyle { y_P - y_T = mx_P - mx_T }$

L'unica incognita che abbiamo è il coefficiente angolare, e quindi ci basta isolarlo per trovare una formula più pulita

$\displaystyle { m ={y_P - y_T \over x_P- x_T} }$

Questa è la formula che ci permette di trovare il coefficiente angolare di una retta partendo da due suoi punti. Molto spesso, vista la sua importanza, si richiede di impararla a memoria.

Questa si tratta di una formula molto importante e ci dice che il coefficiente angolare è uguale alla differenza, cioè alla variazione, delle $\displaystyle { y }$ fratto la variazione delle $\displaystyle { x. }$

Spesso utilizziamo il $\displaystyle { \Delta }$ per indicare il concetto di differenza. Per questo spesso richiamiamo $\displaystyle { y_P - y_T }$ come $\displaystyle { \Delta y }$ e $\displaystyle { x_P - x_T }$ come $\displaystyle { \Delta x. }$

$\displaystyle { m = {\Delta y \over \Delta x} }$

Adesso non ci serve altro che trovare una formula per $\displaystyle { q }$ . Per farlo basta sostituire $\displaystyle { m }$ in una delle $\displaystyle { 2 }$ equazioni del sistema:

$\displaystyle { y_P = {(y_P-y_T) \cdot x_P \over (x_P-x_T)} + q }$

Quindi portando tutto dallo stesso lato ed allo stesso denominatore:

$\displaystyle { q= {y_P(x_P - x_T) - x_P(y_P-y_T) \over x_P -x_T} }$

$\displaystyle { q = {x_Py_T - y_Px_T \over x_P-x_T} }$

Come si può notare è una formula abbastanza complicata da ricoradare. Di solito si evita di impararla a memoria e si decide di studiare solo quella per trovare $\displaystyle { m }$ . Infatti, una volta che si conosce $\displaystyle { m }$ si può sostituire direttamente il suo valore numerico nell'equazione precedente

$\displaystyle { y_P = mx_P + q \longrightarrow q = y_P - mx_P }$

per trovare il valore numerico di $\displaystyle { q }$

La formula di $\displaystyle { q }$ però è interessante perché, risostituendola nell'equazione di una retta, ci permette di trovare una formula diretta per l'equazione della retta passsane per i due punti.

Sostituendo $\displaystyle { m }$ e $\displaystyle { q }$ nell'equazione generale di una retta scritta in forma esplicita infatti otteniamo:

$\displaystyle { y = mx + q }$

$\displaystyle { y = {y_P - y_T \over x_P - x_T}x + {x_Py_T - y_Px_T \over x_P - x_T} }$

Si tratta di un'equazione piuttosto complicata, quindi proviamo a semplificarla con qualche passaggio algebrico:

Portiamo tutto allo stesso denominatore:

$\displaystyle { y = {(y_P - y_T)x + x_Py_T - y_Px_T \over x_P - x_T} }$

Ora sottraiamo $\displaystyle { y_P }$ da entrambi i lati:

$\displaystyle { y-y_P ={(y_P - y_T)x + x_Py_T - y_Px_T \over x_P - x_T}-y_P }$

$\displaystyle { y-y_P = {(y_P - y_T)x + x_Py_T - y_Px_T -y_Px_P +y_Px_T \over x_P - x_T} }$

Semplifichiamo e raccogliamo:

$\displaystyle { y-y_P = {(y_P - y_T)x + x_Py_T - y_Px_P \over x_p - x_T} }$

$\displaystyle { y-y_P = {(y_P - y_T)x - (y_P - y_T)x_P \over x_p - x_T} }$

$\displaystyle { y-y_P = {(y_P - y_T)(x-x_P) \over x_p - x_T} }$

Ora dividiamo entrambi i lati per $\displaystyle { y_P-y_T: }$

$\displaystyle { {y-y_P\over y_P - y_T} = {x - x_P \over x_p - x_T} }$

Ed infine moltiplichiamo entrambi i lati per $\displaystyle { -1 }$ per cambiare il segno delle differenze:

$\displaystyle { {y-y_P\over y_T - y_P} = {x - x_P \over x_T - x_P} }$

In questo modo c'è una certa simmetria nella formula e questo ci aiuta a ricordarcela.

Può essere molto utile come formula perché ci permette di trovare subito l'equazione della retta, però può essere difficile ricordarsela, quindi se ve la dimenticate potete anche solo trovare il coefficiente angolare con la semplice formula $\displaystyle { m = {\Delta y \over \Delta x}, }$ sostituirlo in una delle due equazioni per trovare $\displaystyle { q }$ ed infine sostituire entrambi nell'equazione generica della retta in forma esplicita.

Posizione reciproca tra due rette

Due rette $\displaystyle { r }$ e $\displaystyle { t }$ possono essere incidenti, parallele e distinte o coincidenti. Nelle prossime sezioni analizzeremo approfonditamente ogni caso.

Geoemetricamente, due rette si dicono incidenti se si incotrano in uno stesso punto che viene chiamato punto di intersezione. Per capire se le due rette sono incidenti bisogna analizzare il loro coefficiente angolare: se è diverso le rette avranno inclinazione diversa e quindi si incontreranno in un punto.

Per trovare il punto di intersezione partendo dalle due equazioni dobbiamo fare un sistema tra le due rette e porre uguale in entrambe le equazioni la $\displaystyle { x }$ e la $\displaystyle { y }$ . Facendo ciò otteremo un sistema a due incognite facilmente risolvibile

$\displaystyle { \left\{ \begin{array}{l} y = m_1 x + q_1 \\ y = m_2 x + q_2 \end{array} \right. }$

Esempio: Date le due rette $\displaystyle { 2x+y-2=0 }$ e $\displaystyle { 3x-y-3=0 }$ verificare che esse siano incidenti e trovare il loro punto di intersezione

Per prima cosa dobbiamo verificare che esse siano incidenti. Per farlo troviamo il coefficiente angolare di entrambe le rette esplicitandole:

$\displaystyle { 2x+y-2=0 \longrightarrow y= -2x+2 }$ quindi $\displaystyle { m_1=-2 }$

$\displaystyle { 3x-y-3=0 \longrightarrow y=3x-3 }$ quindi $\displaystyle { m_2=3 }$

Notiamo che le rette sono incidenti perché $\displaystyle { m_1 \neq m_2 }$ . Per trovare il loro punto di intersezione $\displaystyle { P }$ risolviamo il sistema formato dalle loro equazioni, ad esempio con il metodo del confronto:

$\displaystyle { \left\{ \begin{array}{l} 2x+y-2=0 \\ 3x-y-3=0 \end{array} \right. \longrightarrow }$ $\displaystyle { \left\{ \begin{array}{l} y=-2x+2 \\ y=3x-3 \end{array} \right. }$

$\displaystyle { \left\{ \begin{array}{l} -2x+2=3x-3 \\ y=3x-3 \end{array} \right. \longrightarrow }$ $\displaystyle { \left\{ \begin{array}{l} x=1 \\ y=0 \end{array} \right. }$

Quindi $\displaystyle { P(1,0) }$

Geoemetricamente, due rette si dicono parallele se non hanno alcun punto in comune. Per capire se due rette sono parallele bisogna analizzare il loro coefficiente angolare: se è identico significa che le rette hanno la stessa inclinazione e quindi che non si incontreranno mai.

Esempio: Date le due rette $\displaystyle { 4x-3y+2=0 }$ e $\displaystyle { 8x-6y+3=0 }$ , verificare che sono parallele.

Analizziamo per prima cosa il coefficiente angolare delle due rette ponendole in forma esplicita:

$\displaystyle { 4x-3y+2=0 }$ $\displaystyle { \longrightarrow y=\frac{4}{3}x+\frac{2}{3} }$

$\displaystyle { 8x-6y+3=0 }$ $\displaystyle { \longrightarrow y=\frac{4}{3}x+\frac{1}{2} }$

Notiamo che le due rette hanno lo stesso coefficiente angolare e che quindi sono parallele.

Un caso particolare di rette parallele è quello delle rette coincidenti. Infatti, se hanno sia lo stesso coefficiente angolare sia lo stesso termine noto, avremo due rette uguali. Rette di questo tipo hanno tutti gli infiniti punti in comune.

Esempio: Date le due rette $\displaystyle { x+3y-4=0 }$ e $\displaystyle { 2x+6y-8 }$ , verificare che esse siano coincidenti.

Anche in questo caso, analizziamo il coefficiente angolare e il termine noto di entrambe le equazioni: se sono uguali allora le rette saranno coincidenti:

$\displaystyle { x+3y-4=0 }$ $\displaystyle { \longrightarrow y=-\frac{1}{3}x+\frac{4}{3} }$

$\displaystyle { 2x+6y-8=0 }$ $\displaystyle { \longrightarrow y=-\frac{1}{3}x+\frac{4}{3} }$

Le rette hanno $\displaystyle { m_1=m_2 }$ e $\displaystyle { q_1=q_2 }$ e quindi sono uguali. Notiamo che potevamo arrivare alla stessa soluzione moltiplicando per $\displaystyle { 2 }$ entrambi i membri della prima equazione, ottenendo la seconda.

Retta come luogo geometrico

Possiamo vedere la retta anche come un luogo geometrico.

Iniziamo, come prima, iniziamo dalla retta passante per l'origine:

Ricordiamoci che la sua equazione era $\displaystyle { y = mx, }$ dalla quale otteniamo che $\displaystyle { m = {y\over x}, }$ cioè che il rapporto tra l'ordinata e l'ascissa del punto è costante.

Possiamo quindi definire la retta passante per l'origine come il luogo geometrico dei punti tali che il rapporto tra l'ordinata e l'ascissa è uguale ad una data costante.

Per il caso più generale è più difficile dare la sua definizione come luogo geometrico.

Infatti normalmente si definisce la retta generica come il luogo geometrico dei punti allineati in una stessa direzione in maniera continua.