La notazione scientifica è un metodo usato per scrivere più facilmente i numeri molto grandi o molto piccoli.
Come funziona? Iniziamo con un esempio molto semplice. Prendiamo il numero Possiamo riscriverlo come e cento è uguale a dieci alla seconda, dunque è uguale a
Se prendo posso riscriverlo come Come nel caso di prima, vogliamo riscrivere il secondo fattore come una potenza di Per capire qual'è l'esponente della potenza, dobbiamo contare i suoi zeri. Questo ne ha quindi possiamo riscrivere il nostro numero come
Vedete come è molto più breve? Come fare però per un numero che non ha tutti zeri, come In tal caso dobbiamo pensare di scrivere una virgola alla fine del numero e di spostarla verso sinistra fino ad incontrare l'ultimo numero, come si vede nel seguente grafico:
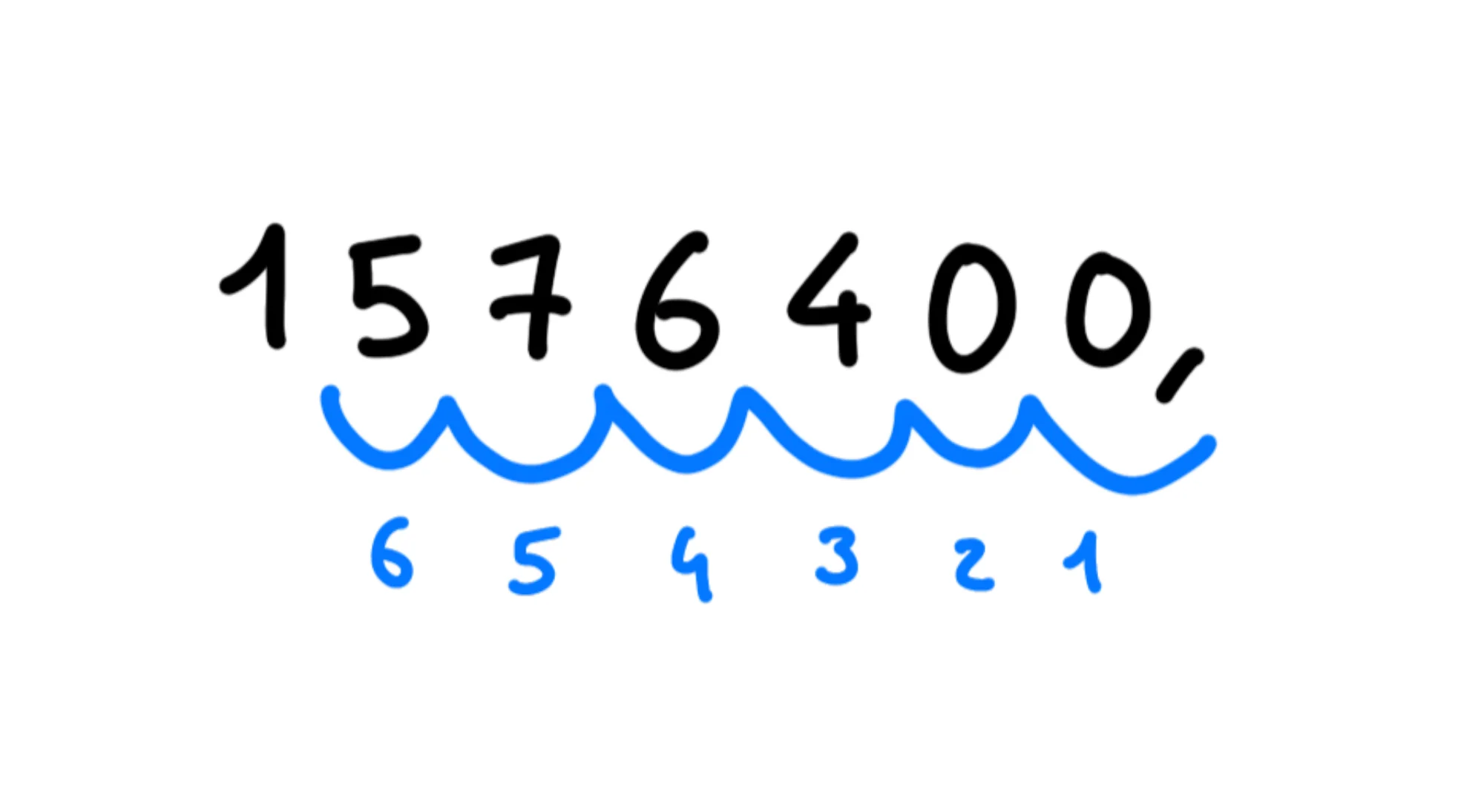
Il numero di salti che abbiamo fatto è uguale alla potenza di per cui dobbiamo moltiplicare il nuovo numero:
Gli ultimi due zeri (se non sono cifre significative) sono inutili, quindi possiamo toglierli ed ottenere:
Se invece abbiamo un numero minore di come allora dobbiamo spostare la virgola verso destra finché non superiamo il primo numero diverso da
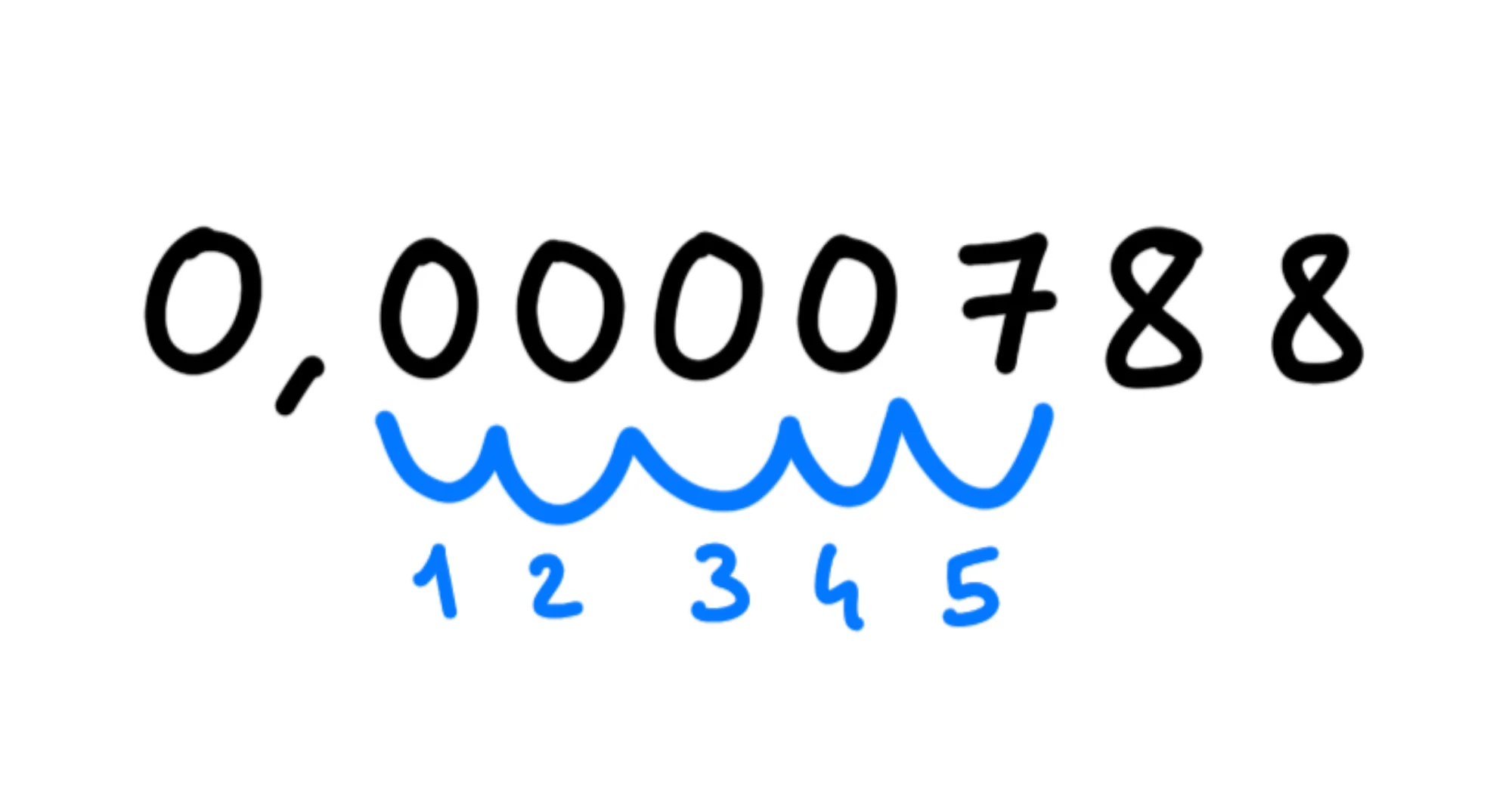
Siccome, però, questa volta stiamo spostando la virgola verso destra, l'esponente sarà negativo. Dunque avremo:
In generale, quindi, un numero scritto in notazione scientifica è un numero compreso da e moltiplicato per una potenza di
Una delle ragioni l'abbiamo vista prima: ci permette di scrivere in maniera più concisa numeri molto grandi o molto piccoli.
Ma c'è anche un'altra ragione:
Se prendo cioè centoquarantamila, e non uso la notazione scientifica, mentre lo scrivo potrei dimenticarmi uno E non sarebbe un piccolo errore perché otterrei cioè quattordicimila, un decimo del numero iniziale.
Se invece uso la notazione scientifica, il numero diventa e se, per una questione di cifre significative, dovessi scrivere comunque gli zeri infondo ed ottenere se mi dovessi dimenticare di scrivere uno cambiandolo in non succederebbe quasi nulla. Avrei comunque sempre centoquarantamila e avrei solo perso una cifra significativa.