Funzioni
Di seguito analizzeremo le funzioni.
Cos'è una funzione?
Una funzione è una corrispondenza (o legge) tra gli elementi di un insieme, dominio, e quelli di un altro insieme, il codominio. Ad ogni elemento del dominio deve essere associato uno ed un solo elemento del codominio. Su un piano cartesiano, il dominio comprende i valori delle x, mentre il codominio quelli delle y.
Quindi, chiamato l’insieme dominio A e l’insieme codominio B (o immagine di A mediante la funzione f), assegniamo ad ogni elemento a di A un elemento b di B:
f:a \rightarrow bE scriviamo che:
f(a)=b
Questa è la scrittura matematica per dire che assegnamo ad a il valore b in funzione di f.
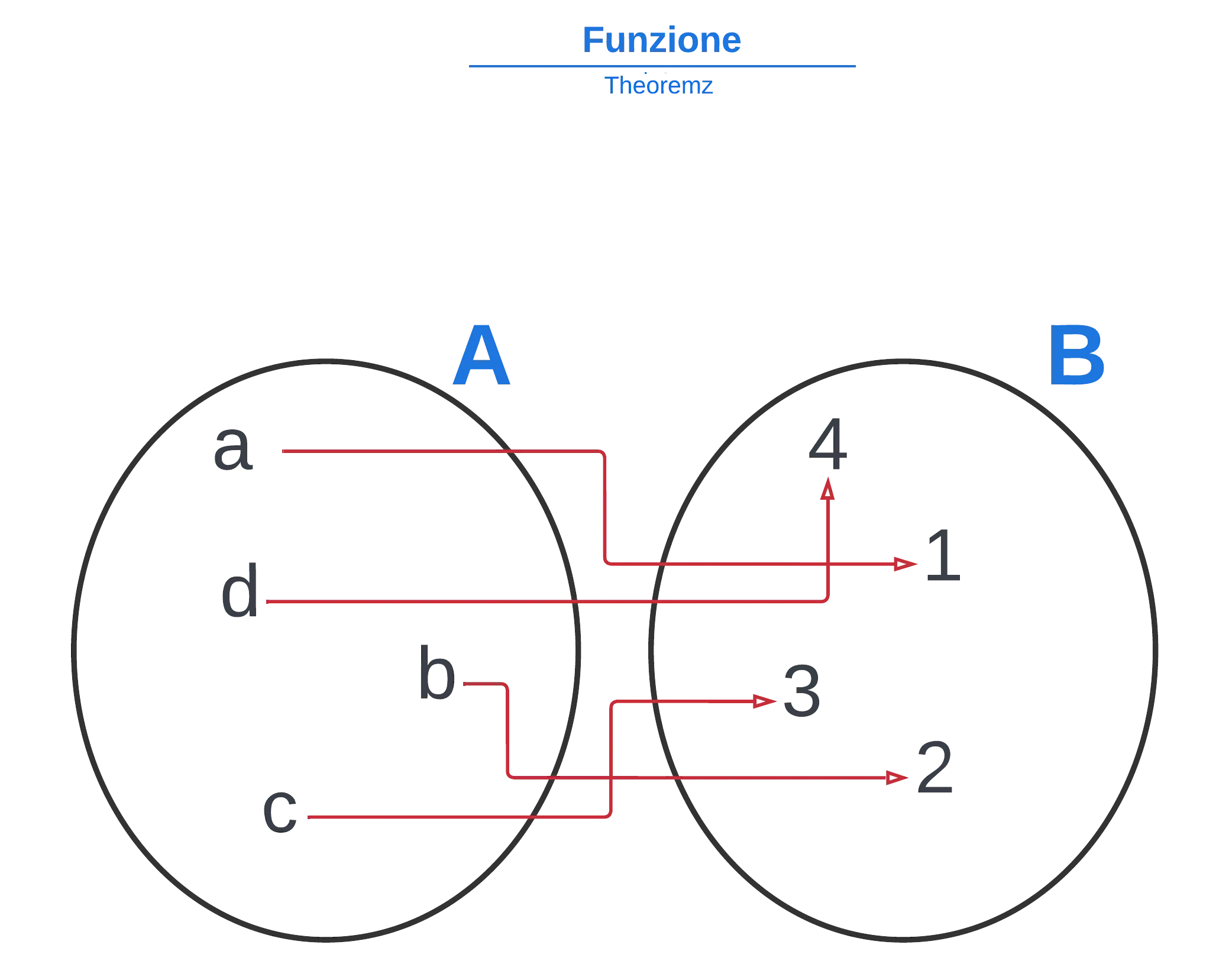
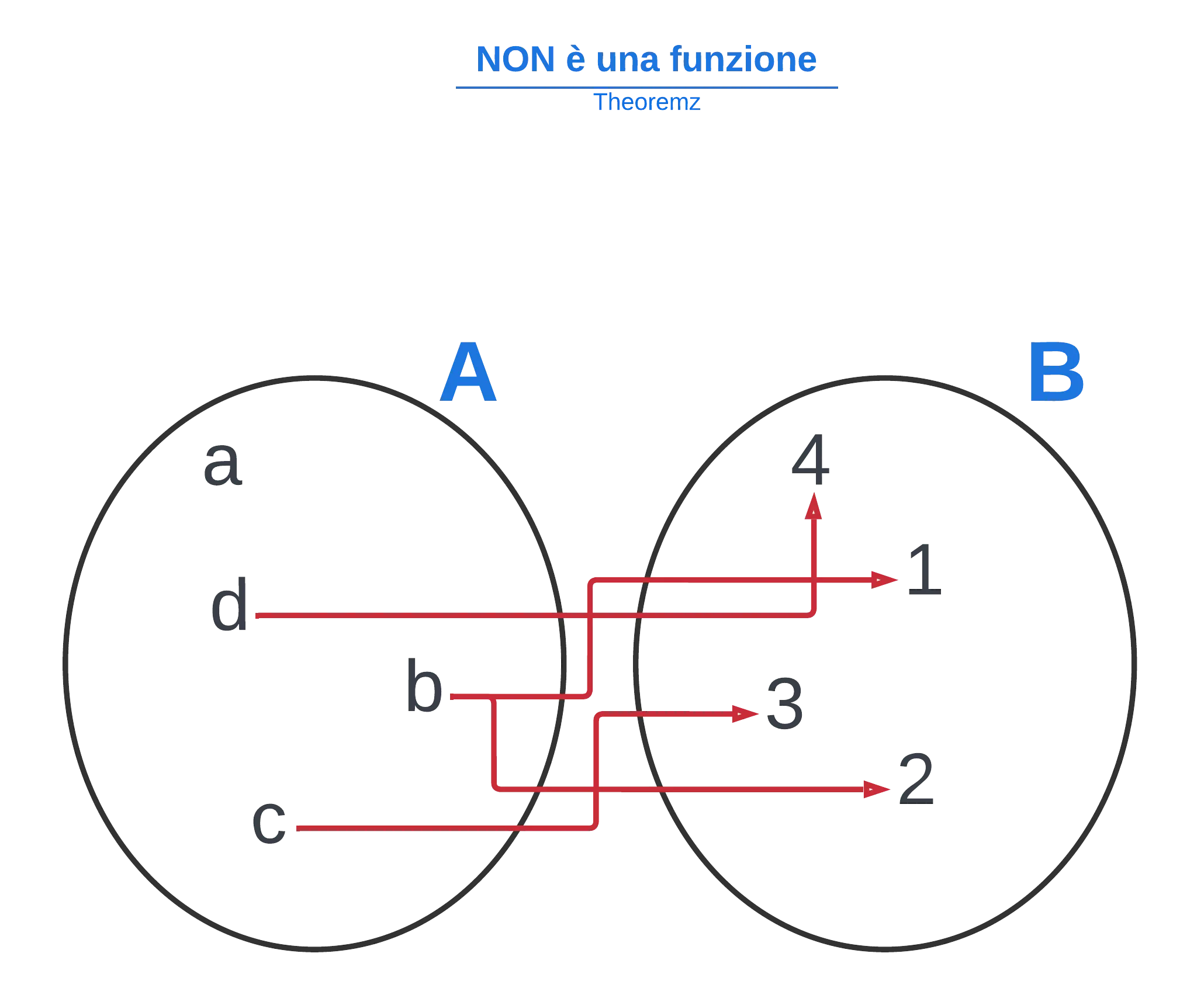
Fai attenzione, una funzione deve portare ogni elemento di A ad uno ed un solo elemento di B. Quindi se porta un elemento di A a più elementi di B, non è una funzione.
Classificazione delle funzioni
Prima di studiare una funzione è importante classificarla.
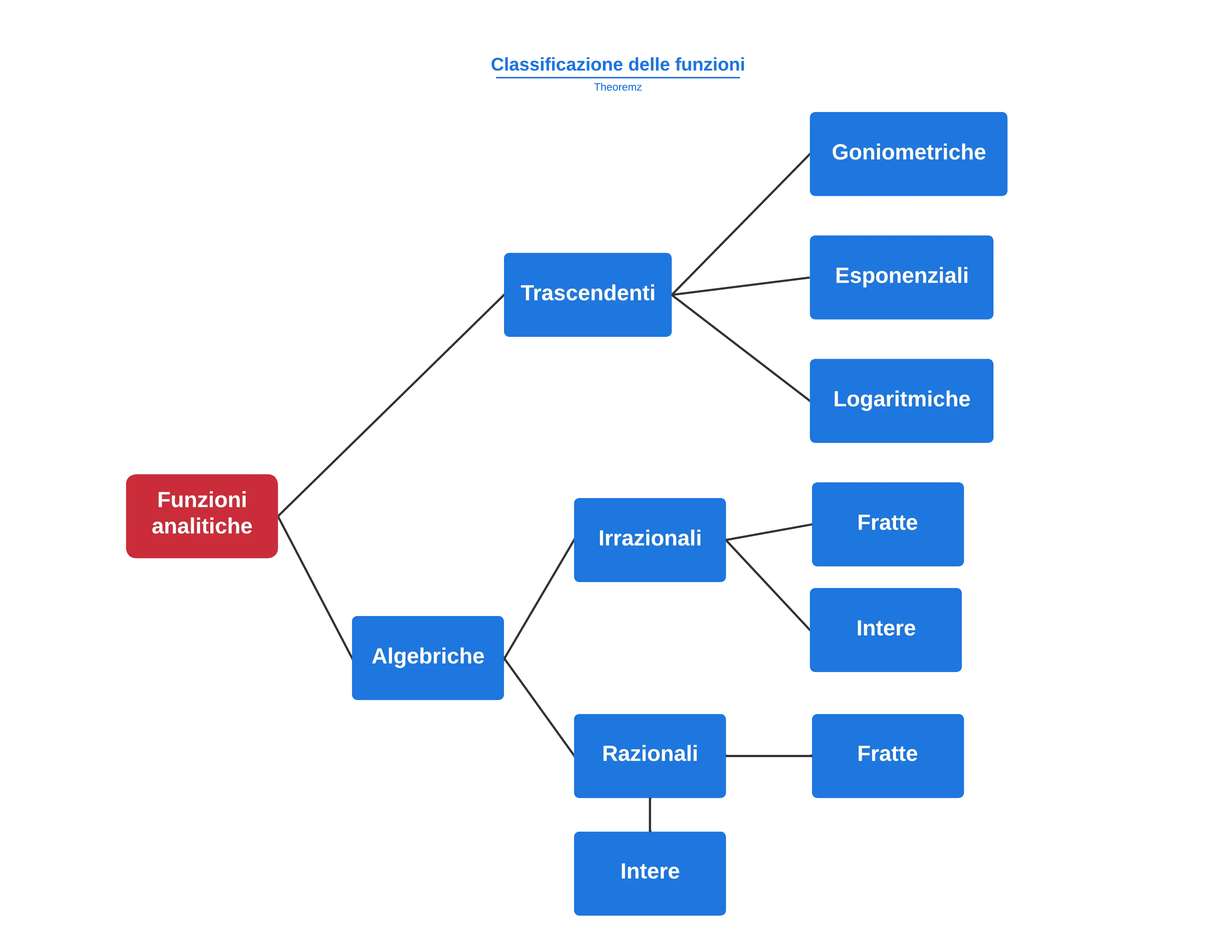
Di seguito uno schema sulla classificazione delle funzioni:
Legge di una funzione
La legge di una funzione è la regola che definisce la corrispondenza tra i due insiemi. Una legge di una funzione può essere espressa in qualunque forma, vale a dire che non deve essere obbligatoriamente scritta in lettere, numeri o simboli matematici, bensì può anche essere enunciata a voce.
Esempio di legge di una funzione:
Descrizione a parole:
Dati gli insiemi A=(\mathbb{N}) e B = (tutti i numeri pari), la legge che associa ogni numero naturale al suo doppio.
Definizione analitica:
f:N\rightarrow N (definita nell’insieme dei numeri naturali)
y = 2x
Studio di funzione basilare
Per studiare una funzione, è necessario svolgere più passaggi, l’ordine dei passaggi non è importante ma noi li riportiamo nell’ordine che consideriamo più facile e intuitivo.
1) Studio del dominio
Il dominio della funzione, come detto in precedenza, è l’insieme degli elementi del primo insieme. Molte volte si dà per scontato che il dominio comprenda tutti i numeri reali ma spesso capita che alcuni numeri in particolare siano da escludere per vari motivi.
Potrebbe capitare, ad esempio, una funzione di questo tipo:
y=\sqrt{x}
a primo impatto un occhio allenato si accorgerebbe che questa funzione non è definita per tutti i numeri reali. Infatti, se la x dovesse essere un numero negativo la funzione sarebbe indefinita.
Quindi come fare lo studio del dominio? In questo caso è facile, basta escludere i numeri negativi e il gioco è fatto. Ma in altre situazioni potrebbe capitare di dover porre il denominatore \neq 0, il radicando \geq 0, l’argomento di un logaritmo >0 ecc…
Una volta trovato il dominio lo possiamo scrivere in questa forma:
D_x: l'intervallo delle x per i quali la funzione è definita
Esempio:
y=\sqrt x \rightarrow D_x: [0, +\infty[
In alcuni casi il dominio è già dato dal testo degli esercizi.
2) Trovare le intersezioni con gli assi
Questo passaggio consiste nel trovare i valori di x per cui y è uguale a 0 e viceversa. Per fare questo ci basterà sostituire prima la x e poi la y con 0 e risolvere le equazioni.
Esempio:
y=4x-3 \longrightarrow D_x: x \in R
x=0\longrightarrow y= 4\cdot 0 - 3 = -3
Quindi l'intersezione con l'asse delle y avviene nel punto (0;-3).
x=0\longrightarrow 0= 4x - 3 \longrightarrow 4x= 3 \longrightarrowx={3\over 4}
Quindi l'intersezione con l'asse x avviene nel punto ({3\over 4}; 0)
In questo caso la funzione è una retta ed ha solo un’intersezione con l’asse delle ascisse ma può succedere che ce ne siano di più.
3) Studio del segno
Lo studio del segno consiste nel trovare i valori per cui la y è positiva e quindi, nel piano cartesiano, dove la funzione è sopra l’asse delle ascisse.
Per fare questo è necessario porre la funzione >0 e risolvere la disequazione.
Esempio:
y=4x-3 \longrightarrow D_x: x \in R
4x-3>0 \longrightarrow x>{3\over 4}
Il risultato saranno i valori della x per cui la funzione è positiva. Da questi ricaviamo i valori per cui la funzione è negativa, che saranno tutti gli altri valori del dominio.
Esempio:
y=4x-3 \longrightarrow D_x: x \in R
Funzione positiva \longrightarrow x>{3\over 4}
Funzione negativa \longrightarrow x < {3\over 4}
4) Disegnare il grafico
L’ultimo passo è, ora che abbiamo molte più informazioni sulla nostra funzione, rappresentarla sul piano cartesiano.
Per questa lezione ci fermeremo alla rappresentazione delle zone dove la funzione è positiva o negativa e delle intersezioni con gli assi cartesiani.
Il primo passo è disegnare il nostro grafico e escludere le zone dove la funzione non è definita, questi dati li abbiamo ricavati prima nello studio del dominio.
Nel nostro esempio, il dominio coincide con l'insieme dei numeri reali, quindi non ci sono zone da escludere:
Il secondo step è rappresentare le intersezioni con gli assi, queste sono gli zeri della funzione trovati in precedenza.
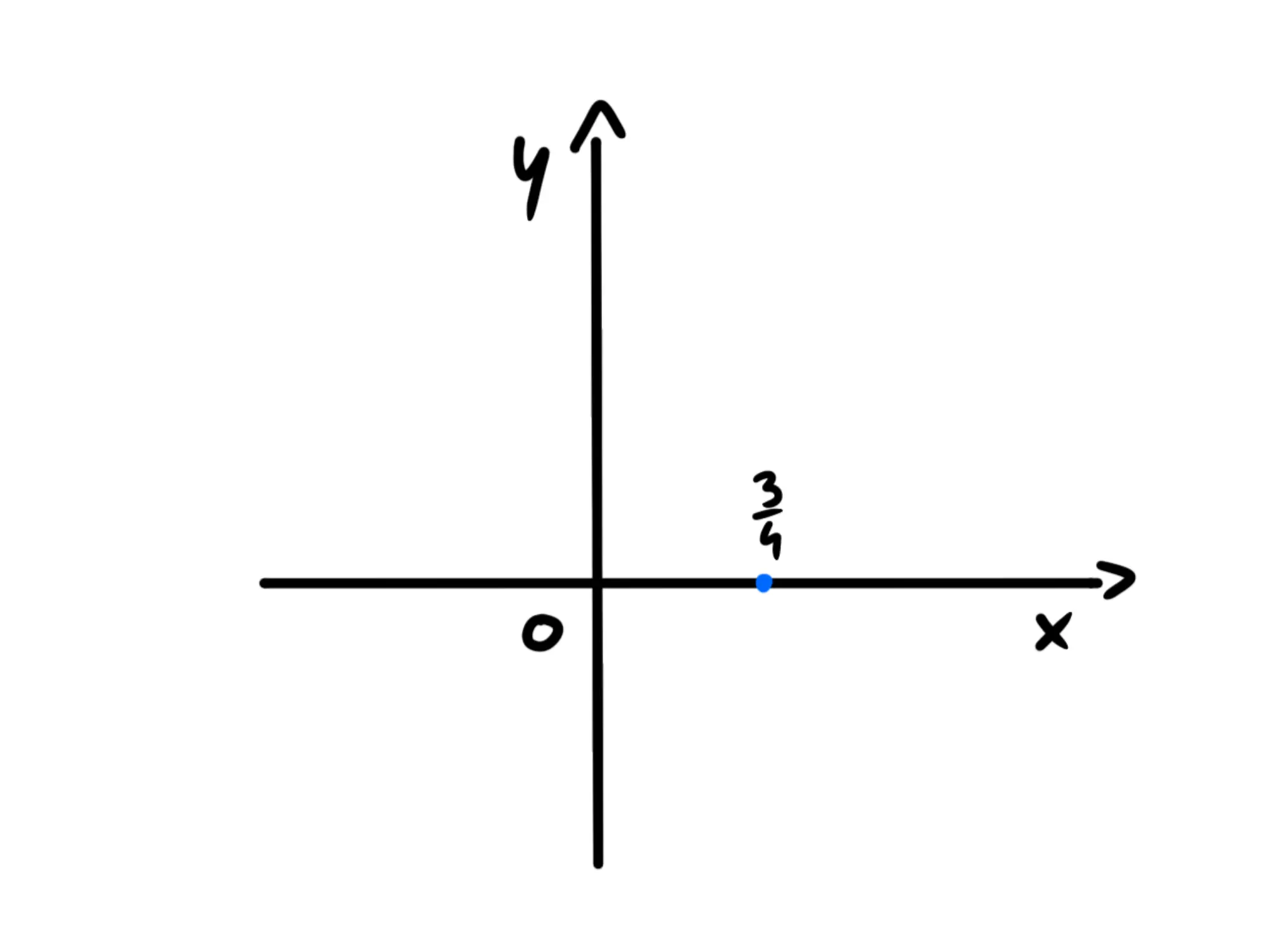
Ora rappresentiamo le zone dove la funzione è positiva o negativa basandoci sul nostro studio del segno e sulle intersezioni con l’asse delle ascisse. In una zona che sarà sicuramente positiva cancelliamo la parte negativa.
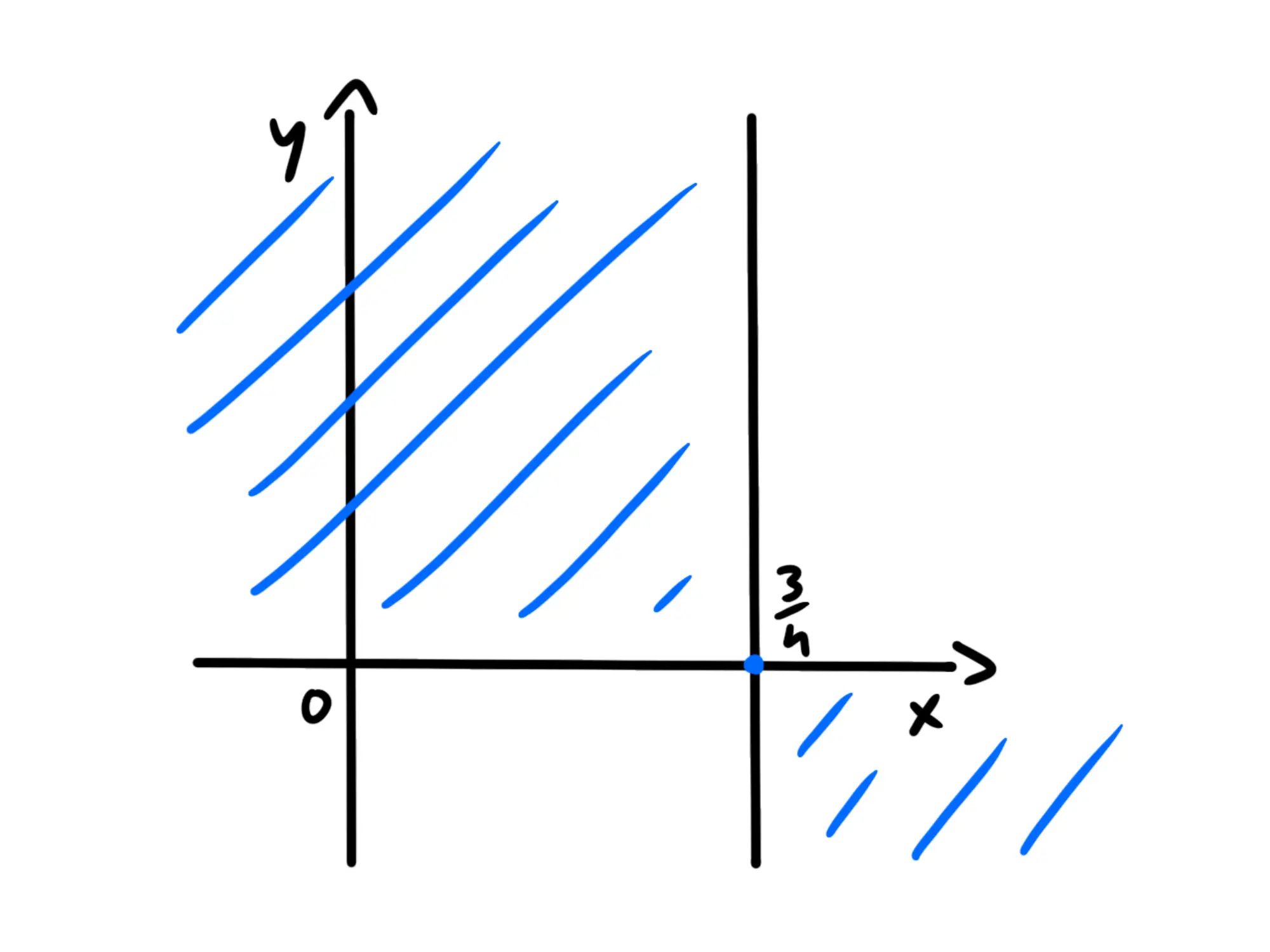
Finito, abbiamo studiato la nostra funzione!
Funzioni iniettive
Una funzione si dice iniettiva se ad ogni elemento del codominio è associato a non più di un elemento del dominio, e quindi in una rappresentazione grafica gli elementi di B sono raggiunti da una freccia sola.
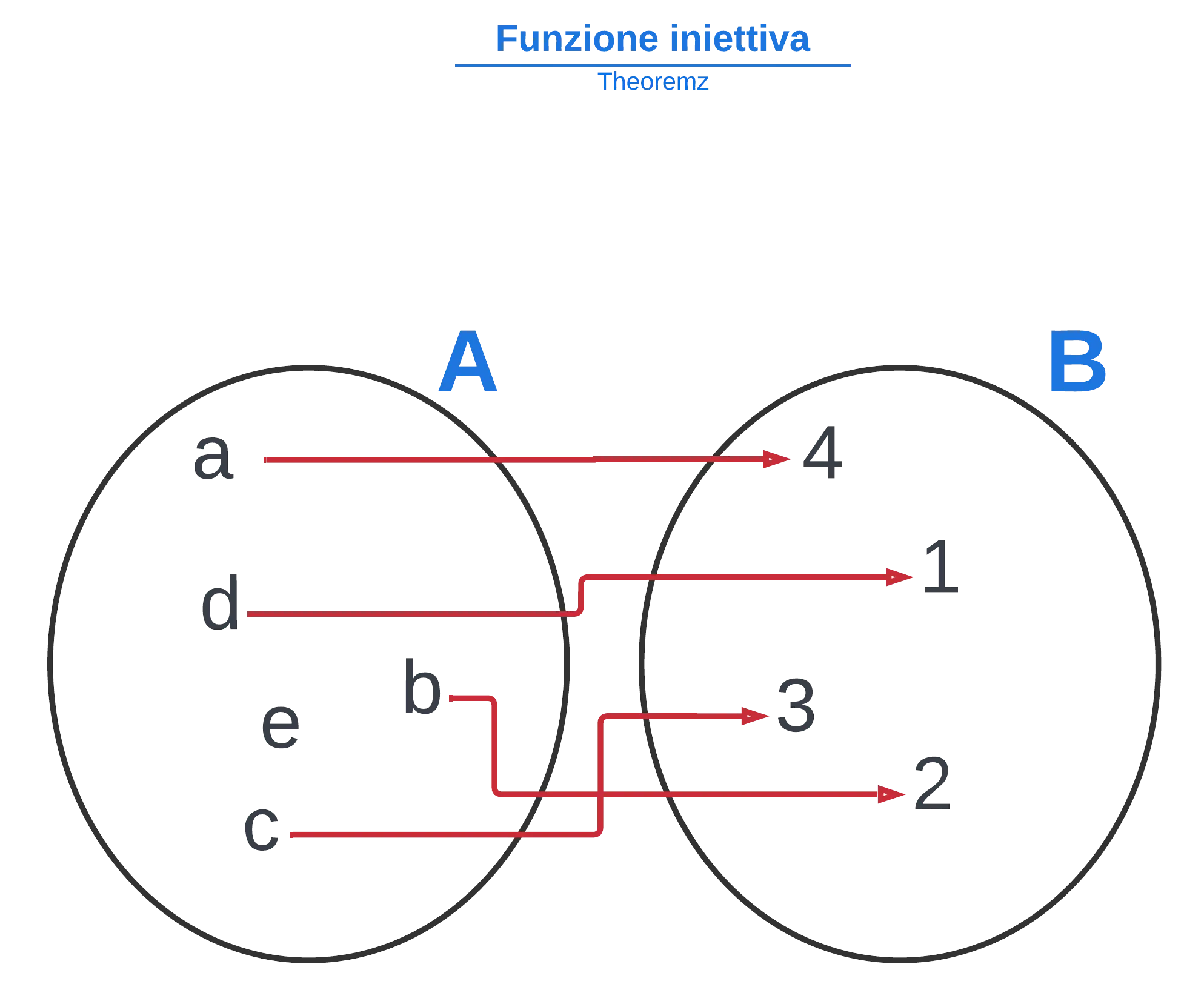
Se possiamo rappresentare la nostra funzione sul piano cartesiano, essere iniettiva significa non tornare mai alla stessa altezza due volte.
Funzioni suriettive
Una funzione si dice suriettiva se tutti gli elementi del codominio sono associati ad almeno un elemento del dominio, quindi in una rappresentazione grafica tutti gli elementi di entrambi gli insiemi saranno coinvolti in almeno una corrispondenza.
In altre parole, una funzione è suriettiva se "arriva" a tutti gli elementi del codominio.
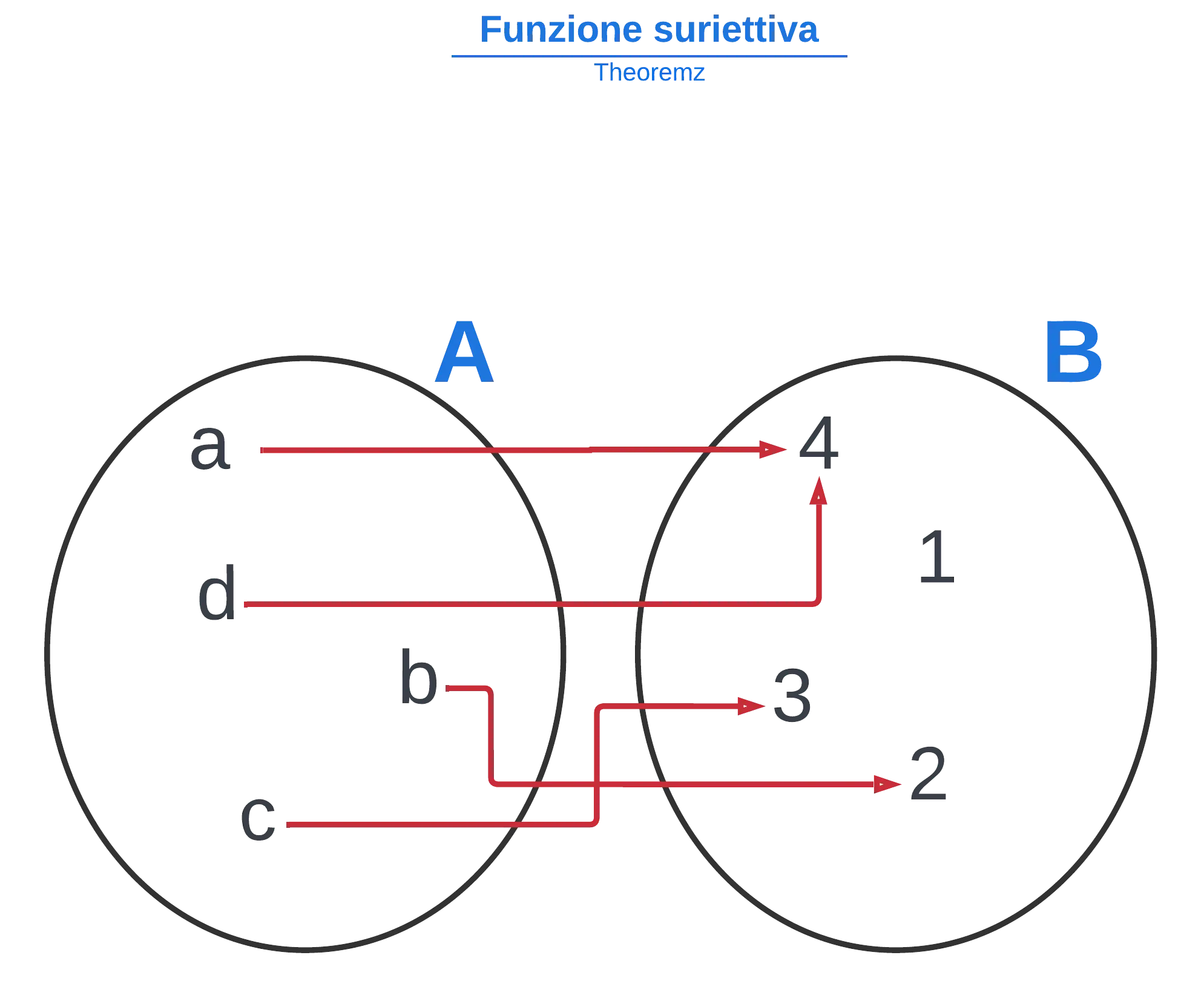
Funzioni biettive
Una funzione si dice biettiva se è sia suriettiva che iniettiva allo stesso tempo. Quindi ogni elemento del dominio è collegato ad uno ed un solo elemento del codominio e ogni elemento del codominio viene assegnato ad uno ed un solo elemento del dominio.
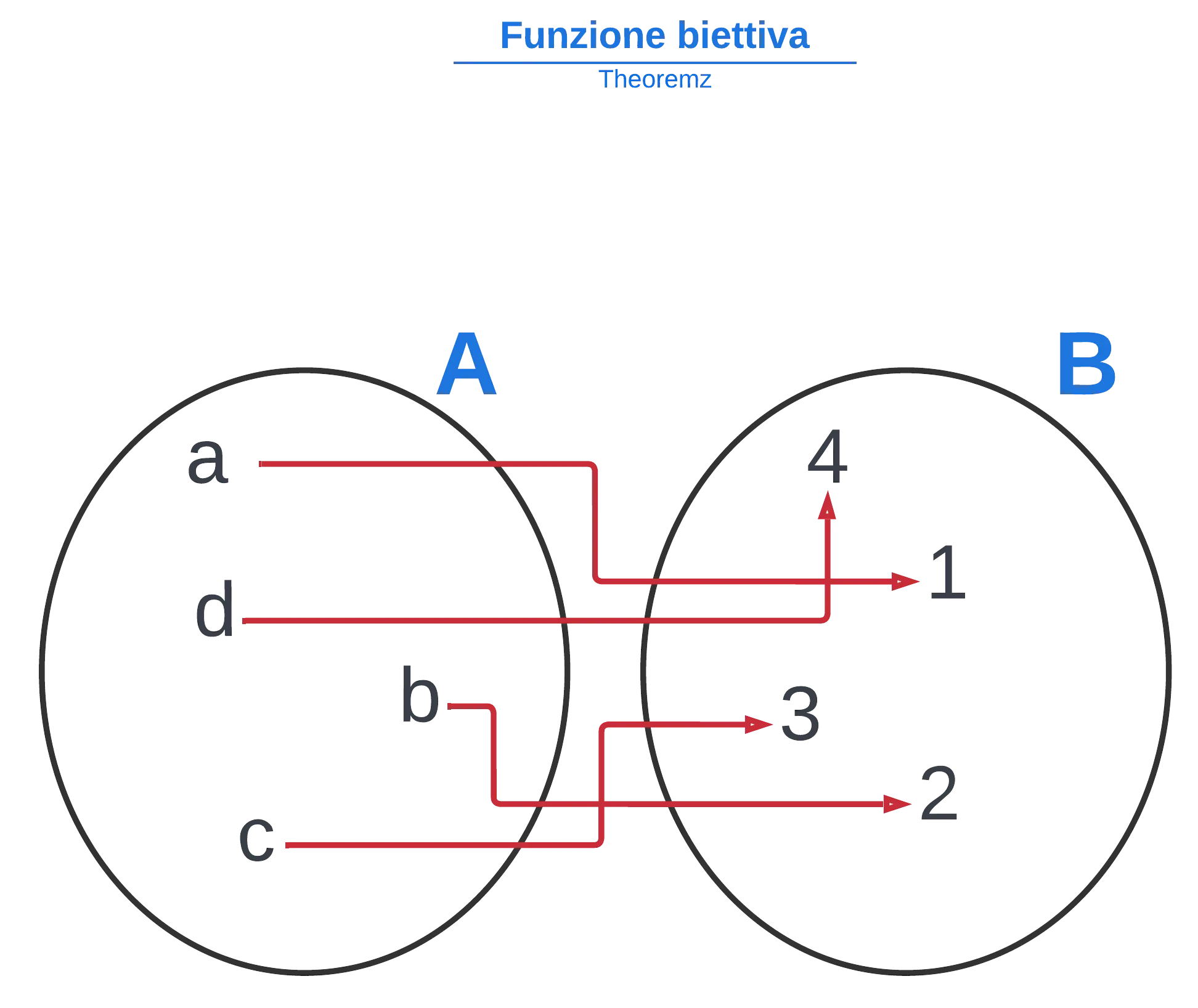
Funzione invertibile
Una funzione invertibile è una funzione per la quale è possibile definire una funzione inversa.
Una funzione è invertibile solo se è biettiva.
Una funzione inversa è una funzione con una legge opposta alla legge della funzione di partenza e che quindi possiamo vedere come la funzione di partenza con le frecce al contrario.
Di conseguenza la funzione inversa di una funzione sarà identica alla prima ma con gli insiemi invertiti:
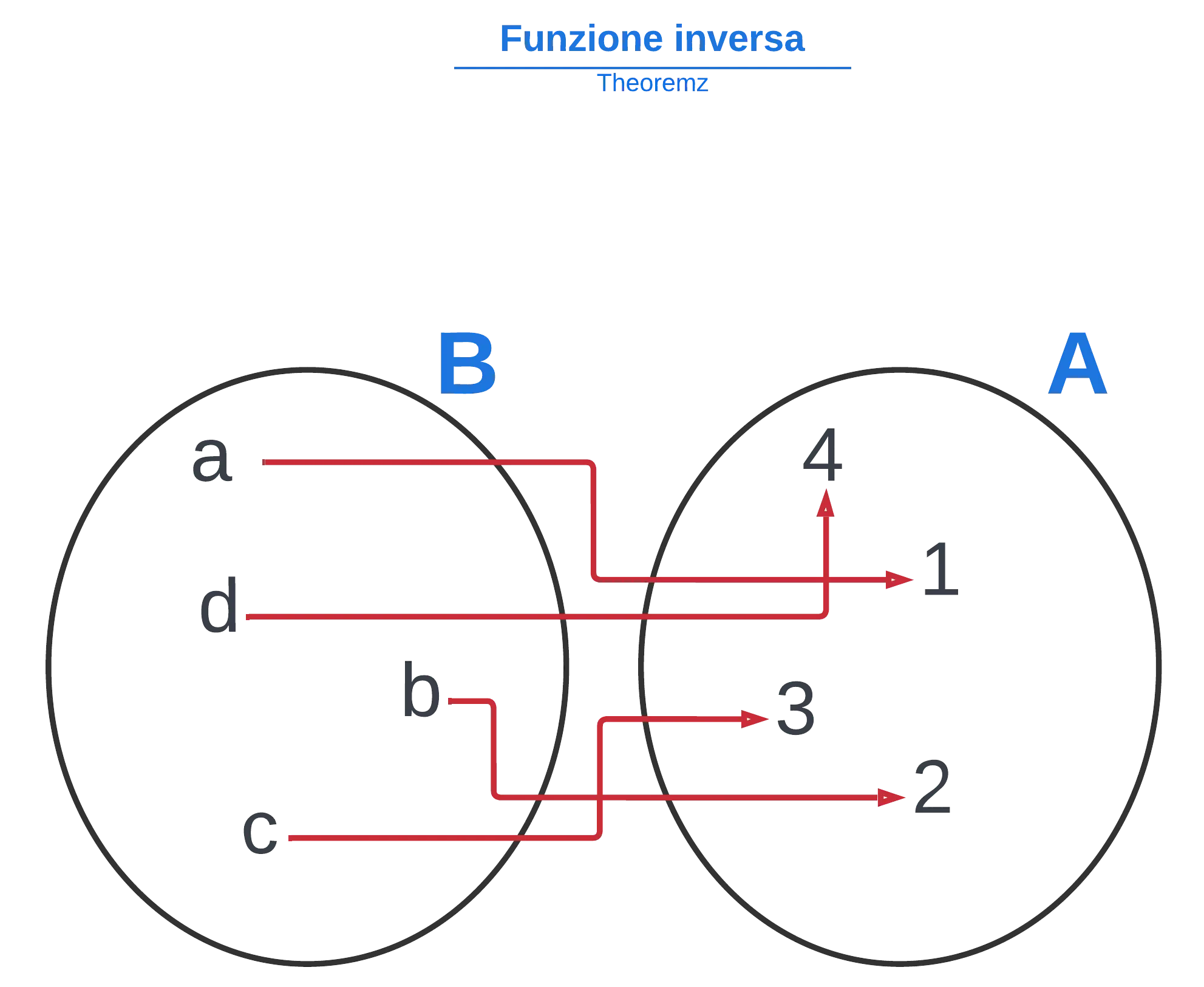
Come trovare una funzione inversa
Per trovare una funzione inversa bisogna per prima cosa verificare se la funzione di partenza è sia iniettiva che suriettiva e quindi biunivoca (cioè biettiva).
Dato che una funzione inversa può essere vista semplicemente come una funzione con i insiemi invertiti, dovremo prendere la nostra funzione di partenza e scambiare il codominio con il dominio.
Cioè se prima avevamo isolato la y in funzione di x, adesso dobbiamo isolare la x in funzione di y.
Esempio:
y=2x
x={y \over2 }
Siccome confonde un po' avere la x come variabile dipendente e la y come variabile indipendente, una volta trovata la funzione inversa, possiamo invertire le lettere. In questo caso avremo:
y ={x\over 2}
D'altronde, se la nostra funzione raddoppiava, appare logico che la sua funzione inversa dovrà dimezzare.
Ricordate che i valori di x per cui la funzione inversa è definita non sono sempre gli stessi della funzione di partenza, quindi ricordatevi di studiare il dominio di nuovo se necessario.