Moto rettilineo uniforme

Moto Rettilineo uniforme

Il moto rettilineo uniforme è la più semplice tipologia di moto nel piano. Per questo inizieremo da esso.

Il suo nome ci dice tutto:

Il moto rettilineo uniforme descrive il moto dei corpi che si muovono lungo una traiettoria retta a velocità costante.

Legge oraria

Per studiare qualsiasi moto dobbiamo prima conoscere la legge oraria, ovvero la relazione che lega lo spazio percorso con il tempo trascorso per percorrerlo. Nel moto rettilineo uniforme, per conoscere la legge oraria ci basta avere 3 dati:

Ci serve la velocità v, che in un moto rettilineo uniforme è costante, lo spazio iniziale S_0, che dipende dalla posizione dell’osservatore (solitamente per facilitare si mette 0) e t_0 (che, se possibile, si mette anch’esso uguale a 0).

Cerchiamo quindi una legge, una formula, che ci dice come varia la posizione del corpo in funzione del tempo conoscendo questi tre dati.

Prima di farlo dobbiamo però definire precisamente che cosa intendiamo con "velocità".

Definiamo quindi una nuova grandezza fisica: la velocità media.

La velocità media è uguale allo spazio percorso diviso il tempo impiegato, ovvero:

{v}_{m}=\frac{{S}_{1}-{S}_{0}}{{t}_{1}-{t}_{0}}

Siccome nel nostro moto la velocità è costante, possiamo chiamare la velocità media v_m come una più generale velocità v.

Quello che a noi interessa è lo spazio finale, cioè S_1. Per trovarlo ci basta usare la formula della definizione della velocità media. Isolandolo, infatti, otteniamo:

S_{t}=S_0+v \cdot (t-t_0)

Che sarà proprio la legge oraria del moto rettilineo uniforme.

Abbiamo detto che questo corpo si muoverà lungo una retta, ma una retta è infinita, quindi non ha un inizio. Non esiste dunque un punto di inizio, quindi come misurare lo spazio? Abbiamo bisogno di un sistema di riferimento.

Chimiamo il “punto 0” come origine è sarà dunque il punto che dista 0 metri, cioè è dove sta l'osservatore:

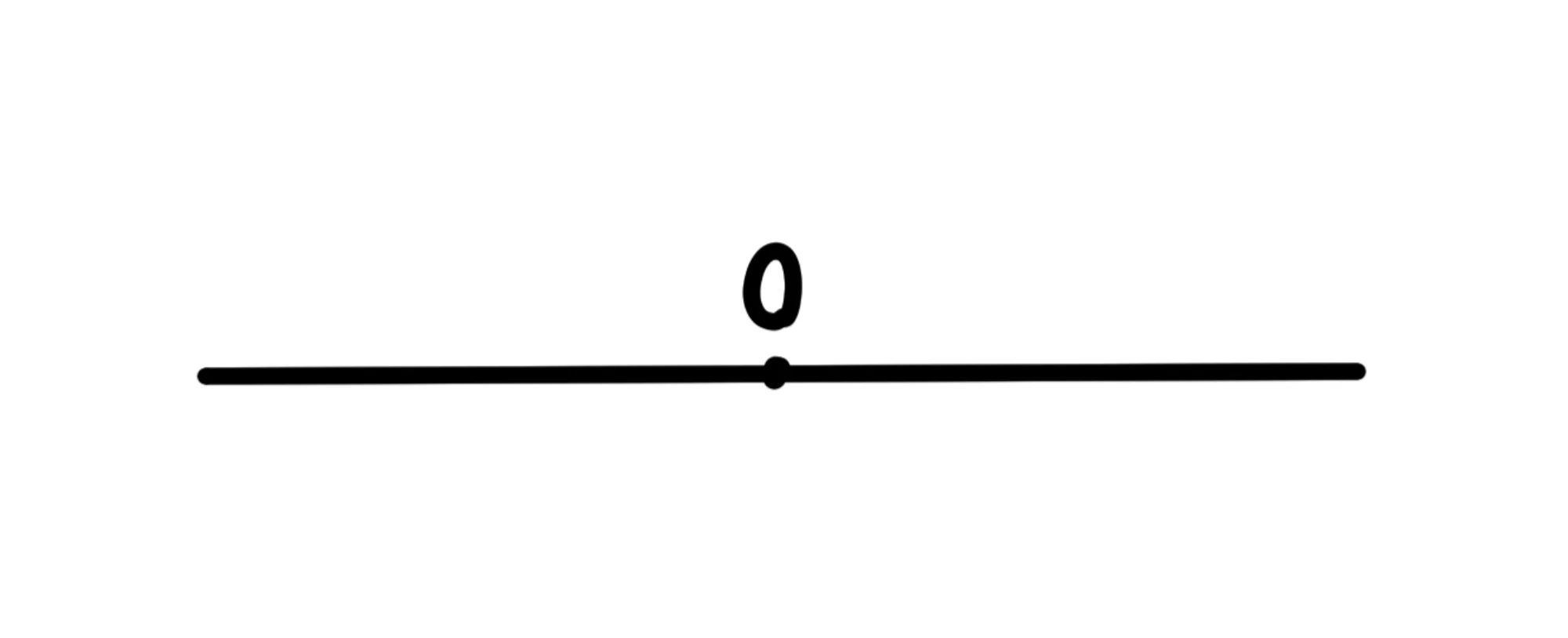
Infine, abbiamo bisogno di scegliere il verso. Infatti, spesso imponiamo che i numeri a destra dello 0 della retta siano positivi e quelli a sinistra siano negativi e quindi il verso è verso destra:

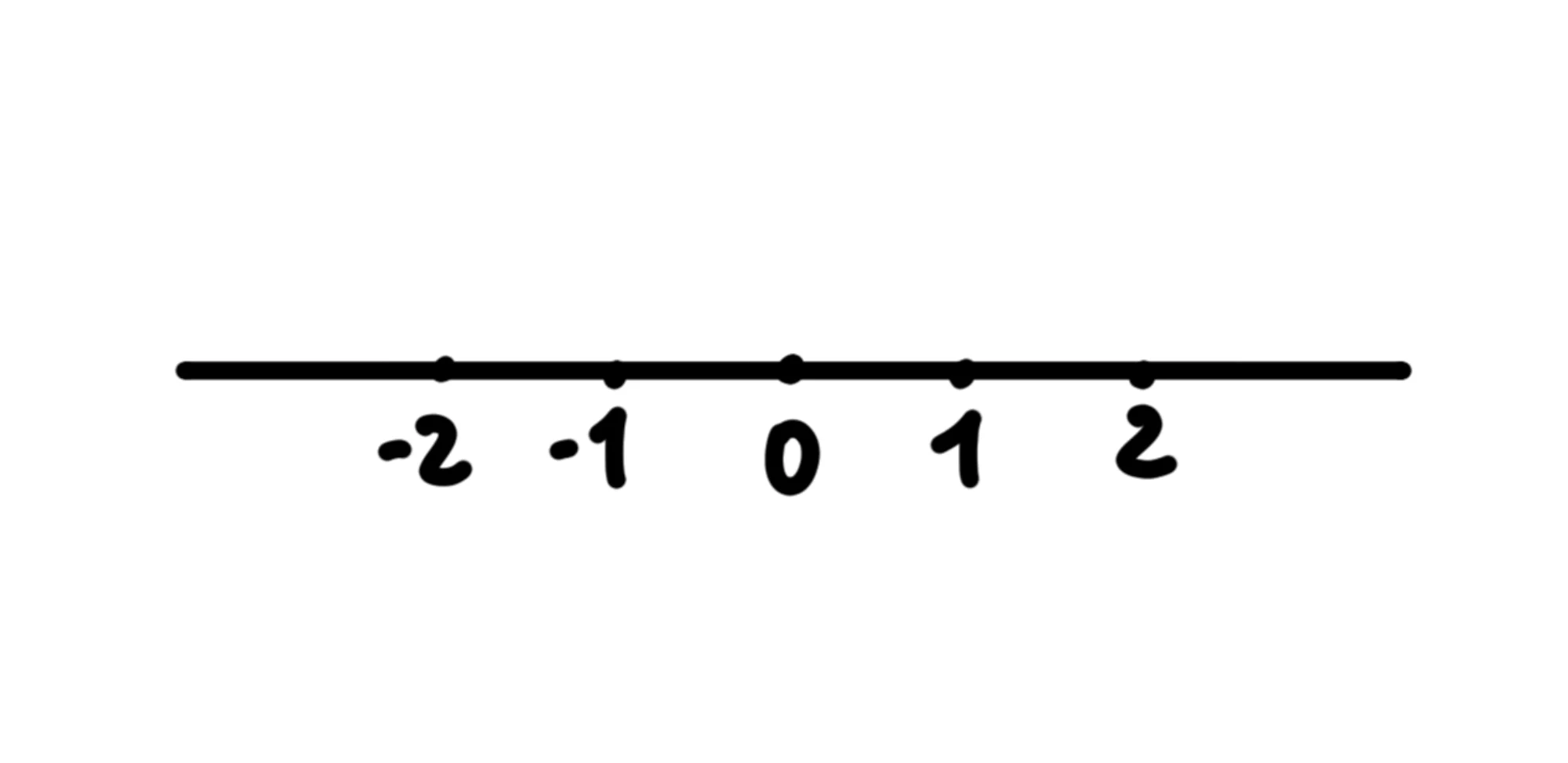
Potremmo però scegliere anche di mettere i numeri negativi a destra dell'uguale e quelli positivi a sinistra:

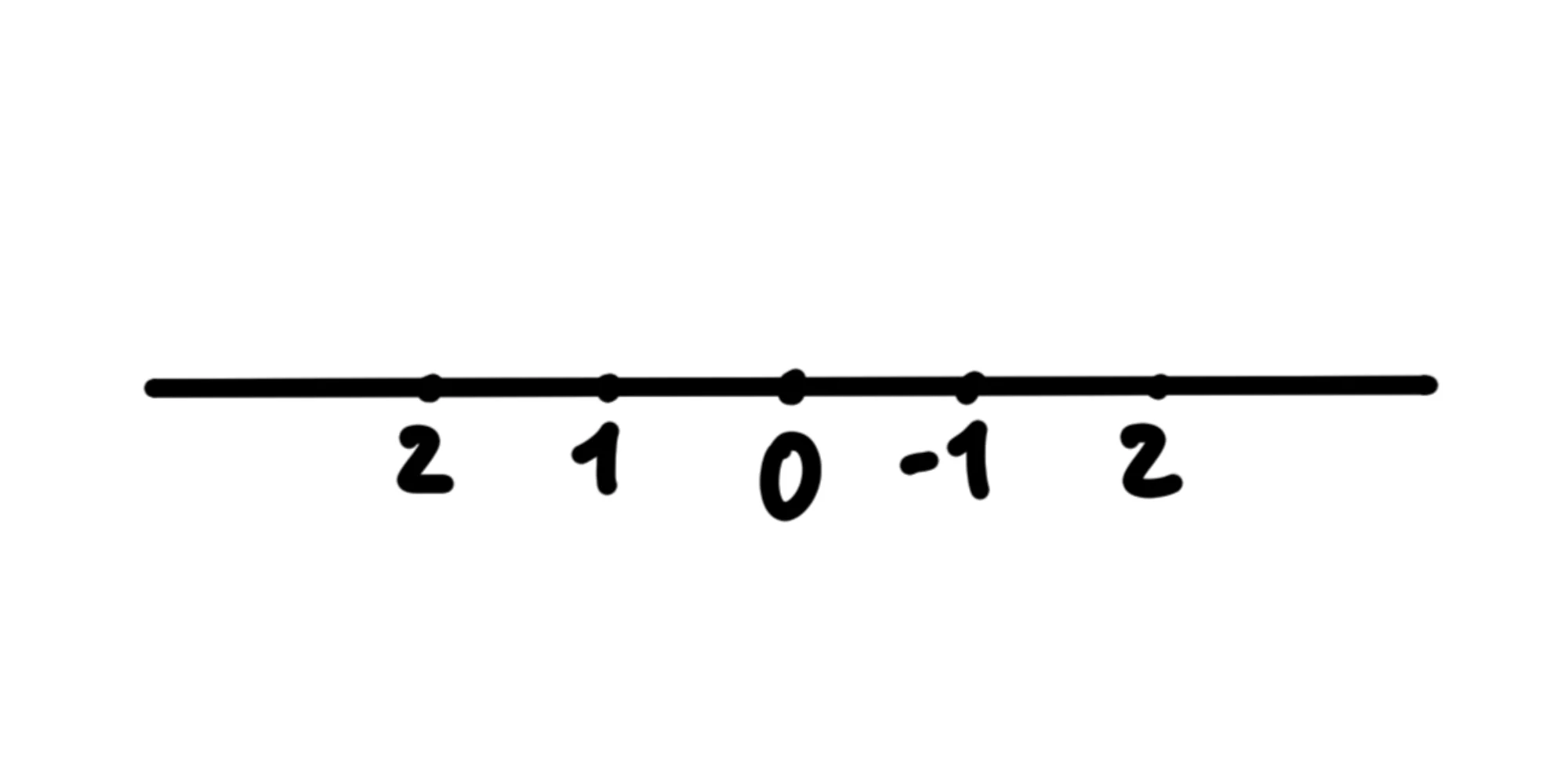
Questo può essere utile se un corpo si sta muovendo verso sinistra sulla retta. Dobbiamo dunque specificare quale verso stiamo usando. Per farlo, disegnamo una freccia verso la direzione in cui i numeri crescono:

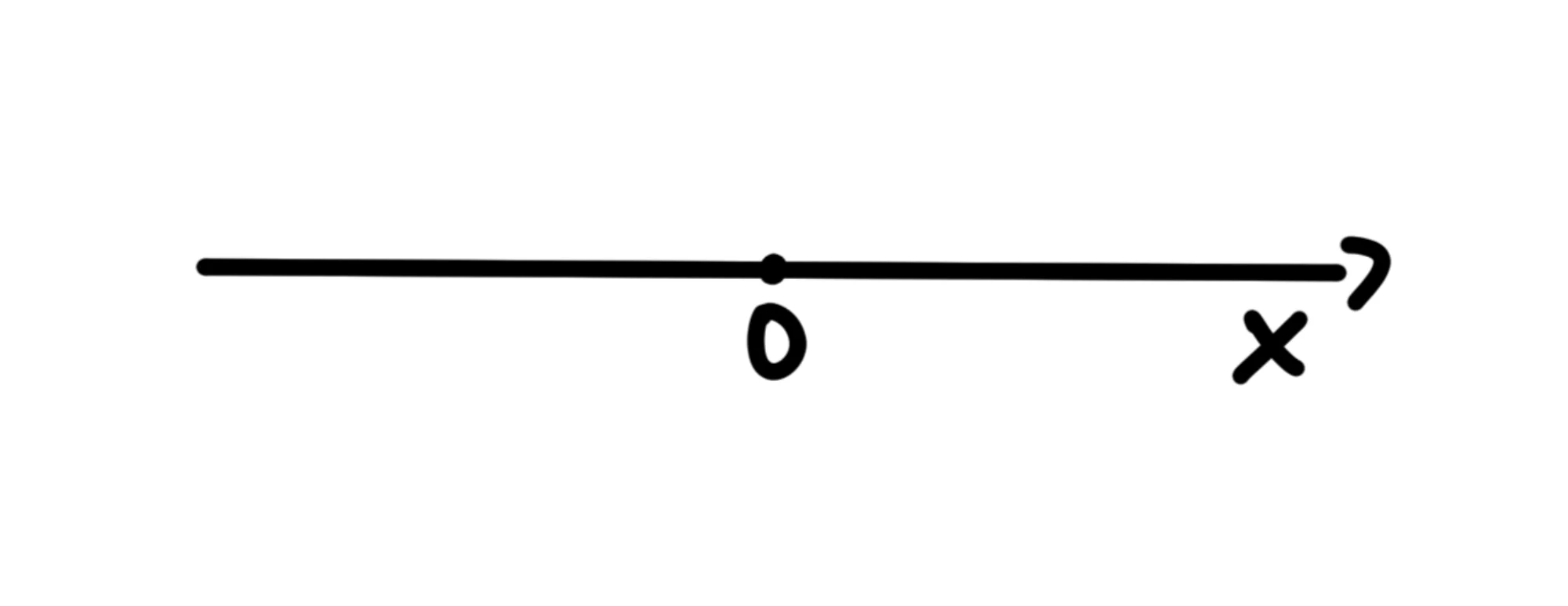
Spesso mettiamo pure una piccola x sotto la freccia, soprattutto se ci sono altre rette. In questo modo possiamo differenziarle.

Come abbiamo detto prima, solitamente si fa corrispondere l’origine ad S_0. Se poi siamo liberi anche di decidere da dove fare iniziare il tempo, conviene imporre anche t_0 pari a 0 secondi. In tal caso la nostra formula per la velocità si semplificherà in:

v=\frac{{s}_{1}-0}{{t}_{1}-0}=\frac{{s}_{1}}{{t}_{1}}

Quindi possiamo chiamare s_1 e t_1 genericamente come s e t:

v=\frac{s}{t}

In generale però non sempre possiamo decidere noi che valore dare a s_0 e a t_0, quindi è importante che vi ricordiate anche la formula generale.

Siccome S_1-S_0 e t_1-t_0 sono delle differenze, alcune volte si scrivono come \Delta S e \Delta t. Infatti, come forse già saprete, la lettera greca \Delta (Delta) sta, in questi casi, per “differenza di”. Quindi al posto di scrivere “differenza dello spazio (S_1-S_0)” scriviamo \Delta S.

Per questo su molti libri troverete scritta la formula per la velocità come:

v=\frac{\Delta S}{\Delta t}

Velocità media di due moti rettilinei uniformi

Immaginiamoci un corpo che si muove per un certo tratto (da S_0 a S_1) in un moto rettilineo uniforme a velocità v_1 e poi per un altro tratto (da S_1 a S_2) sempre in un moto rettilineo uniforme ma a velocità v_2. Possiamo trovare la velocità media di tutto il moto?

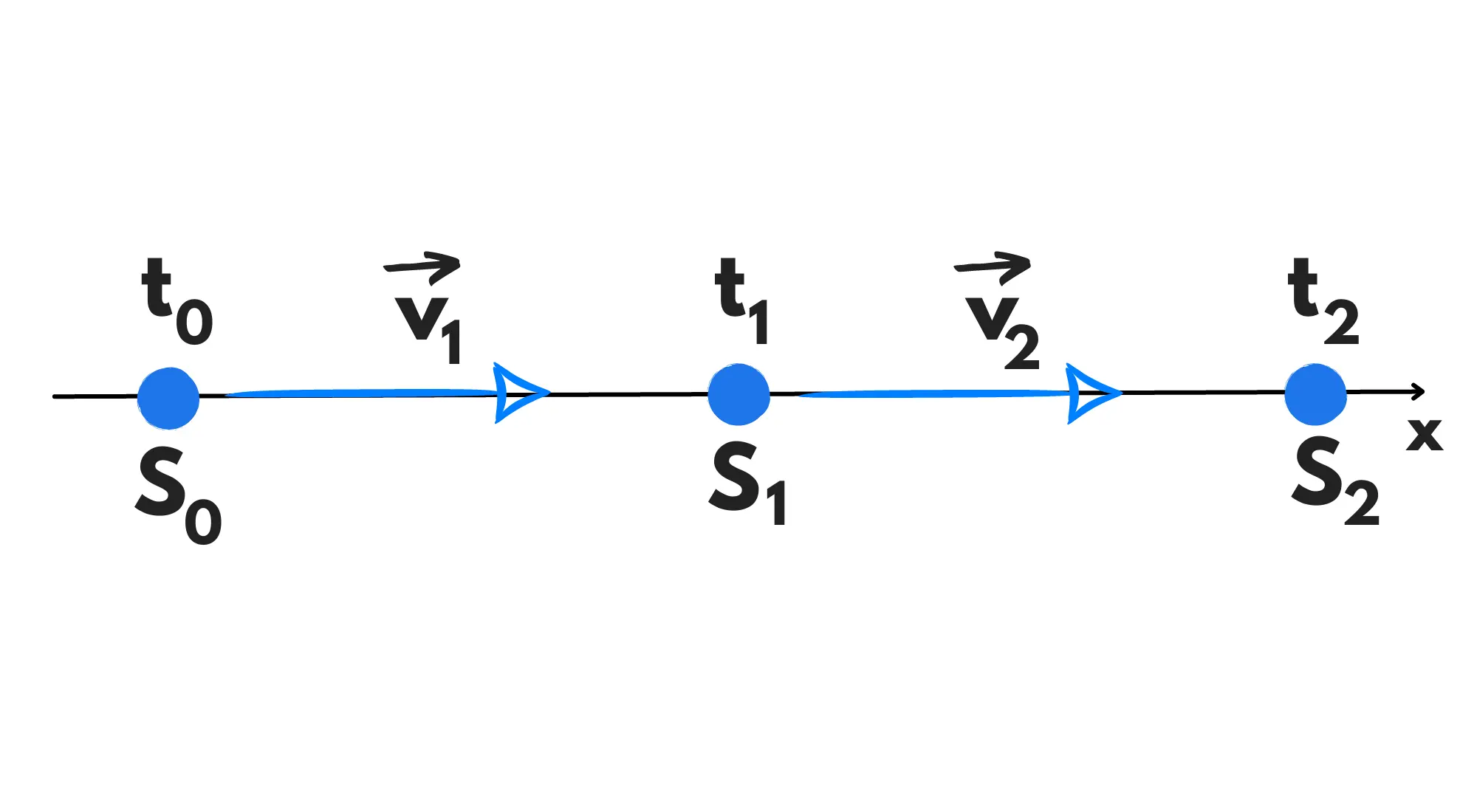
Di questo tipo di moto esistono due casi particolari che vengono spesso trattati con attenzione a scuola:

1) I due tratti sono uguali

Se i due tratti sono uguali, possiamo ricavarci facilmente la velocità media di tutto il moto sapendo le due velocità dei singoli tratti.

Al punto S_0, il tempo percorso sarà t_0, ad S_1 sarà t_1 e ad S_2 sarà t_2.

Dalle legge orarie dei due moti abbiamo:

S_1=S_0+v_1(t_1-t_0)

e

S_2=S_1+v_2(t_2-t_1)

Possiamo isolare le differenze dei tempi ed ottenere:

(t_1-t_0)=\frac{S_1-S_0}{v_1}

(t_2-t_1)=\frac{S_2-S_1}{v_2}

Abbiamo detto che i due tratti, cioè S_1 - S_0 e S_2 - S_1, sono uguali, quindi richiamiamo entrambi come s:

(t_1 - t_0) = \frac{s}{v_1}

(t_2-t_1) = \frac{s}{v_2}

Siamo pronti ora a trovare la velocità media v_m conoscendo soltanto v_1 e v_2:

Sappiamo che:

v_m=\frac{\Delta S}{\Delta t}

Quindi, siccome il nostro tratto inizia a S_0 e finisce a S_1, dobbiamo avere:

v_m=\frac{S_2-S_0}{t_2-t_0}

Possiamo aggiungere e sottrarre S_1 al numeratore, mentre aggiungiamo e sottraiamo t_1 al denominatore:

v_m=\frac{S_2-S_0+S_1-S_1}{t_2-t_0+t_1-t_1}

Riordiniamo:

v_m=\frac{S_2-S_1+S_1-S_0}{t_2-t_1+t_1-t_0}

v_m=\frac{(S_2-S_1)+(S_1-S_0)}{(t_2-t_1)+(t_1-t_0)}

Utilizziamo le due formule che abbiamo trovato prima per (t_1-t_0) e (t_2-t_1):

v_m=\frac{s+s}{{s \over v_1}+{s \over v_2}}

v_m={2s \over {{s\over v_1}+{s \over v_2}}}

v_m={2\over {{1\over v_1}+{1\over v_2}}}

Ovvero v_m è uguale alla media armonica tra v_1 e v_2.

2) I tempi trascorsi sono uguali

Le equazioni sono le stesse di prima, ma questa volta sono t_1-t_0 e t_2-t_1 ad essere uguali. Chiamiamo questa quantità t.

Questa volta però dalle leggi orarie vogliamo ricavare S_1-S_0 e S_2-S_1:

S_1=S_0+v_1t \longrightarrow S_1-S_0=v_1t

S_2=S_1+v_2t \longrightarrow S_2-S_1=v_2t

Ricordiamo che:

v_m=\frac{\Delta S}{\Delta t}=\frac{S_2-S_0}{t_2-t_0}

Anche questa volta aggiungiamo e sottraiamo al numeratore e S_1 al t_1 denominatore:

v_m=\frac{S_2-S_0+S_1-S_1}{t_2-t_0+t_1-t_1}

Riordiniamo e sostituiamo:

v_m=\frac{(S_2-S_1)+(S_1-S_0)}{(t_2-t_1)+(t_1-t_0)}

v_m=\frac{v_2t+v_1t}{t+t}

v_m=\frac{(v_1+v_2)t}{2t}

v_m={v_1+v_2 \over 2}

Ovvero v_m è uguale alla media aritmetica tra v_1 e v_2.