Le leggi di Keplero sono un insieme di tre leggi scoperte dall'astronomo tedesco Giovanni Keplero che descrivono il movimento dei pianeti.
In altre parole, sono tre leggi che ci dicono come orbitano i pianeti.
Per gran parte dell'antichità, si pensò che i pianeti seguissero delle orbite circolari. Keplero, però, scoprì che non era vero.
La prima legge di Keplero, infatti, afferma che l'orbita descritta da un pianeta è un'ellisse, di cui il Sole occupa uno dei due fuochi.
Cerchiamo di capire cosa significa questa frase:
Per prima cosa ci viene da chiederci che cosa sia un'ellisse. Potete pensare ad un'ellisse come ad un "cerchio schiacciato", come quello nella figura sottostante:

Matematicamente, si tratta di un oggetto ben definito da determinate regole geometriche, ma si tratta di concetti più avanzati che per il momento tralasceremo.
Se volete approfondirli potete consultare la nostra lezione sulle ellissi cliccando qui. Sappiate però che esiste una differenza matematica tra un semplice ovale ed un'ellisse.
La prima legge di Keplero ci dice inoltre che il Sole non sta al centro dell'ellisse, ma in uno dei suoi due fuochi.
I fuochi sono due punti che caratterizzano ogni ellisse (rendono le ellissi diverse).
Per adesso, ci basta sapere che più i due fuochi sono lontani e più l'ellisse appare schiacciata:


Se avviciniamo i fuochi così tanto da farli coincidere, l'ellisse diventa un cerchio.
Il nostro Sole si trova dunque in uno di quei due punti. Le ellissi delle orbite dei nostri pianeti sono quasi circolari, per questo ci è voluto tanto tempo prima che qualcuno se ne accorgesse.
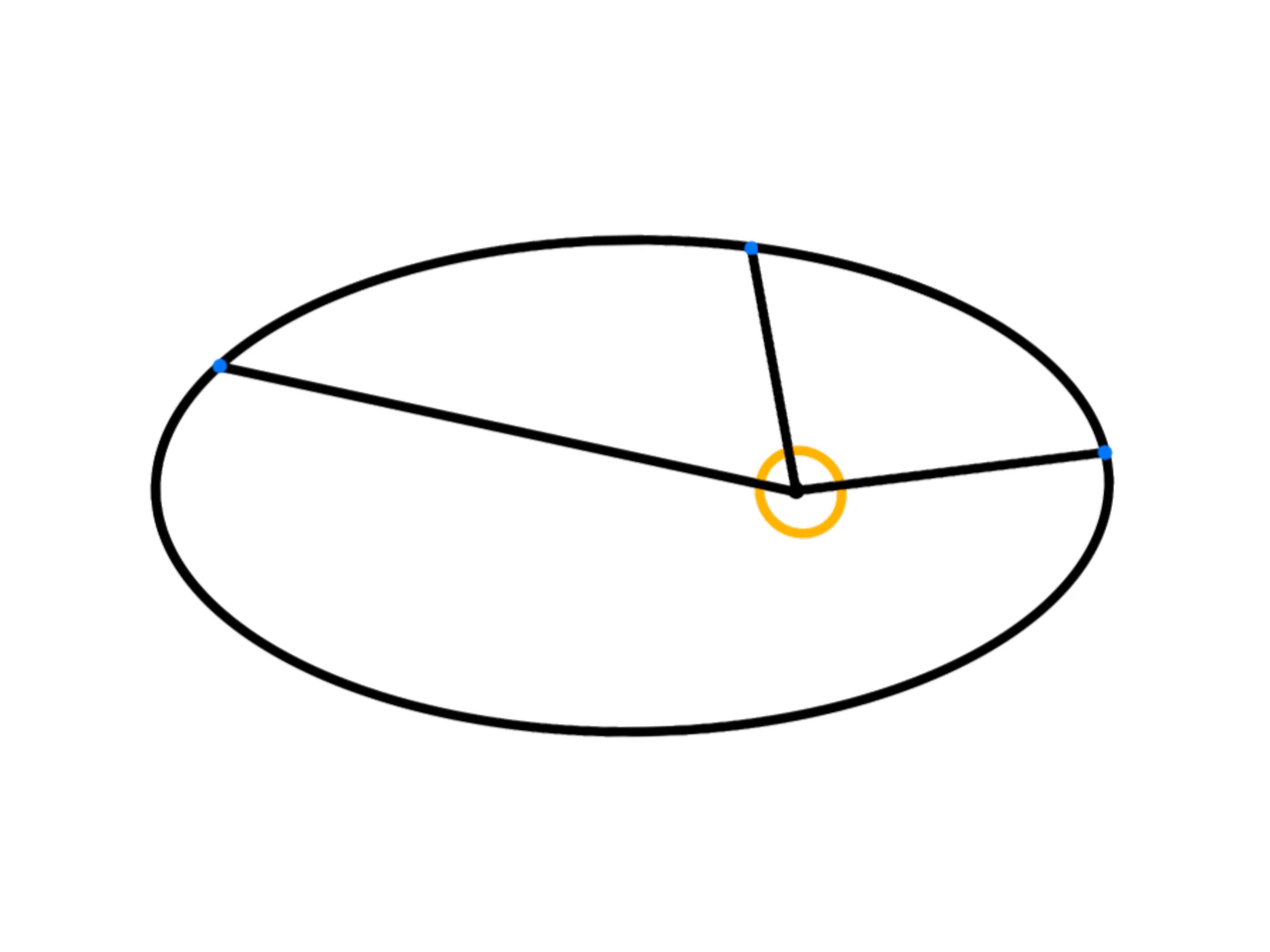
La seconda legge di Keplero afferma che il segmento che unisce il centro del Sole con il centro del pianeta descrive aree uguali in tempi uguali.
Tracciamo pezzo per pezzo gli elementi coinvolti in questo enunciato per capire graficamente che cosa significa:
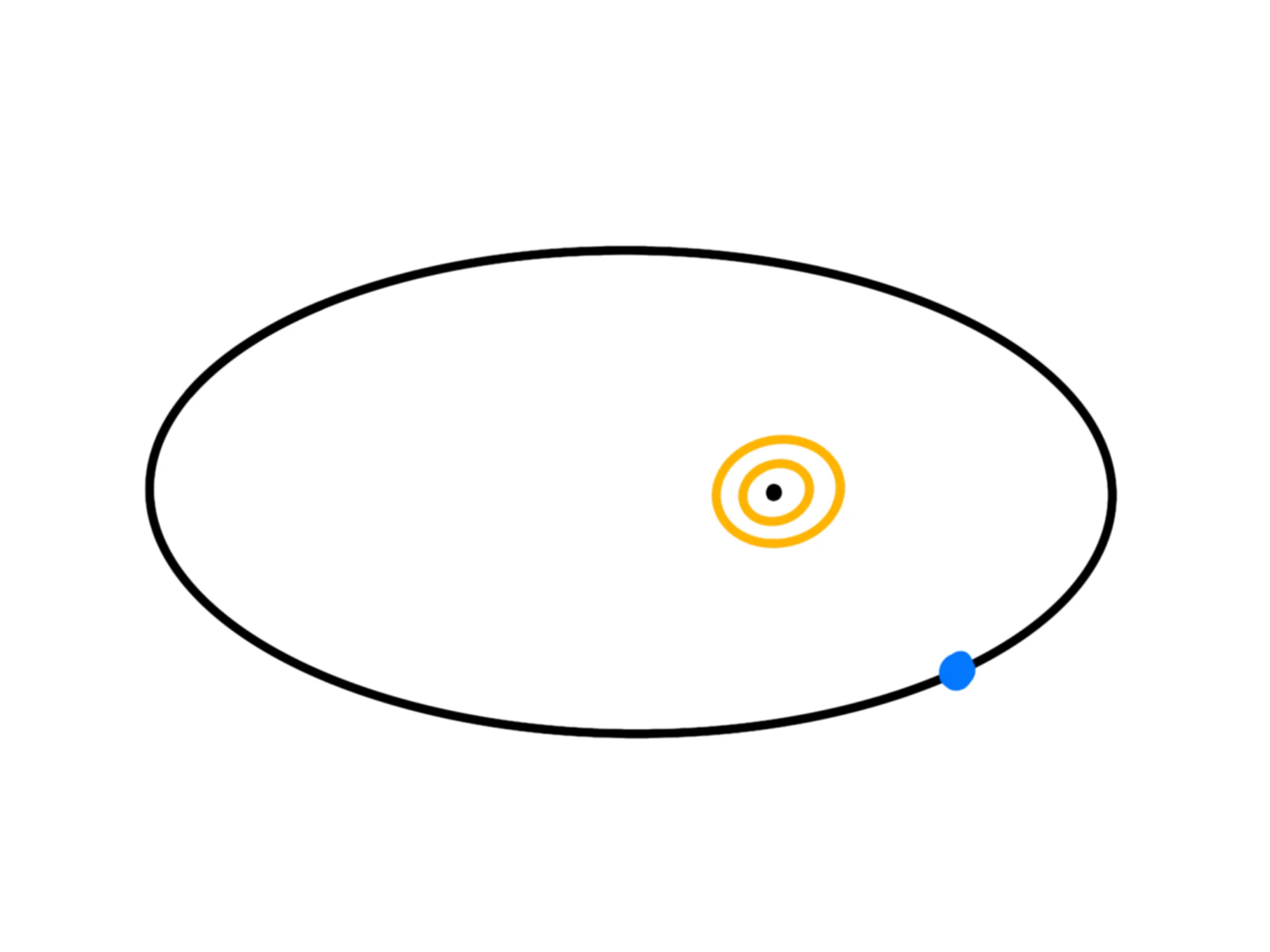
Per prima cosa tracciamo il Sole e il pianeta con la sua orbita ellittica:
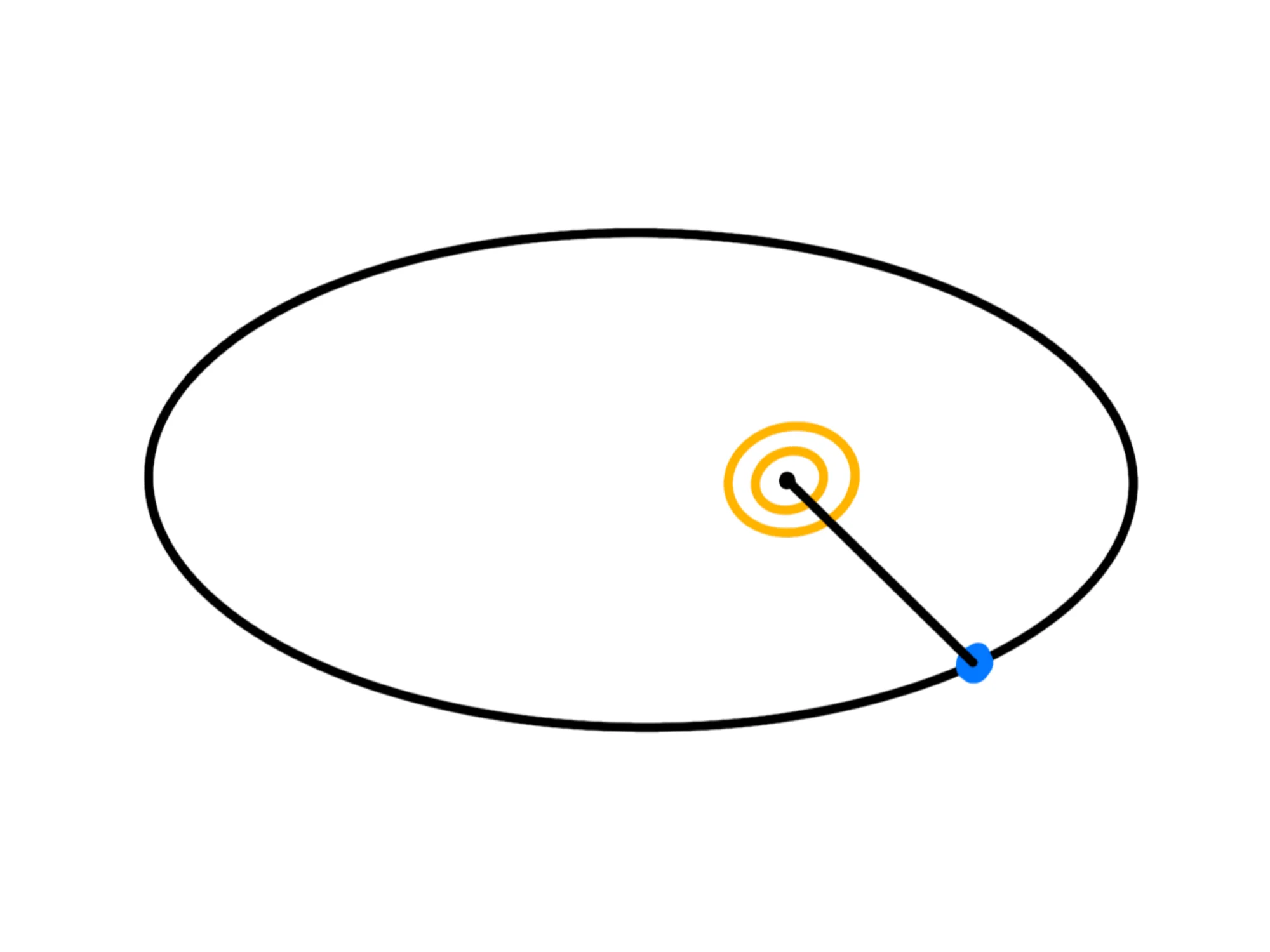
E poi tracciamo il segmento che congiunge i loro due centri:
Quando il pianeta si muoverà intorno al Sole, questo segmento si muoverà e traccerà un'area:
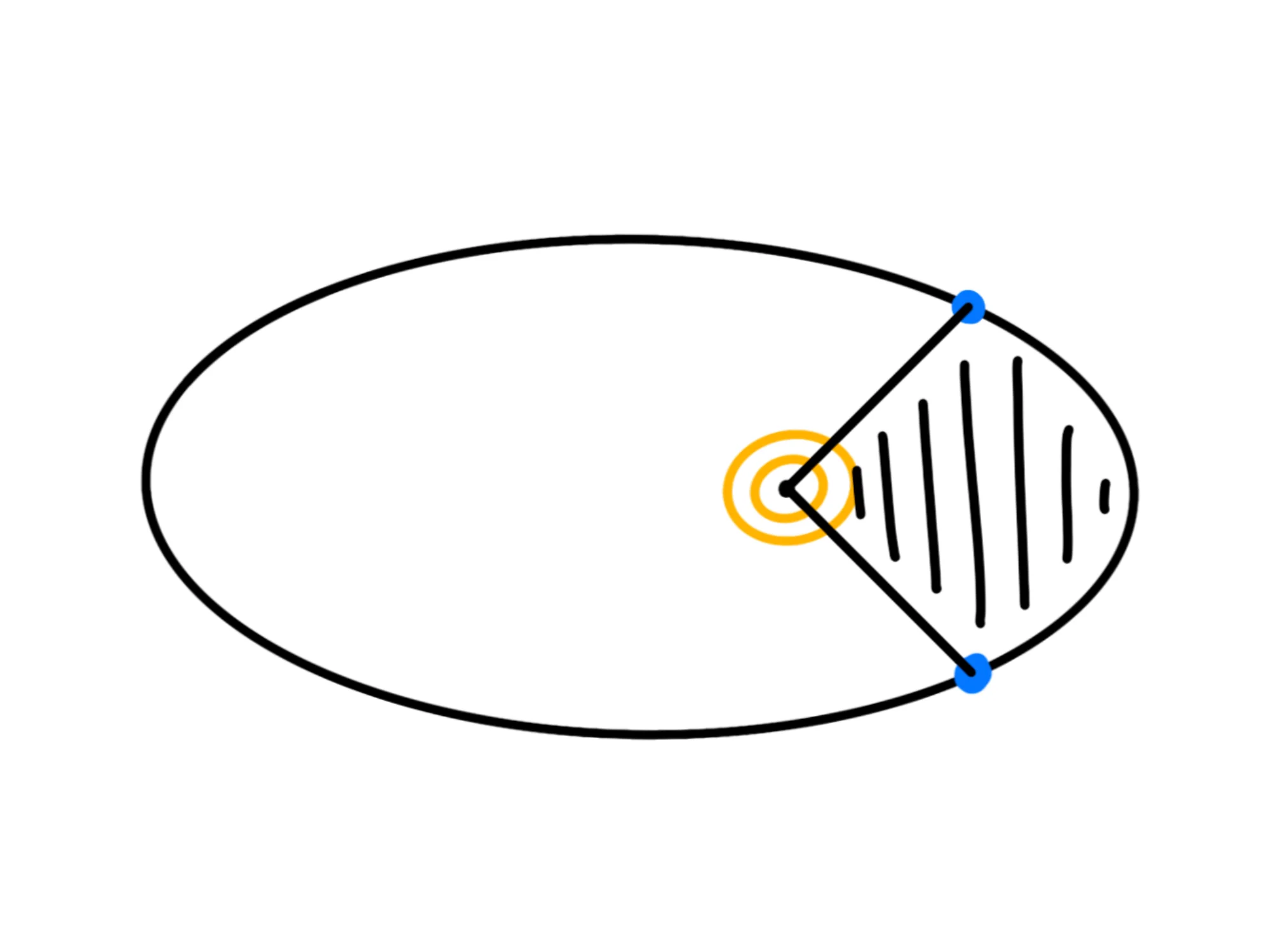
La seconda legge di Keplero ci dice che in tempi uguali, questo segmento traccia sempre aree uguali.
Ciò significa che il pianeta va più veloce quando è vicino al Sole, in modo da compensare la lunghezza minore del segmento, mentre va più lento quando è più lontano:
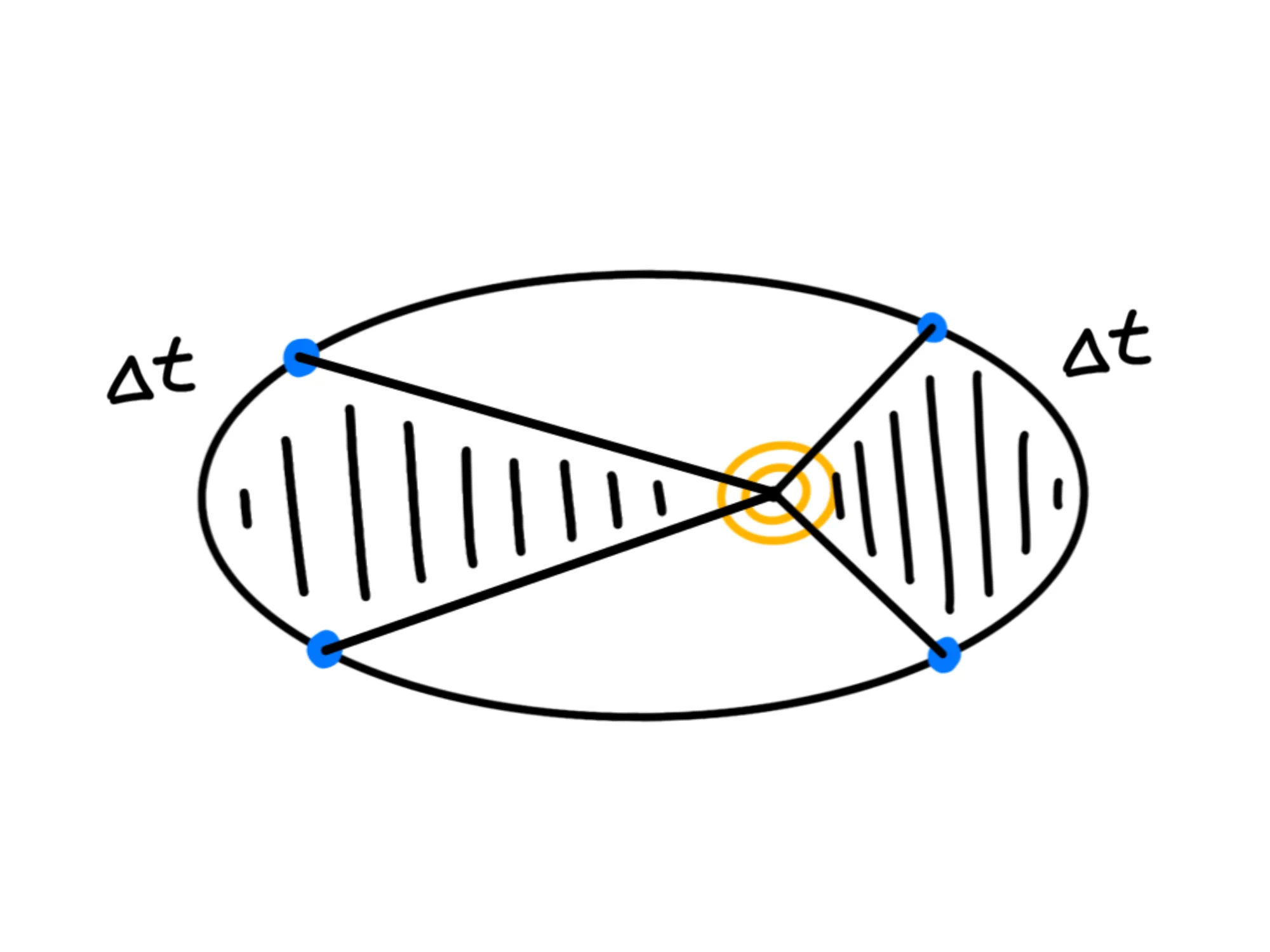
Noi che stiamo sulla Terra non ci sentiamo in continuazione accelerati o rallentati perché, come detto nella scorsa sezione, l'orbita della Terra è un'ellisse molto poco schiacciata, quindi questo cambio di velocità è troppo piccolo e soprattutto avviene troppo lentamente per essere percepito dai nostri sensi.
La terza legge di Keplero ci fornisce una relazione che lega tra loro il tempo impiegato dal pianeta per fare un giro completo intorno al Sole e la distanza tra il pianeta e il Sole.
Infatti afferma che i quadrati dei tempi che i pianeti impiegano a percorrere le loro orbite sono proporzionali al cubo del semiasse maggiore.
Questo tempo impiegato per fare un giro completo viene chiamato periodo e si indica solitamente con la lettera .
Notate che Keplero non parla di "distanza pianeta-Sole", ma di "semiasse maggiore". Cosa intende?
Se vi ricordate, la prima legge di Keplero ci dice che i pianeti non seguono un'orbita circolare ma un'orbita ellittica.
Dunque la distanza tra il pianeta e il Sole varia man mano che il pianeta si muove:
Dunque, quale distanza scegliere? La minima? La massima? La media?
Keplero dimostrò che la distanza corretta da usare affinché la relazione fosse corretta è quella che viene chiamata il semiasse maggiore dell'ellisse.
Quest'ultimo è la distanza tra il centro dell'ellisse e il punto più lontano dell'ellisse:
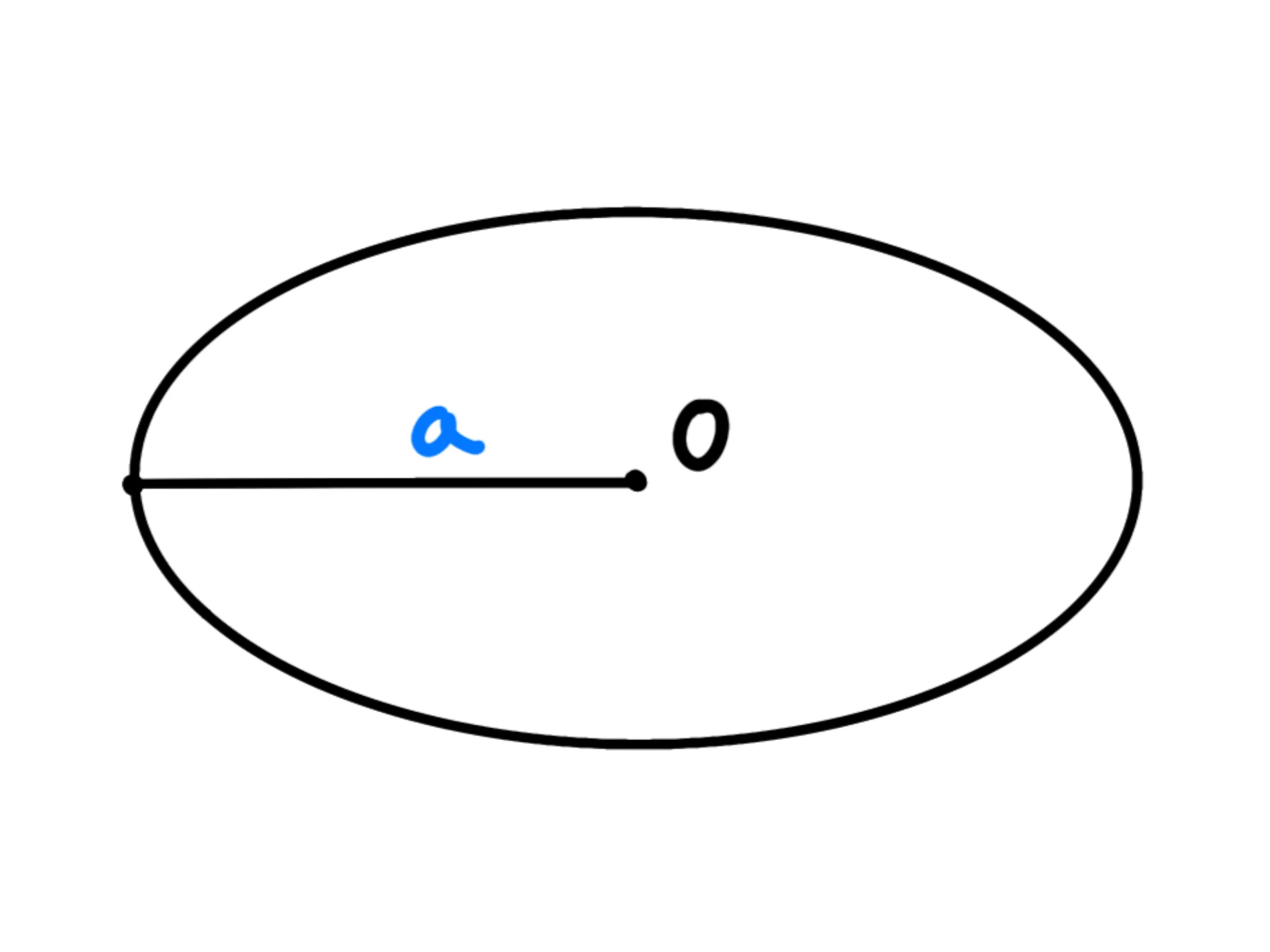
Questa lunghezza viene solitamente chiamata
Dunque, la terza legge di Keplero ci dice che il periodo al quadrato, cioè è direttamente proporzionale al semiasse maggiore al cubo, cioè a
Successivamente, Newton scoprirà che i due sono legati esattamente dall'equazione:
Dove è la costante di gravitazione universale e è la massa della stella.
Concludiamo questa lezione facendo notare che finora abbiamo sempre parlato delle relazioni tra i pianeti e il Sole perché Keplero, vissuto circa nel 1600, poteva studiare solo il Sistema Solare, ma queste leggi sono universali, cioè valgono per qualsiasi pianeta che orbita intorno alla propria stella.