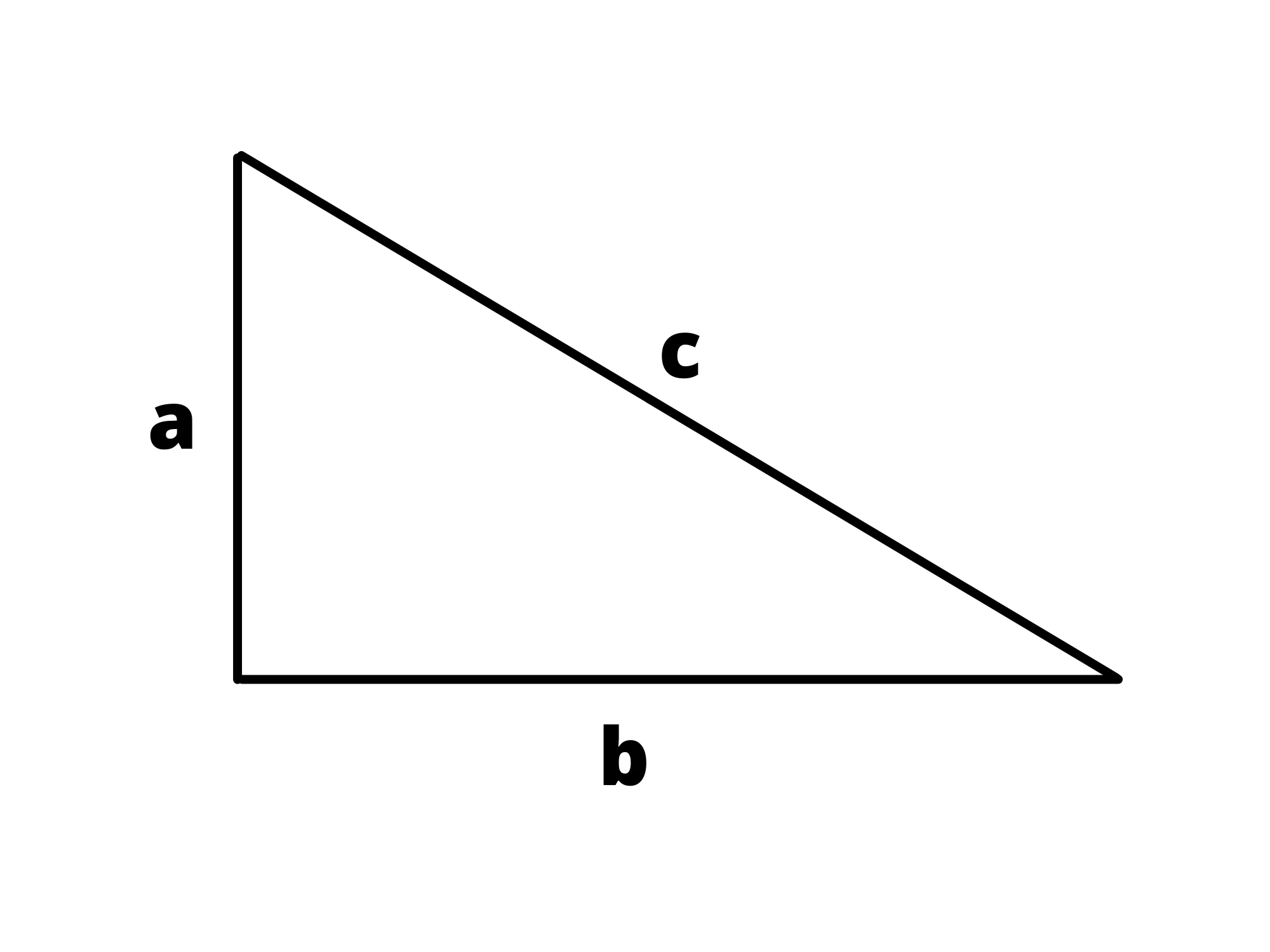
I lati adiacenti all'angolo retto sono detti cateti, mentre quello opposto è detto ipotenusa .

Quindi nel nostro triangolo, $a$ e $b$ sono i cateti, mentre $c$ è l'ipotenusa.

Siccome l'area di un rettangolo è base per altezza, se abbiamo metà rettangolo, l'area del triangolo sarà la metà di essa.

Il cateto $a$ è l'altezza del rettangolo e $b$ è la base, perciò l'area del triangolo sarà:

Cioè cateto per cateto diviso due.

La proprietà più famosa, però, è il teorema di Pitagora, che dice che:

La somma delle aree dei quadrati costruiti sui cateti è uguale all’area del quadrato costruito sull’ipotenusa.

In altre parole, nel triangolo sopra, avremo:

Triangoli rettangoli particolari

Esistono due tipologie di triangoli rettangoli particolari che godono di alcune proprietà aggiuntive che ci permettono di risolvere molti problemi molto più velocemente. Queste due tipologie sono:

1. Il triangolo “ $45^{\circ} - 90 ^{\circ} - 45^{\circ}$”:

Abbiamo detto che un triangolo rettangolo si chiama così perché è la metà di un rettangolo. Se in particolare questo rettangolo è un quadrato, tagliandolo a metà otteniamo un triangolo rettangolo isoscele:

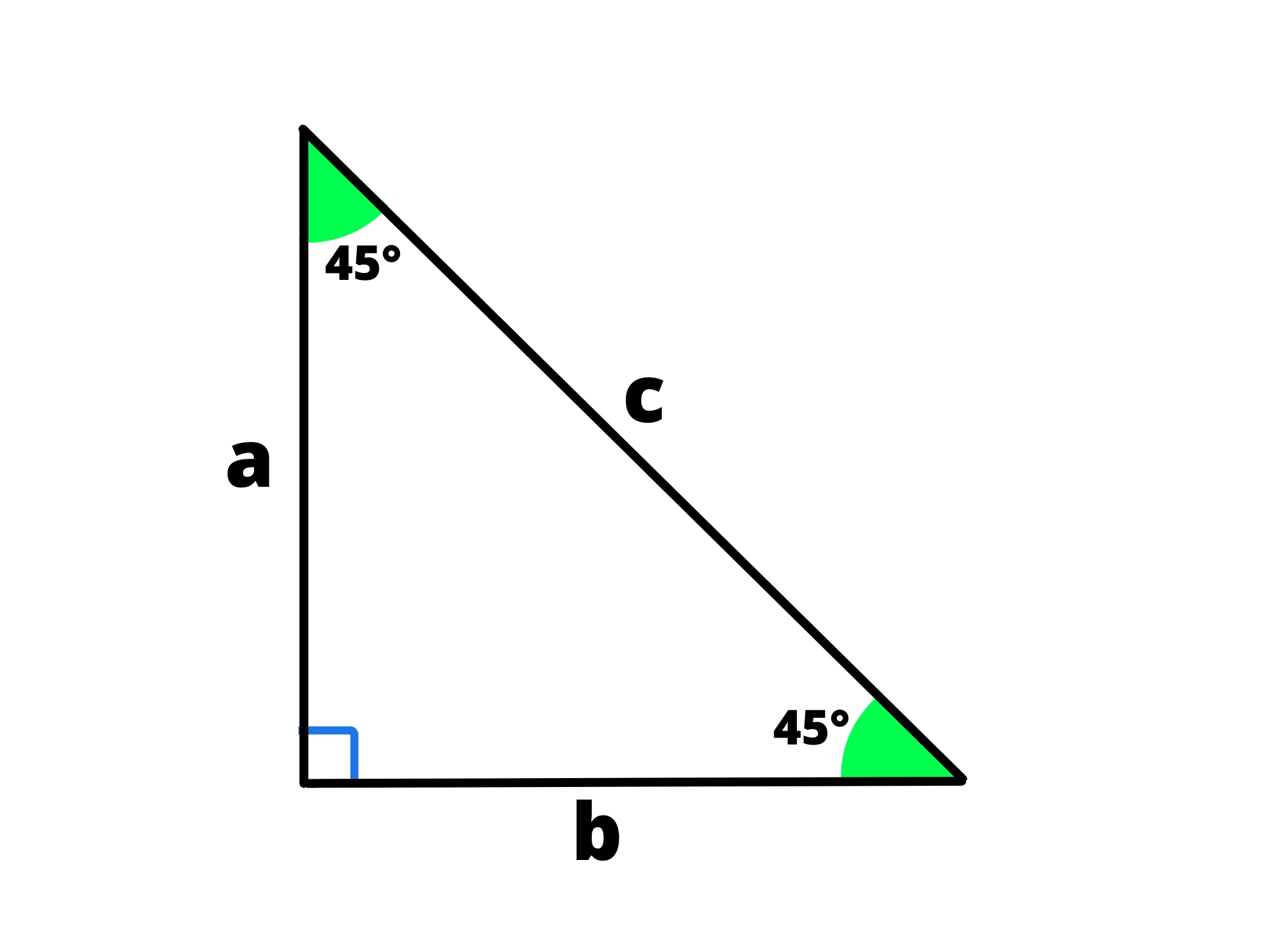
Viene anche chiamato "triangolo $45-90-45$" dal valore dei suoi angoli.

Notiamo che in questo caso cateti del triangolo coincidono con i lati $l$ del quadrato e l'ipotenusa del triangolo coincide con la diagonale $d$ del quadrato:

Possiamo utilizzare il teorema di Pitagora per trovare la diagonale $d$ (che sarebbe l’ipotenusa del triangolo) conoscendo il lato $l$ (che sarebbe il cateto del triangolo):

$l^2 + l^2 = d^2$

$d^2 = 2l^2$

$d=\sqrt{2} l$

2. Il triangolo “ $30^{\circ} – 90^{\circ} – 60^{\circ}$ ”.

Se prendiamo un triangolo equilatero e lo tagliamo a metà, otteniamo il seguente triangolo:

Siccome gli angoli di un triangolo equilatero sono tutti di $60^{\circ}$ e siccome l'altezza è anche bisettrice, gli angoli del triangolo che otteniamo saranno proprio $30^{\circ}, 60^{\circ}$ e $90^{\circ}:$

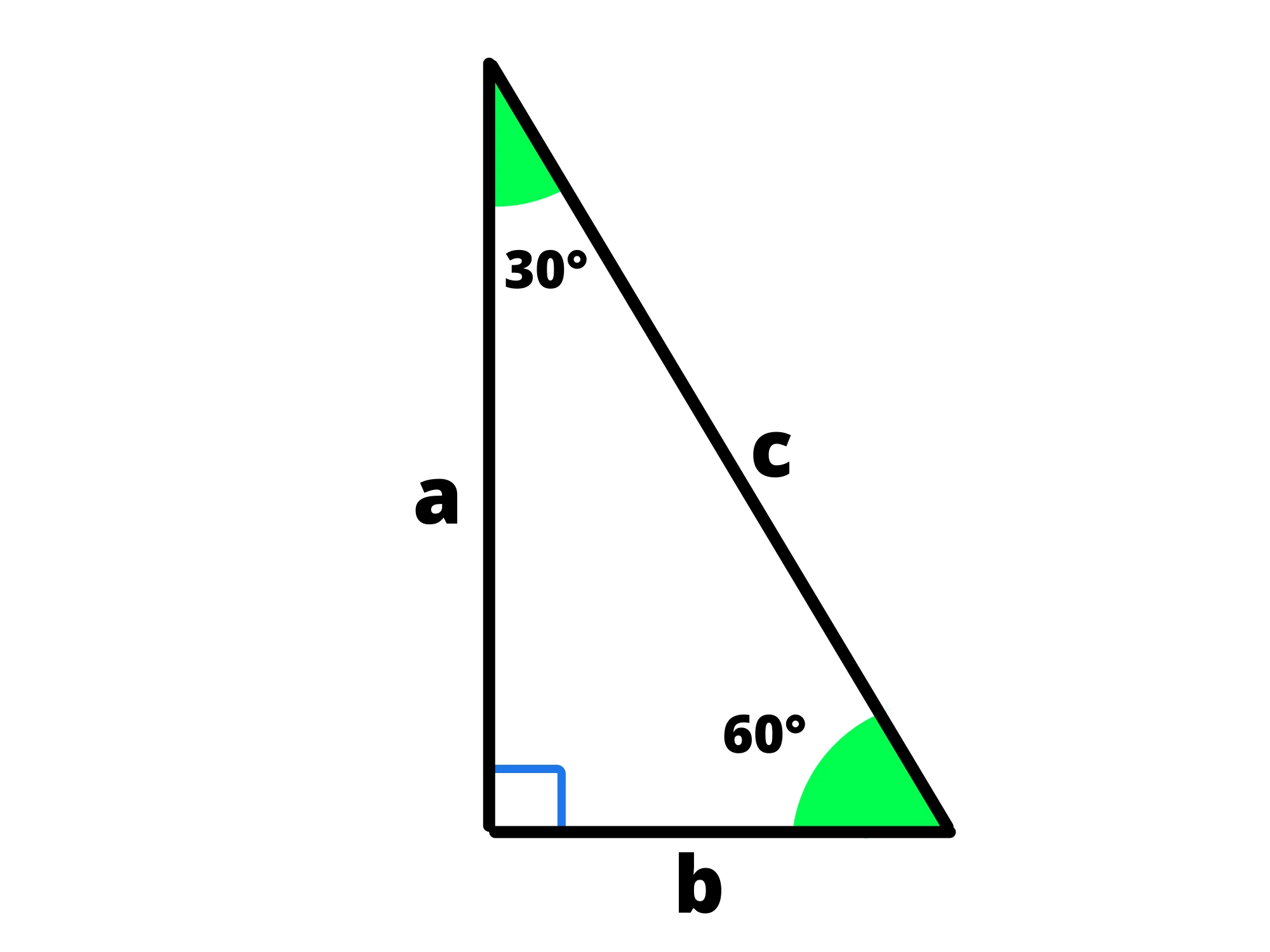
Di conseguenza, utilizzando le proprietà del triangolo equilatero che abbiamo visto prima, avremo:

$b={c\over 2}$

$a={\sqrt{3} \over 2} c$

Utilizzando queste due formule, quindi, possiamo trovare tutti e tre i lati conoscendone uno qualsiasi.