Triangolo equilatero

Un triangolo è detto equilatero se tutti i suoi lati sono uguali. Alternativamente, possiamo dire, come nel caso del triangolo isoscele, che un triangolo è equilatero se tutti i suoi angoli sono uguali.

Anche in questo caso la prima condizione include la seconda e viceversa, quindi potete usare entrambe, anche se è più comune la prima.

Siccome la somma degli angoli interni di un triangolo è sempre $180^{\circ}$ e tutti e tre gli angoli sono uguali, allora ognuno di loro deve essere uguale a un terzo di $180^{\circ},$ ovvero $60^{\circ}.$

Dunque, gli angoli interni di un triangolo equilatero sono sempre di $60^{\circ}.$

Il triangolo equilatero è un caso particolare di triangolo isoscele in cui anche la base è uguale al lato obliquo.

Di conseguenza, tutte le sue altezze sono anche mediane e bisettrici:

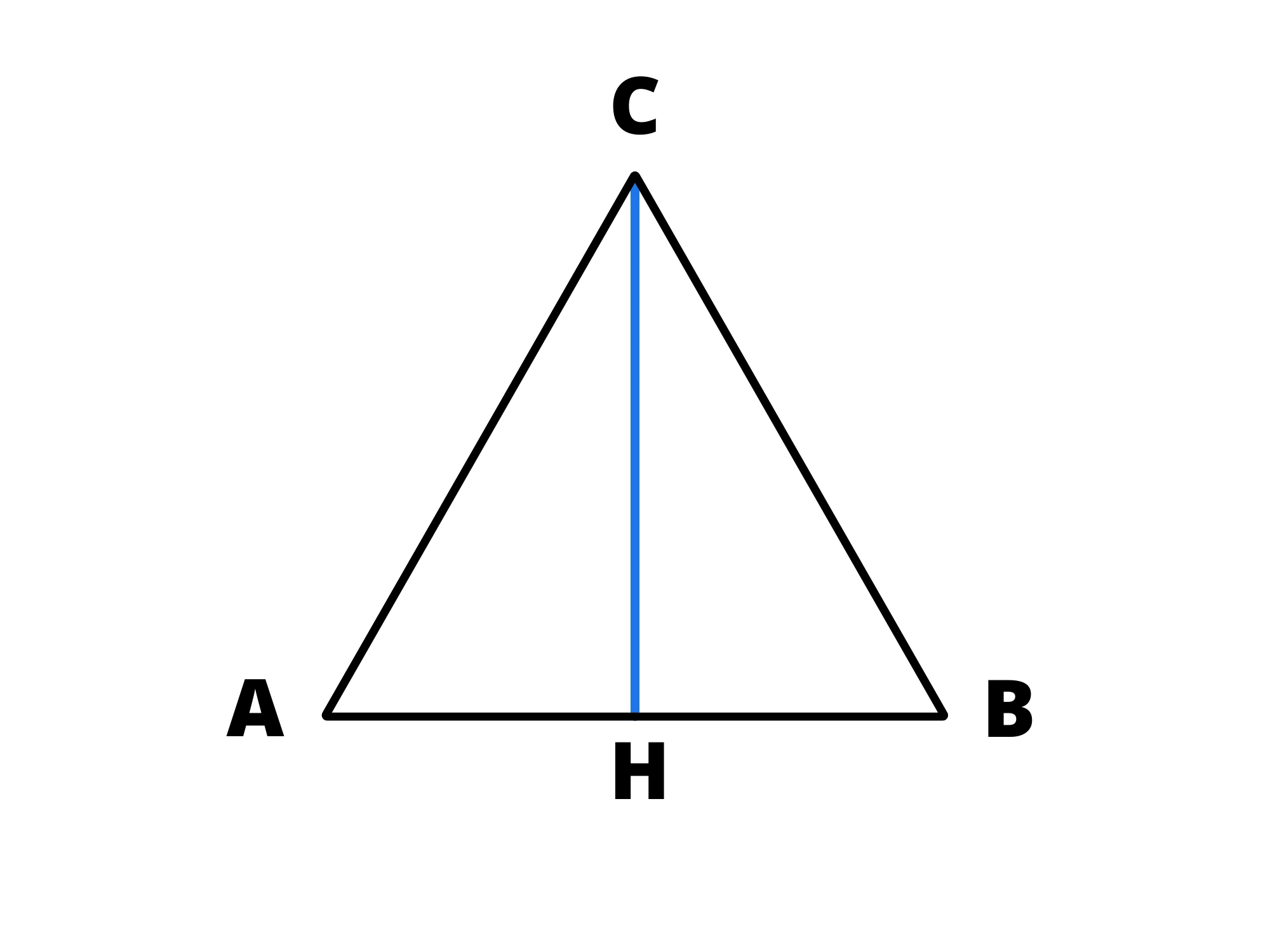
Tracciando l’altezza da uno dei vertici, per questa proprietà dobbiamo avere:

$AH = HB$

Siccome abbiamo inoltre che:

$AH+HB=AB$

Otteniamo che:

$AH+AH=AB$

$AH={AB \over 2}$

Possiamo quindi applicare il teorema di Pitagora nel triangolo rettangolo $\overset{\Delta}{AHC}$ per trovare l’altezza $h$ ( che sarebbe $CH$ ) in funzione del lato $l$ ( che sarebbe $AB$ ). Avremo quindi:

$AH^2 + CH^2 = CA^2$

$({AB\over 2})^2 + CH^2 = AB^2$

${l\over 2}^2 +h^2 = l^2$

$h^2 = l^2 – {l^2 \over 4}$

$h^2= {4l^2 –l^2 \over 4}$

$h= \sqrt{3l^2 \over 4}$

Dunque possiamo usare questa formula per trovare l'altezza di un triangolo equilatero conoscendo il suo lato e viceversa.