Cosa sono i triangoli particolari?

Esistono dei casi particolari di triangoli che godono di alcune proprietà. Conoscerle ci permette di risolvere molto più facilmente alcuni problemi.

Triangolo rettangolo

Un triangolo è detto rettangolo se uno dei suoi angoli è un angolo retto. Si chiama così perché è metà di un rettangolo:

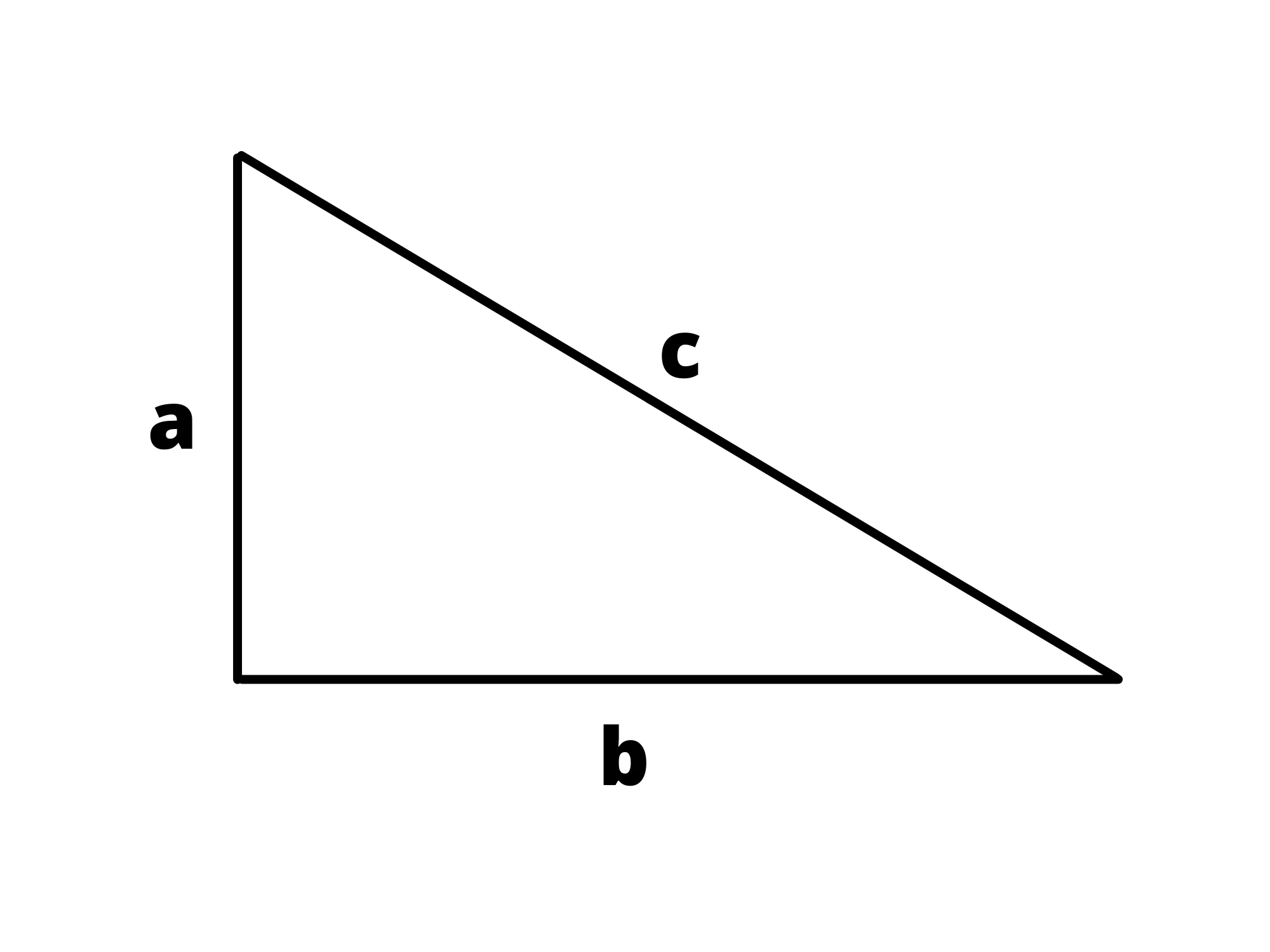
I lati adiacenti all'angolo retto sono detti cateti, mentre quello opposto è detto ipotenusa .

Quindi nel nostro triangolo, $a$ e $b$ sono i cateti, mentre $c$ è l'ipotenusa.

Siccome l'area di un rettangolo è base per altezza, se abbiamo metà rettangolo, l'area del triangolo sarà la metà di essa.

Il cateto $a$ è l'altezza del rettangolo e $b$ è la base, perciò l'area del triangolo sarà:

Cioè cateto per cateto diviso due.

La proprietà più famosa, però, è il teorema di Pitagora, che dice che:

La somma delle aree dei quadrati costruiti sui cateti è uguale all’area del quadrato costruito sull’ipotenusa.

In altre parole, nel triangolo sopra, avremo:

Triangolo isoscele

Un triangolo è detto isoscele se ha due lati uguali. I due lati uguali vengono chiamati “lati obliqui” mentre il terzo si chiama “base”.

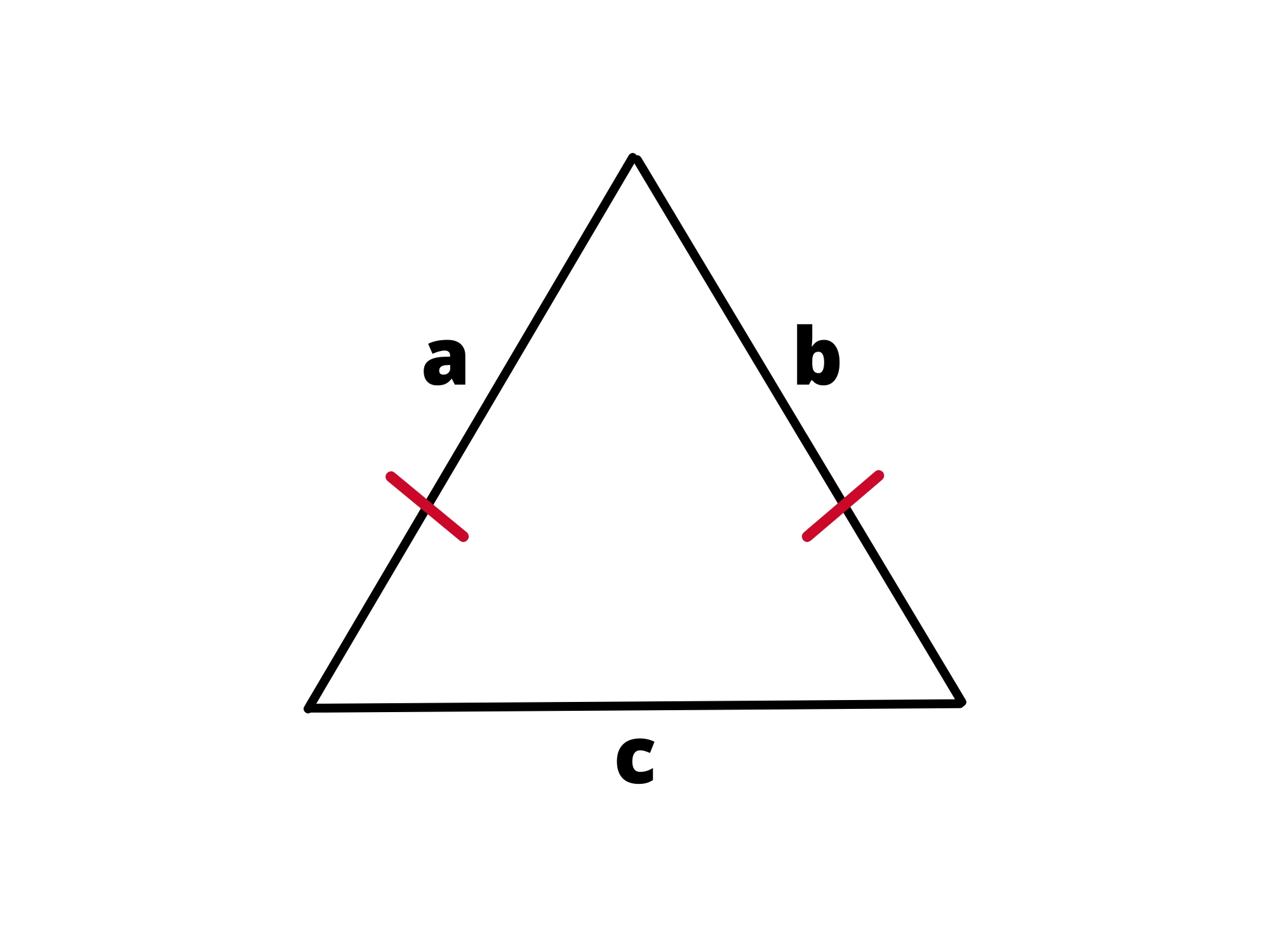
Alternativamente, si può anche definire un triangolo isoscele come un triangolo con due angoli uguali. Siccome la prima condizione comporta la seconda e viceversa, potete usare entrambe.

Il triangolo isoscele gode di una proprietà interessante:

L’altezza della base è anche uguale alla mediana e alla bisettrice dell’angolo opposto:

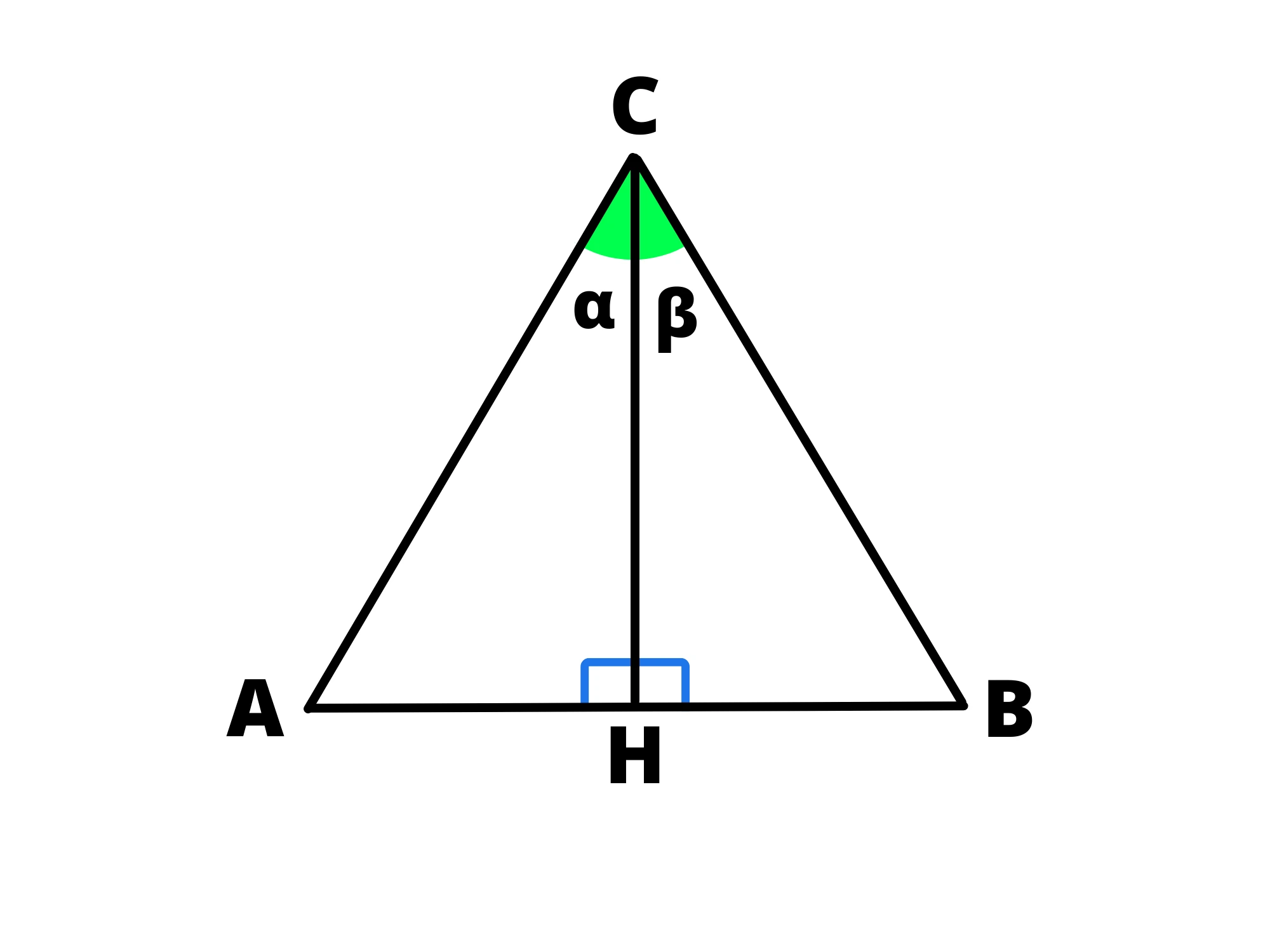
Avremo quindi che data una delle tre seguenti condizioni:

• $\widehat{A H C} = 90^{\circ}$ (o $\widehat{BHC} = 90^{\circ}$ )
• $AH=HB$
• $\alpha = \beta$

Allora anche le altre due devono essere vere.

Triangolo equilatero

Un triangolo è detto equilatero se tutti i suoi lati sono uguali. Alternativamente, possiamo dire, come nel caso del triangolo isoscele, che un triangolo è equilatero se tutti i suoi angoli sono uguali.

Anche in questo caso la prima condizione include la seconda e viceversa, quindi potete usare entrambe, anche se è più comune la prima.

Siccome la somma degli angoli interni di un triangolo è sempre $180^{\circ}$ e tutti e tre gli angoli sono uguali, allora ognuno di loro deve essere uguale a un terzo di $180^{\circ},$ ovvero $60^{\circ}.$

Dunque, gli angoli interni di un triangolo equilatero sono sempre di $60^{\circ}.$

Il triangolo equilatero è un caso particolare di triangolo isoscele in cui anche la base è uguale al lato obliquo.

Di conseguenza, tutte le sue altezze sono anche mediane e bisettrici:

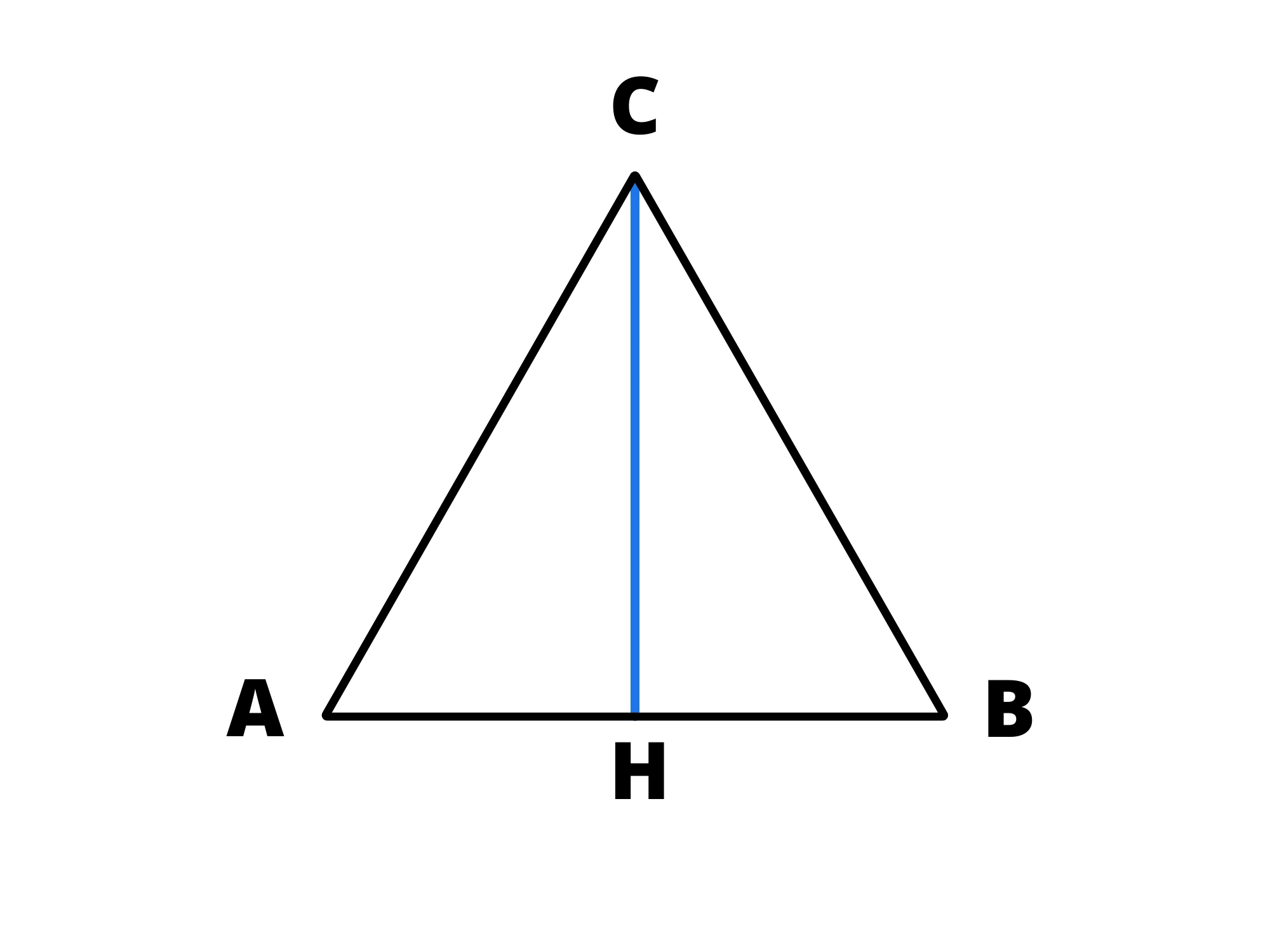
Tracciando l’altezza da uno dei vertici, per questa proprietà dobbiamo avere:

$AH = HB$

Siccome abbiamo inoltre che:

$AH+HB=AB$

Otteniamo che:

$AH+AH=AB$

$AH={AB \over 2}$

Possiamo quindi applicare il teorema di Pitagora nel triangolo rettangolo $\overset{\Delta}{AHC}$ per trovare l’altezza $h$ ( che sarebbe $CH$ ) in funzione del lato $l$ ( che sarebbe $AB$ ). Avremo quindi:

$AH^2 + CH^2 = CA^2$

$({AB\over 2})^2 + CH^2 = AB^2$

${l\over 2}^2 +h^2 = l^2$

$h^2 = l^2 – {l^2 \over 4}$

$h^2= {4l^2 –l^2 \over 4}$

$h= \sqrt{3l^2 \over 4}$

Dunque possiamo usare questa formula per trovare l'altezza di un triangolo equilatero conoscendo il suo lato e viceversa.

Triangoli rettangoli particolari

Esistono due tipologie di triangoli rettangoli particolari che godono di alcune proprietà aggiuntive che ci permettono di risolvere molti problemi molto più velocemente. Queste due tipologie sono:

1. Il triangolo “ $45^{\circ} - 90 ^{\circ} - 45^{\circ}$”:

Abbiamo detto che un triangolo rettangolo si chiama così perché è la metà di un rettangolo. Se in particolare questo rettangolo è un quadrato, tagliandolo a metà otteniamo un triangolo rettangolo isoscele:

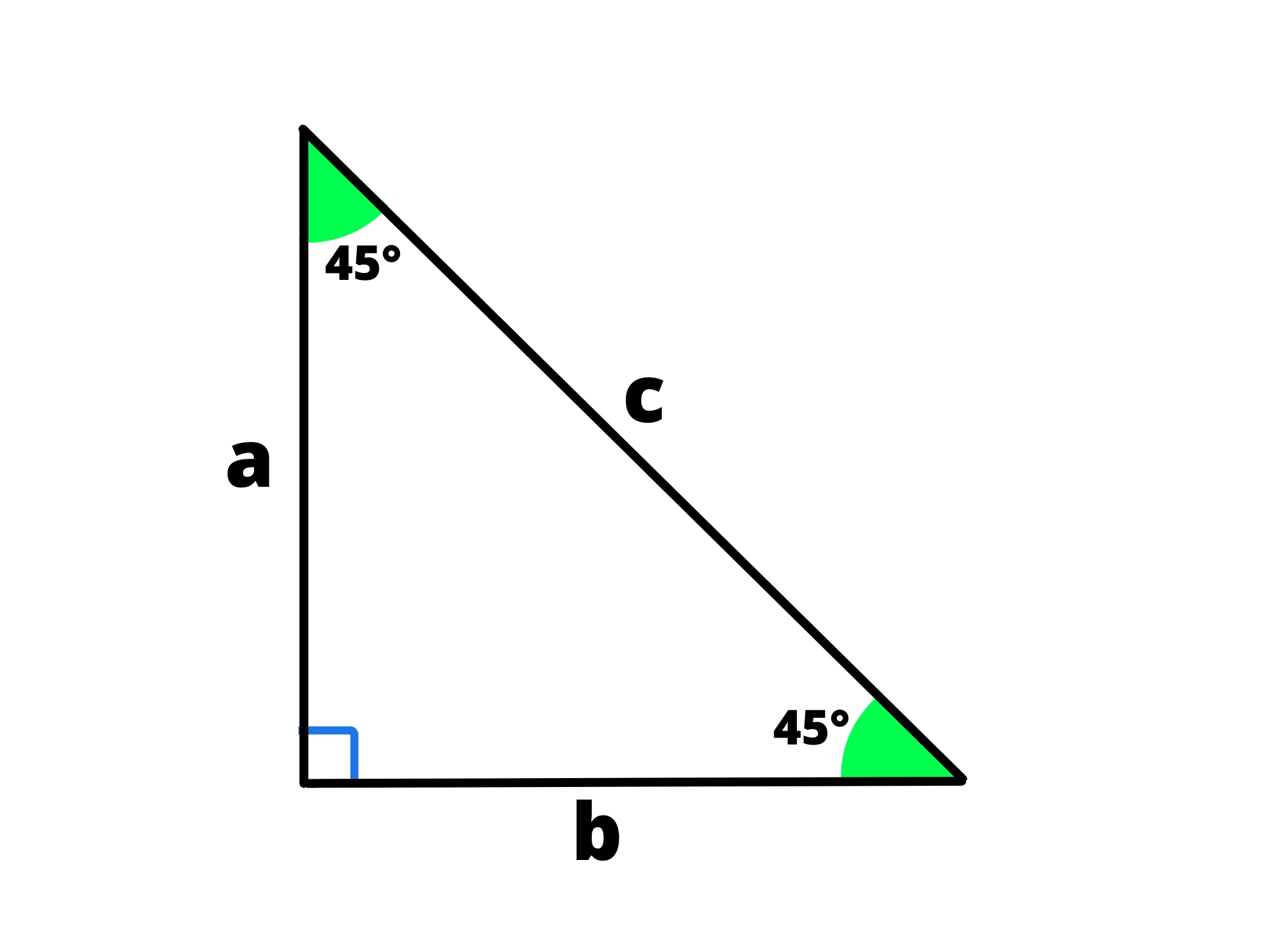
Viene anche chiamato "triangolo $45-90-45$" dal valore dei suoi angoli.

Notiamo che in questo caso cateti del triangolo coincidono con i lati $l$ del quadrato e l'ipotenusa del triangolo coincide con la diagonale $d$ del quadrato:

Possiamo utilizzare il teorema di Pitagora per trovare la diagonale $d$ (che sarebbe l’ipotenusa del triangolo) conoscendo il lato $l$ (che sarebbe il cateto del triangolo):

$l^2 + l^2 = d^2$

$d^2 = 2l^2$

$d=\sqrt{2} l$

2. Il triangolo “ $30^{\circ} – 90^{\circ} – 60^{\circ}$ ”.

Se prendiamo un triangolo equilatero e lo tagliamo a metà, otteniamo il seguente triangolo:

Siccome gli angoli di un triangolo equilatero sono tutti di $60^{\circ}$ e siccome l'altezza è anche bisettrice, gli angoli del triangolo che otteniamo saranno proprio $30^{\circ}, 60^{\circ}$ e $90^{\circ}:$

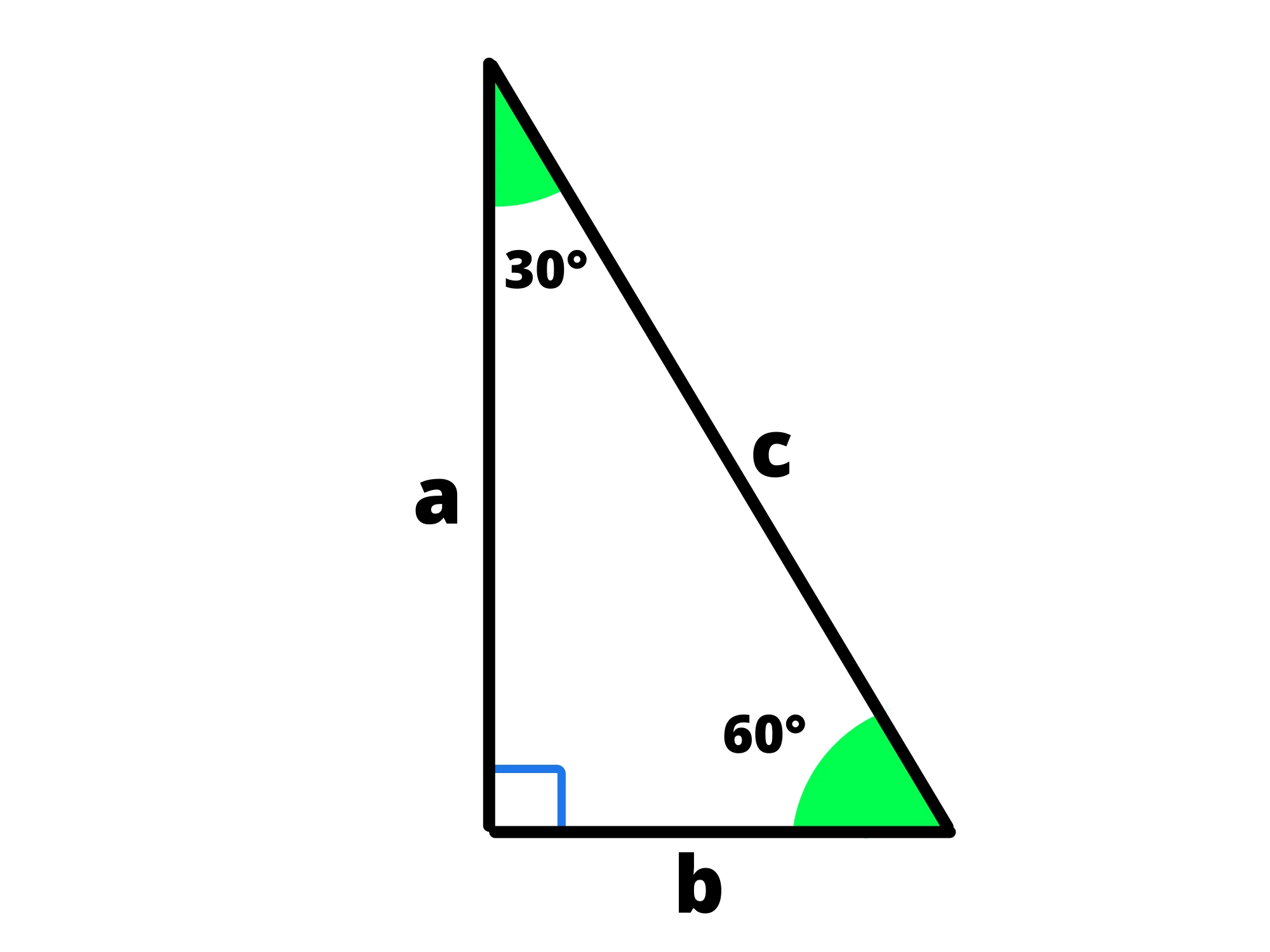
Di conseguenza, utilizzando le proprietà del triangolo equilatero che abbiamo visto prima, avremo:

$b={c\over 2}$

$a={\sqrt{3} \over 2} c$

Utilizzando queste due formule, quindi, possiamo trovare tutti e tre i lati conoscendone uno qualsiasi.