Cosa sono le trasformazioni termodinamiche?

Le trasformazioni termodinamiche sono dei processi in cui un sistema passa da uno stato di equilibrio a un altro.

Quindi, ad esempio, se metti del gas in un palloncino, raffreddi il palloncino e il gas raggiunge l'equilibrio, hai effettuato una trasformazione termodinamica.

Solitamente raffiguriamo una trasformazione termodinamica riportando lo stato del gas in un piano $V-p$ (cioè volume-pressione), come faremo nel corso di questa lezione.

I casi particolari di trasformazioni termodinamiche che studieremo sono quelle: isobare, isocore, isoterme e adiabatiche.

Trasmormazione isobara

Una trasformazione termodinamica è detta isobara se la pressione rimane costante.

Infatti il prefisso iso- vuole dire "stessa" e -bara sta per "pressione".

Prendiamo l'equazione di stato dei gas perfetti che ci dice che:

$pV = nRT$

Da questa ricaviamo che:

Tutte le grandezze a destra dell'uguale rimangono costanti durante la trasformazione, quindi anche ${V\over T}$ sarà uguale ad una costante. Questo significa che il volume e la temperatura sono direttamente proporzionali.

Infatti la prima legge di Gay-Lussac afferma che:

Per ogni determinata quantità di sostanza e a pressione costante, il volume di un gas è direttamente proporzionale alla sua temperatura assoluta.

Ricordatevi infatti di prendere la temperatura in gradi Kelvin, non in Celsius.

Nel piano $V-p,$ siccome la pressione è appunto costante, la trasformazione sarà rappresentata da un tratto orizzontale:

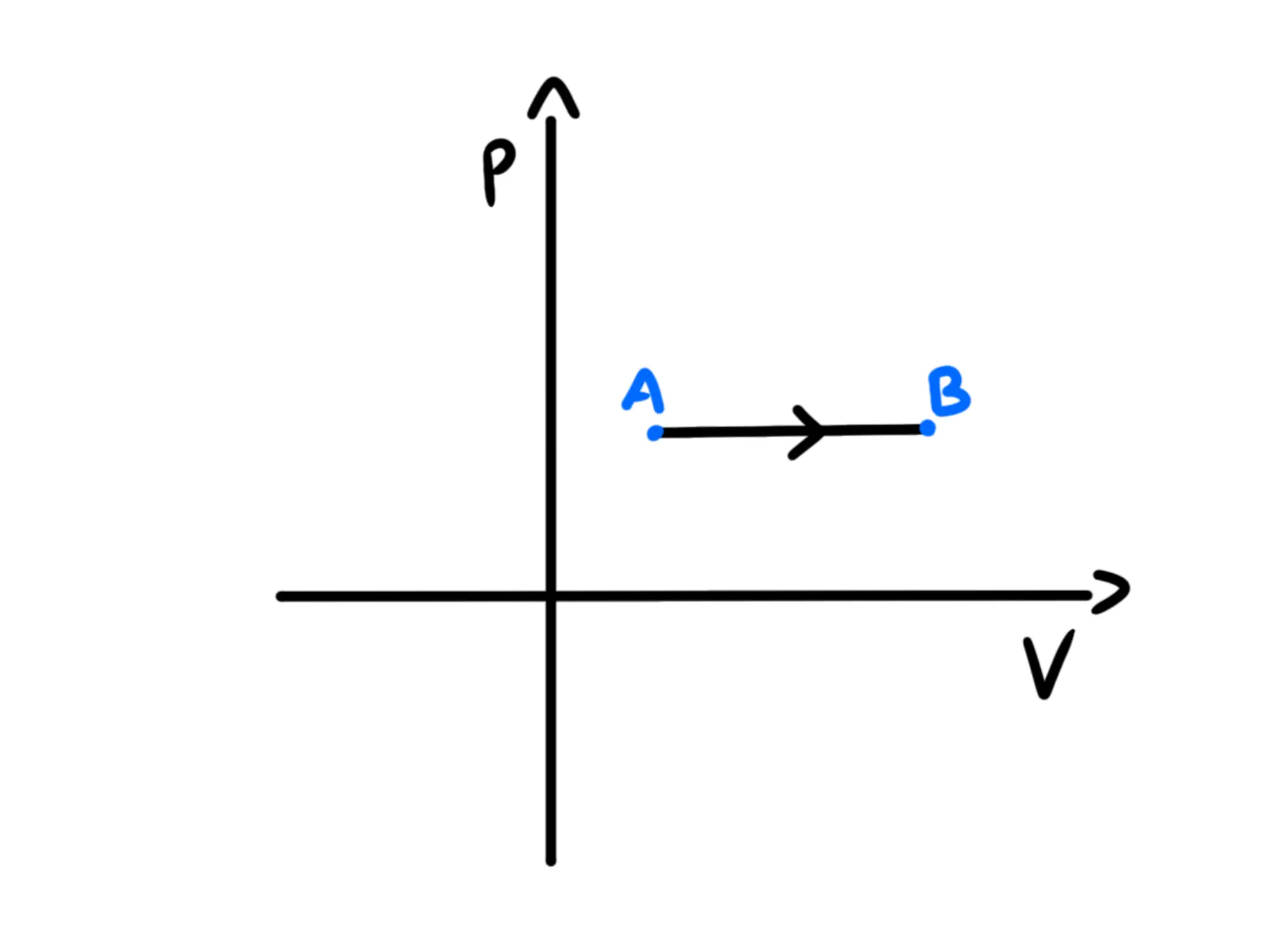
Ricordatevi sempre di mettere il verso della trasformazione. Dovete mettere una freccetta per indicare se avviene da $A$ a $B$ (come nel nostro grafico) o da $B$ ad $A.$

Trasformazione isocora

Una trasformazione termodinamica è detta isocora se il volume viene mantenuto costante.

Infatti il prefisso "iso-" vuol dire "stesso" in greco antico e "cora" viene da "khora", "volume" in greco antico.

L'equazione di stato dei gas ci dice che:

$pV = nRT$

Da cui ricaviamo:

Tutte le grandezze a destra dell'uguale sono costanti e questo significa che anche la parte a sinistra dovrà essere costante. Quindi in una trasformazione isocora il rapporto tra la pressione e la temperatura è costante, cioè sono direttamente proporzionali.

Questo è, infatti, quanto annuncia la seconda legge di Gay-Lussac:

Per ogni determinata quantità di sostanza e a volume costante, la pressione di un gas è direttamente proporzionale alla sua temperatura assoluta.

Nel piano $V-p$ una trasformazione isocora, essendo il volume costante, sarà uguale ad un tratto verticale:

Trasmormazione isoterma

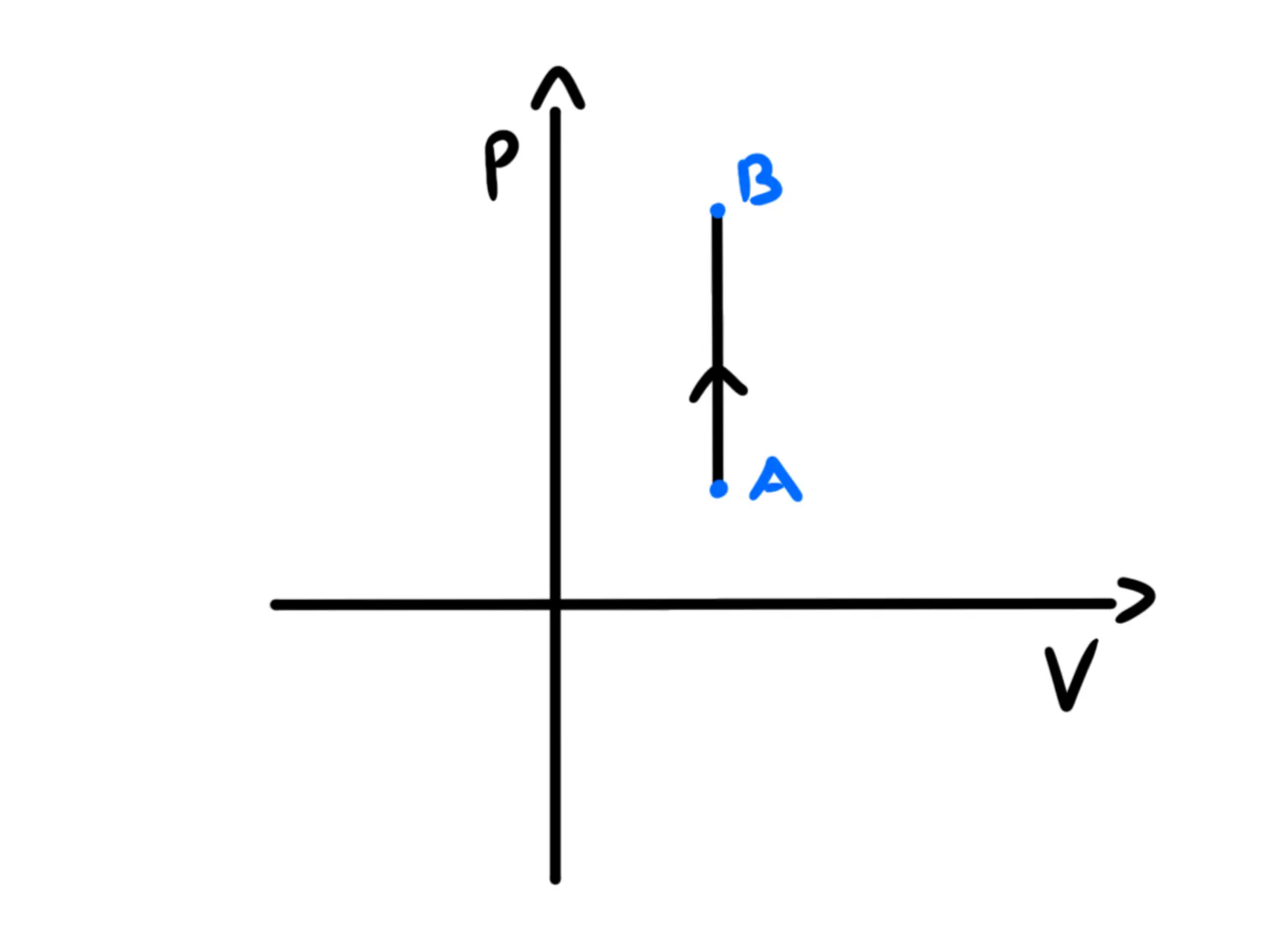
Una trasformazione termodinamica è detta isoterma se la temperatura viene mantenuta costante.

Prendiamo come prima la legge di stato dei gas:

Tutti i termini a destra dell'uguale sono costanti, quindi anche $pV$ sarà costante. Questo significa che la pressione e il volume sono indirettamente proporzionali.

Infatti la legge di Boyle afferma che:

A temperatura costante, il volume di una massa di gas è inversamente proporzionale alla pressione esercitata sul gas

Nel piano $V-p$ otterremmo una curva del tipo $pV = k,$ dove $k$ è appunto una costante.

Riscrivendola come $p = {k\over V},$ notiamo che si tratta dell'equazione di un'iperbole. Quindi la trasformazione apparirà come la seguente:

Trasformazione adiabatica

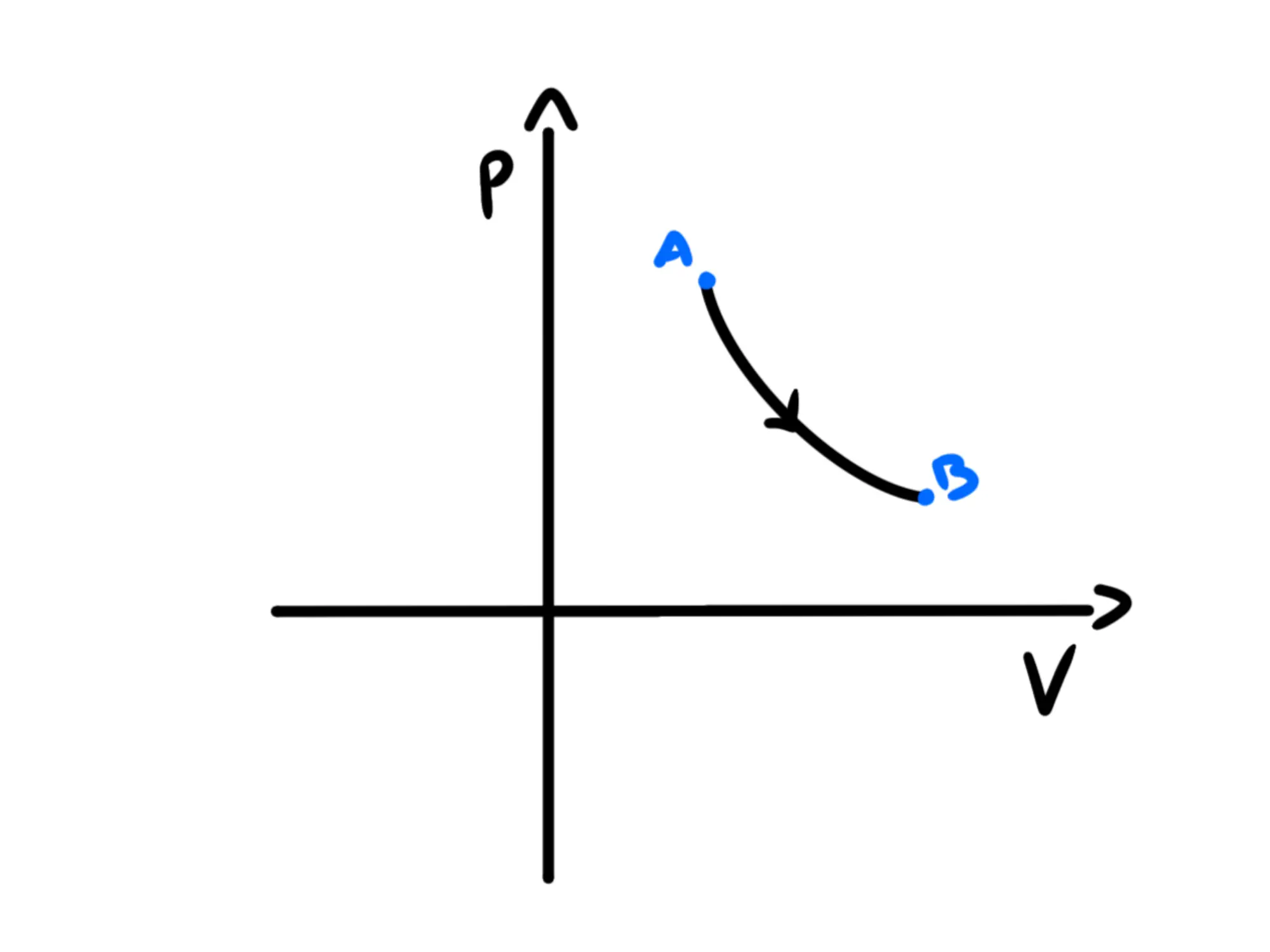
Una trasformazione termodinamica è detta adiabatica se non viene scambiato calore con l'ambiente esterno.

Il lavoro e il calore delle trasformazioni termodinamiche

Durante una trasformazione termodinamica, può esserci uno scambio di calore con l'ambiente esterno e il nostro gas può fare lavoro o può essere fatto lavoro sul gas.

Per esempio, se stiamo riscaldando un cilindro con sopra un pistone, stiamo dando calore al gas e quest'ultimo, espandendosi, alzerà il pistone, compiendo dunque un lavoro.

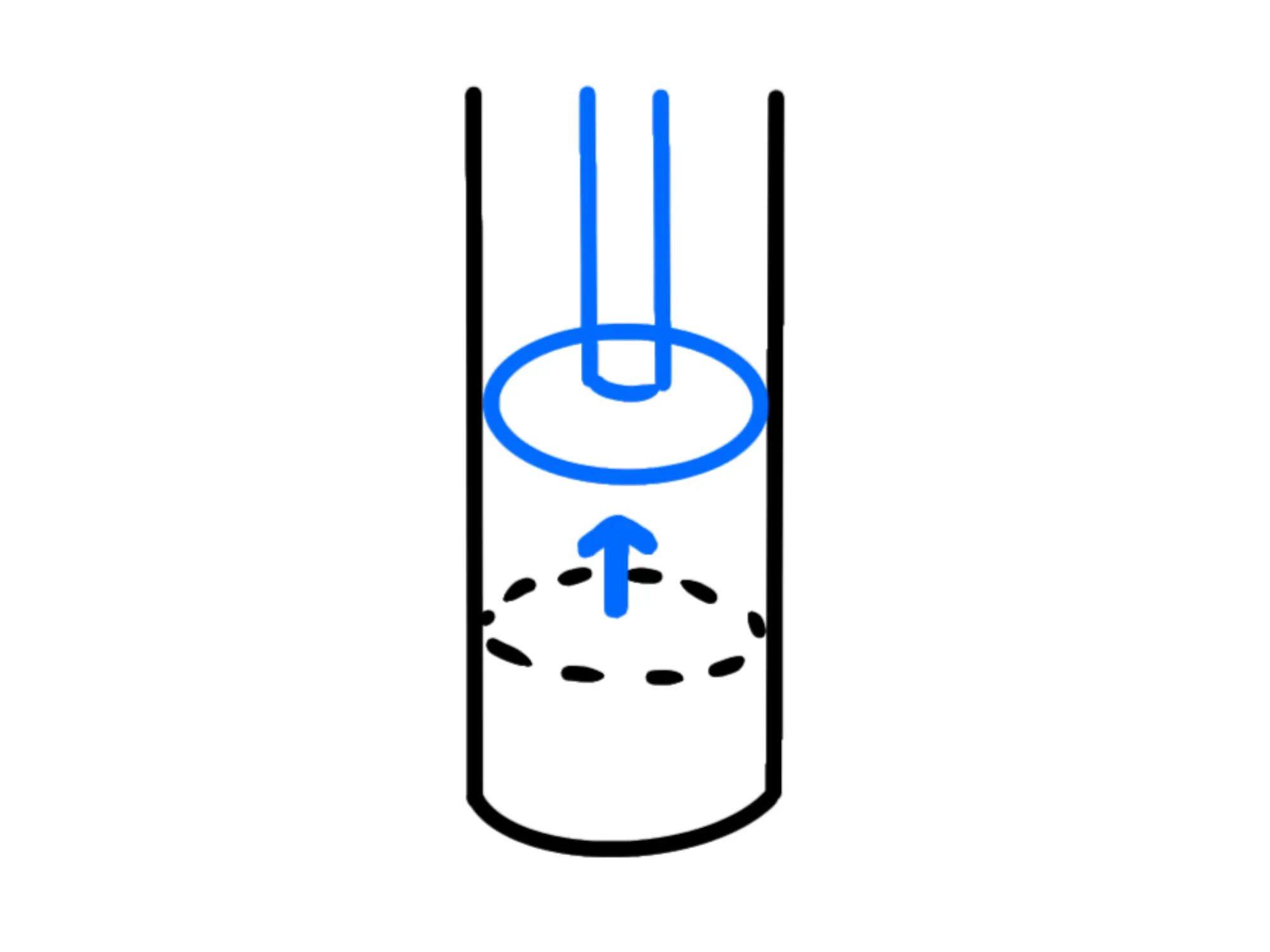
Se invece spingiamo giù noi il pistone, comprimendo il gas, siamo noi che stiamo facendo lavoro sul gas.

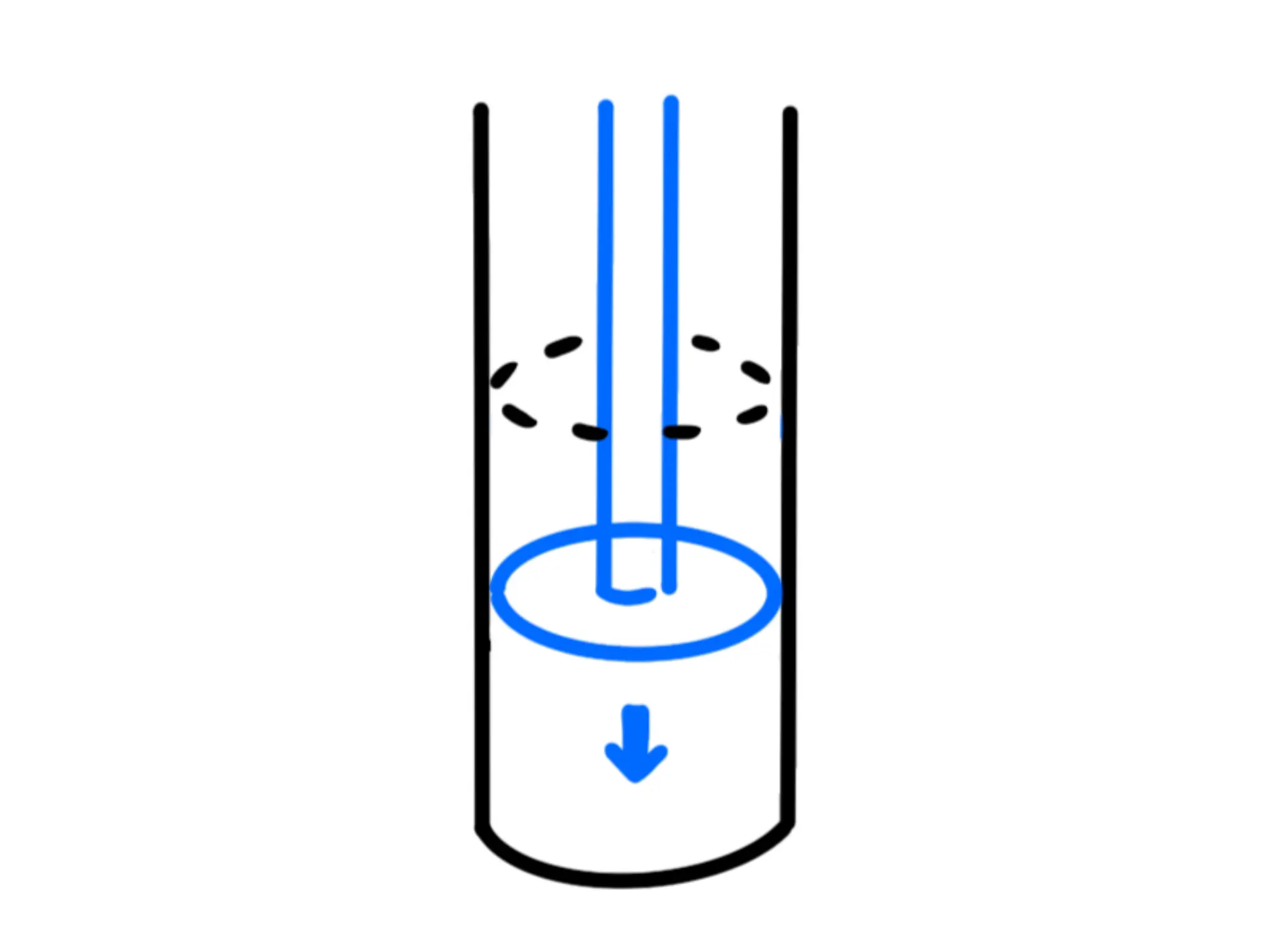
Bisogna decidersi su quale segno dare a questi lavori e calori. Per convenzione, si è deciso che il lavoro fatto dal gas è positivo, mentre quello fatto sul gas è negativo.

Per il calore si è deciso il contrario: il calore acquisito dal gas è positivo, mentre il calore ceduto dal gas è negativo.

Con questi segni, possiamo riscrivere la seconda legge della termodinamica come:

Dove ricordiamo che $Q$ sta per il calore, $L$ sta per il lavoro e $\Delta U$ sta per la variazione di energia interna (che si calcola come $c_v n \Delta T$ ).

Molto spesso ci interessa quanto lavoro fa una trasformazione, in modo da poterlo usare per compiere azioni, che può essere muovere un treno o anche far funzione la tua macchina del caffè.

Si può dimostrare che il lavoro fatto da una trasformazione è anche uguale a $p\Delta V.$ Adesso lo dimostreremo nel caso particolare di un pistone che si espande:

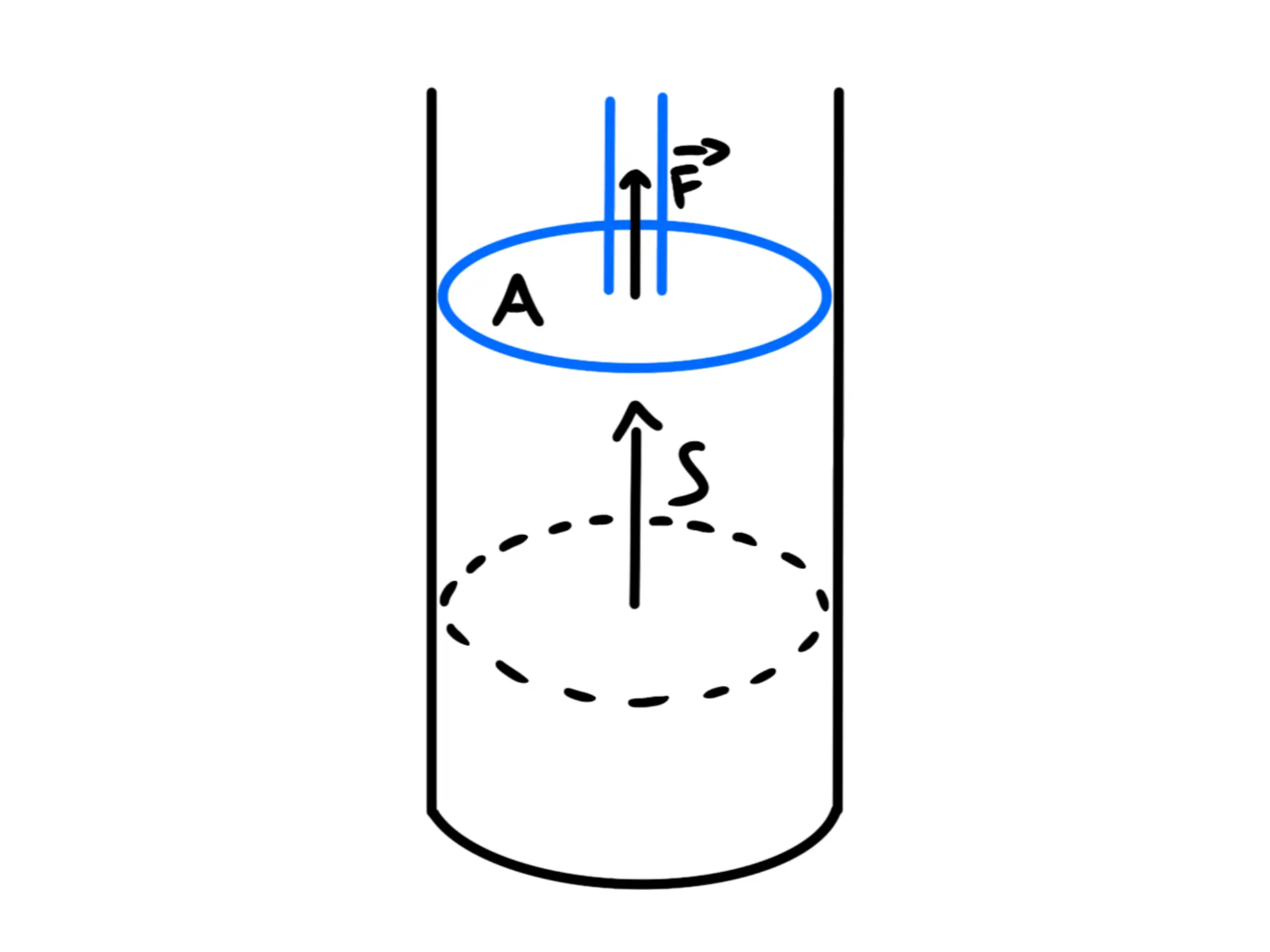
Il lavoro fatto dal gas sul pistone di calcola come $\overrightarrow{F} \cdot \overrightarrow{s}.$ Siccome questi due vettori sono paralleli, il prodotto scalare sarà uguale al prodotto dei moduli, cioè a $Fs.$

Possiamo moltiplicare e dividere per l'area $A$ della faccia del pistone che viene spinta, ottenendo:

$L = Fs \cdot {A\over A}$

Questo possiamo riscriverlo come:

$L = {F\over A} \cdot sA$

$F\over A$ sarebbe forza fratto superficie, cioè la pressione $p,$ mentre $sA$ è uguale al volume spostato dal gas, cioè a quanto volume in più adesso occupa, ovvero alla variazione di volume $\Delta V.$

$L = p\Delta V$

Anche nel caso in cui il gas venga compresso, facendo i conti viene lo stesso risultato.

Grazie a questo possiamo calcolare il lavoro e il calore fatto da una trasformazione isocora o una isobara:

Se si tratta di una trasformazione isocora, il volume è costante, perciò $\Delta V$ è $0$ e anche il lavoro sarà nullo. Infatti se non cambia volume non può spingere nessun pistone.

Siccome $Q - L = \Delta U,$ avremo $Q = \Delta U.$

Nella trasformazione isobara, invece, avremo $L = p\Delta V$ e quindi anche $Q = \Delta U + p\Delta V.$

Nella trasformazione adiabatica, invece, per definizione avremo $Q = 0$ e quindi $L = - \Delta U.$

Nell' isoterma, invece, avremo $\Delta U = c_v n \Delta T$ $= c_v n \cdot 0 = 0,$ perciò $L = Q.$ Utilizzando gli integrali si può dimostrare che $L = nRT \ln{V_f \over V_i},$ dove $V_f$ è il volume finale a $V_i$ è il volume iniziale.

La dimostrazione tramite integrali di questa formula si trova sotto questa tabella riassuntiva che riporta i vari lavori e calori delle trasformazioni termodinamiche:

Ecco la dimostrazione del lavoro di una trasformazione isoterma:

Per definizione avremo:

$L_{A \to B} = \int_A^B \overrightarrow{F}\cdot \overrightarrow{ds}$

Dove $A$ e $B$ sono gli stati iniziali e finali del gas.

Come prima si può dimostrare che $\overrightarrow{F}\cdot d\overrightarrow{s} = p \cdot dV$ e quindi possiamo sostituire ottenendo:

$L_{A \to B} = \int_A^B p \cdot dV$

Ma l'equazione di stato dei gas ci dice che $pV = nRT$ e quindi $p = {nRT \over V}.$ Quindi:

$L_{A\to B} = \int_A^B {nRT \over V} dV$

$L_{A\to B} = nRT \ln{V} |_A^B$

$L_{A\to B} = nRT \ln(V_B) - nRT\ln(V_A)$

Utilizzando le proprietà dei logaritmi:

$L_{A\to B} = nRT\ln({V_B \over V_A})$

$V_B$ e $V_A$ sarebbero infatti i volumi finali ed iniziali e dunque questa formula qua è uguale a quella di prima.