Teorema di pitagora

Prendiamo un triangolo rettangolo:

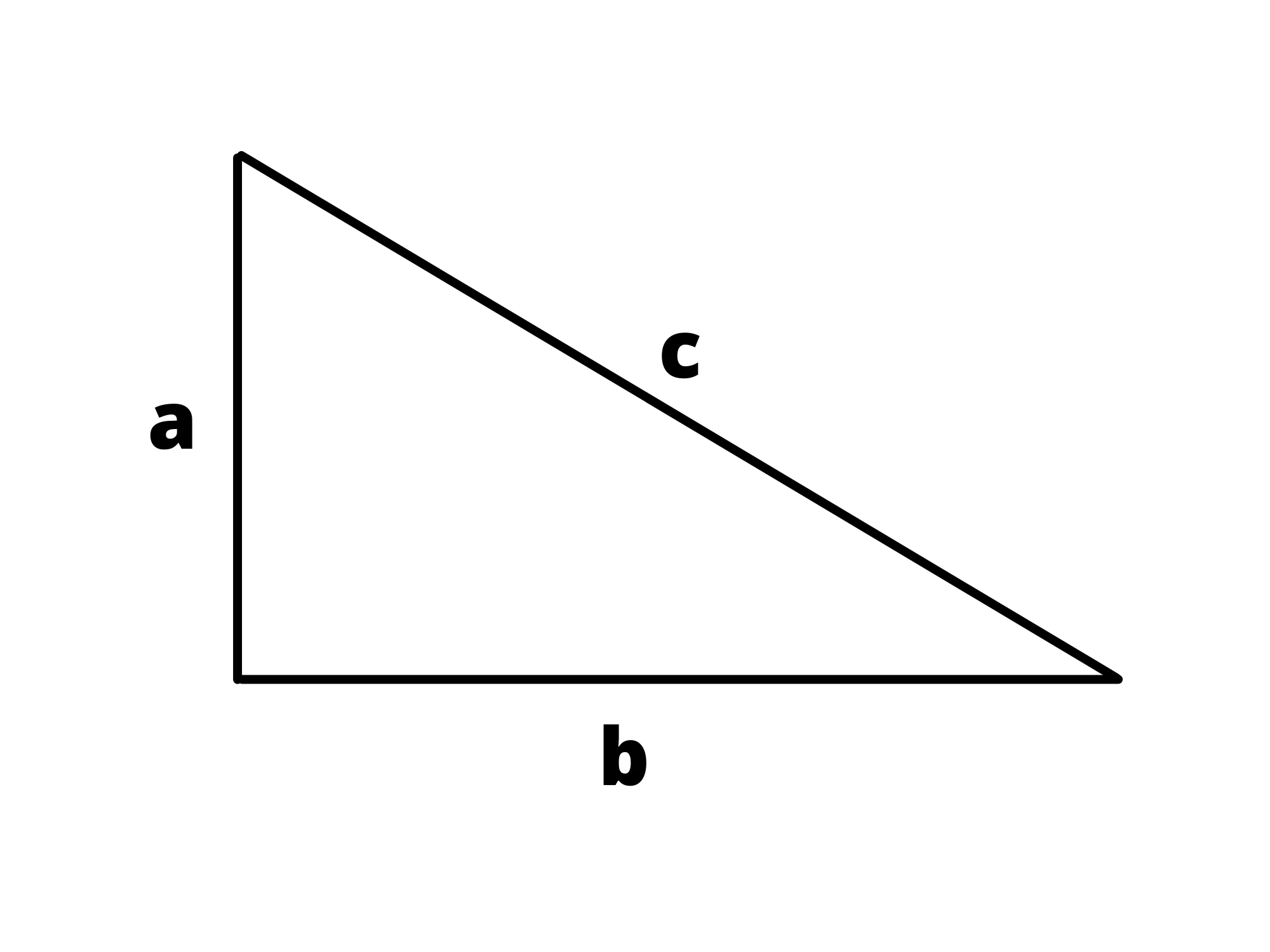
I due lati adiacenti all'angolo retto ($a$ e $b$) sono detti cateti, mentre il terzo lato, quello "lontano" dall'angolo retto è detto ipotenusa.

Il teorema di Pitagora lega tra loro la lunghezza dei cateti e quella dell'ipotenusa. Esso infatti afferma che:

La somma dei quadrati costruiti sui cateti (di un triangolo rettangolo) è uguale al quadrato costruito sull'ipotenusa.

Algebricamente lo si può tradurre come:

Quindi, a cosa ci serve questo teorema? Con esso possiamo trovare l'ipotenusa conoscendo i cateti, oppure possiamo trovare un cateto conoscendo l'altro e l'ipotenusa, basta isolare l'incognita desiderata nell'equazione:

$c=\sqrt{a^2 + b^2 }$ per trovare l'ipotenusa

$a=\sqrt{c^2 -b^2}$ per trovare il cateto $a$

$b=\sqrt{c^2 -a^2 }$ per trovare il cateto $b$

Vediamo un esempio di come possiamo applicarlo:

un triangolo rettangolo ha cateti $a$ e $b$ sono lunghi rispettivamente $3cm$ e $4cm$ , trovare la lunghezza dell'ipotenusa

Per farlo basta utilizzare il Teorema di Pitagora, che ci dice:

$c^2 = a^2 + b^2$

ovvero:

$c=\sqrt{a^2 +b^2}$

Quindi basta sostituire $a$ e $b$ per trovare l'ipotenusa $c$ :

$c=\sqrt{(3cm)^2 + (4cm)^2 }$ $= \sqrt{9cm^2 + 16cm^2}=$ $\sqrt{25cm^2}=5cm$

Ed ecco risolto. In questo caso abbiamo ottenuto tre valori interi per i lati del triangolo $(3,4,5)$ e siccome dobbiamo prendere un radice quadrata è piuttosto raro che escano dei numeri interi.

Questa terna di numeri viene chiamata terna pitagorica e quella che abbiamo appena visto $3,4,5$ è la più piccola che esista. Perché ci interessano le terne pitagoriche? Perché in alcuni casi ci aiutano a semplificare i calcoli.

Notiamo infatti una cosa interessante: se moltiplichiamo ogni termine della terna pitagorica per un numero intero $k$ , otteniamo un'altra terna pitagorica. Perchè?

Dimostriamolo:

una volta moltiplicati per $k$ , la nuova terna diventerà $(3k,4k,5k)$ , applichiamo il teorema di Pitagora e vediamo se lo verificano:

$c^2 = a^2 + b^2$

$25k^2 = 9k^2 + 16k^2$

$25k^2 = 25k^2$

L'uguaglianza è verificata. Geometricamente questo ha senso perché moltiplicare ogni lato per una costante $k$ equivale a rimpicciolire o ingrandire il triangolo, quindi è ovvio che rimarrà un triangolo rettangolo.

Ma perché abbiamo fatto tutto questo? Perché ora se abbiamo, ad esempio, due cateti di lunghezza $6cm$ e $8cm$, sappiamo subito che l'ipotenusa sarà lunga $10cm$ .

I cateti sono infatti quelli della terna pitagorica ma moltiplicati per $2$ , quindi $k=2$ e dunque l'ipotenusa deve essere il doppio di $5cm$ , ovvero $10cm$ .

Se quindi vi capita di trovare due cateti nella forma $3k$ e $4k$ , sapete già che l'ipotenusa sarà $5k$ . Questo è specialmente utile per $k$ molto grandi.

Se per esempio avessimo due cateti lunghi $39cm$ e $52cm$ , sarebbe un po' lungo fare i calcoli perché li dovreste elevare al quadrato, sommarli e prendere la radice quadrata. Se però notate che:

$39=13 \cdot 3$ e $52= 13 \cdot 4$, sapete già che l'ipotenusa sarà $13 \cdot 5$, ovvero $60$. Esistono poi altre terne pitagoriche utili da sapere a memoria, ma per ora ci fermiamo qui.

Primo teorema di Euclide

Passiamo quindi ai Teoremi di Euclide. Sono molto meno famosi e generalmente meno utili del Teorema di Pitagora, ma ci possono aiutare a risolvere molti problemi.

Il primo teorema di Euclide enuncia che:

Il quadrato costruito su uno dei cateti (in un triangolo rettangolo) è equivalente al rettangolo che ha per dimensioni la proiezione del cateto sull'ipotenusa e l'ipotenusa stessa.

Cosa si intende per proiezione del cateto sull'ipotenusa? Si intende che dal vertice che il cateto non ha in comune con l'ipotenusa, in questo caso $A$ , facciamo partire una retta perpendicolare all'ipotenusa, che la intersecherà in un punto $H$ .

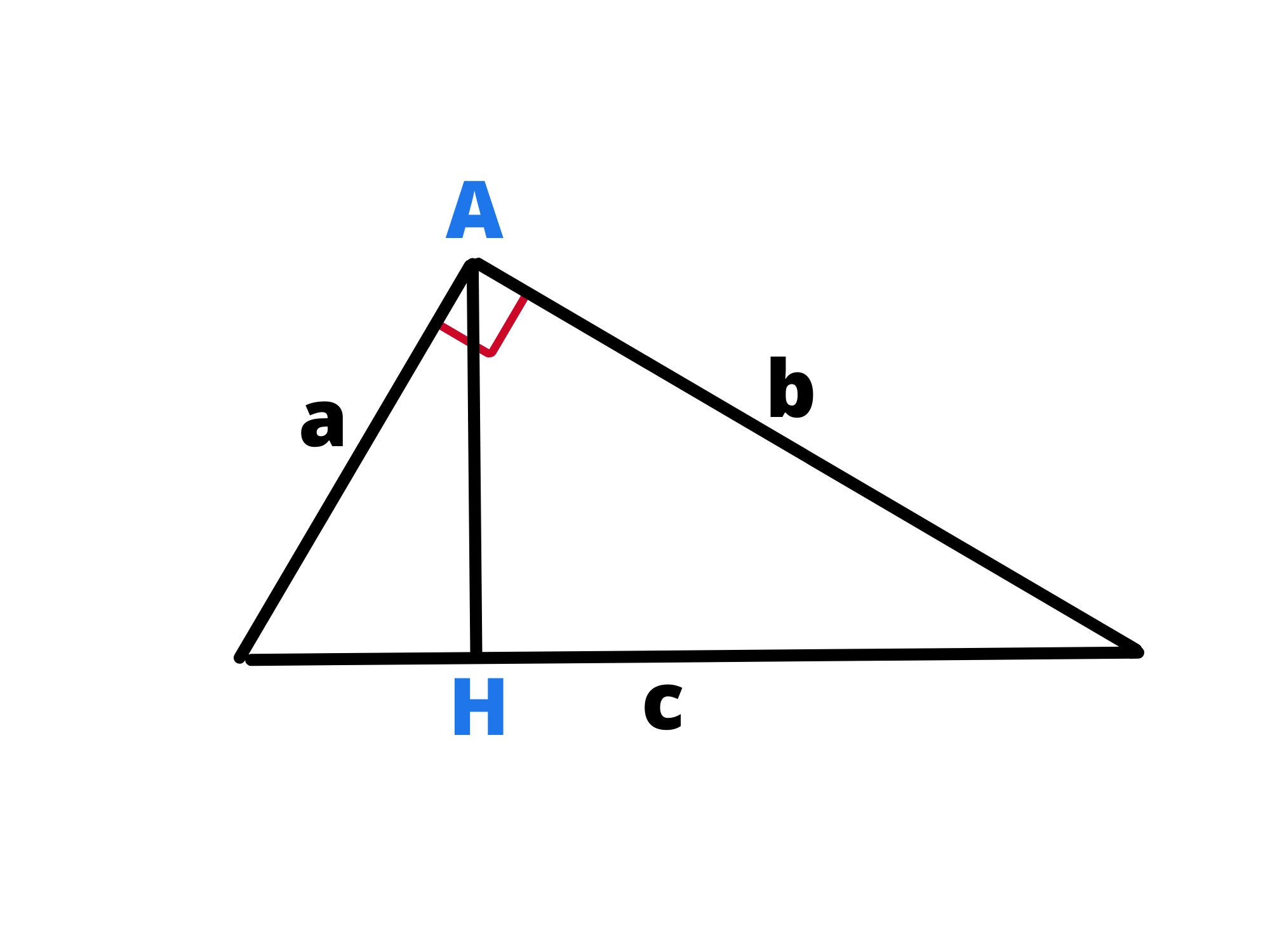
Finora abbiamo effettuato un procedimento analogo a quello per trovare l'altezza di un triangolo, adesso però la proiezione è il segmento $BH$ , ovvero quello che parte del vertice in comune $(B)$ e l'intersezione $H$ .

Potete visualizzare il processo di prendere la proiezione come al guardare l'ombra del cateto se la luce viene dall'alto.

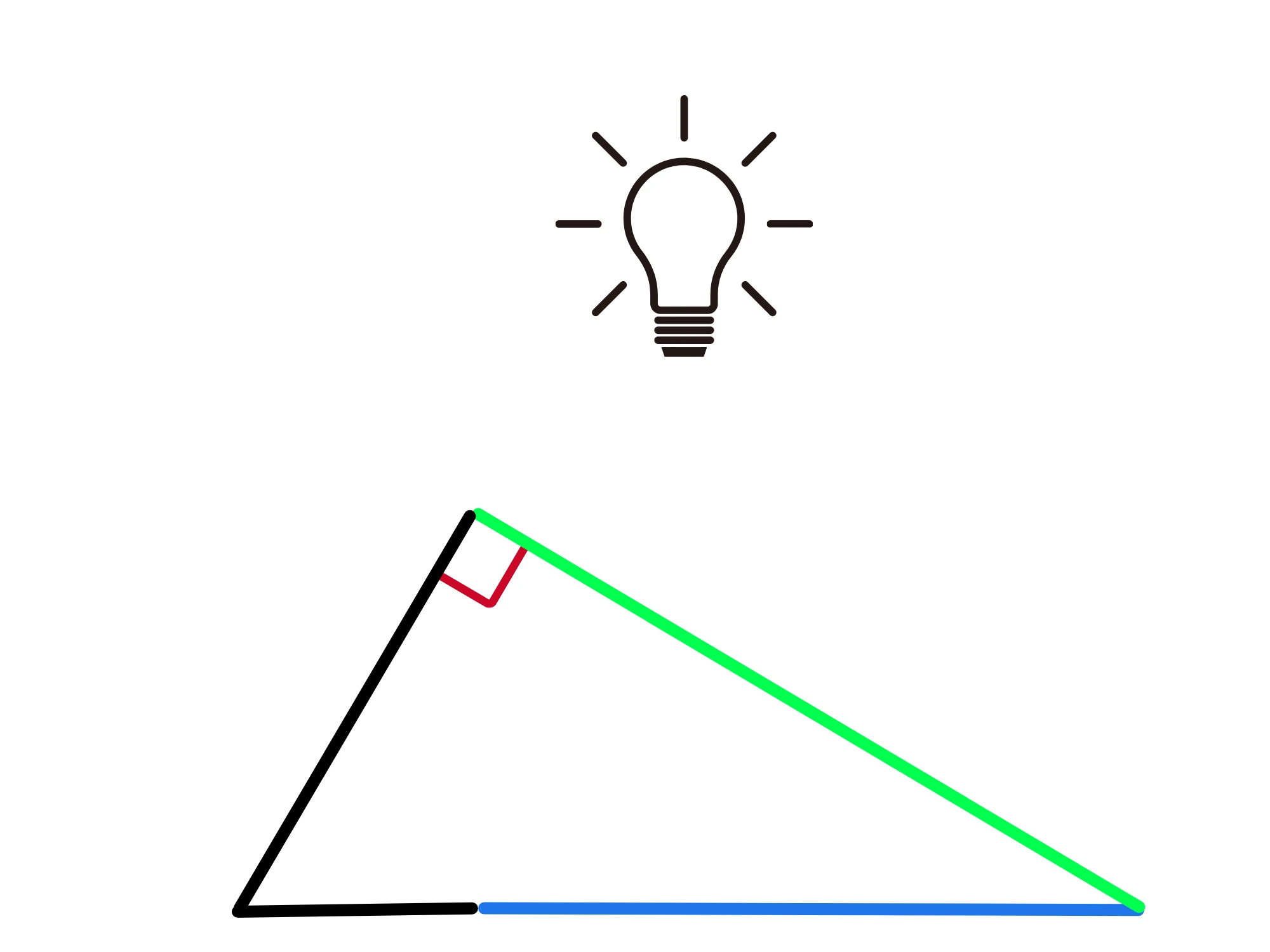
Proviamo a tradurre in forma algebrica quello che enuncia il teorema. Se chiamiamo la proiezione $p$ , avremo:

$a^2 = p \cdot c$

Utilizzando la proprietà fondamentale delle proporzioni possiamo riscriverla come:

Ovvero, il rapporto tra l'ipotenusa ed un cateto è uguale al rapporto tra quel cateto e la sua proiezione sull'ipotenusa.

Secondo teorema di Euclide

Il secondo teorema di Euclide enuncia che:

Il quadrato costruito sull'altezza (in un triangolo rettangolo) riferita all'ipotenusa è uguale al rettangolo che ha come dimensioni le due proiezioni dei cateti sull'ipotenusa.

Guardando al disegno del capitolo precedente, se chiamiamo le due proiezioni $p_1$ e $p_2$ e l'altezza la chiamiamo $h$ , avremo:

$h^2 = p_1 \cdot p_2$

Anche in questo caso possiamo riscriverla come proporzione grazie alla proprietà fondamentale delle proporzioni: