Superficie e volume dei solidi

In questa lezione vedremo come calcolare il volume e la superficie di varie tipologie di solidi.

Cosa sono il volume e la superficie?

Il volume equivale allo spazio occupato dal solido, mentre la superficie è la somma delle aree delle varie figure che lo delimitano.

Indicheremo la superficie di tutte le basi del solido come $\displaystyle { S_b }$ , mentre chiameremo la superficie laterale $\displaystyle { S_l }$ . La superficie totale sarà indicata come $\displaystyle { S_t }$ o come $\displaystyle { S }$ se è sottinteso che si tratti di essa.

Di seguito precederemo analizzando un solido alla volta:

Cubo

Il cubo è un poliedro formato da sei facce quadrate uguali tra loro:

Se chiamiamo il suo lato $\displaystyle { l }$ , l'area di ogni sua faccia sarà uguale a $\displaystyle { l^2 }$ , dunque la superficie totale sarà:

S=6l^2

Sappiamo bene, poi, che il volume del cubo vale $\displaystyle { l^3 }$ :

V=l^3

Parallelepipedo

Il parallelepipedo è un poliedro formato da sei parallelogrammi (solitamente sono sei rettangoli) a due a due congruenti e paralleli:

Esso avrà dimensioni $\displaystyle { a,b }$ e $\displaystyle { c }$ . La sua superficie sarà formata da due basi di area $\displaystyle { ab }$ e da altri $\displaystyle { 4 }$ rettangoli, due con area pari a $\displaystyle { bc }$ e due con area $\displaystyle { ac }$ .

Dunque la sua superficie di base sarà:

$\displaystyle { S_b = 2ab }$

e quella laterale sarà:

$\displaystyle { S_l=2bc + 2ac }$

Quindi la superficie totale è uguale a:

$\displaystyle { S_t= S_b + S_l = 2ab + 2bc +2ac }$

Cioè:

S_t = 2 (ab + bc + ac)

Il suo volume è invece pari al prodotto delle dimensioni:

V=abc

Prisma retto

Il prisma retto è un poligono con due due basi una sopra all'altra collegate tra loro tramite rettangoli:

Vengono detti "retti" perché i rettangoli sono perpendicolari alle basi.

La base può essere qualsiasi poligono, dunque l'area della base varia da prisma in prisma. Chiamiamola dunque come una generica $\displaystyle { A_b }$ . Avendo in totale due basi, la superficie di base sarà uguale a:

$\displaystyle { S_b = 2A_b }$

Per calcolare la superficie laterale, invece, possiamo notare che è formata dalla somma delle aree dei rettangoli. Ognuno di loro ha area uguale a $\displaystyle { hl_n }$ , dove $\displaystyle { h }$ è l'altezza del prisma e $\displaystyle { l_n }$ è la lunghezza dell'ennesimo lato della base:

Prisma retto — Superficie laterale di un prisma S_b = 2A_b Per calcolare la superficie laterale, invece, possiamo notare che

Dunque avremo:

$S_l = hl_1 + hl_2 + h_3 +...$

Raccogliendo $h$ otteniamo:

$S_l = h(l_1 + l_2 + l_3 +...)$

Notiamo che la somma dei lati della base è, per definizione, il perimetro della base, che possiamo chiamare $2P_b.

Dunque, la superficie laterale del prisma retto è uguale alla sua altezza per il perimetro della base:

S_l = h\cdot 2P_b

Il volume del prisma, invece, è uguale all'area della base per l'altezza:

V= A_bh

Piramide retta

Andiamo avanti con la piramide retta :

E' detta piramide retta perché il segmento che congiunge il vertice con il centro della base deve formare un'angolo retto con quest'ultima:

Piramide retta — Piramide retta Andiamo avanti con la piramide retta: E' detta piramide retta perché il segmento che…

La sua superficie di base dipende dalla forma della base: può essere un triangolo, un quadrato, un esagono e così via. Chiamiamola, dunque, come una generica $S_b.$

La superficie laterale, invece, equivale alla somma delle aree dei triangoli. Se la base della piramide è un poligono regolare, allora questi triangoli saranno tutti uguali.

Adesso tracciamo l'altezza $\displaystyle { a }$ rispetto al lato della base $\displaystyle { l }$ :

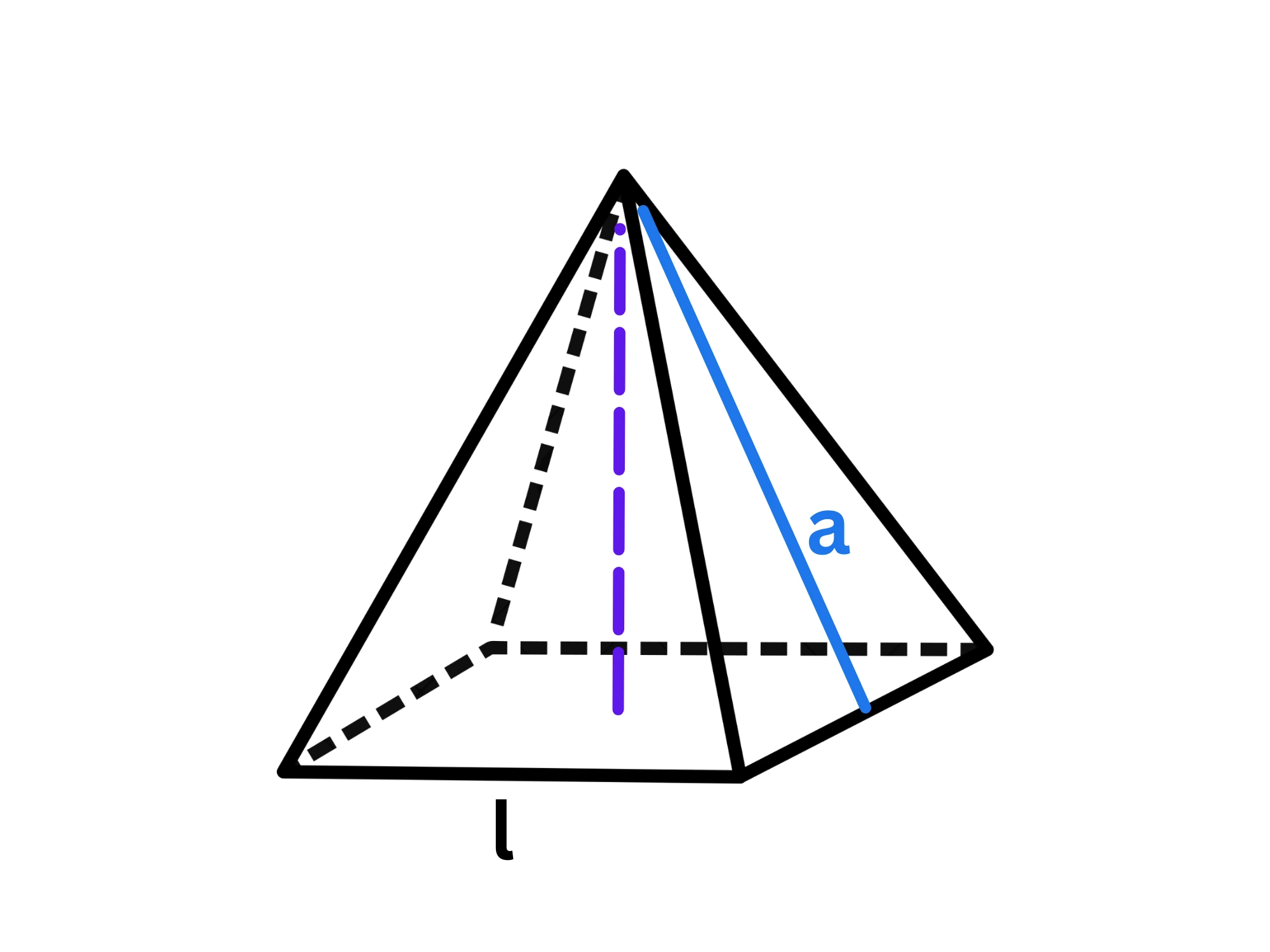
Piramide retta — Piramide retta, apotema indicata con "a" e lato di base "l".

Questa altezza viene chiamata apotema e per questo viene indicata con la lettera $\displaystyle { a }$ .

Siccome l'area di un triangolo è uguale alla base per l'altezza, allora l'area di ogni triangolino sarà uguale a ${al\over 2}.$

Se il poligono ha $n$ lati, allora sommando tutte ed $n$ le basi otteniamo:

$\displaystyle { S_l = {anl\over 2} }$

Notiamo però che $\displaystyle { nl }$ equivale al perimetro $\displaystyle { 2P_b }$ della base. Dunque:

S_l = {a \cdot 2P_b\over 2}

Infine, se chiamiamo l'altezza della piramide $\displaystyle { h }$ , il suo volume sarà uguale a:

V= {A_bh\over 3}

Cilindro

Passiamo ora a qualche solido più curvo. La superficie di base del cilindro è formata da cerchi di raggio $\displaystyle { r }$ , dunque avremo:

$ $\displaystyle { S_b= 2\pi r^2 }$ $$

Per la superficie laterale, invece, se la srotoliamo:

$Cilindro — Superficie del cilindro $ S_b= 2\pi r^2 $$ Per la superficie laterale, invece, se la srotoliamo: Otteniamo un$

Otteniamo un rettangolo con altezza pari all'altezza del cilindro e con base uguale alla circonferenza del cerchio. Avremo quindi:

S_l = 2\pi r h

Infine, il volume è uguale all'area della base $\displaystyle { A_b }$ per l'altezza, ovvero:

V= h A_b = h\pi r^2

Cono

Prendiamo un cono:

$Cono — Cono Cono Prendiamo un cono: La sua superficie di base sarà uguale all'area del cerchio, ovvero a: $$ S_b= \p$

La sua superficie di base sarà uguale all'area del cerchio, ovvero a:

S_b= \pi r^2

Se andiamo ad "effettuare un taglio" sull'apotema e lo srotoliamo:

$Cono — Superficie del cono $$ S_b= \pi r^2 $$ Se andiamo ad "effettuare un taglio" sull' apotema e lo srotoliamo: ott$

otteniamo un triangolo con altezza pari all'apotema e con base pari alla circonferenza.

Di conseguenza, la superficie laterale sarà uguale a:

S_l = \pi r a

Il volume, invece, equivale alla superficie di base moltiplicata per l'altezza diviso $\displaystyle { 3 }$ :

V= {h \pi r^2 \over 3}

Se avete fatto attenzione, avrete probabilmente notato molte analogie tra il parallelepipedo e il cilindro e tra la piramide e il cono. Queste analogie possono aiutarvi a ricordare le formule.

Sfera

Vediamo quindi l'ultimo solido rimasto di questa lezione: la sfera.

La sua superficie è uguale a:

S= 4\pi r^2

Mentre il suo volume è pari a:

V= {4\over 3} \pi r^3

#Geometria euclidea 🎓 1º Scientifico 🎓 2º Scientifico 🎓 1º Classico 🎓 2º Classico 🎓 1º Linguistico 🎓 2º Linguistico 🎓 3º Media

Hai trovato utile questa lezione?