Andiamo avanti con la piramide retta :

E' detta piramide retta perché il segmento che congiunge il vertice con il centro della base deve formare un'angolo retto con quest'ultima:

La sua superficie di base dipende dalla forma della base: può essere un triangolo, un quadrato, un esagono e così via. Chiamiamola, dunque, come una generica
La superficie laterale, invece, equivale alla somma delle aree dei triangoli. Se la base della piramide è un poligono regolare, allora questi triangoli saranno tutti uguali.
Adesso tracciamo l'altezza rispetto al lato della base :
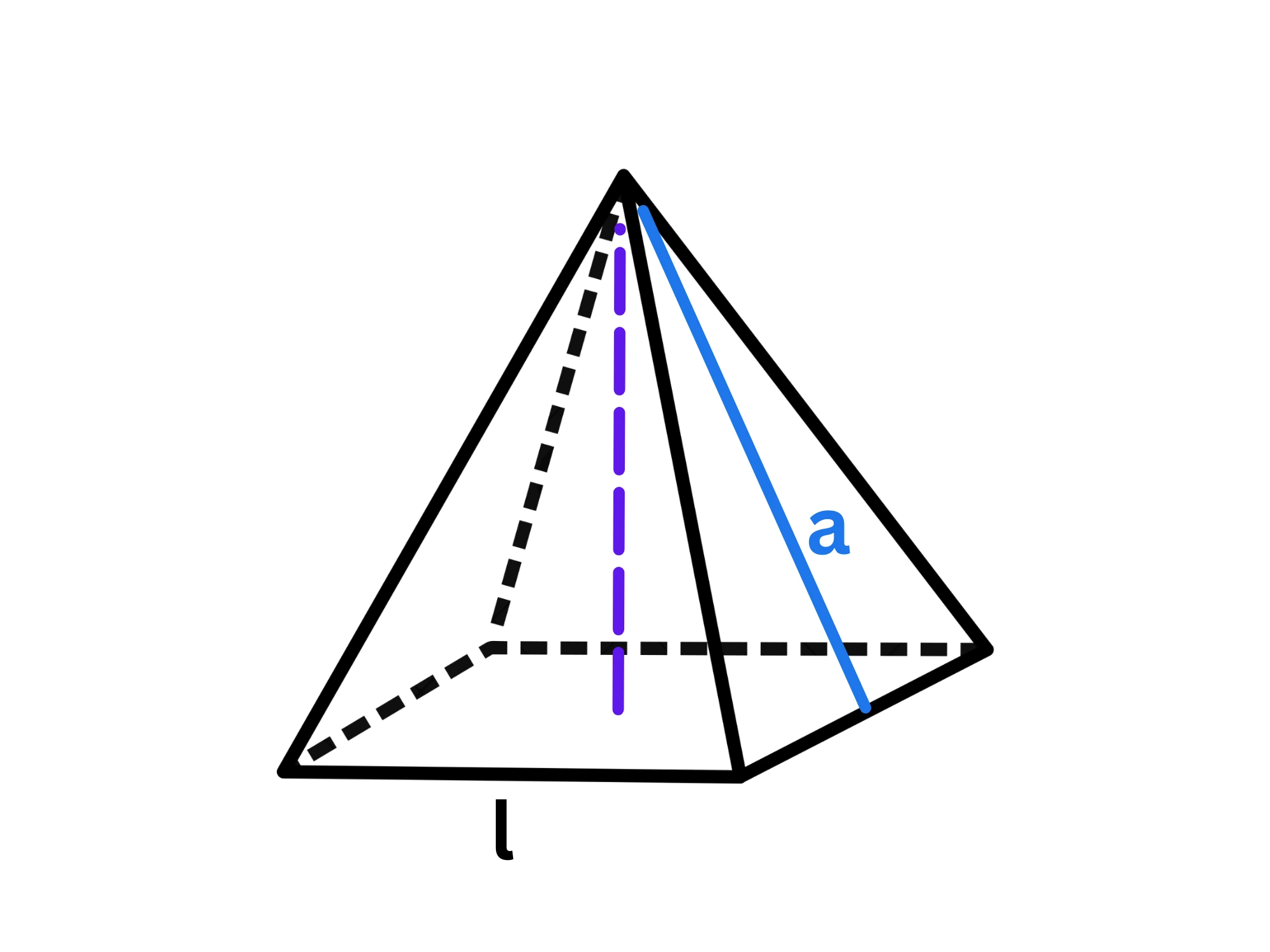
Questa altezza viene chiamata apotema e per questo viene indicata con la lettera .
Siccome l'area di un triangolo è uguale alla base per l'altezza, allora l'area di ogni triangolino sarà uguale a
Se il poligono ha lati, allora sommando tutte ed le basi ottenniamo:
Notiamo però che equivale al perimetro della base. Dunque:
Infine, se chiamiamo l'altezza della piramide , il suo volume sarà uguale a: