Prima di iniziare con lo studio delle rette analizziamo il piano cartesiano. Per introdurlo dovete avere chiari i concetti di piano e di retta.
Il piano cartesiano è uno strumento che ci permette di descrivere la posizione di oggetti nel piano.
Esso è costituito da due rette, chiamate assi, che si incontrano in un punto chiamato origine.
La retta orizzontale si chiama asse delle (o asse delle ascisse) e quella verticale si chiama asse delle (o asse delle ordinate).
Gli assi sono orientati e su essi è fissata un’unità di misura. L’origine corrisponde a e su essi è possibile inserire ogni numero reale.
Prendiamo un punto nel piano e tracciamo le rette parallele agli assi. Chiamiamo con il punto di intersezione di una retta con l’asse delle ascisse e con il punto di intersezione dell’altra retta con l’asse delle ordinate.
Chiamiamo quindi ascissa e ordinata di e diciamo che ha coordinate e .
Possiamo anche utilizzare la notazione che si legge A ha coordinate e . Notiamo che l’ascissa va scritta sempre prima dell’ordinata.
Gli assi dividono il piano in parti (anch'esse infinite) chiamate quadranti come in figura. Notiamo che se un punto del piano si trova
Analizziamo come si trova la distanza fra due punti nel piano cartesiano. Partiamo da un caso particolare in cui le ascisse dei due punti sono uguali. Prendiamo quindi due punti con ascissa uguale e .
Siccome si trovano sulla stessa retta orizzontale, la distanza fra i due punti sarà la differenza tra le loro ordinate.
Attenzione però, la distanza è una quantità sempre positiva! Per questo bisogna prendere il valore assoluto. Quindi la formula è
Per lo stesso identico ragionamento, se abbiamo due punti con la stessa ordinata e , la loro distanza sarà il valore assoluto della differenza delle loro ascisse:
Analizziamo ora il caso generale di due generici punti e .
Per prima cosa, tracciamo le parallele all’asse e all’asse che partono dai due punti. Notiamo che si forma un triangolo rettangolo. Uno dei suoi cateti è uguale alla differenza delle mentre l’altro alla differenza delle .
Quindi possiamo usare il teorema di Pitagora per trovare la distanza tra i due punti:
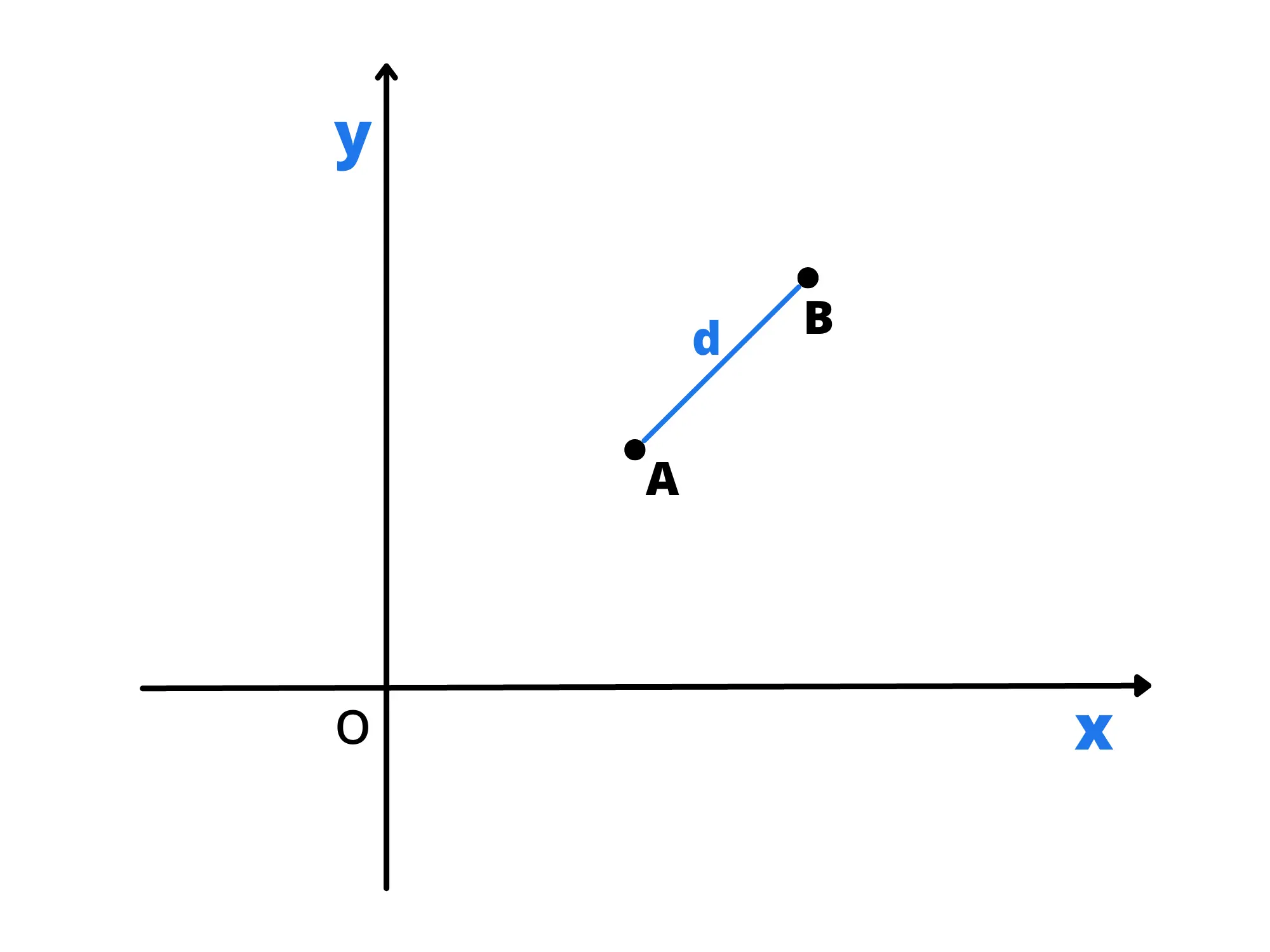
Notiamo che questa volta non ci dobbiamo preoccupare del segno della differenza perché elevando al quadrato le differenze diventa comunque tutto positivo.
Un'ultima formula che è utile conoscere è quella che determina le coordinate del punto medio di un segmento nel piano cartesiano. Essa è
dove e sono le coordinate dei due estremi del segmento.