Cosa sono gli insiemi numerici?

Gli insiemi numerici sono insiemi infiniti che raggruppano una determinata categoria di numeri. Partiamo subito con il primo!

Insieme dei numeri naturali $\mathbb{N}$

Il simbolo è semplice da ricordare: $\mathbb{N}$ di “naturali” . Il tratto obliquo si scrive due volte per differenziarlo da una generica $N$ maiuscola.

Allora cosa sono i numeri naturali? Concettualmente si possono immaginare come tutti i numeri interi positivi. Si definiscono però come tutti i numeri che puoi ottenere partendo da $0$ ed aggiungendo una unità alla volta (ovvero sommando $1$ ). Quindi avremo:

$\mathbb{N} = {0,1,2,3,4,5,6,7,…}$

Sono diffusi online video matematici che litigano per decidere se $0$ appartiene ai numeri naturali o no. Infatti ci sono ancora dei dibattiti su questo argomento, ma in generale $0$ viene accettato come appartenente ai numeri naturali.

Siccome li usiamo per contare, gli elementi di $\mathbb{N}$ oltre ad essere chiamati numeri naturali, vengono talvolta chiamati numeri cardinali.

Insieme dei numeri relativi $\mathbb{Z}$

I numeri relativi sono tutti gli interi caratterizzati da un segno, che può essere positivo ( $+$ ), nullo (lo $0$ ), o negativo ( $-$ ). Quindi ad $\mathbb{N}$ aggiungiamo tutti gli interi negativi.

$\mathbb{Z} ={…,-3,-2,-1,0,+1,+2,+3,…}$

Il simbolo da ricordare questa volta è meno intuitivo, ma anche in questo caso, per differenziare $\mathbb{Z}$ da una generica $Z$, scriviamo due volte il lato obliquo.

Notate che se chiamiamo tutti i numeri negativi $\mathbb{N^-}$

$\mathbb{Z} ={0, -1, -2, -3, -4,…}$

Avremo che $\mathbb{Z}$ sarà l’unione di $\mathbb{N}$ e $\mathbb{N^-}$ :

$\mathbb{Z} =\mathbb{N} \cup \mathbb{N^-}$

Di conseguenza $\mathbb{N}$ è un sottoinsieme di $\mathbb{Z}$ .

Insieme dei numeri razionali $\mathbb{Q}$

I numeri razionali sono i tutti i numeri esprimibili come rapporto tra due numeri relativi. In altre parole, sono tutte le frazioni formate da numeri interi. Quindi, come per i numeri relativi, i numeri razionali sono caratterizzati da un segno: positivo (+), nullo (lo 0), o negativo (-).

Dobbiamo però aggiungere una restrizione. Il numero relativo che sta al denominatore non può essere uguale a $0$ , perché non si può dividere per 0.

Quindi:

$c \in \mathbb{Q} \leftrightarrow c={ a \over b},$ con $a,b \in \mathbb{Z},b \neq 0$

Se si pensa che in inglese “rapporto” si dice “quotient”, il perché della $\mathbb{Q}$ come simbolo ha più senso. Come per gli altri, mettiamo due volte il cerchietto per differenziare $\mathbb{Q}$ dalla generica $Q$ .

Esempi di numeri razionali sono:

• ${1 \over 2},{10 \over 7},-8,-{2 \over 3},-{9 \over 17},5,{4 \over 3}$

$-8$ e $5$ sono numeri razionali? Certo, hanno soltanto $1$ al denominatore. Infatti $-8={-8 \over 1}.$

Di conseguenza i numeri razionali contengono tutti i numeri relativi, ovvero $\mathbb{Z}$ è un sottoinsieme di $\mathbb{Q}.$

Insieme dei numeri irrazionali $\mathbb{I}$

Ai tempi di Pitagora si pensava che tutti i numeri fossero esprimibili tramite frazioni di numeri interi (i nostri numeri razionali). Però, osservarono che la diagonale di un quadrato di lato $1$ , per il teorema di Pitagora, doveva essere uguale a $\sqrt2 .$ Dimostrarono che questo numero non era esprimibile tramite rapporto di numeri interi. Scoprirono così i numeri irrazionali.

Come avrete intuito, i numeri irrazionali sono tutti i numeri che non sono esprimibili tramite una frazione formata da numeri interi.

Tra questi ci sono tutte le radici quadrate di numeri che non sono quadrati perfetti, ma anche $\pi$ e molte altre costanti che si trovano in giro.

Questa volta la $\mathbb{I}$ è facile da ricordare perché sta per “irrazionale” . Come per gli altri mettiamo un doppio tratto per differenziarla dalla generica $I.$

Quindi esempi di numeri irrazionali sono:

• $\sqrt2 ,\sqrt5 , \pi,\sqrt{7 \over 3},{1 \over \sqrt{10}}$

Insieme dei numeri reali $\mathbb{R}$

Adesso che conosciamo i numeri razionali e i numeri irrazionali, sarebbe molto pratico avere un insieme che li contiene entrambi, l’insieme dei numeri reali:

$\mathbb{R} = \mathbb{Q} \cup \mathbb{I}$

La $\mathbb{R}$ che sta per “reali” anche questa volta ha un doppio tratto per differenziarla dalla generica $R$.

Quindi esempi di numeri reali sono:

• $2,{7 \over 4},\sqrt7$

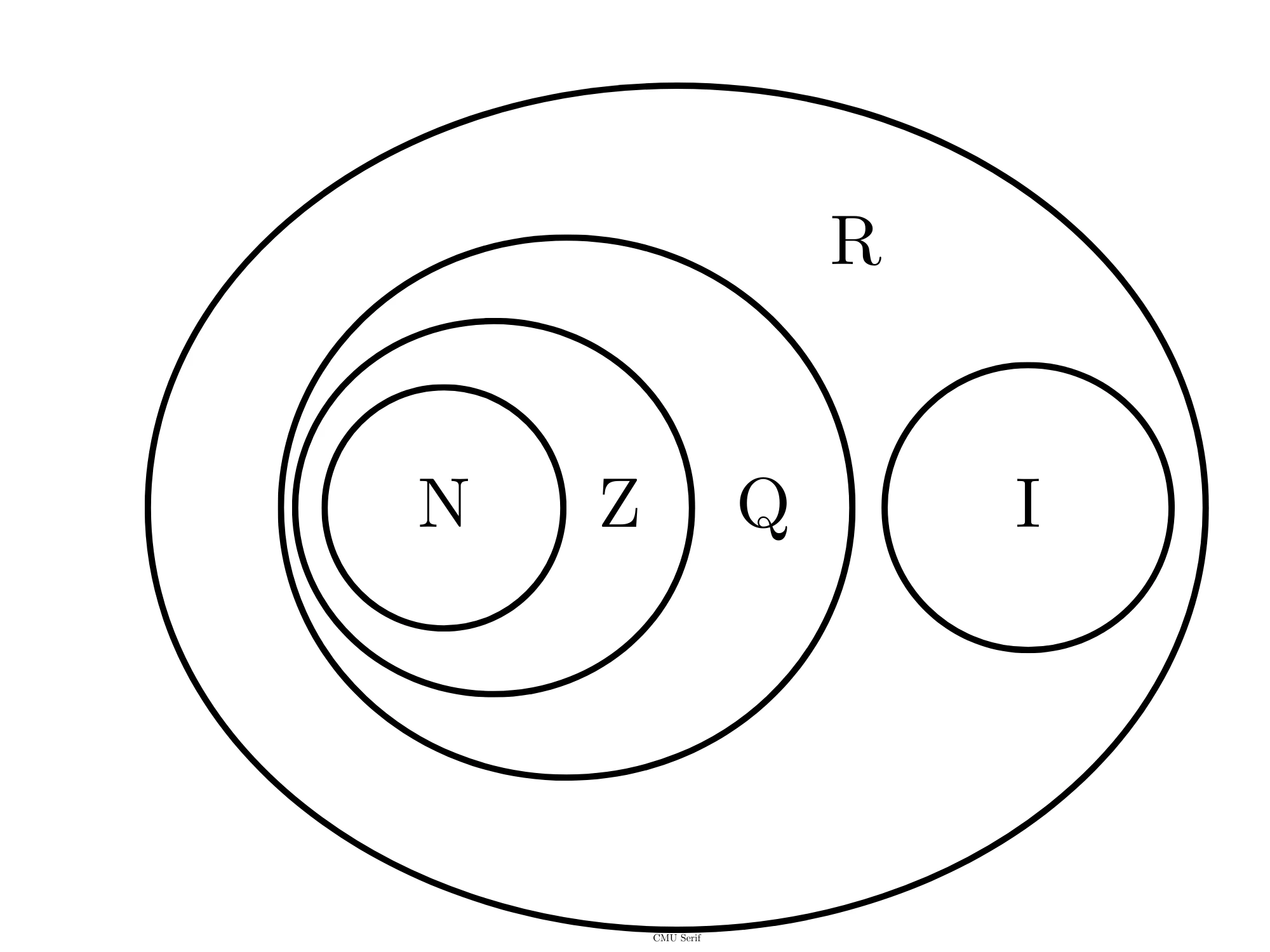
Per comprendere poi meglio i legami tra i vari insiemi numerici proponiamo il seguente grafico di Eulero-Venn: