Energia potenziale elettrica

La forza elettrostatica è conservativa

Prima di tutto dobbiamo capire che la forza elettrostatica è una forza conservativa.

Che cosa significa? Significa che se partiamo da un punto $\displaystyle { A }$ e ci spostiamo ad un punto $\displaystyle { B, }$ il lavoro fatto dalla forza elettrostatica non dipende dal percorso fatto, ma solo da $\displaystyle { A }$ e $\displaystyle { B }$ (e dalla forza elettrostatica).

Quindi per tutti i percorsi che vediamo qui sotto, il lavoro fatto dalla forza elettrostatica è sempre uguale:

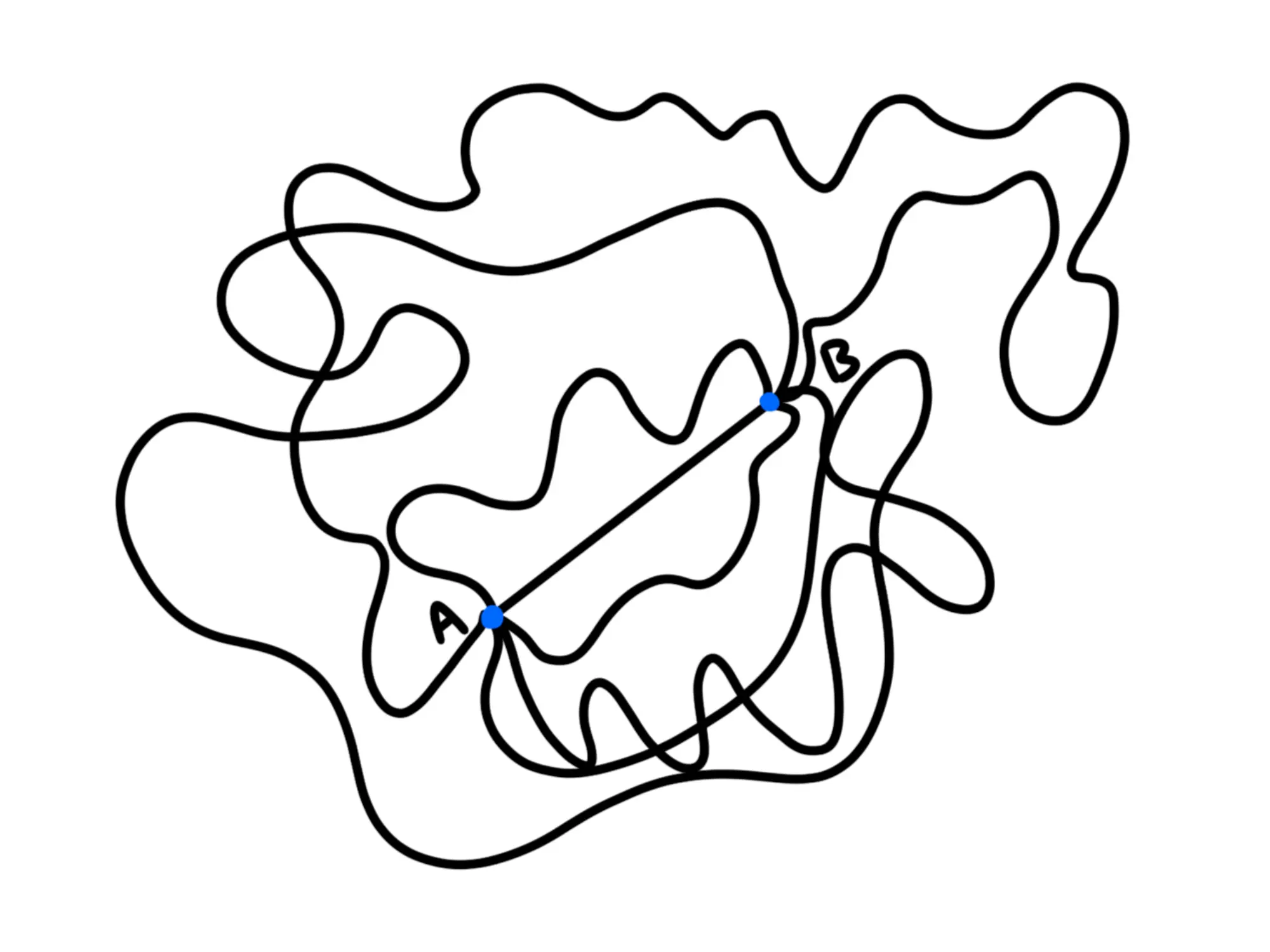
Questo è molto importante e se vi ricordate, quando avevate studiato l'energia e il lavoro, avevate imparato che il lavoro fatto dalle forze conservative è uguale a meno la differenza di energia potenziale, cioè:

Ma cos'è quest'energia potenziale? Vediamolo meglio con l'esempio di una particella vicina ad un piano infinito uniformemente carico:

Energia potenziale elettrica

Iniziamo quindi con un esempio:

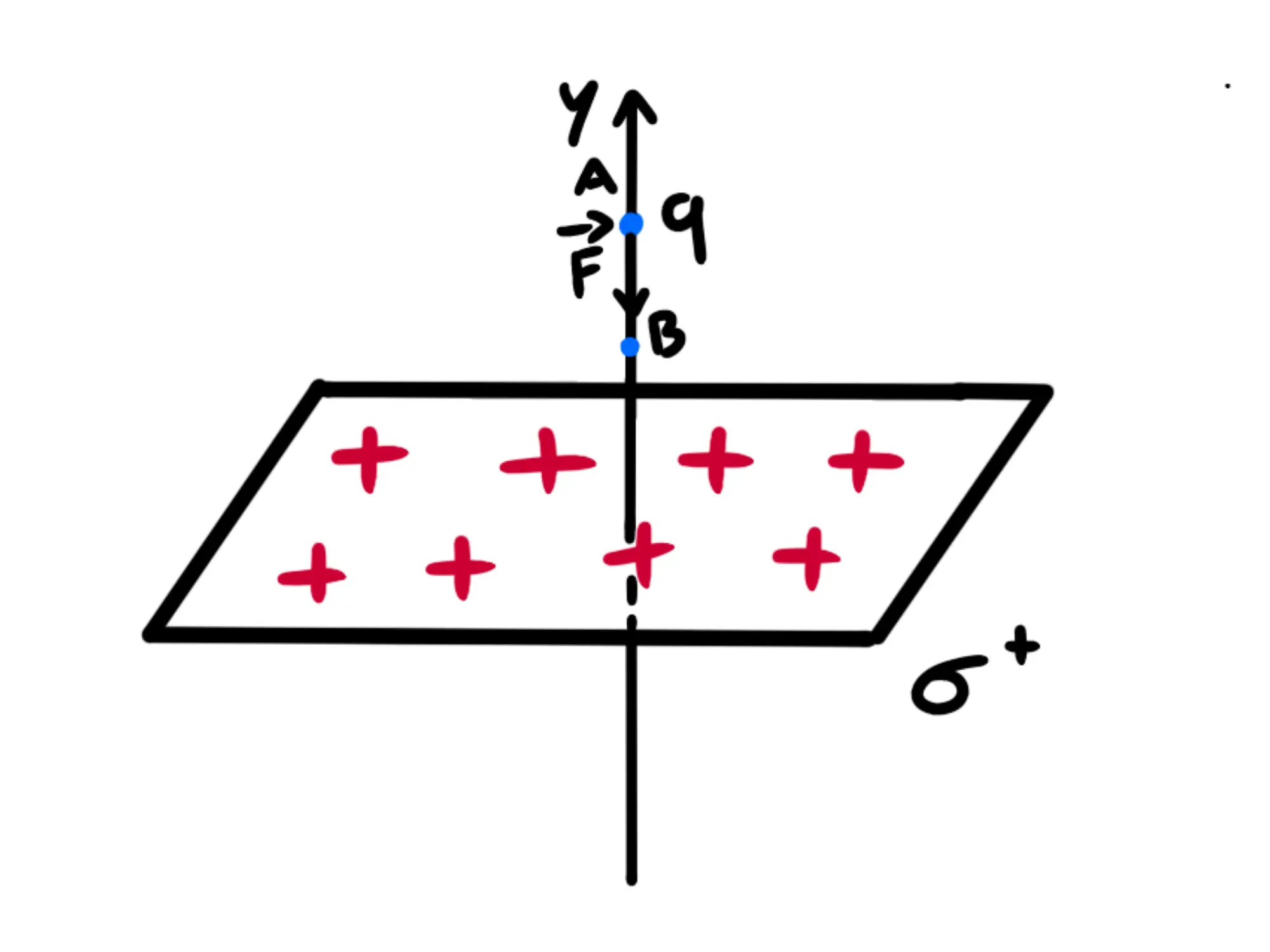
Abbiamo un piano infinito carico positivamente e uniformemente e una carica negativa $\displaystyle { q: }$

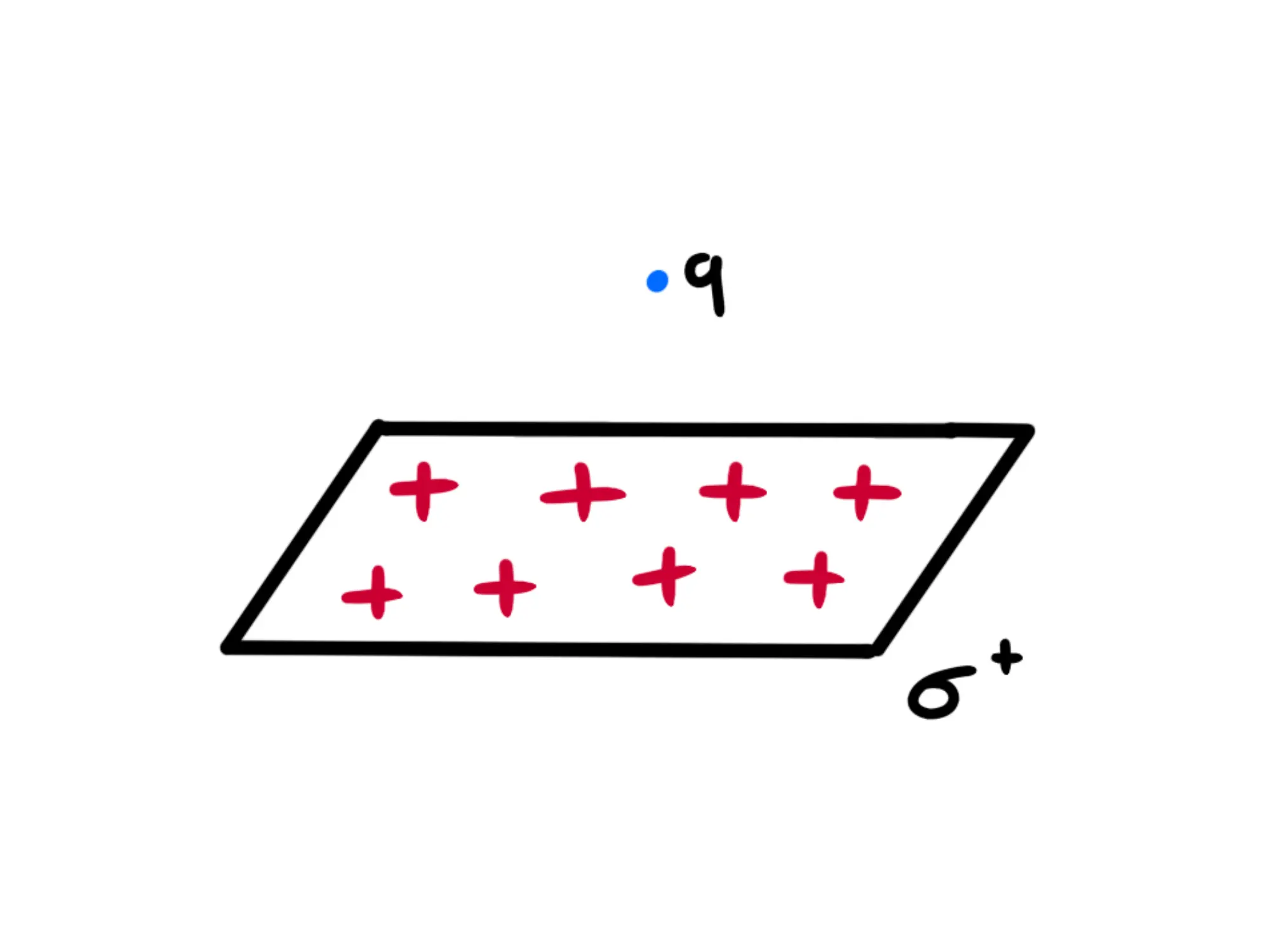
Siccome il piano genera un campo elettrico uniforme con modulo $\displaystyle { E = {\sigma \over 2\epsilon_0}, }$ la particella risentirà ovunque nello spazio di una forza con modulo $\displaystyle { Eq, }$ cioè $\displaystyle { {\sigma q\over 2\epsilon_0}, }$ con direzione perpendicolare al piano e verso rivolto verso il piano (perché è carica negativamente).

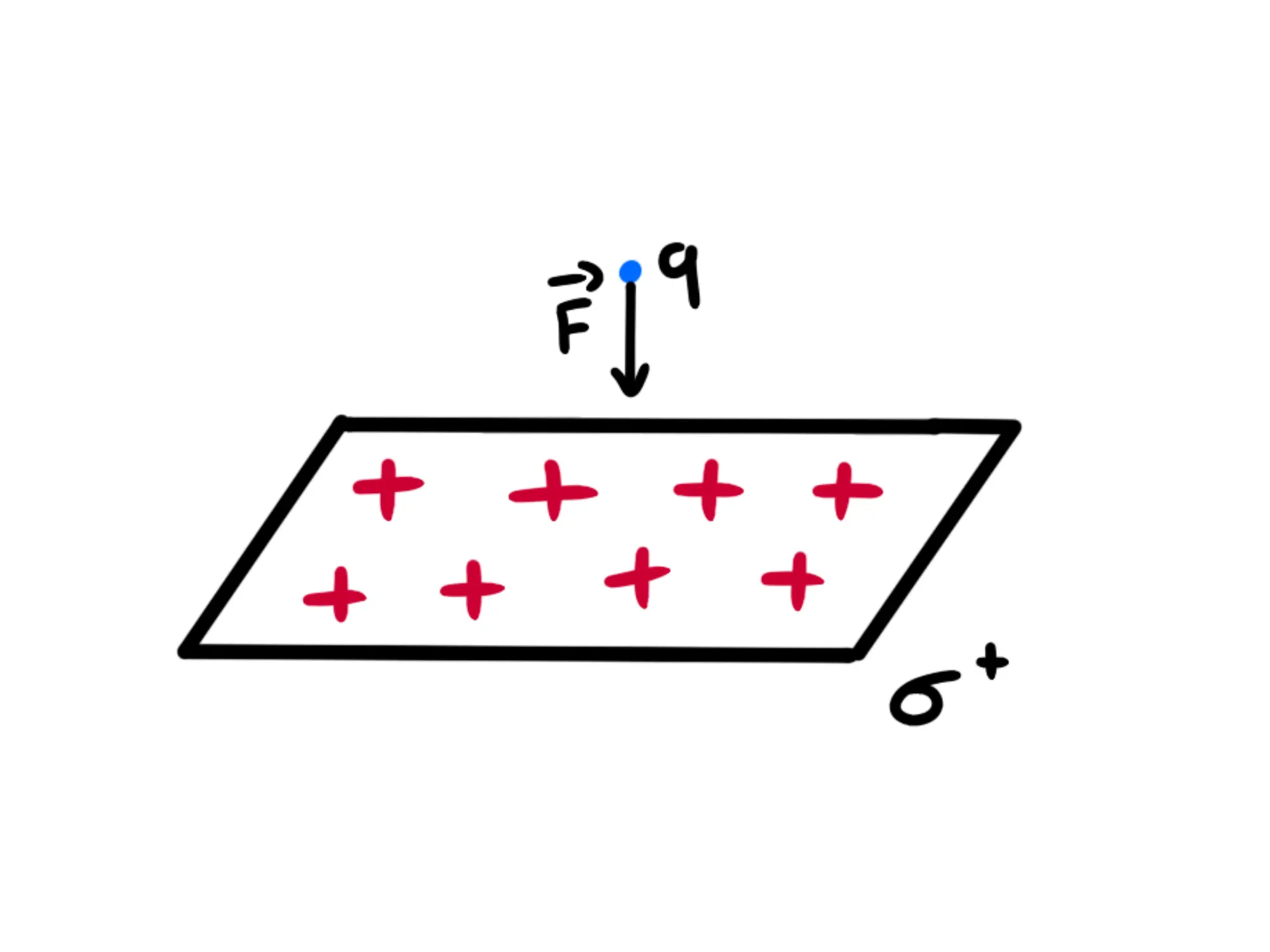
Se lascio la mia carica $\displaystyle { q }$ libera di muoversi, accelererà verso il piano. In questo modo acquisirà energia cinetica, ma non può averla presa dal nulla, quindi come ha fatto? Essa ha soltanto tramutato la sua energia potenziale elettrica in energia cinetica.

Calcoliamo quindi quanto vale quest'energia potenziale: scegliamo un sistema di riferimento in modo che l'asse delle $\displaystyle { y }$ passi per $\displaystyle { q: }$

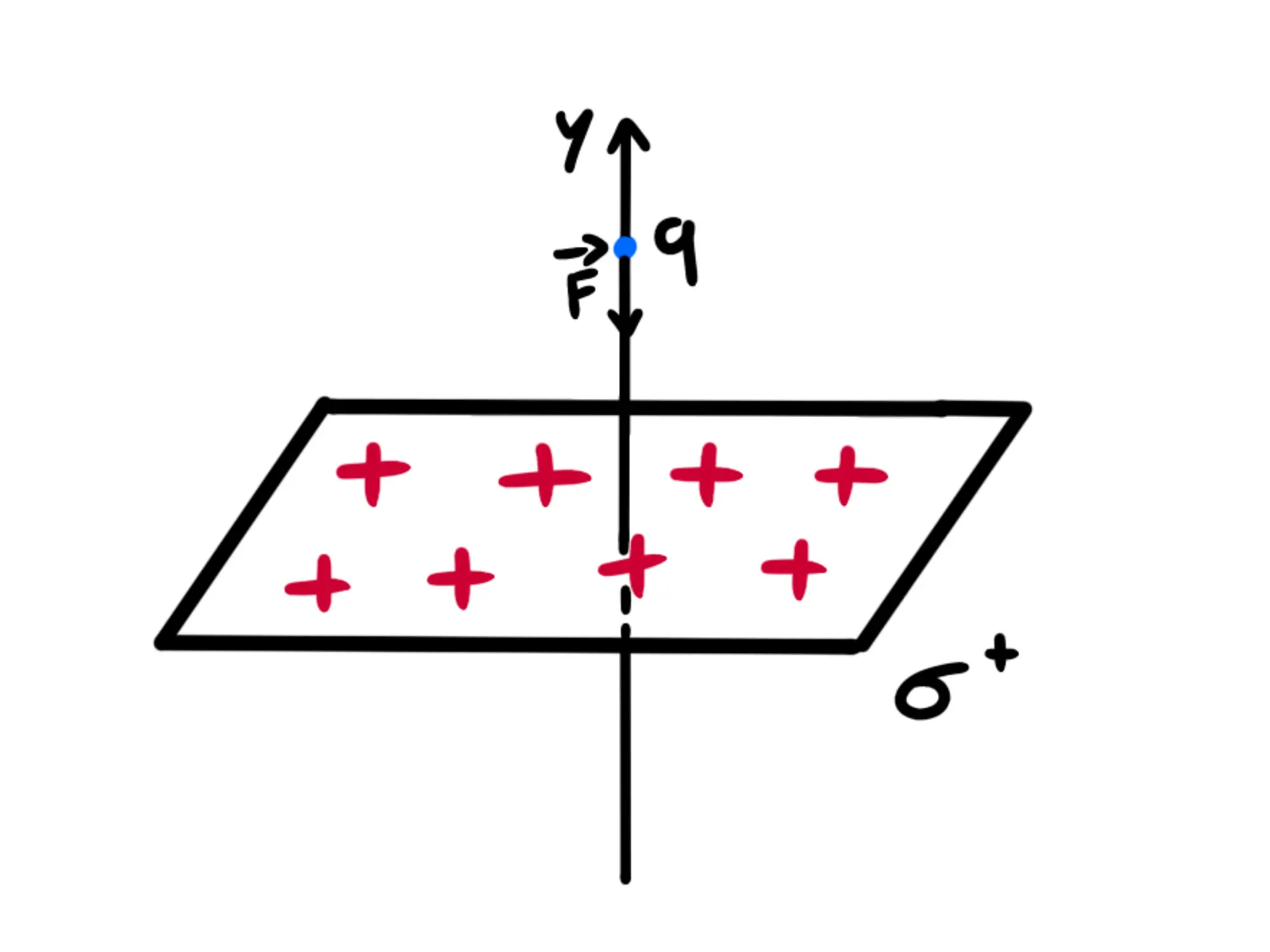
Supponiamo che la carica $\displaystyle { q }$ si trovi in un punto $\displaystyle { A }$ di altezza $\displaystyle { y_A }$ e che, lasciandola cadere, si sposti ad un punto $\displaystyle { B }$ di altezza $\displaystyle { y_B: }$

Quello che vogliamo fare, inizialmente, è trovare la differenza di energia potenziale, piuttosto che l'energia stessa. Per farlo utilizziamo il fatto che abbiamo trovato prima, cioè:

$\displaystyle { L_{F_\text{conservative}} = -\Delta U }$

L'unica forza conservativa presente è quella elettrostatica (perché stiamo ignorando la forza di gravità). Ricordandoci che $\displaystyle { L = \overrightarrow{F} \cdot \overrightarrow{s}, }$ siccome la forza e lo spostamento hanno lo stesso verso, il loro prodotto scalare sarà uguale al prodotto dei moduli, per cui:

$\displaystyle { -\Delta U }$ $\displaystyle { =L_{F_\text{conservative}} = F s = Eqs }$ $\displaystyle { = E q (y_A - y_B) = Eqy_A - Eqy_B }$

Adesso portiamo il punto $\displaystyle { B }$ sulla superficie del piano, ottendo $\displaystyle { y_B =0 }$ e quindi:

$\displaystyle { U_A - U_B = -\Delta U = Eqy_A }$

Dunque avremo:

$\displaystyle { U_A = Eqy_A + U_B }$

Dove $\displaystyle { U_B, }$ appunto, è l'energia potenziale sulla superficie del piano.

Anche l'energia potenziale elettrica, come quella gravitazionale, dipende dal proprio sistema di riferimento e quindi è sempre calcolabile a patto di una costante $\displaystyle { +C }$ che dipenderà, appunto, dalla nostra scelta del sistema di riferimento.

Quindi decidiamo di mettere lo $\displaystyle { 0 }$ dell'energia potenziale sulla superficie del piano. In questo modo avremo $\displaystyle { U_B = 0 }$ e quindi:

$\displaystyle { U_A = E q y_A }$

E in generale, mettendo lo $\displaystyle { 0 }$ in un punto qualsiasi, avrò:

$\displaystyle { U_A = Eqy_A +C }$

Dove $\displaystyle { C }$ è l'energia potenziale sulla superficie del piano nel sistema di riferimento scelto.

Notate che è molto simile alla formula per l'energia potenziale gravitazionale ( $\displaystyle { U = mgh }$ ).

Passiamo ora al caso di due cariche puntiformi:

Due cariche puntiformi

Prendiamo ora due cariche $\displaystyle { q }$ e $\displaystyle { Q. }$

La prima sentirà una forza elettrostatica in modulo $\displaystyle { F = k_0 {q Q \over r^2} }$ dove $\displaystyle { r }$ è la distanza tra le due:

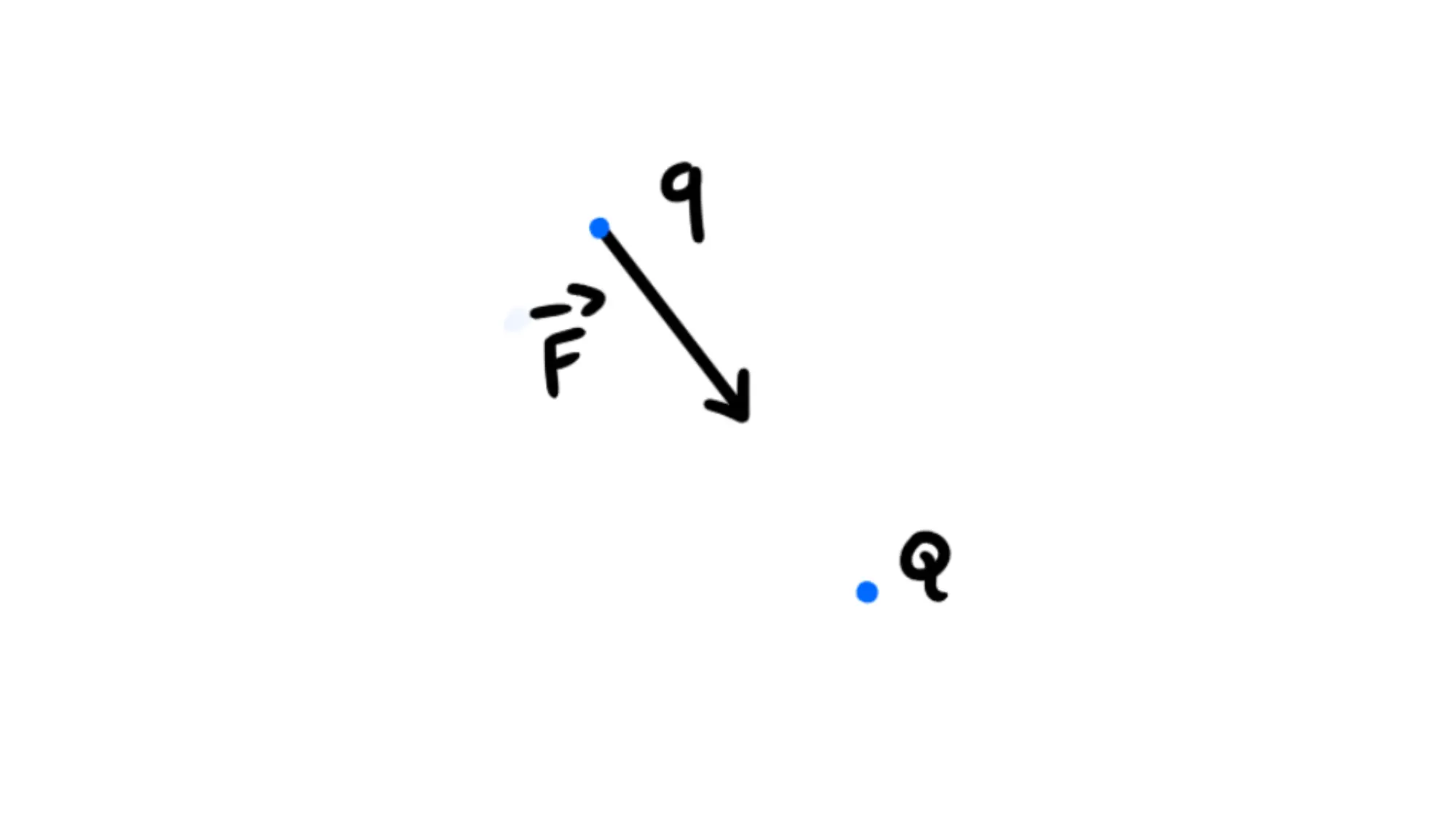
Il verso della forza dipenderà dal segno delle cariche, ma ora non importa.

Supponiamo ora che la carica la carica $\displaystyle { q }$ si sposti da un punto $\displaystyle { A }$ distante $\displaystyle { r_A }$ da $\displaystyle { Q }$ ad un punto $\displaystyle { B }$ distante $\displaystyle { r_B }$ da $\displaystyle { Q. }$

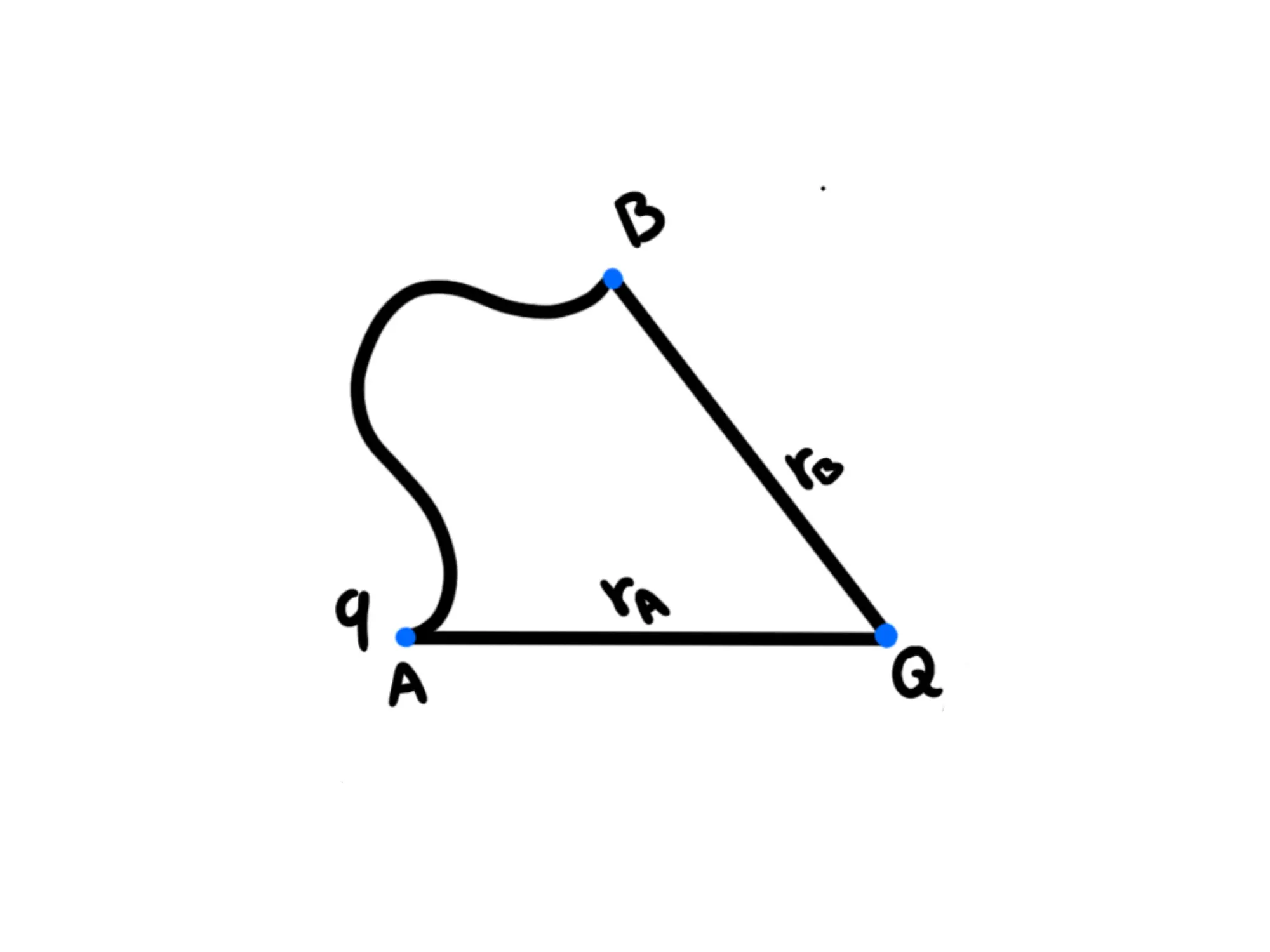
Per trovare l'energia potenziale iniziamo trovando il lavoro fatto dalle forze conservative, cioè dalla forza elettrica.

Siccome la forza elettrica è conservativa, il lavoro sarà uguale per qualsiasi percorso che scegliamo, quindi supponiamo di muoverci sulla direzione della forza finché non arriviamo ad un punto $\displaystyle { C }$ la cui distanza da $\displaystyle { Q }$ coincide con $\displaystyle { r_B }$ e poi ci spostiamo con una traiettoria circolare fino a $\displaystyle { B: }$

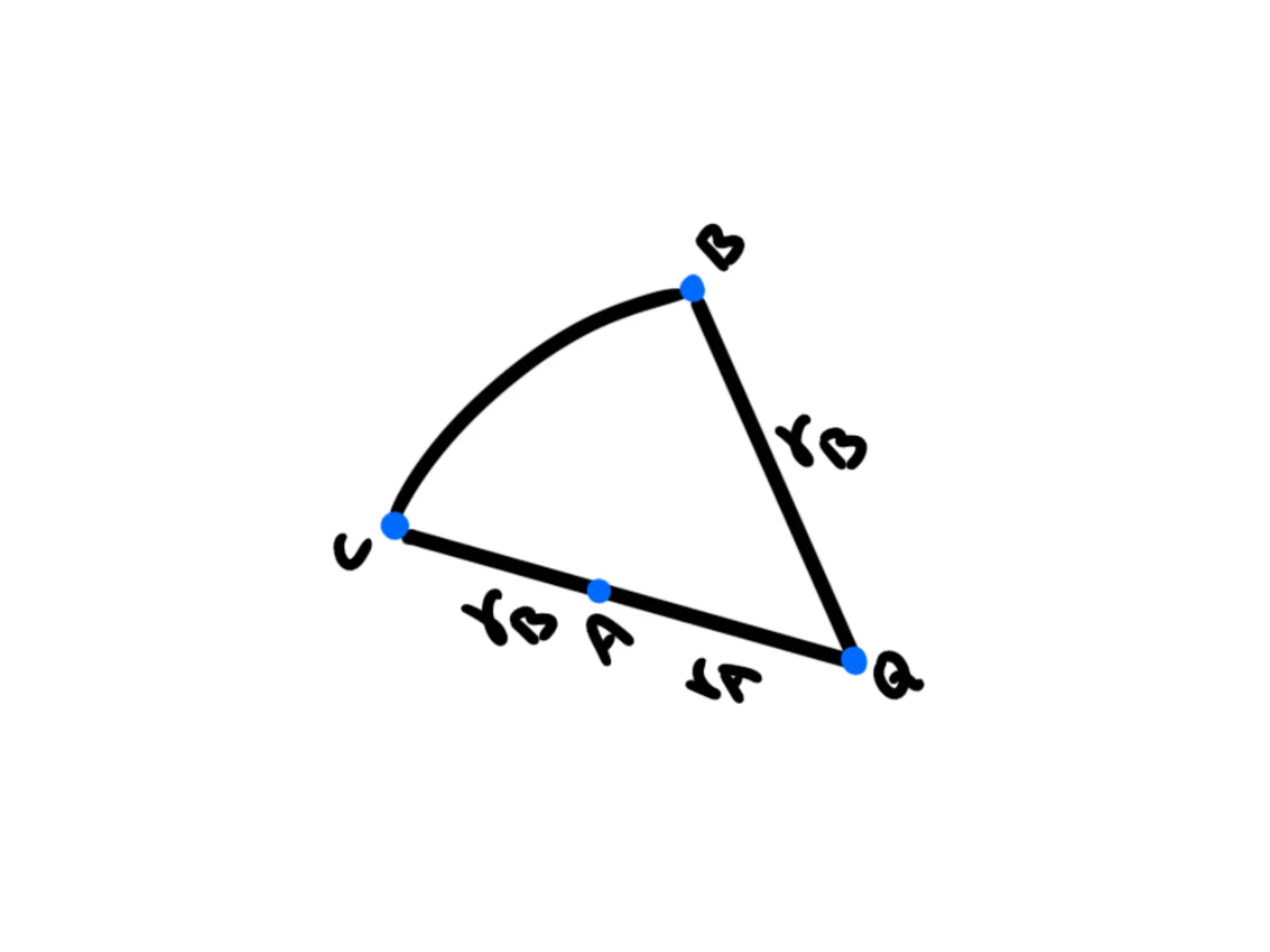
Perché abbiamo scelto questo percorso? Perché così la forza è antiparallela allo spostamento nel tratto $\displaystyle { A-C }$ ed è perpendicolare allo spostamento nel tratto $\displaystyle { C-B, }$ quindi il lavoro compiuto da $\displaystyle { C }$ a $\displaystyle { B }$ è $\displaystyle { 0 }$ e dobbiamo calcolare soltanto quello da $\displaystyle { A }$ a $\displaystyle { C: }$

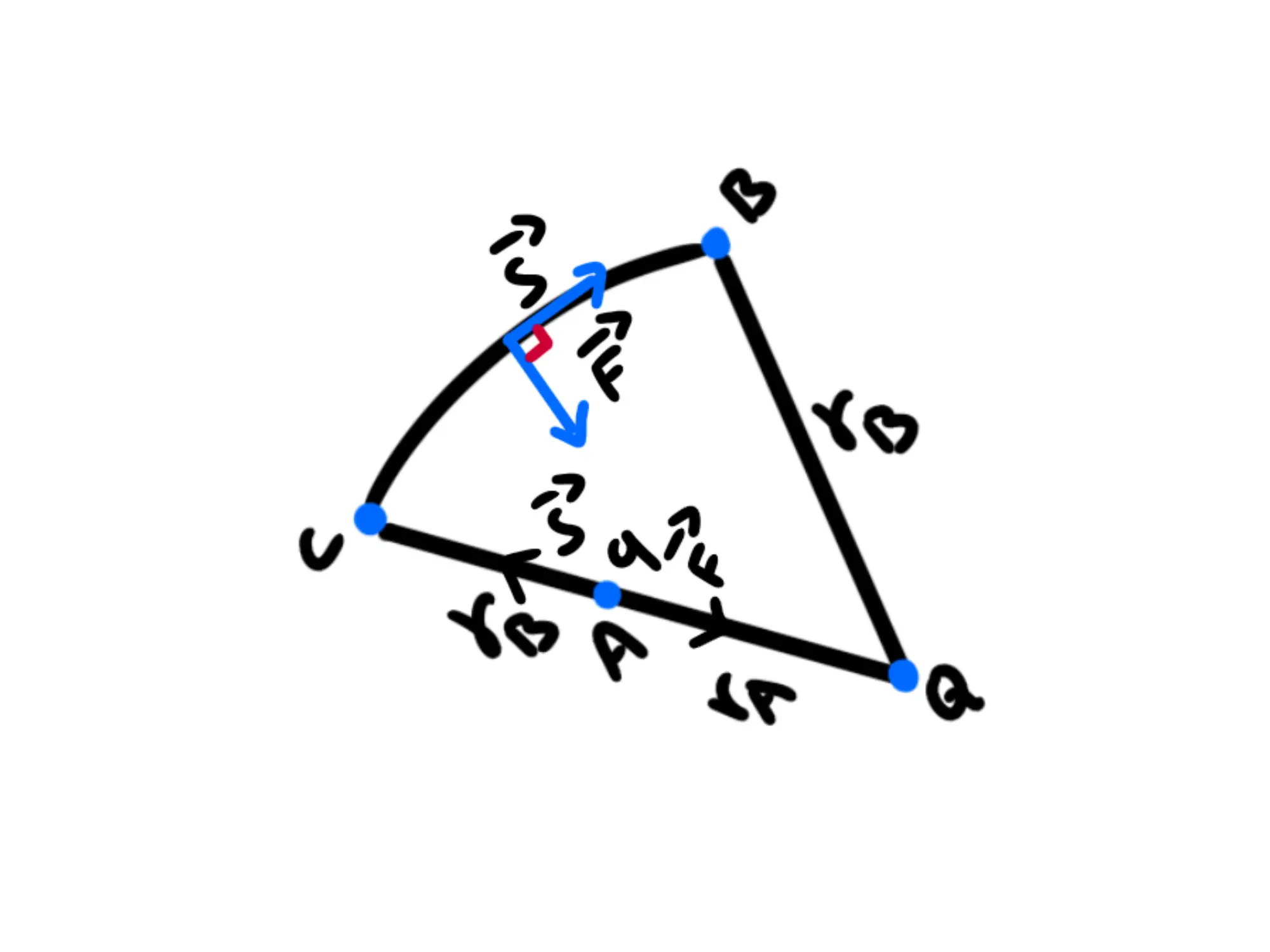
Il percorso da $\displaystyle { A }$ a $\displaystyle { C }$ è rettilineo, però il modulo della forza cambia perché dipende dalla distanza da $\displaystyle { Q. }$

Per trovare il lavoro, dunque, dobbiamo trovare il valore della forza media. Si può dimostrare che è uguale a $\displaystyle { k_0 {qQ\over r_A r_B}. }$

Dunque avremo:

$\displaystyle { L = \overrightarrow{F_{\text{media}}} \cdot \overrightarrow{s} }$ $\displaystyle { = - F_{\text{media}} \cdot s = - k_0 {qQ\over r_A r_B} (r_A - r_B) }$ $\displaystyle { = k_0 {qQ \over r_A r_B} (r_B - r_A) }$ $\displaystyle { = k_0 {qQ\over r_A} - k_0 {qQ \over r_B} }$

Ed avevamo detto che $\displaystyle { L = - \Delta U = U_A - U_B }$

Quindi:

$\displaystyle { U_A - U_ B = k_0{qQ\over r_A} - k_0{qQ\over r_B} }$

Supponiamo ora di prendere $\displaystyle { B }$ e di portarlo sempre più lontano, sempre più lontano, tanto da poter pensare che la sua distanza $\displaystyle { r_B }$ da $\displaystyle { Q }$ sia infinita.

In tal caso, $\displaystyle { k_0 {Qq\over r_B} }$ sarebbe un numero diviso per infinito, che fa $\displaystyle { 0, }$ dunque si otterrebbe:

$\displaystyle { U_A - U_B = k_0{qQ\over r_A} }$

$\displaystyle { U_A = k_0{qQ\over r_A} + U_B }$

Dove $\displaystyle { U_B }$ sarà l'energia potenziale in $\displaystyle { B, }$ cioè all'infinito.

Ci ricordiamo che noi, però, non abbiamo ancora deciso dove mettere lo $\displaystyle { 0 }$ dell'energia potenziale. Quindi possiamo scegliere di mettere lo $\displaystyle { 0 }$ all'infinito in modo che $\displaystyle { U_B }$ diventi $\displaystyle { 0. }$ In tal caso si avrebbe dunque:

$\displaystyle { U_A = k_0 {qQ \over r_A} }$

E così abbiamo finalmente ottenuto l'energia potenziale di due cariche puntiformi quando mettiamo lo $\displaystyle { 0 }$ all'infinito. Se, invece, non sappiamo dove si trova lo $\displaystyle { 0, }$ avremo:

$\displaystyle { U_A = k_0 {qQ\over r_A} + C }$

Dove $\displaystyle { C }$ sarebbe $\displaystyle { U_B, }$ cioè l'energia potenziale all'infinito.

In generale, però, potrebbero esserci più cariche, dunque studiamo anche questo caso:

Più cariche puntiformi

Cominciamo mettendo lo $\displaystyle { 0 }$ all'infinito. Perciò, se abbiamo due cariche $\displaystyle { q_1 \text{ e } q_2, }$ l'energia potenziale elettrica del sistema sarà:

$\displaystyle { U_{12} = k_0 {qQ\over r_{12}} }$

Dove $\displaystyle { r_{12} }$ è la distanza tra $\displaystyle { q_1 }$ e $\displaystyle { q_2: }$

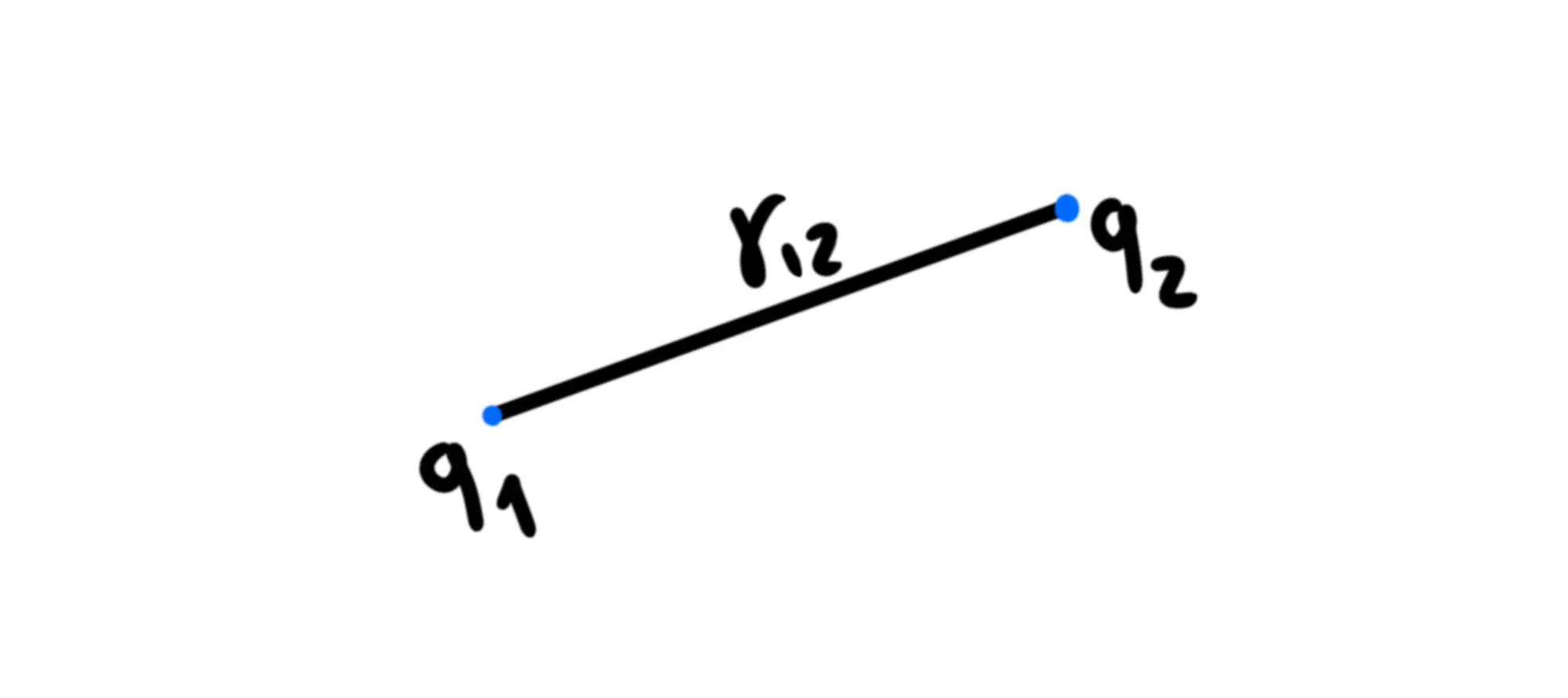
Cosa succede se introduciamo un'altra carica $\displaystyle { q_3? }$

Supponiamo di metterla all'infinito, in modo che la sua energia potenziale sia $\displaystyle { 0 }$ per poi trasportarla ad una distanza $\displaystyle { r_{13} }$ dalla carica $\displaystyle { q_1 }$ e distante $\displaystyle { r_{23} }$ dalla carica $\displaystyle { q_2: }$

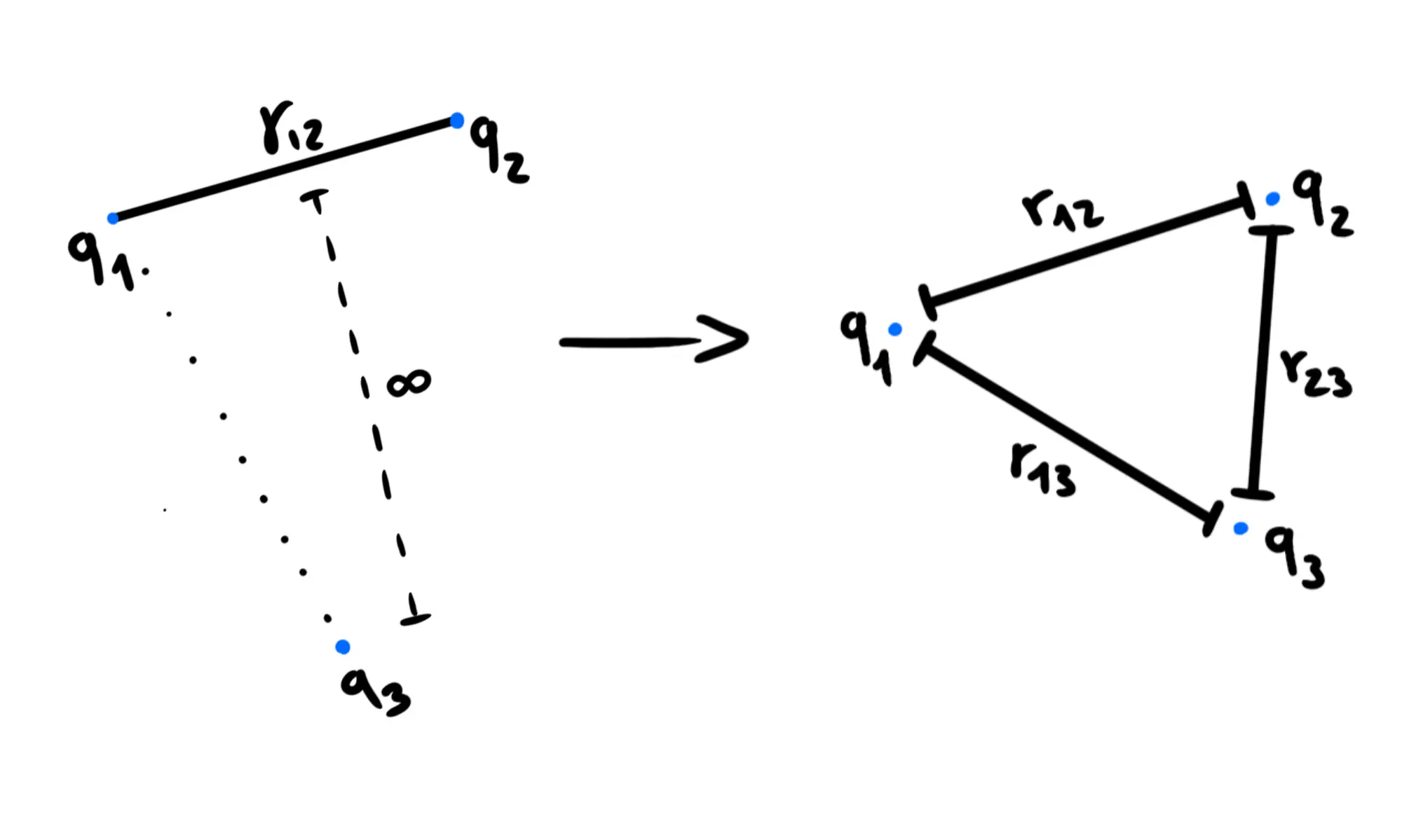
Questo processo avrà causato una variazione di energia $\displaystyle { \Delta U, }$ che sarà uguale a $\displaystyle { -L, }$ dove $\displaystyle { L }$ sta per il lavoro fatto dalla forza elettrica nello spostamento di $\displaystyle { q_3 }$ dall'infinito al punto di arrivo.

La forza che agisce su $\displaystyle { q_3 }$ è uguale alla forza elettrica esercitata da $\displaystyle { q_1 }$ più la forza esercitata da $\displaystyle { q_2. }$

Possiamo quindi vedere il lavoro totale come la somma dei lavori fatti dalle due forze. Questo significa che possiamo prima ingorare $\displaystyle { q_2 }$ e calcolare il lavoro fatto da $\displaystyle { \overrightarrow{F_{13}} }$ e poi ignorare $\displaystyle { q_1 }$ e calcolare il lavoro fatto da $\displaystyle { \overrightarrow{F_{23}}. }$

Se possiamo dunque ingnorare $\displaystyle { q_2, }$ ritorniamo al caso di prima, dove avevamo soltanto due cariche. Il lavoro fatto sarà uguale a $\displaystyle { -\Delta U }$ che abbiamo visto prima essere uguale a $\displaystyle { -{k_0{q_1 q_2 \over r_{12}}}. }$

Applicando lo stesso ragionamento per $\displaystyle { q_2 }$ e sommando insieme i due lavori, otteniamo che il lavoro totale $\displaystyle { L }$ sarà uguale a:

$\displaystyle { L = - k_0 {q_1 q_3 \over r_{13}} - k_0{q_2 q_3 \over r_{23}} }$

E quindi:

$\displaystyle { \Delta U = -L = k_0{q_1 q_3 \over {r_{13}}} + k_0 {q_2 q_3 \over r_{23}} }$

Ricordandoci che l'energia iniziale era $\displaystyle { U_i = {k_0 {q_1 q_2 \over r_{12}}}, }$ possiamo finalmente calcolare l'energia finale del sistema:

$\displaystyle { U_f = U_i + \Delta U = k_0 {q_1 q_2 \over r_{12}} + k_0{q_1 q_3 \over r_{13}} + k_0{q_2 q_3 \over r_{23}} }$

Cioè l'energia potenziale totale è uguale alla somma delle singole energie potenziale delle cariche prese a due a due.

Questo è vero per qualsiasi numero di cariche abbiamo. Se infatti prendessimo un quarta carica $\displaystyle { q_4 }$ e la ponessimo ad una distanza $\displaystyle { r_{14} }$ da $\displaystyle { q_1, }$ $\displaystyle { r_{24} }$ da $\displaystyle { q_2 }$ e $\displaystyle { r_{34} }$ da $\displaystyle { q_3, }$ applicando questo stesso ragionamento, facendo i calcoli si otterrebbe:

$\displaystyle { U_f = k_0{q_1 q_2 \over r_{12}} + k_0{q_1 q_3 \over r_{13}} + }$ $\displaystyle { k_0{q_1 q_4\over r_{14}} + k_0{q_2 q_3 \over r_{23}} + }$ $\displaystyle { k_0{q_2 q_4 \over r_{24}} + k_0 {q_3 q_4 \over r_{34}} }$

Volendo possiamo riscrivere questo risultato utilizzando la notazione della sommatoria come:

$\displaystyle { U =k_0 \sum_{i < j} ^N {q_i q_j \over r_{ij}} }$

Dove $\displaystyle { N }$ è il numero di cariche.