Partiamo subito con la definizione e poi vediamo degli esempi per chiarirla meglio.
In pratica, un numero è detto multiplo di un altro numero se e solo se è uguale a quest'ultimo moltiplicato per un altro numero naturale.
Quindi, ad esempio, è un multiplo di perché è uguale a cioè a moltiplicato per un altro numero naturale ( ).
Per lo stesso ragionamento, è un multiplo di perché è uguale a mentre è un multiplo di perché è uguale a
Dunque tutti i multipli di saranno eccetera eccetera.
Come capire, dunque, se un numero è un multiplo di un altro? Basterà fare la divisione e vedere se ci esce un numero naturale!
Se esce un numero con la virgola, allora non è un multiplo.
Quindi per verificare se è un multiplo di ci basterà fare che fa Siccome è un numero naturale, allora è un multiplo di
Mentre non è un multiplo di perché se faccio ottengo che non è un numero naturale perché ha la virgola.
Se l'aritmetica vi crea confusione e non capite cosa significa effettivamente l'essere multiplo di un numero, non vi preoccupate! Vediamo adesso una spiegazione più geometrica, e quindi più visiva, su cosa siano i multipli di un numero:
Poniamo che io disegna un mattoncino sul mio quaderno lungo quadretti:

Se io prendo mattoncini fatti così e li metto uno dopo l'altro, ottengo un unico mattoncino lungo quadretti:
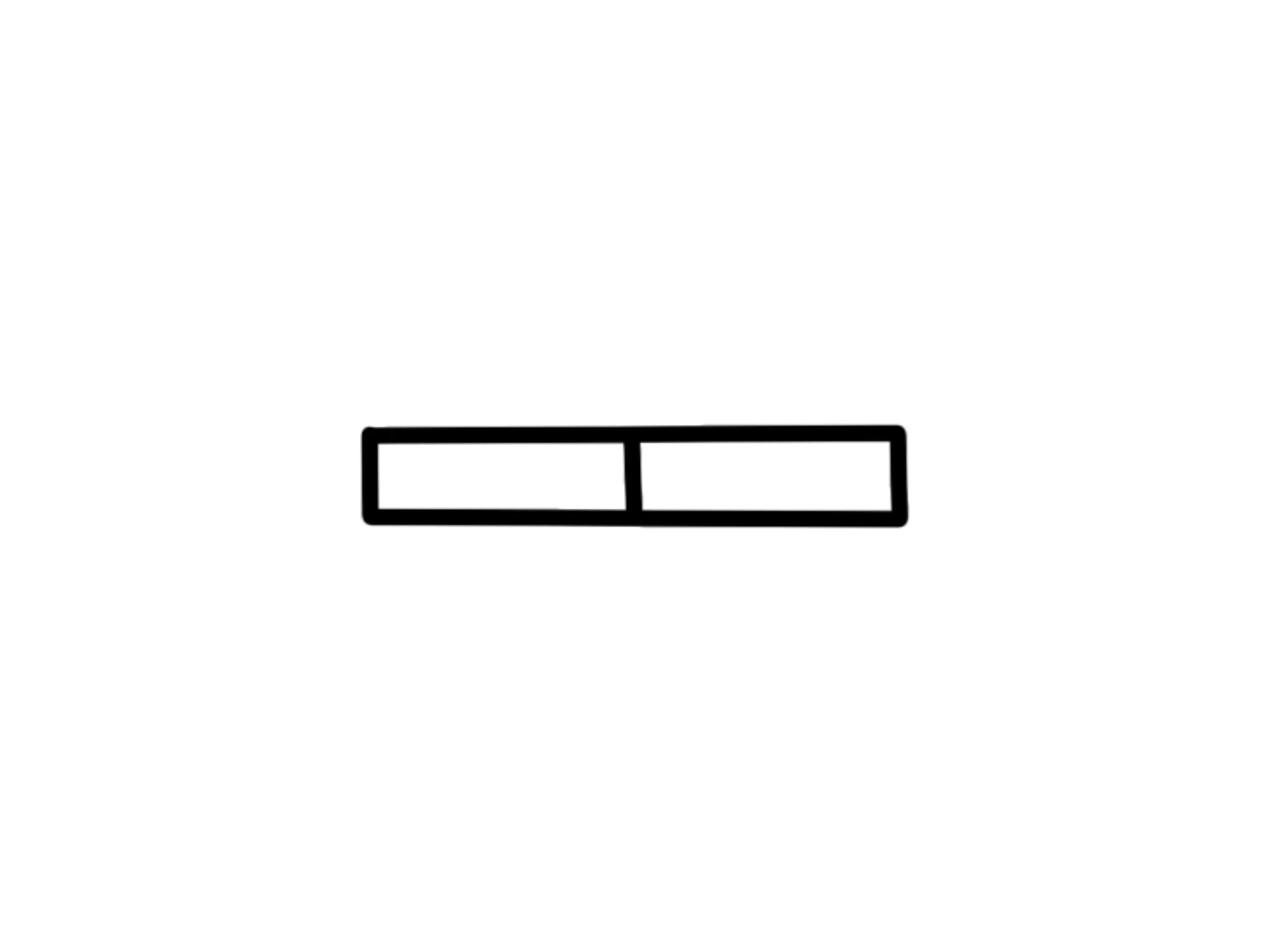
Se invece metto mattoncini, ne ottengo uno da

Cioè ogni volta che aggiungo un mattoncino, sto aggiungendo quadratini. Quindi se lo faccio volte, faccio cioè
Quindi per ottenere il numero di mattoncini totale devo fare la lunghezza del mattoncino per il numero di mattoncini che uso.
I multipli sono dunque tutte le lunghezze dei mattoncini che posso ottenere. Cioè sono tutti quei mattoncini che sono una combinazione del mattoncino.
Infatti, è un multiplo di perché un mattoncino da lo ottengo da due mattoncini da
Mentre non è un multiplo di perché se uso solo mattoncini lunghi quadretti, è impossibile disegnarne uno lungo
Quindi un numero è un multiplo di un altro se lo puoi ottenere sommando più volte quest'ultimo a sé stesso (ovvero moltiplicandolo per un numero naturale).
Potreste, però, avere una domanda: se io prendo, per esempio e lo moltiplico per ottengo quindi è un multiplo di Però anche se faccio ottengo quindi di chi è multiplo, di o di
La risposta è che lo è di entrambi! Infatti un numero può essere un multiplo di più numeri, basta che sia divisibile per essi. Quindi, è un multiplo sia di che di ma anche di di e di (e anche di ).
Quindi, se avete capito cosa sia un multiplo di un numero, per voi sarà facilissimo capire cosa sia un divisore:
Come abbiamo fatto nel capitolo precedente, vediamo prima la definizione e poi vediamo degli esempi per chiarire meglio:
Un numero è un divisore di un altro numero se la loro divisione da un numero intero.
Quindi, è un divisore di perché fa che è un numero intero.
è un divisore di perché fa che è un numero intero.
Mentre non è un multiplo di perché fa che non è un numero intero perché ha la virgola.
Infatti si chiama "divisore" perché "divide" l'altro numero in parti intere.
In altre parole, un numero è un divisore di un altro numero se quest'ultimo è un multiplo del secondo.
Cioè è un divisore di perché è un multiplo di
Quindi, usando l'esempio dei mattoncini che avevamo utilizzato prima, un numero è un divisore di un altro numero più grande se posso dividere il mattoncino grande in mattoncini della lunghezza del divisore.
Infatti posso dividere un mattoncino lungo quadratini in mattoncini da quadratini:
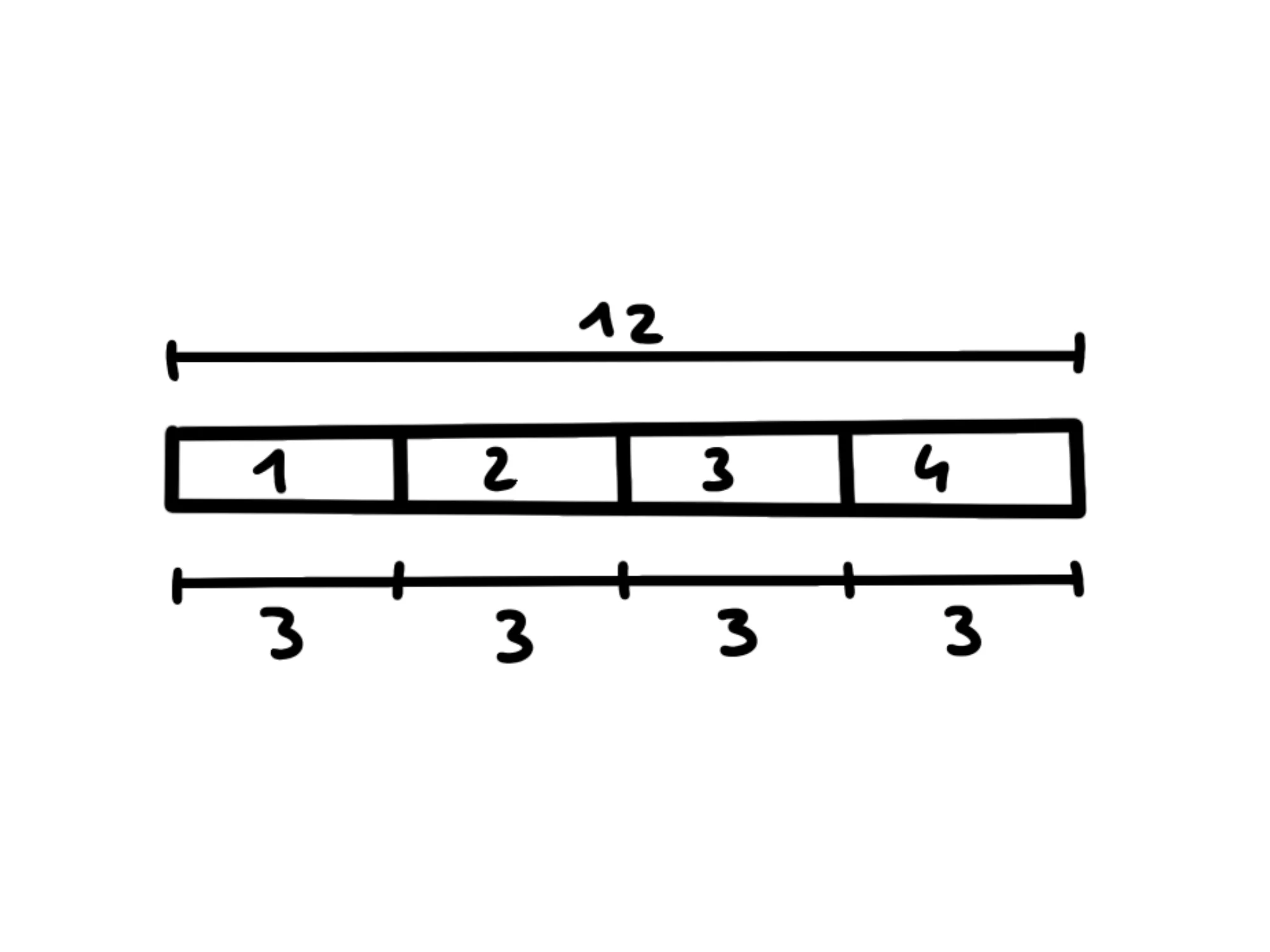
Quindi, ad esempio, i divisori di saranno e
Forse avete già notato che ci sono numeri con tantissimi divisori, come e mentre ce ne sono alcuni che ne hanno pochissimi, come e
I numeri che hanno come divisori solo e loro stessi sono chiamati numeri primi.
Quindi, ad esempio, alcuni numeri primi sono e poi ce ne sono infiniti altri. I numeri primi sono molto importanti in matematica e tra poco li rincontrerete, quindi è bene capire cosa siano.