Cosa sono?

Le disequazioni lineari a due incognite sono delle disequazioni in cui appaiono due incognite (solitamente $x$ ed $y)$ di primo grado.

Ecco alcuni esempi di disequazioni lineari a due incognite:

• $3x + 2y>0$

• $x+4y<-1$

• $13x \geq 3y + 17$

Mentre non sono disequazioni lineari a due incognite le seguenti:

• $10x>90$ perché compare una sola incognita

• $xy > 8$ perché appare un termine di secondo grado ( $xy$ , avendo due incognite moltiplicate, conta come secondo grado in questo caso)

• $y^3 + x > 7$ perché non tutte le incognite sono di primo grado.

Come risolverle

Per risolvere una disequazione di secondo grado, dobbiamo trovare tutte le coppie ordinate di numeri $(x,y)$ che la soddisfano.

Una coppia di punti soddisfa la disequazione se sostituendo i corrispettivi valori la disequazione è verificata.

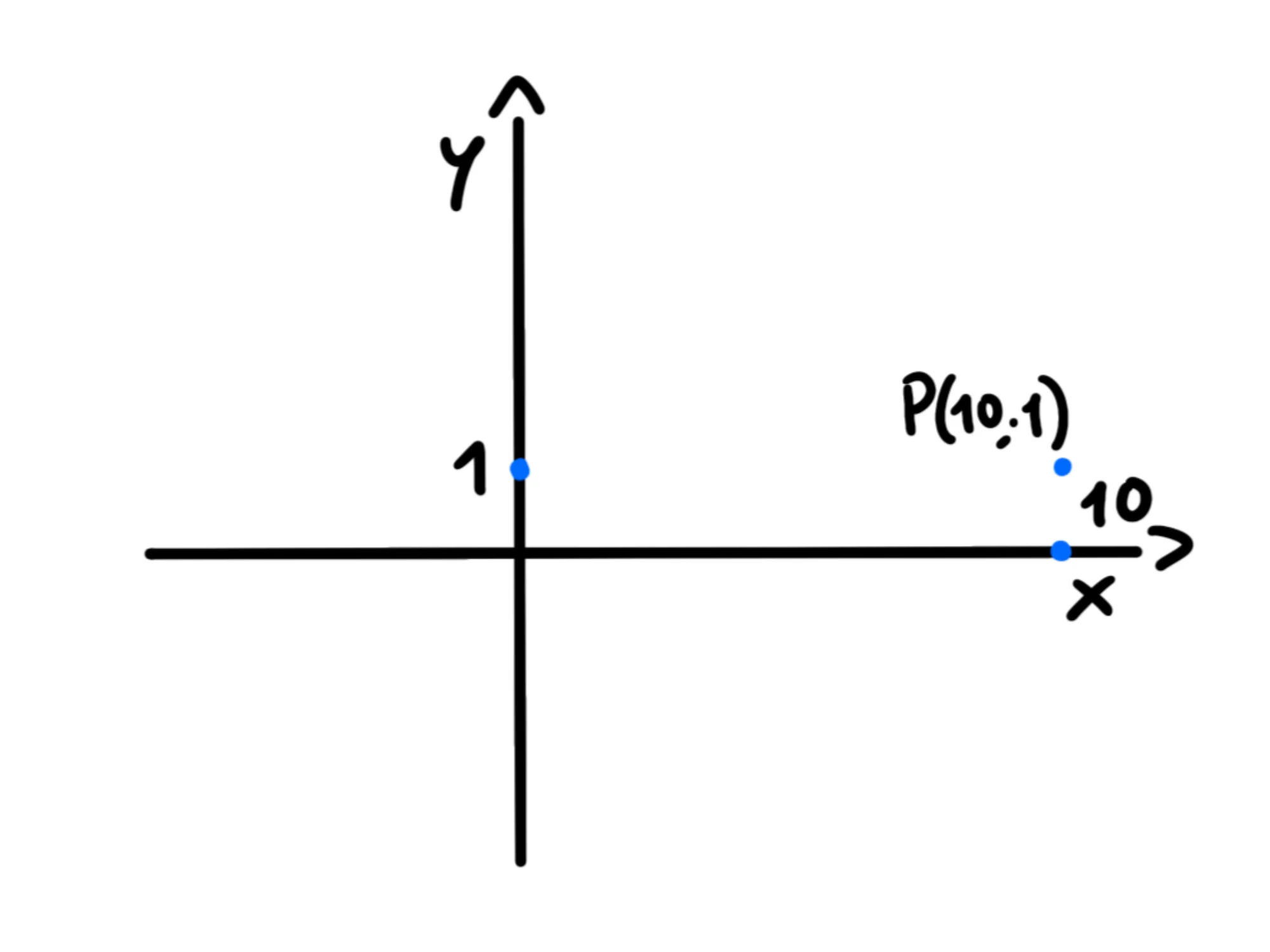
Se ad esempio abbiamo la disequazione $2x > 3y + 1,$ la coppia $(10;1)$ è una soluzione, perché $20> 3+1.$

Notiamo che possiamo collegare ogni coppia ordinata di numeri ad un punto nel piano cartesiano. Ci basta infatti prendere il punto che ha come ascissa il primo numero della coppia e come ordinata il secondo numero.

La coppia $(10;1)$ viene quindi associata al punto $P$ di coordinate $(10;1):$

Ora isoliamo la $y$ nella disequazione.

Nel nostro caso avremo:

$-3y> 1-2x$

$y< {2\over 3}x-{1\over 3}$

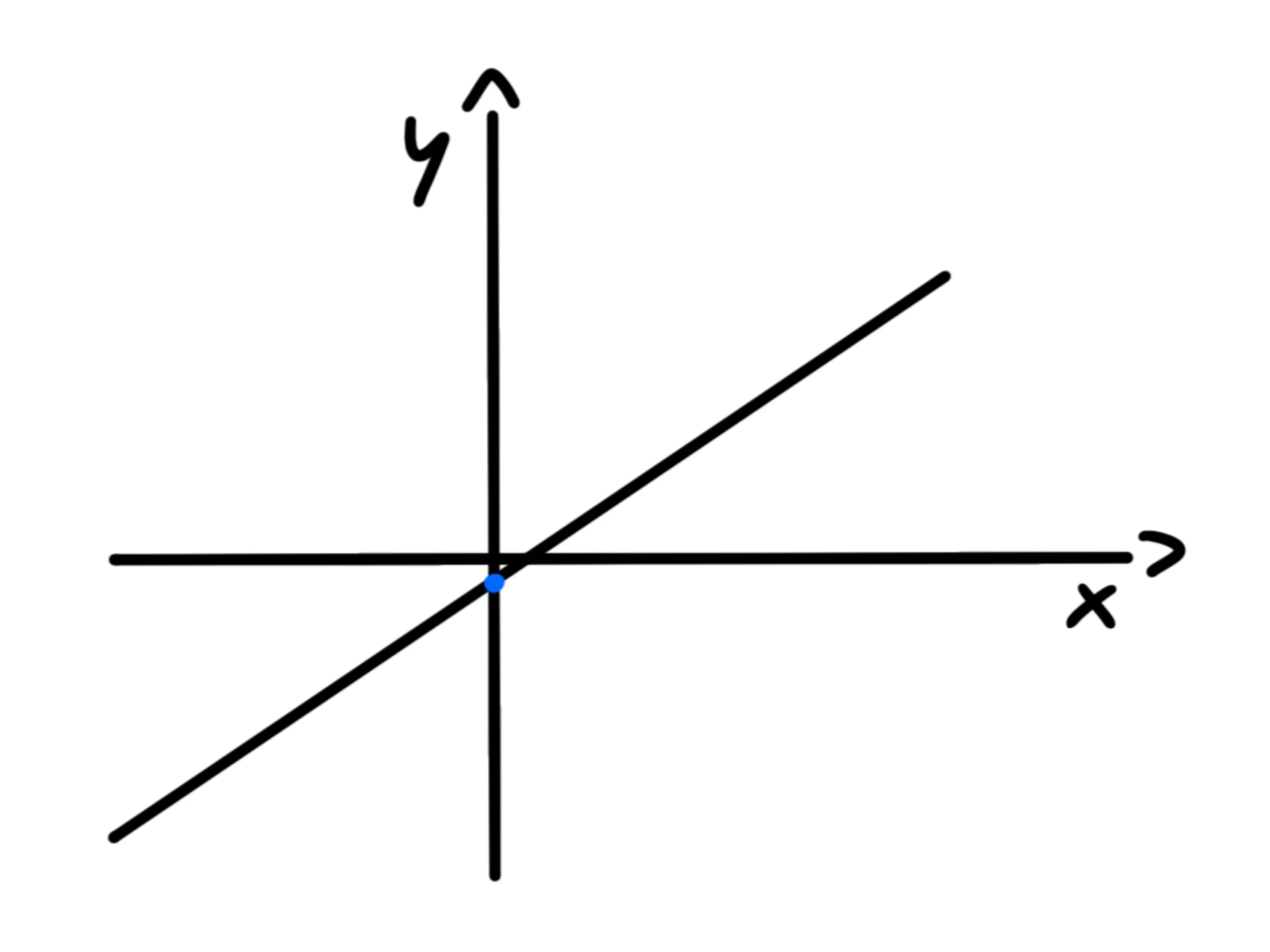
Ora vediamo cosa succede quando abbiamo l'uguaglianza invece del minore:

$y = {2\over 3} x - {1\over 3}$

Si tratta dell'equazione di una retta. Se infatti andiamo a colorare tutti i punti che soddisfano quest'equazione otteniamo:

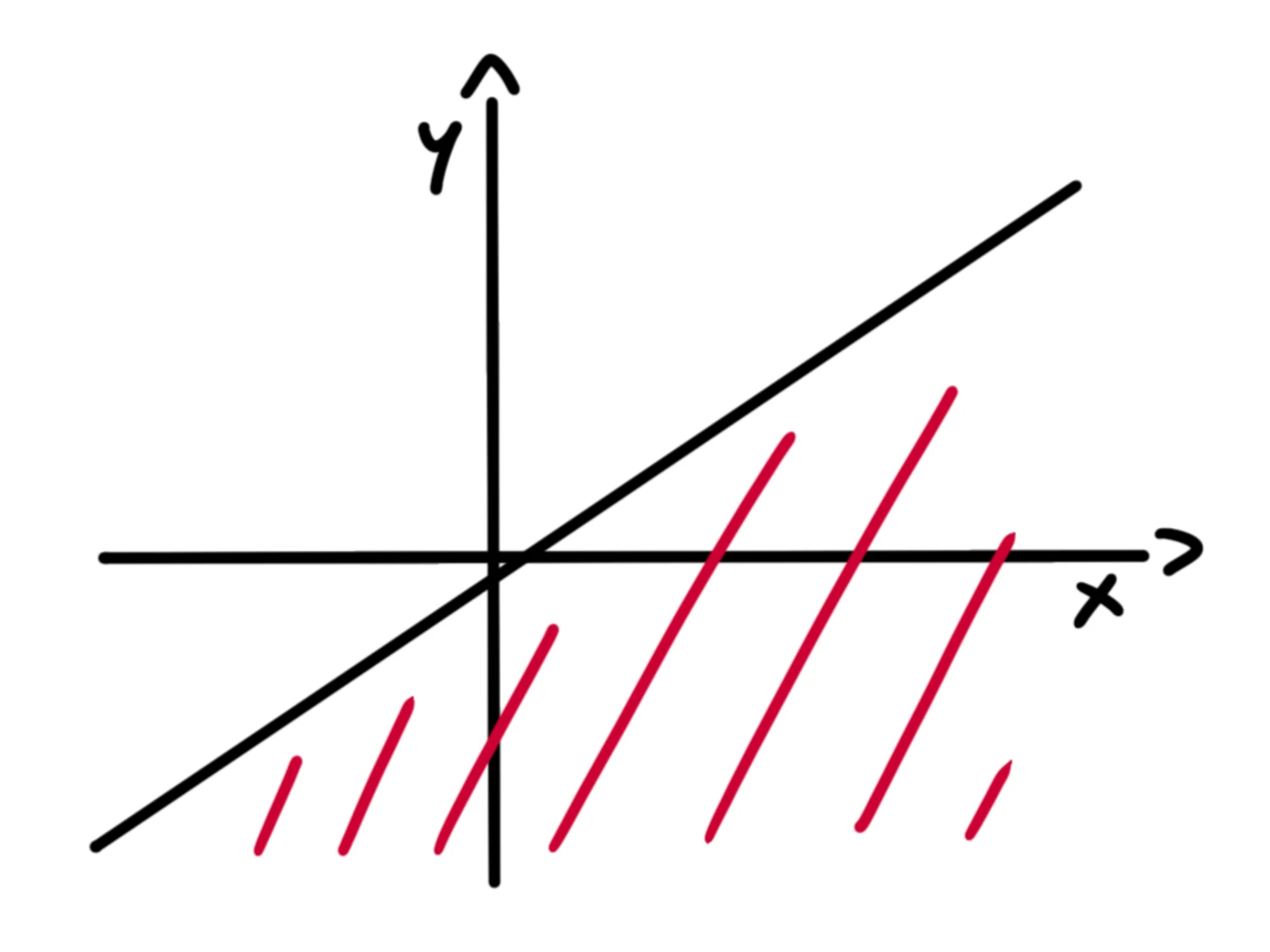
Le $y$ che verificano l'uguaglianza, quindi, si trovano sulla retta. Se chiediamo di trovare le $y$ minori ad essa, ci basta prendere le $y$ che "stanno più in basso" nel piano.

Quindi, nel nostro caso, le soluzioni alla disequazione sono tutti i punti che si trovano nel semipiano sotto alla retta $y={2\over 3}x -{1\over 3}:$

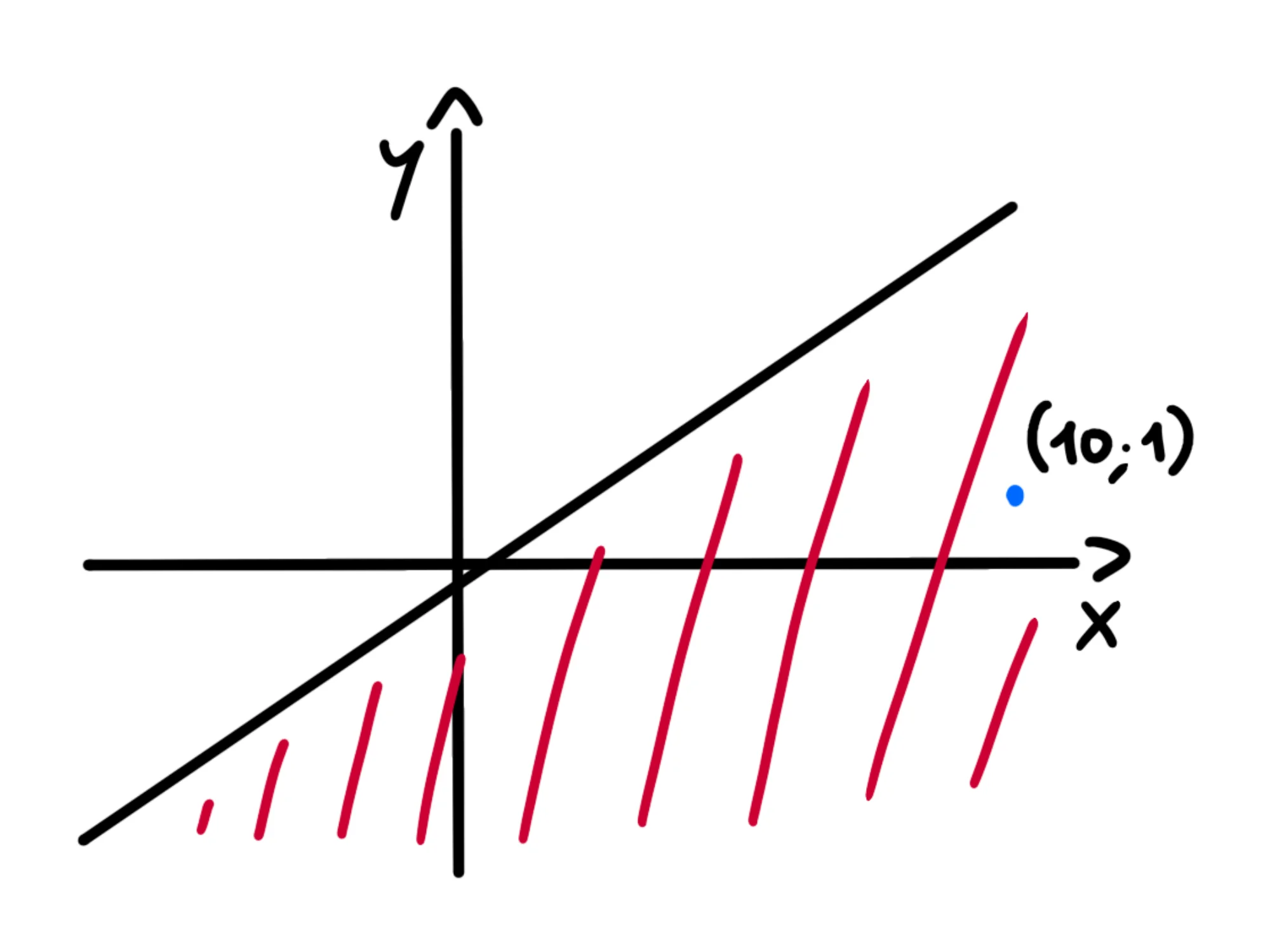
Notate che infatti il punto $(10;1)$ si trova in questa parte di piano:

Quindi, tutto quello che dobbiamo fare per risolvere questo tipo di disequazioni è isolare la $y$ e guardare alla retta associata.

A seconda del segno della disequazione, prenderemo il semipiano che si trova sopra o sotto della retta associata.

• Se abbiamo $<,$ prendiamo i valori minori, quindi prenderemo il semipiano sotto la retta.

• Se abbiamo $>,$ prendiamo i valori maggiori, dunque prenderemo il semipiano sopra la retta.

• Se abbiamo $\leq,$ prenderemo i valori minori o uguali, quindi prenderemo il semipiano sotto la retta ed anche la retta, perché pure l'uguaglianza va bene.

• Se infine abbiamo $\geq,$ prenderemo i valori maggiori o uguali, dunque prenderemo il semipiano sopra la retta ed anche la retta perché pure in questo caso ve bene l'uguaglianza.