Cos'è la corrente elettrica?

Quando abbiamo un circuito chiuso, gli elettroni cominciano a muoversi da zone a potenziale minore verso zone a potenziale maggiore (cioè dal polo negativo della batteria verso quello positivo).

Prendiamo una sezione trasversale $S$ del cavo del circuito:

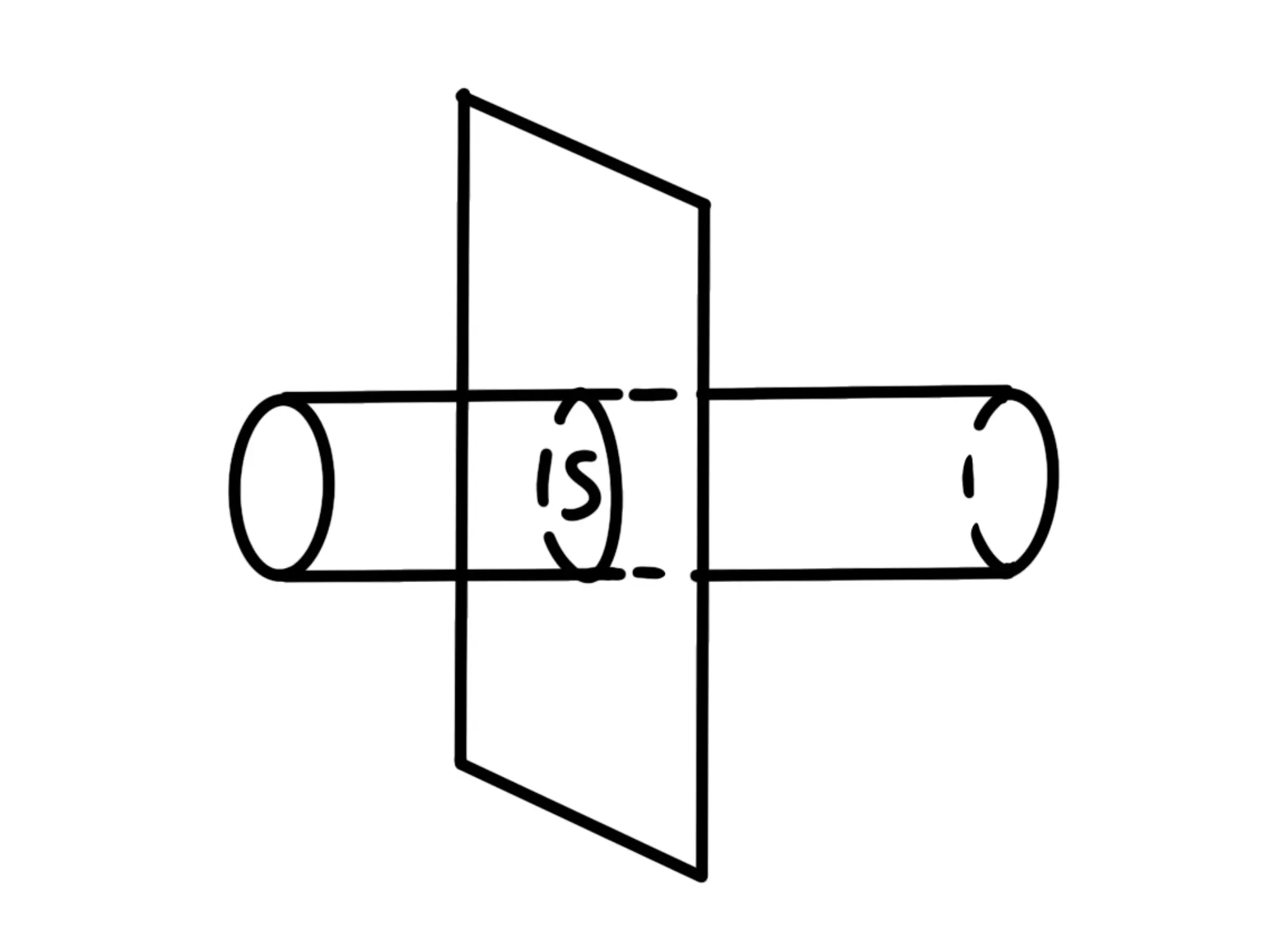
Per questa sezione, in un intervallo di tempo $\Delta t,$ passeranno un certo numero di elettroni, cioè passera una certa quantità di carica $\Delta q.$

Definiamo l intensità di corrente elettrica $i$ come il rapporto tra la carica $\Delta q$ che passa per la sezione trasversale in un intervallo $\Delta t$ e questo intervallo.

Cioè:

Questa, in realtà, si tratta dell'intensità di corrente media $i_m.$ Per ottenere l'intensità di corrente istantanea, servirebbe usare le derivate. Infatti abbiamo $i = {dq \over dt}.$

Gli elettroni che si muovono, però, non viaggiano dritti nel cavo senza impedimenti, ma vengono continuamente spinti e frenati da altri elettroni che stanno vicino a loro, per questo sono molto più lenti di quando viaggiano nel vuoto.

Noi supporremo di avere correnti stazionarie, cioè correnti in cui gli elettroni si muovono lungo il filo alla stessa velocità, chiamata velocità di deriva $v_d$ e in cui la quantità di carica che passa in ogni sezione trasversale del filo è uguale indipendentemente dallo spessore.

I primi scienziati che studiarono questi fenomeni, pensavano che la corrente elettrica fosse causata dal movimento di cariche positive, mentre noi ora sappiamo che si trattano di cariche negative.

Per questo quando scrissero le prime formule, usarono il verso della corrente opposto, cioè dal polo positivo a quello negativo. Per non dover modificare tutte queste formule, anche quando poi si è scoperto che la corrente fluiva dal polo negativo a quello positivo, si è deciso di continuare ad usare questa convenzione.

Quindi gli elettroni si muovono nel verso opposto della corrente elettrica.

Prima di calcolare la velocità di deriva, definiamo la densità di corrente:

La densità di corrente $j$ è un vettore il cui modulo è uguale al rapporto tra la corrente $i$ e l'area $S$ della sezione trasversale ed ha come direzione e verso quello della corrente elettrica.

Quindi:

Ora calcoliamo la velocità di deriva:

Sappiamo che $i = {\Delta q \over \Delta t},$ ma è difficile calcolare sperimentalmente quanta carica passa per un'unita di tempo.

È molto più facile calcolare quanti elettroni sono presenti per unità di volume del materiale con cui è fatto quel conduttore.

La quantità di carica che passa è uguale alla carica di un elettrone $e$ per il numero $N$ di elettroni che passano.

Chiamiamo $n$ la quantità di elettroni presenti in un'unità di volume, cioè $n = {N\over V}.$

Nel tempo $\Delta t$ gli elettroni percorrono un tratto $l.$

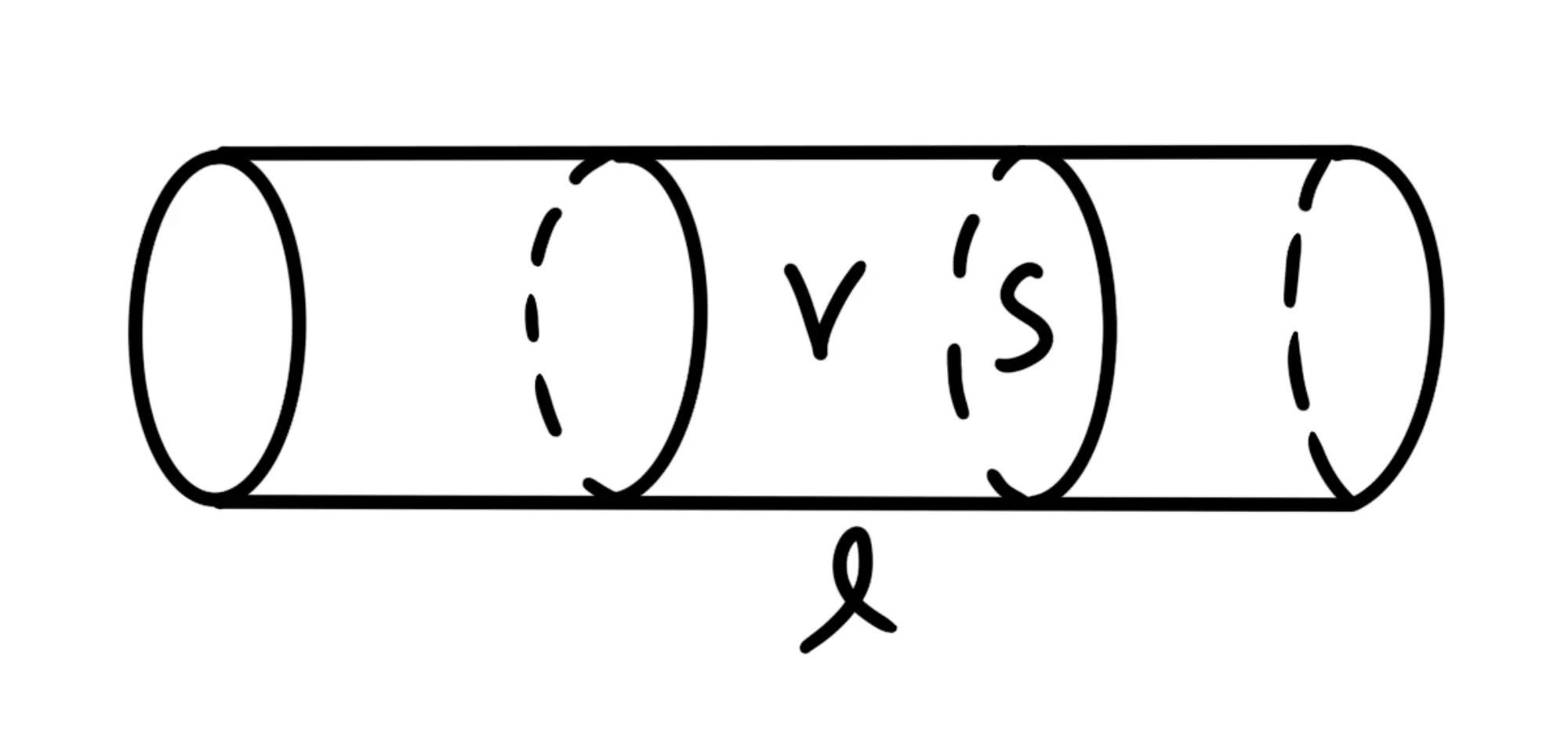
Quindi il gli elettroni che passano per la sezione trasversale nell'intervallo $\Delta t,$ sono quelli compresi nel tratto $l,$ cioè nel volume $V.$

Ma dalla definizione di $n$ abbiamo:

$N = nV$

e abbiamo detto che $\Delta q = eN,$ quindi $\Delta q = enV.$

Possiamo calcolare $V$ come $l\cdot S,$ cioè superficie di base per altezza.

In questo modo otteniamo:

$\Delta q = enlS$

Ma per la definizione di velocità, dobbiamo avere $v_d = {l \over \Delta t},$ cioè $l = v_d \Delta t.$ Sostituendo otteniamo:

$\Delta q = env_d\Delta t S$

Sostituendo il tutto nella formula per l'intensità della corrente elettrica otteniamo:

$i = {\Delta q \over \Delta t}$

$i = {env_d \Delta t S\over \Delta t}$

$i = {en v_d S}$

Dividendo entrambi i lati per $S$ otteniamo:

${i\over S} = e n v_d$

$j = env_d$

Da cui possiamo finalmente ottenere la nostra formula per la velocità di deriva: