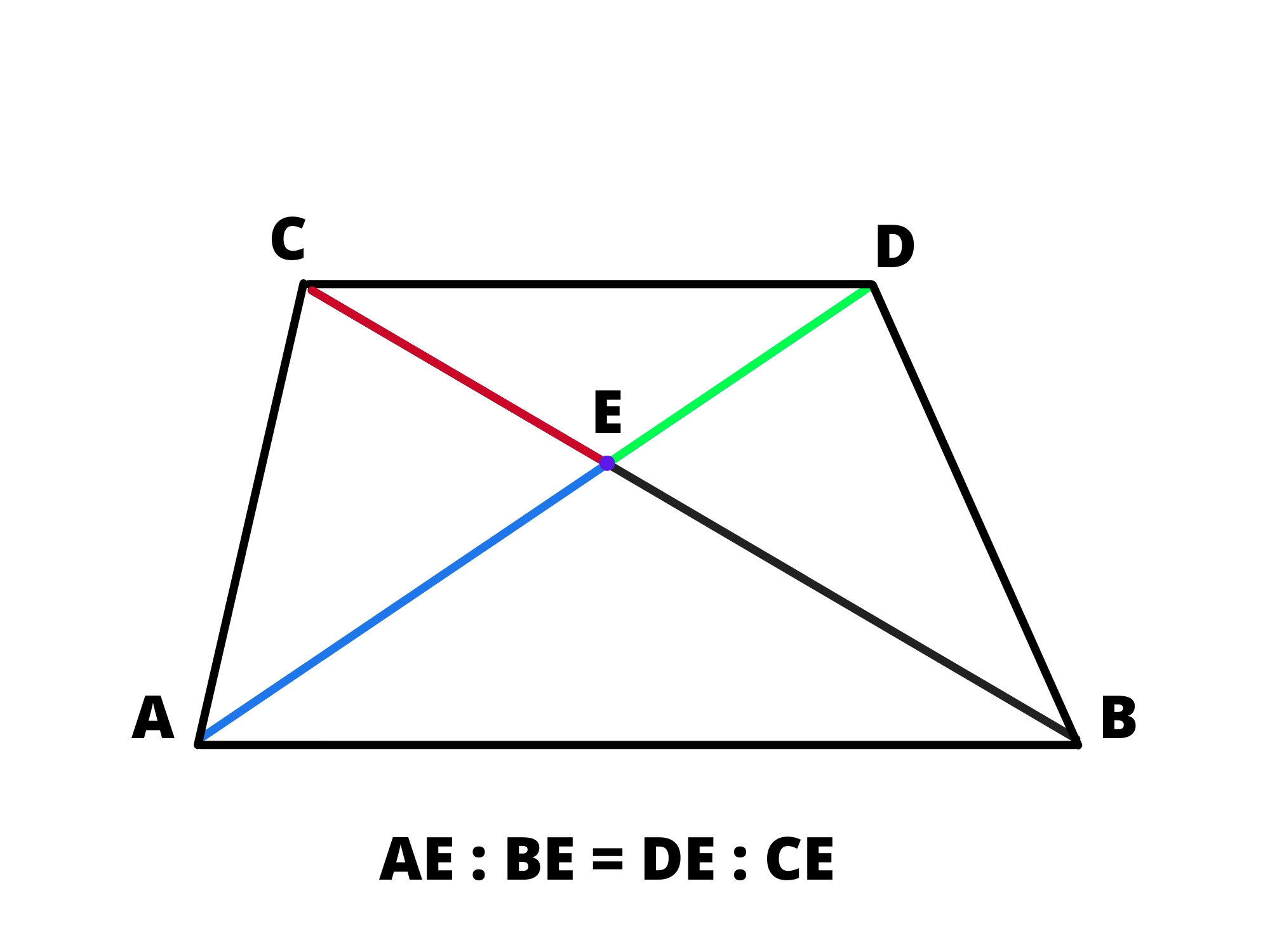
Un trapezio è un quadrilatero con due lati paralleli; i lati paralleli si chiamano basi del trapezio mentre gli altri 2 si chiamano lati obliqui.
I segmenti che uniscono i vertici opposti si chiamano diagonali.
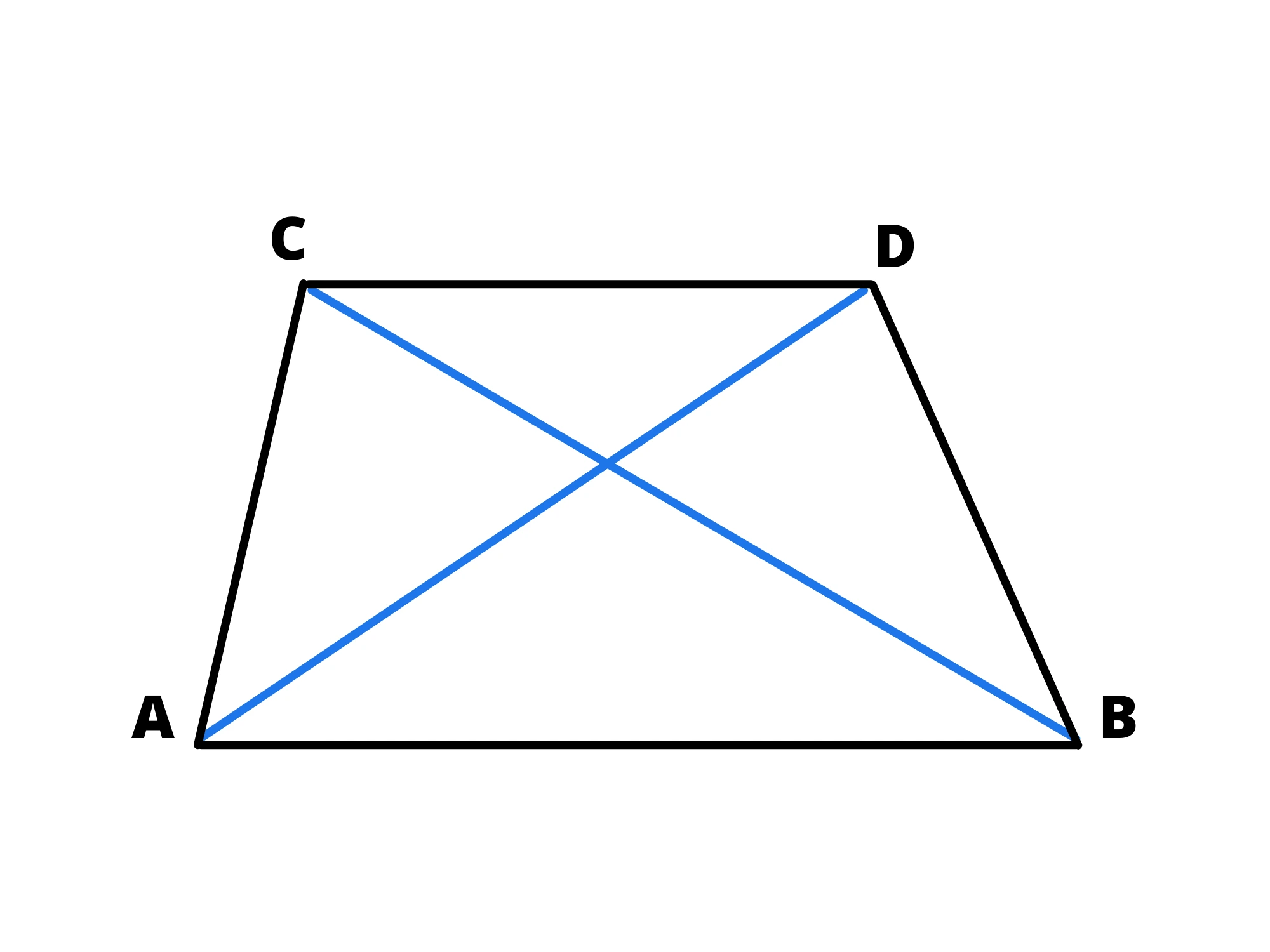
I trapezi possono essere di tipi: isosceli, rettangoli o scaleni.
Il trapezio isoscele ha i lati obliqui congruenti.
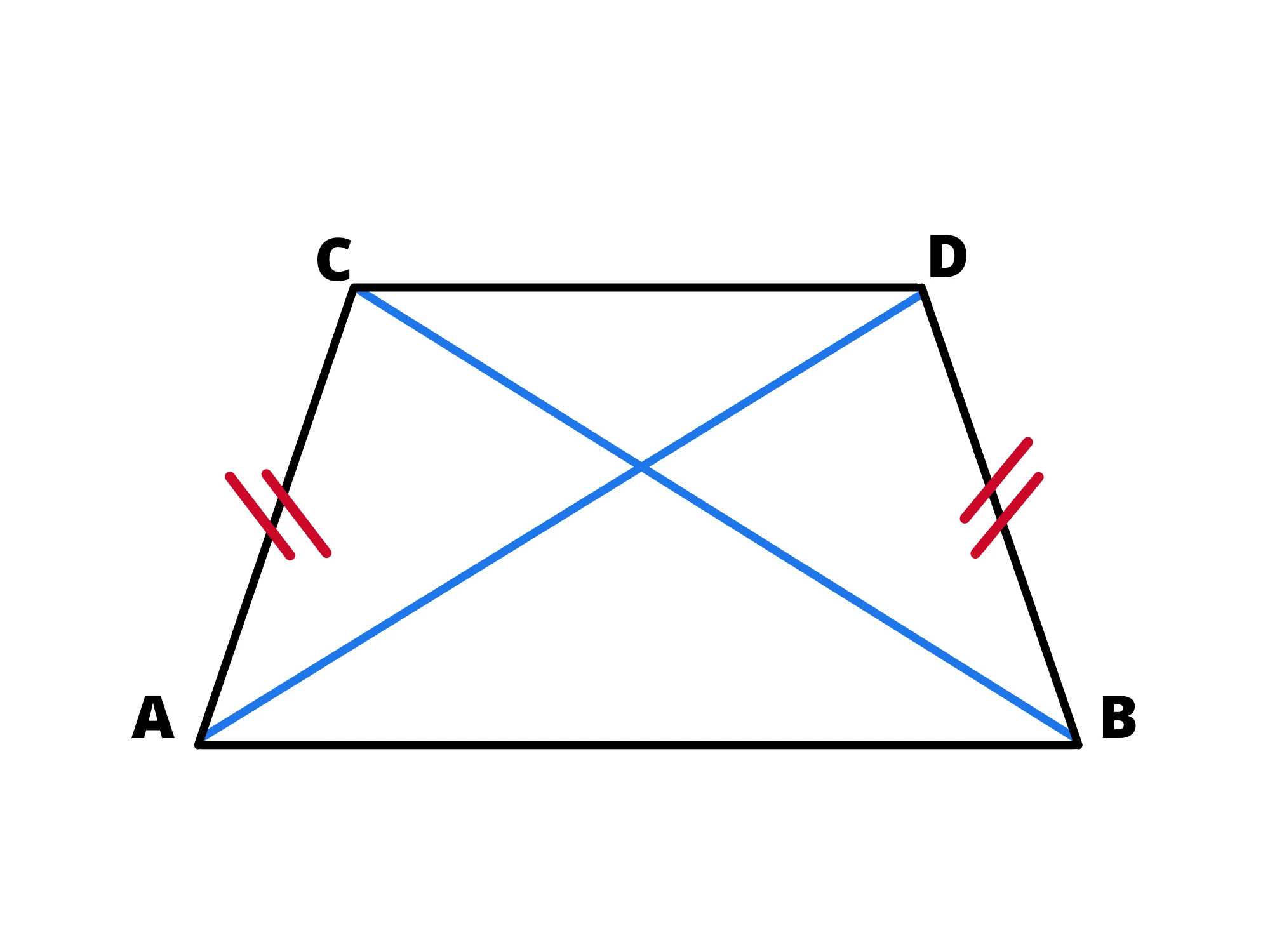
Il trapezio rettangolo ha un angolo retto.
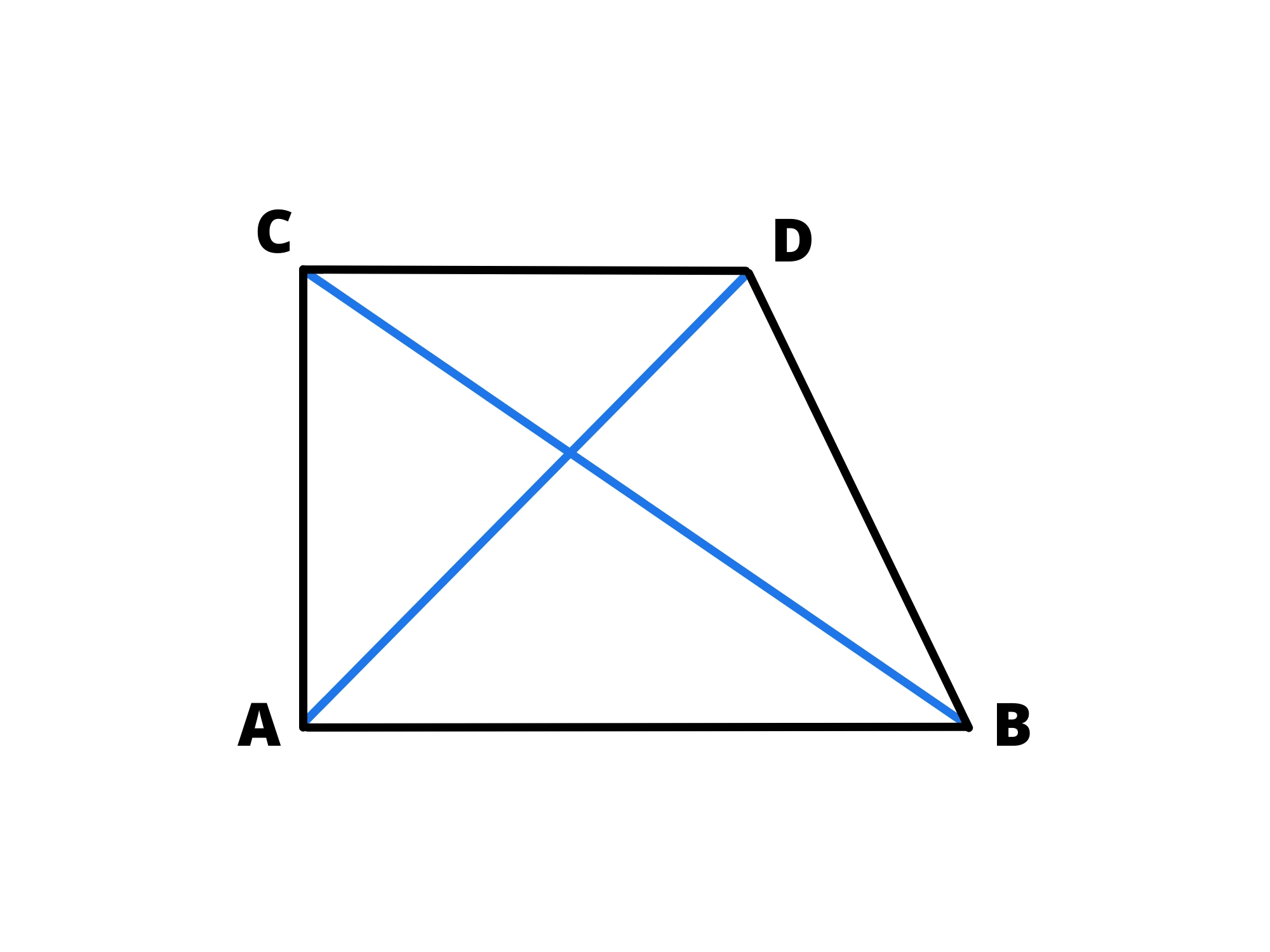
Il trapezio scaleno non ha nè lati obliqui congruenti nè un angolo retto.

Per calcolare l’area di un trapezio è necessario moltiplicare la somma delle basi per l’altezza e dividere il risultato per
Questo perché se vediamo il trapezio come triangoli aventi per base la base maggiore e la base minore del trapezio e per altezza l’altezza del trapezio possiamo calcolare l’area del trapezio sommando le aree dei triangoli:
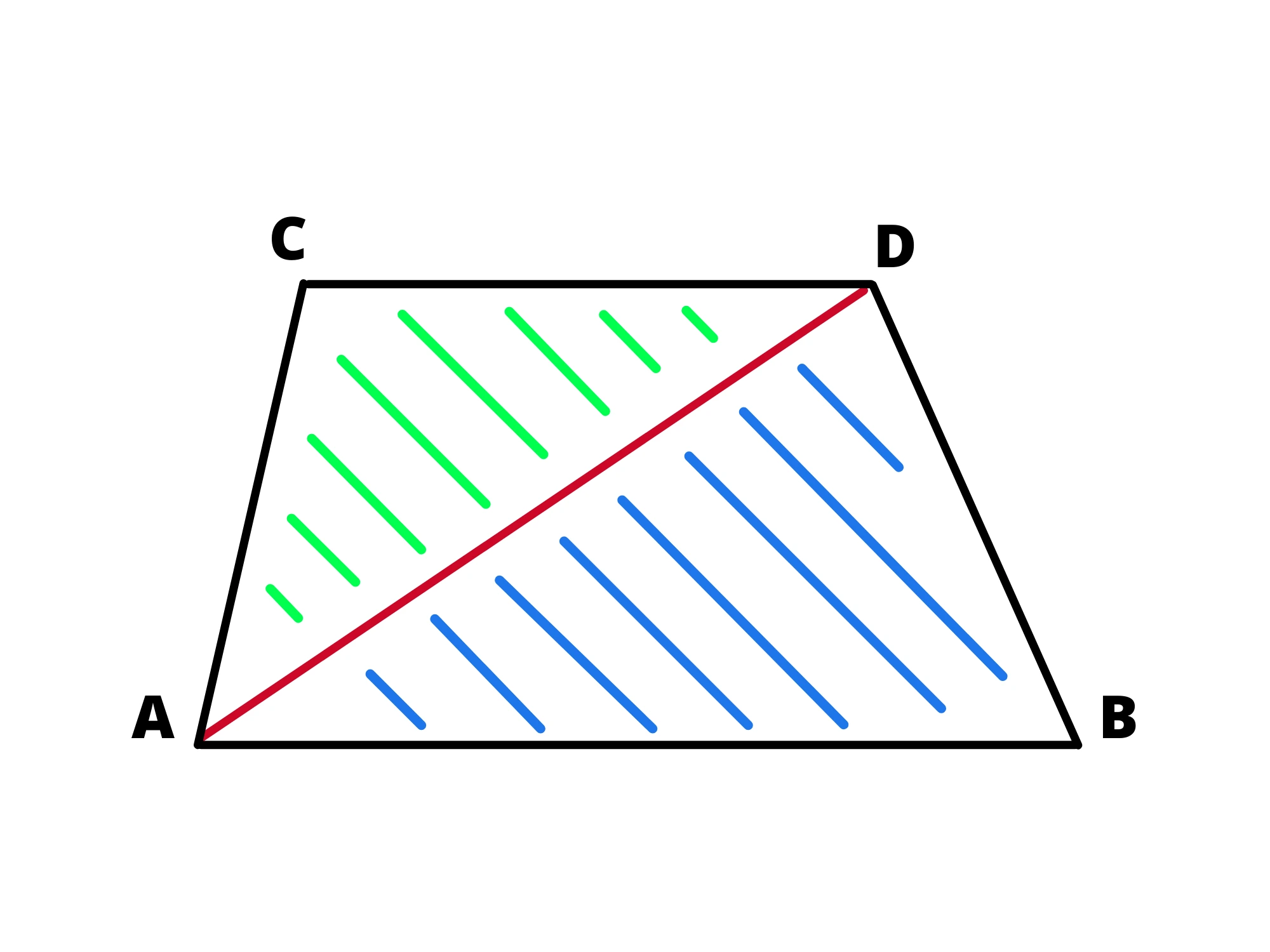
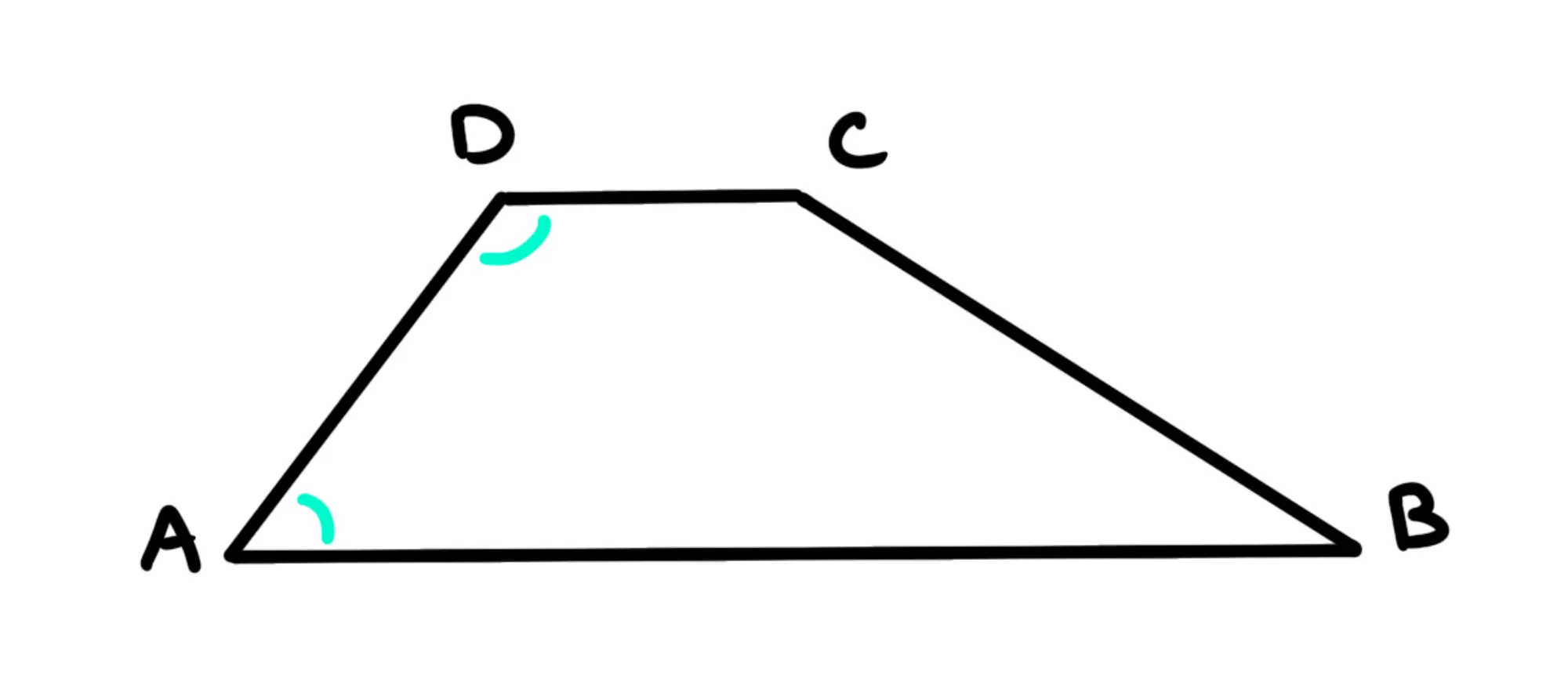
Teorema: In un trapezio, gli angoli adiacenti a un lato obliquo sono supplementari (la loro somma è ).
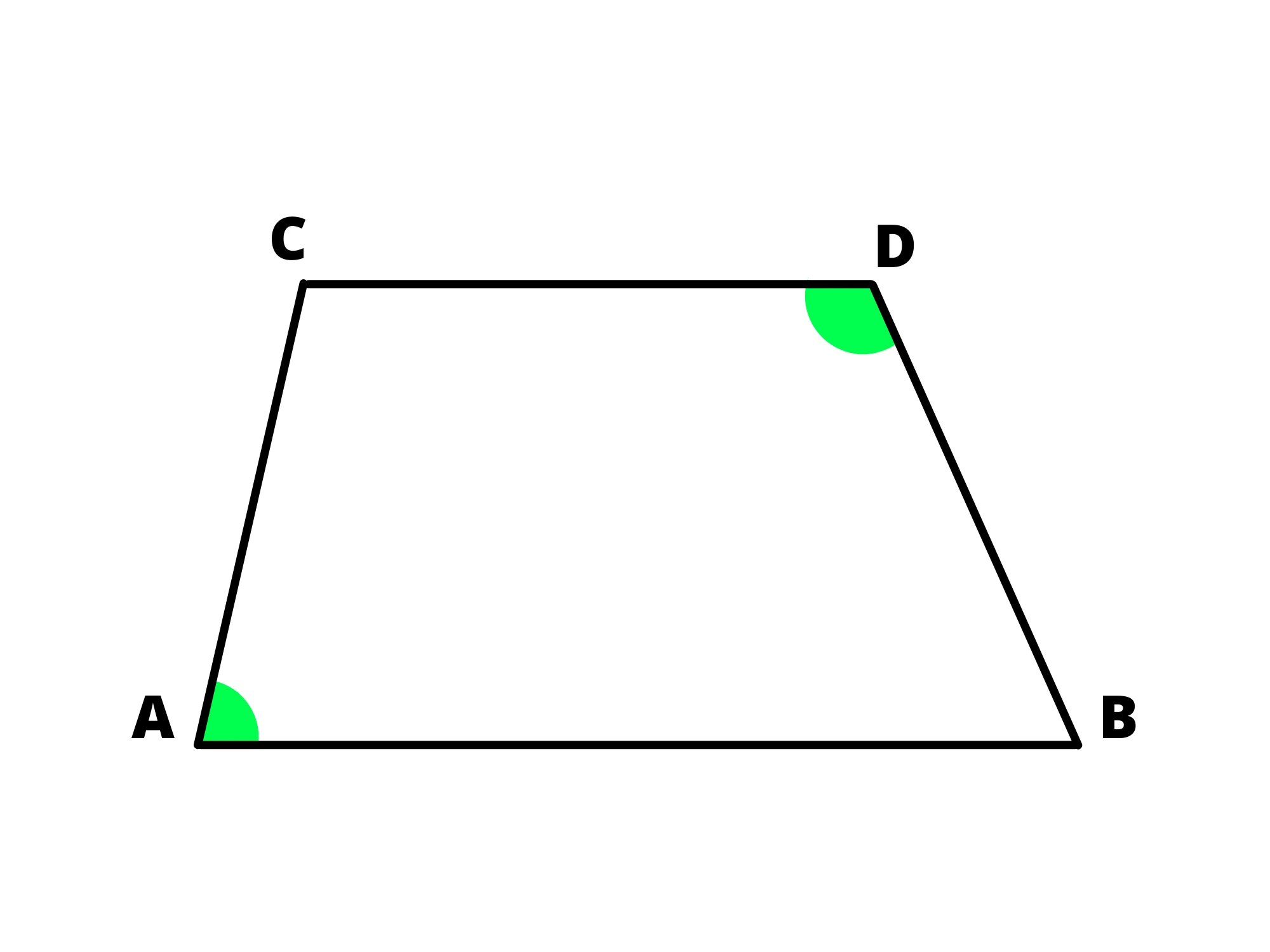
Nel trapezio isoscele anche gli angoli opposti sono supplementari.
Teorema: Le diagonali di un trapezio si tagliano in parti proporzionali.