Teoremi di analisi matematica

Regola di De l'Hopital

Può capitarvi di trovare limiti che vi restituiscono una qualche forma indeterminata. Se, infatti, otteniamo $\displaystyle { 0\over 0 }$ o $\displaystyle { {\infty \over \infty} , }$ possiamo applicare il teorema di De l'Hôpital.

Esso ci dice che, appunto, se abbiamo un limite nella seguente forma:

$\displaystyle { \displaystyle \lim_{x\to x_0} {f(x)\over g(x)} }$

E ci da come risultato un delle due forme indeterminate elencate prima, se $\displaystyle { g'(x) }$ è diverso da $\displaystyle { 0, }$ allora:

$\displaystyle { \displaystyle \lim_{x\to x_0}{f(x)\over g(x)}= \displaystyle \lim_{x\to x_0} {f'(x)\over g'(x)} }$

Cioè posso prendere la derivata al numeratore ed al denominatore senza cambiare il risultato.

Vediamo un esempio:

Risolviamo il seguente limite:

$\displaystyle { \displaystyle \lim_{x \to +\infty} {\ln(x)\over x} }$

Se vado a sostituire $\displaystyle { +\infty, }$ ottengo $\displaystyle { +\infty \over +\infty. }$ Posso quindi applicare l'Hôpital e, ricordando che $\displaystyle { {d\over dx} \ln(x) = {1\over x}, }$ ottenere:

$\displaystyle { \displaystyle \lim_{x\to +\infty} {\ln(x)\over x}= \displaystyle \lim_{x\to +\infty} {{1\over x}\over 1}= }$ $\displaystyle { \displaystyle \lim_{x\to +\infty} {1\over x}= 0 }$

L'Hôpital è uno strumento potentissimo. Ad esempio, possiamo dimostrare il limite notevole del seno che prima avevamo dovuto prendere come fatto. Infatti, siccome otteniamo $\displaystyle { 0\over 0, }$ e la derivata di $\displaystyle { x }$ è ovviamente diversa da $\displaystyle { 0 }$ in quel punto, possiamo applicare De l'Hôpital ed ottenere:

$\displaystyle { \displaystyle \lim_{x\to 0} {\sin(x)\over x} = \displaystyle \lim_{x\to 0} {\cos(x)\over 1}=1 }$

Tutto qua. Anche, ad esempio, il limite notevole della funzione esponenziale può essere dimostrato con De l'Hôpital. Le condizioni, infatti, sono soddisfatte ed otteniamo dunque:

$\displaystyle { \displaystyle \lim_{x\to 0} {e^x -1\over x}= \displaystyle \lim_{x\to 0} {e^x \over 1}= 1 }$

Equivalenze asintotiche

Se due funzioni $\displaystyle { f(x) }$ e $\displaystyle { g(x) }$ si comportano nello stesso modo quando tendono ad un certo valore, cioè se il loro rapporto è uguale a $\displaystyle { 1: }$

$\displaystyle { \displaystyle \lim_{x\to x_0} {f(x)\over g(x)}= 1 }$

Allora si dice che $\displaystyle { f(x) }$ è asintoticamente equivalente a
$\displaystyle { g(x) }$ per $\displaystyle { x }$ che tende ad $\displaystyle { x_0 }$ e si scrive solitamente:

$\displaystyle { f(x) \sim g(x) }$ per $\displaystyle { x \to x_0 }$

Se però è sottinteso a quale $\displaystyle { x_0 }$ ci stiamo riferendo, possiamo scrivere anche solo $\displaystyle { f(x) \sim g(x). }$

A cosa ci serve a noi? Solitamente nei limiti che incontriamo $\displaystyle { x }$ tende sempre agli stessi valori, a $\displaystyle { 0 }$ o a $\displaystyle { +\infty, }$ dunque se andiamo a raggruppare funzioni che si comportano nello stesso modo in quei valori, potremo risolvere molti limiti molto più facilmente.

Se ad esempio incontrassimo il seguente limite:

$\displaystyle { \displaystyle \lim_{x\to 0} {{e^{\sin(x)} - 1 \over x}} }$

Sappiamo che $\displaystyle { \sin(x) }$ si comporta come $\displaystyle { x }$ per $\displaystyle { x }$ che tende a $\displaystyle { 0, }$ dunque possiamo sostituire ed ottenere:

$\displaystyle { \displaystyle \lim_{x\to 0} {{e^{\sin(x)} - 1 \over x}}= }$ $\displaystyle { \displaystyle \lim_{x\to 0} {e^x - 1 \over x}= 1 }$

Potrete trovare limiti molto più complicati, ma il concetto è lo stesso: se dimostro che una funzione $\displaystyle { f(x) }$ è asintoticamente equivalente a $\displaystyle { g(x) }$ quando $\displaystyle { x }$ tende a $\displaystyle { x_0, }$ se poi incontro un altro limite per $\displaystyle { x }$ che tende ad $\displaystyle { x_0 }$ dove compare $\displaystyle { f(x), }$ posso sostituirla con $\displaystyle { g(x) }$ e viceversa.

Teorema di Rolle

Il teorema di Rolle enuncia che:

Se una funzione $\displaystyle { f(x) }$ è continua e derivabile in un intervallo chiuso e limitato e i valori della funzione nei limiti dell'intervallo sono uguali, allora deve esserci almeno un punto nell'intervallo in cui la derivata di $\displaystyle { f(x) }$ si annulla.

Può sembrare un po' complicato da comprendere la prima volta che lo si sente perché è un po' lungo da enunciare, però dopo averci pensato un po' risulta molto intuitivo, per questo viene solitamente studiato a scuola.

Dunque, prendiamo una funzione $\displaystyle { f(x) }$ che assume lo stesso valore negli estremi di un intervallo chiuso e limitato. Il caso più semplice è che si tratti di una funzione costante:

Siccome la derivata di una funzione costante è, appunto, sempre $\displaystyle { 0, }$ il teorema è verificato.

Supponiamo quindi, che la funzione stia aumentando ad $\displaystyle { a: }$

Siccome si tratta di una funzione continua, se sta aumentando, per tornare al valore di partenza, dovrà diminuirlo. Questo però significa che all'inizio la derivata di $\displaystyle { f(x) }$ è positiva e poi diventa negativa.

Dunque, se da positiva deve diventare negativa, dovrà per forze passare per $\displaystyle { 0 }$ e dunque il teorema è verificato.

Lo stesso esatto ragionamento si applica nel caso in cui la funzione stia diminuendo ad $\displaystyle { a. }$

Teorema di Lagrange

Il teorema di Lagrange viene spesso visto come una generalizzazione del teorema di Rolle che abbiamo visto prima. Infatti, esso enuncia che:

Se una funzione $\displaystyle { f(x) }$ è continua e derivabile in un intervallo chiuso e limitato $\displaystyle { [a,b], }$ allora esiste un punto c in quell'intervallo tale che:

Il rapporto che troviamo a destra, per definizione, altro non è che il coefficiente angolare della retta passante per i punti $\displaystyle { (a;f(a)) }$ e $\displaystyle { (b;f(b)). }$

Per la definizione di derivata, poi, $\displaystyle { f'(c) }$ è il coefficiente angolare della retta tangente alla funzione $\displaystyle { f(x) }$ in $\displaystyle { c. }$

Quindi, dire che questi due coefficienti angolari sono uguali, vuol dire, per la definizione di parallelismo, che la tangente a $\displaystyle { c }$ è parallela alla retta passante per quei due punti:

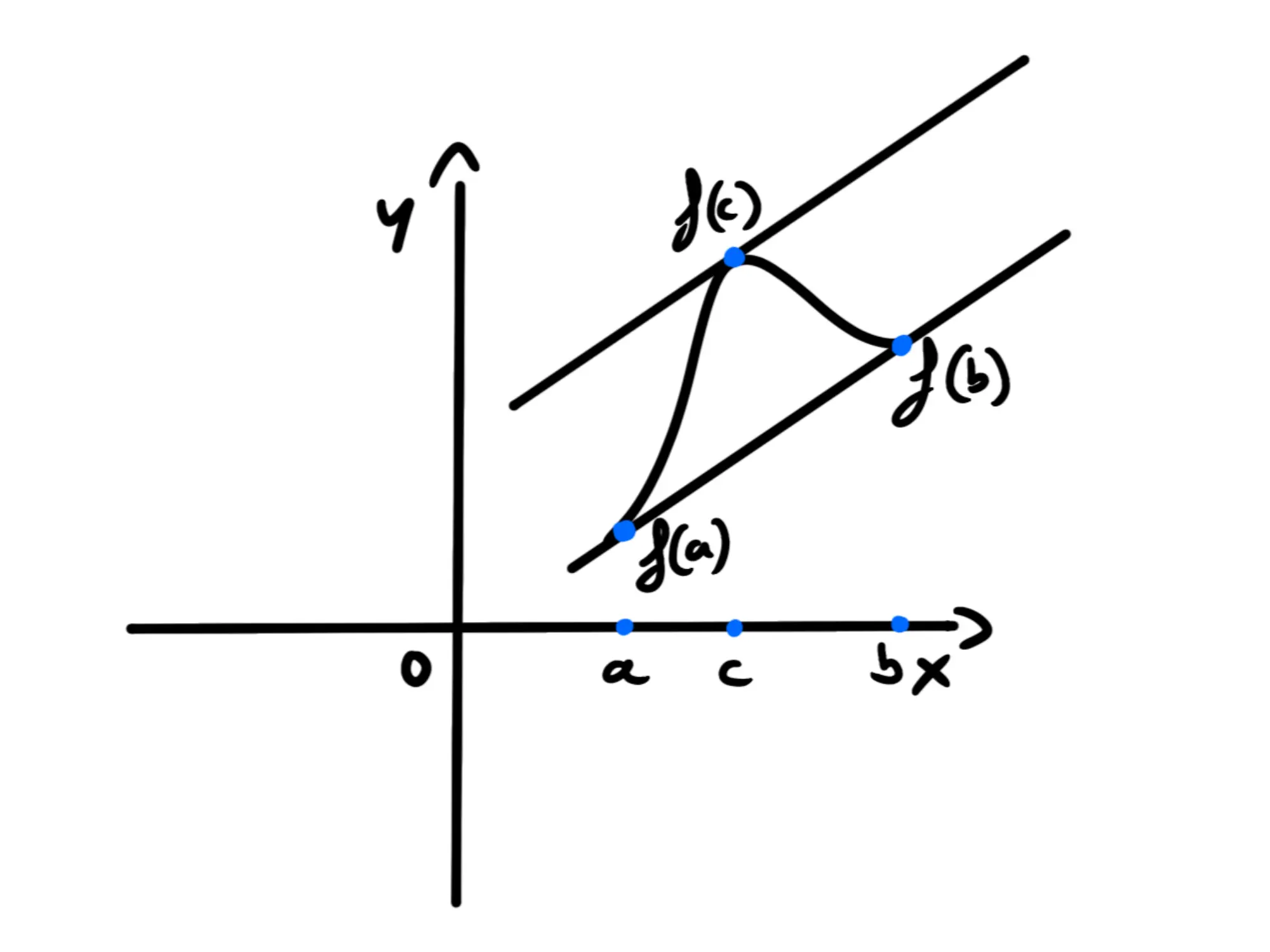
Nel caso in cui $\displaystyle { f(a)=f(b), }$ riotteniamo il teorema di Rolle, per questo si tratta di una sua generalizzazione.

Dimostriamo ora questo teorema:

Definiamo la seguente funzione:

$\displaystyle { g(x) = f(x) - kx }$

Siccome sia $\displaystyle { f(x) }$ che $\displaystyle { kx }$ sono due funzioni continue e derivabili, anche $\displaystyle { g(x) }$ lo dovrà essere.

Ora, a cosa ci serve questa nuova funzione? e quanto vale $\displaystyle { k? }$

Questa funzione sarà molto utile perché sceglieremo un $\displaystyle { k }$ tale che:

$\displaystyle { k= {f(b)-f(a)\over b-a} }$

Se andiamo ad espandere otteniamo:

$\displaystyle { (b-a)k = f(b) - f(a) }$

$\displaystyle { f(a) - ka = f(b) - kb }$

Sostituendo con $\displaystyle { g(x) }$ otteniamo:

$\displaystyle { g(a)=g(b) }$

Cioè, la funzione $\displaystyle { g(x) }$ soddisfa le condizioni per poter applicare il teorema di Rolle. Questo, quindi, è stato possibile perché potevamo scegliere qualsiasi numero reale per $\displaystyle { k. }$

Notate che $\displaystyle { a }$ e $\displaystyle { b }$ sono i due estremi di un intervallo chiuso e limitato, dunque non possono essere uguali, quindi $\displaystyle { b-a }$ deve essere diverso da $\displaystyle { 0 }$ e non ci sono quindi problemi di esistenza.

Ora sostituiamo $\displaystyle { k }$ nell'equazione per $\displaystyle { g(x): }$

$\displaystyle { g(x) = f(x) - kx }$

$\displaystyle { g(x) = f(x) - {f(b)-f(a)\over b-a}x }$

e prendiamo la derivata da entrambi i lati:

$\displaystyle { g'(x) = f'(x) - {f(b)-f(a)\over b-a} }$

Ora, però, siccome $\displaystyle { g(x) }$ soddisfava le condizioni per poter applicare il teorema di Rolle, deve esserci un punto $\displaystyle { c }$ tale che $\displaystyle { g'(c) = 0. }$ Quindi otteniamo:

$\displaystyle { g'(c) = f'(c) - {f(b)-f(a)\over b-a} }$

$\displaystyle { 0= f'(c) - {f(b)-f(a)\over b-a} }$

$\displaystyle { f'(c) = {f(b)-f(a)\over b-a} }$

Ed ecco dimostrato il teorema di Lagrange.