Dopo aver definito i tre famosi principi della termodinamica (vedili qui 👈), gli scienziati si sono resi conto dell'esistenza di un principio ancora più basilare.
Essendo il primo posto già occupato, lo chiamarono principio zero della termodinamica per indicare che stava prima del primo.
Questo principio ci interessa in questa lezione perché ci permette di definire la temperatura , infatti esso enuncia che:
Se un corpo A è in equilibrio termico con un corpo C e anche un altro corpo B è in equilibrio termico con C, allora A e B sono in equilibrio termico tra loro.
Questi tre corpi dovranno avere una grandezza fisica uguale per tutti, che chiamiamo temperatura.
Quindi se prendiamo due corpi con la stessa temperatura e li mettiamo a contatto, non succede niente sia a livello macroscopico che a livello microscopico (mentre se non lo fossero ci sarebbero scambi di calore).
Come vedremo meglio in seguito, questa temperatura esprime il livello di agitazione delle molecole del corpo.
Lo strumento di misura della temperatura è il termometro. Molti modelli sfruttano proprio il principio zero della termodinamica: mettendolo a contatto con il corpo, man mano che si raggiunge l'equilibrio termico, il termometro raggiunge la stessa temperatura del corpo in questione e sfrutta la dilatazione termica di alcuni materiali, come il mercurio, per misurarla.
Sull'unità di misura bisogna però fare un discorso a parte:
Esistono ben tre diverse unità di misura (e quindi tre diverse scale termometriche): il grado Celsius , il grado Fahrenheit e il Kelvin.
La scala Celsius è quella che utilizziamo nella vita quotidiana. A l'acqua congela e a l'acqua bolle.
La scala Fahrenheit è invece quella usata dagli americani che, per qualche strana ragione, si ostinano a non voler utilizzare le unità di misura usate nel resto del mondo. A l'acqua congela e a l'acqua bolle. Quindi ci sono di differenza tra quando l'acqua congela e quando bolle.
La scala Kelvin è invece quella usata dagli scienziati perché è quella più comoda nelle formule fisiche. è la minima temperatura possibile, detta anche zero assoluto e corrisponde a Di conseguenza, l'acqua congela a e bolle a
Iniziamo dalla conversione più semplice, cioè da Celsius a Kelvin.
In questo caso, per come sono stati definiti i gradi Kelvin, per ottenere la temperatura in Celsius basta aggiungere alla temperatura in Kelvin e cambiare le unità di misura:
Per passare da Celsius a Kelvin basta utilizzare la formula inversa:
Per passare da Fahrehneit a Celsius è un po' più complicato:
Disegniamo un grafico dove mettiamo sull'asse delle ascisse la temperatura in Celsius e sull'asse delle ordinate la temperatura in Fahrenheit:
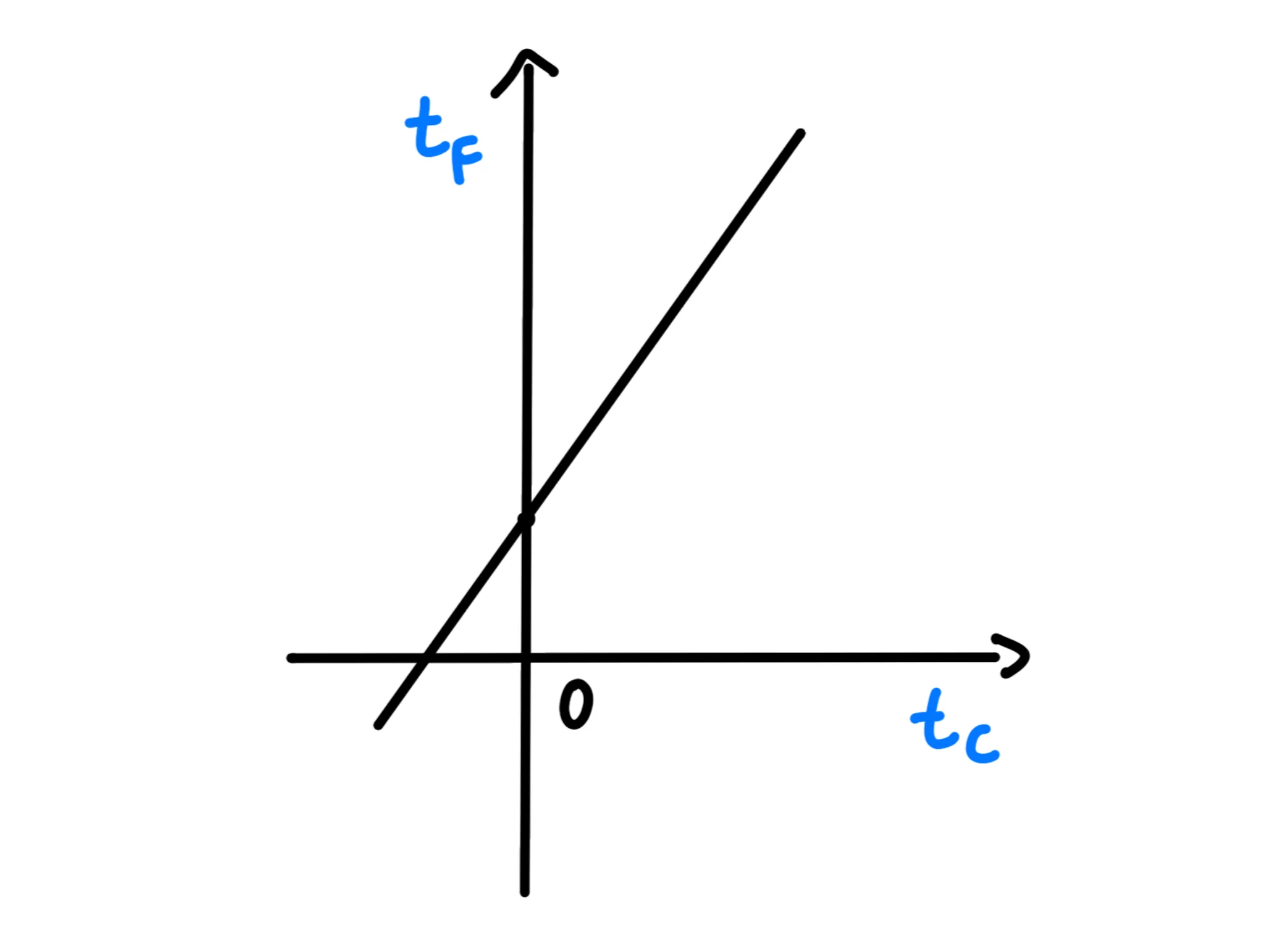
Per trovare la formula di conversione ci basta trovare l'equazione della retta. Siccome sappiamo le temperature di congelamento ed ebollizione dell'acqua in entrambe le scale, conosciamo due punti della retta.
Infatti devono essere uguali a perché ad entrambi l'acqua congela.
Allo stesso modo devono essere uguali a perché entrambi segnano quando l'acqua bolle.
Quindi la retta deve passare per i due punti e
Possiamo usare la formula della retta passante per due punti per trovare la formula di conversione:
In questo modo sapendo la temperatura in Celsius possiamo trovare quella in Fahrenheit. Per fare il contrario basta usare la formula inversa:
Infine, per poter convertire da Kelvin a Fahrenheit, basta combinare insieme le formule di conversione da Kelvin a Celsius e da Celsius a Fahrenheit:
Per convertire da Fahrenheit a Kelvin basta usare la formula inversa: