La radice quadrata di un numero è quel numero positivo che elevato al quadrato mi dà il numero iniziale.
Ad esempio, la radice quadrata di è perché al quadrato fa
Mentre la radice quadrata di fa perché al quadrato fa
Come si scrive? Dobbiamo mettere il numero di cui vogliamo fare la radice quadrata sotto questo simbolo qua:
Quindi avremo:
Ok, però quanto vale invece Potete cercare quanto volete, ma non troverete mai un numero naturale o una frazione che elevata al quadrato fa
Infatti, le radici quadrate di numeri naturali che non sono quadrati perfetti (cioè quadrati di un altro numero naturale) sono numeri irrazionali, cioè non possono essere scritti come frazioni ed hanno infinite cifre dopo la virgola.
C'è un'enorme differenze tra un numero con infinite cifre dopo la virgola come e Il primo, infatti, ha sì infinite cifre dopo la virgola, ma si ripetono seguendo un preciso schema.
Mentre è un numero decimale con infinite cifre dopo la virgola non periodico, cioè le cifre non si ripetono secondo un preciso schema.
Se uno deve fare dei conti con può approssimarla a circa
Pensate che la scoperta dell'irrazionalità della radice di fu una notizia incredibile a quel tempo.
I Pitagorici, una setta capitanata da Pitagora (quello del teorema), avevano fondato la loro filosofia sull'armonia e il rapporto tra i numeri. Secondo loro tutto poteva essere espresso tramite una frazione.
Quando Ippasio di Metaponto, dunque, dimostrò che la radice di due era irrazionale, il loro potere si sgretolò e Pitagora fu costretto a scappare e morì nella fuga perché finì dentro un campo di fave di cui era allergico.
Ok, chiusa questa parentesi di storia della matematica, torniamo al come si calcolano le radici quadrate. Come trovare, ad esempio, quanto vale
Esiste un algoritmo, cioè una serie di passaggi da svolgere, che ci permette di trovare il suo valore esatto se il numero è un quadrato perfetto, sennò ci fa trovare la sua parte intera e le prime cifre dopo la virgola.
Iniziamo scrivendo il nostro numero sul foglio:

Ora disegniamo il simbolo della radice quadrata sopra il numero e dall'estremo destro facciamo partire una riga verso il basso:

Adesso, partendo da destra, mettiamo un punto ogni due numeri. In questo modo suddivideremo il numero in blocchetti da due tranne l'ultimo che potrà essere da uno se il numero delle cifre è dispari (come nel nostro caso):

Adesso dobbiamo partire dal blocchetto più a sinistra, quindi da Dobbiamo chiederci: "qual'è il quadrato più piccolo che non supera " Si tratta di (perché quello successivo è che è troppo grande).
Quindi scriviamo il sotto il e mettiamo la radice quadrata di che sarebbe a destra della riga alla stessa altezza del su di un segmento orizzontale:

Sottraiamo a ottenendo ed abbassiamo il prossimo blocco:
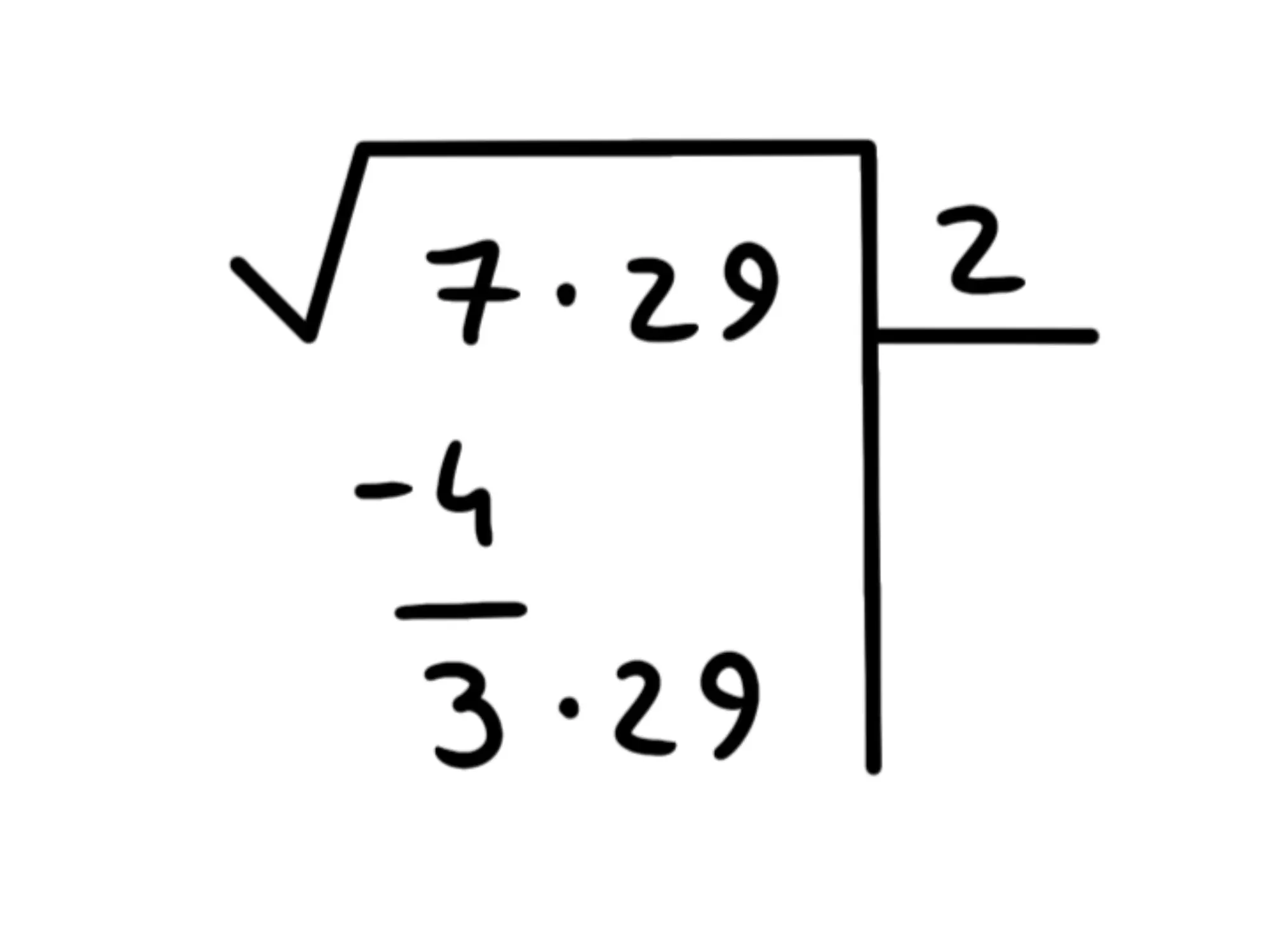
Adesso dobbiamo prendere il numero che sta in alto a destra, cioè il e raddoppiarlo.
Attenti a non dimenticarvi di questo passaggio.
Otteniamo quindi Ora aggiungiamo una cifra a e moltiplichiamo quello che otteniamo per la stessa cifra. Ad esempio, se scelgo come cifra, dovrò fare
Come scelgo la mia cifra? Devo trovare, andando a tentativi, quella che mi fa venire il risultato più vicino a senza però che lo superi. Se quindi mi esce come il risultato della moltiplicazione, non va bene e dovrò prendere la cifra precedente.
Quindi, proviamo con il Facciamo i conti sotto alla riga orizzontale:
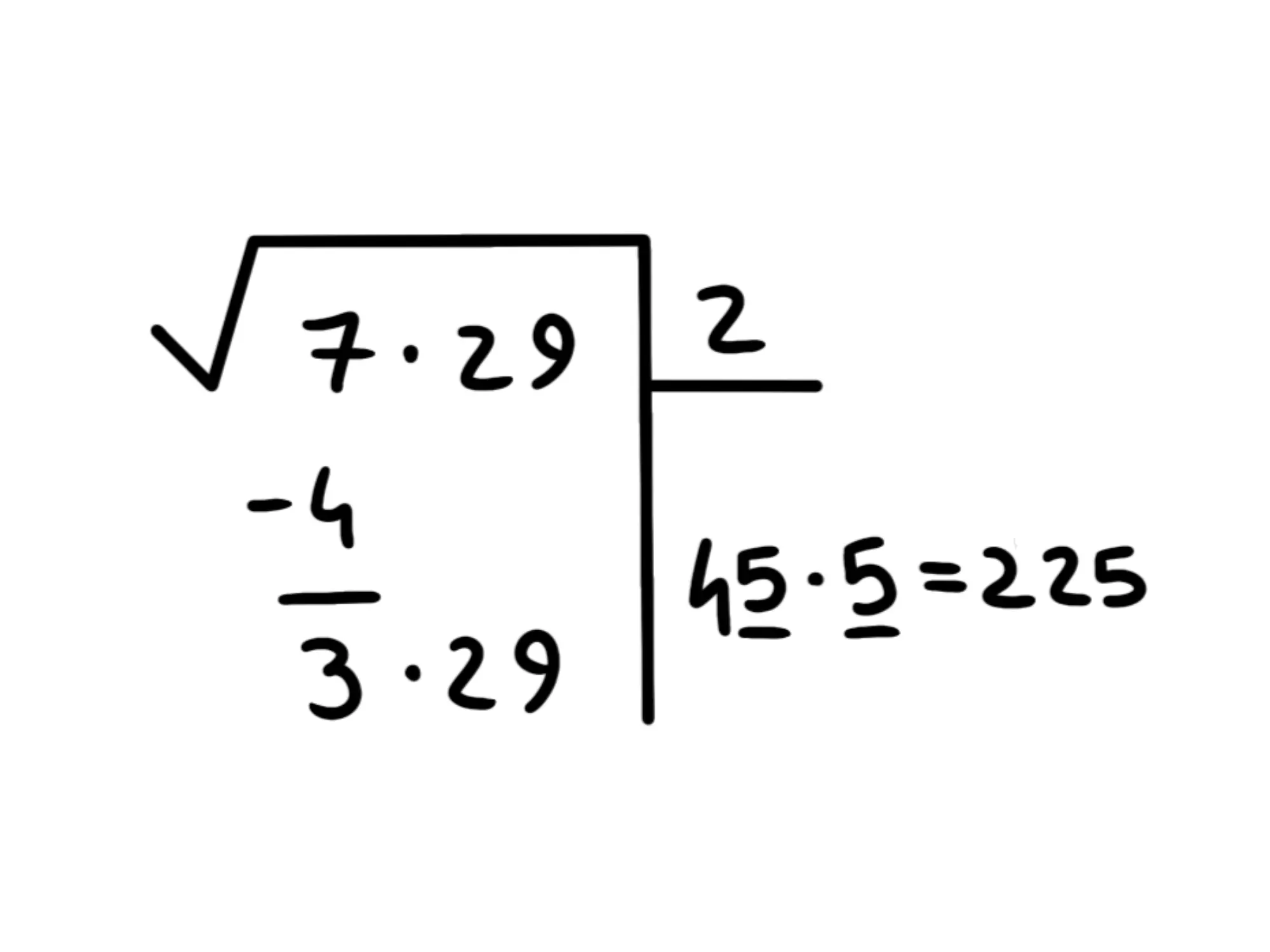
Ok, ci esce che è meno di Proviamo quindi col
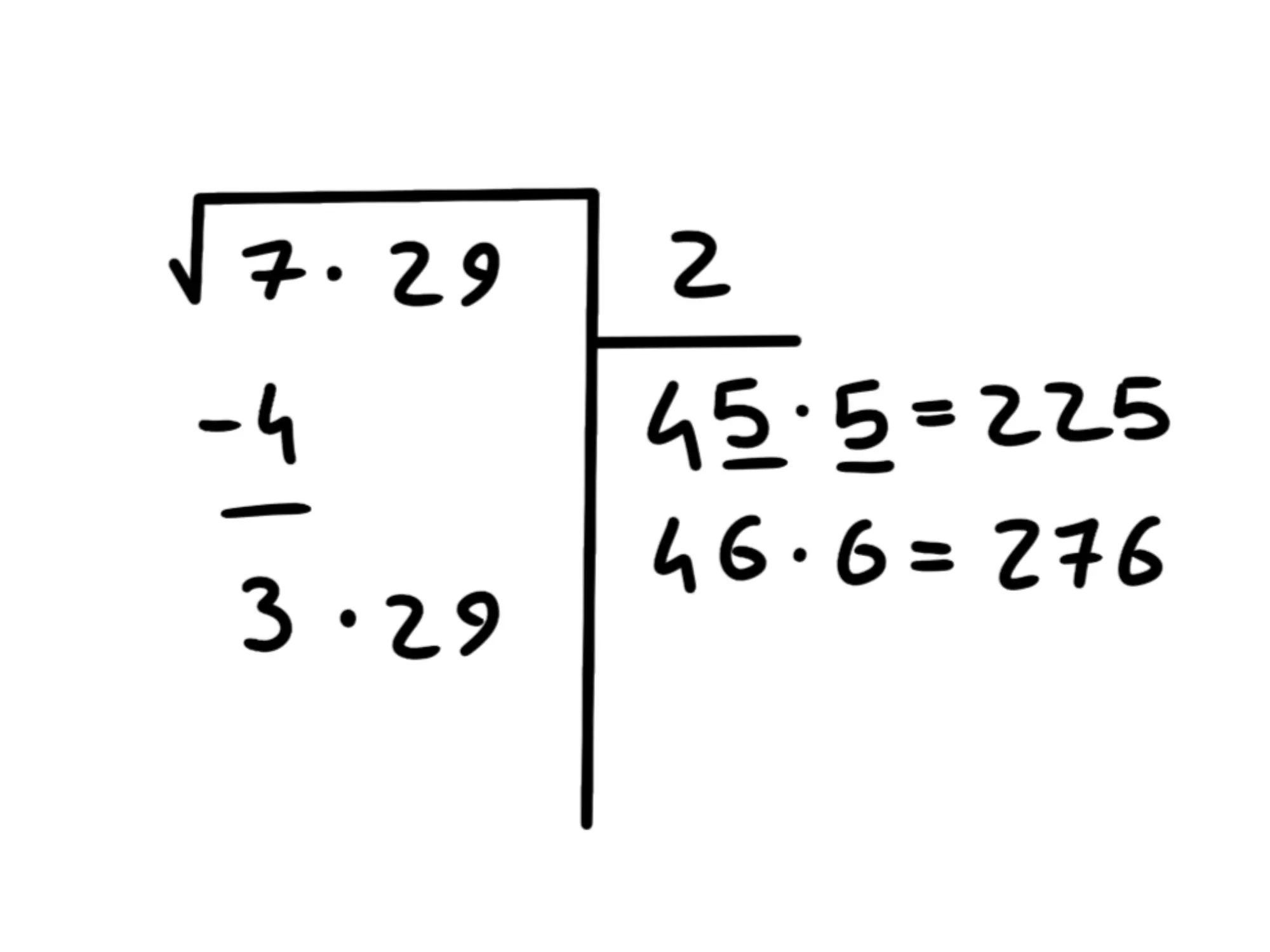
Ci esce che è ancora minore di quindi proviamo col
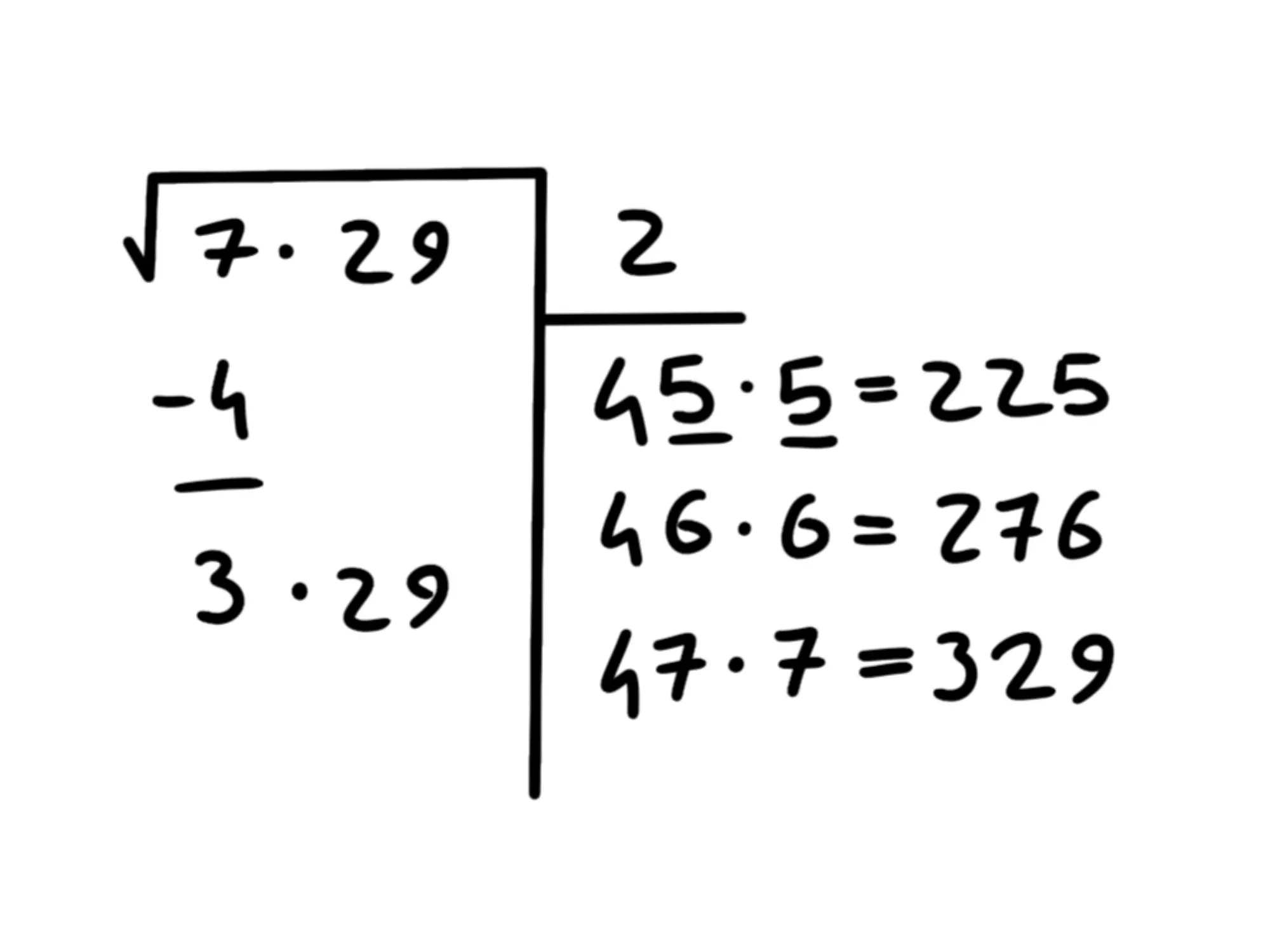
Ci esce esattamente Vuol dire che la cifra giusta è che dunque scriviamo sopra, accanto al Sottraiamo ed otteniamo
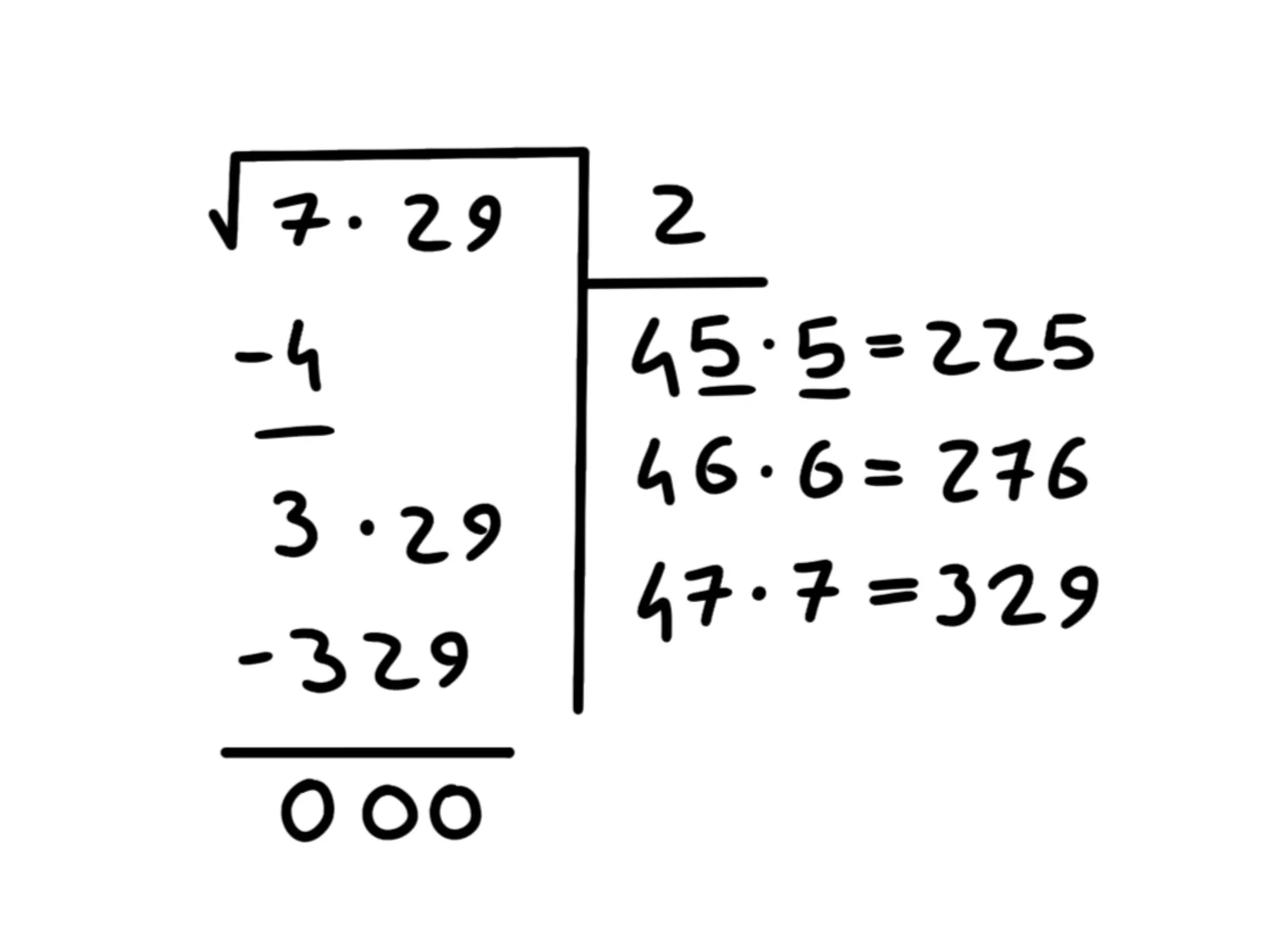
Ci è uscito quindi vuol dire che abbiamo finito è che il risultato è Infatti
Ok, però ci è uscito perché era un quadrato perfetto, ma come faccio a calcolare la radice quadrata di un numero che non è un quadrato perfetto, come ad esempio
In tal caso, siccome la sua radice avrà infinite cifre dopo la virgola, non possiamo trovare quanto vale esattamente, ma possiamo trovare le sue prime cifre decimali, in modo da ottenere una buona approssimazione.
La parte iniziale è la stessa: scriviamo il numero, facciamo lo schema e dividiamo il numero in blocchi da due partendo da destra:
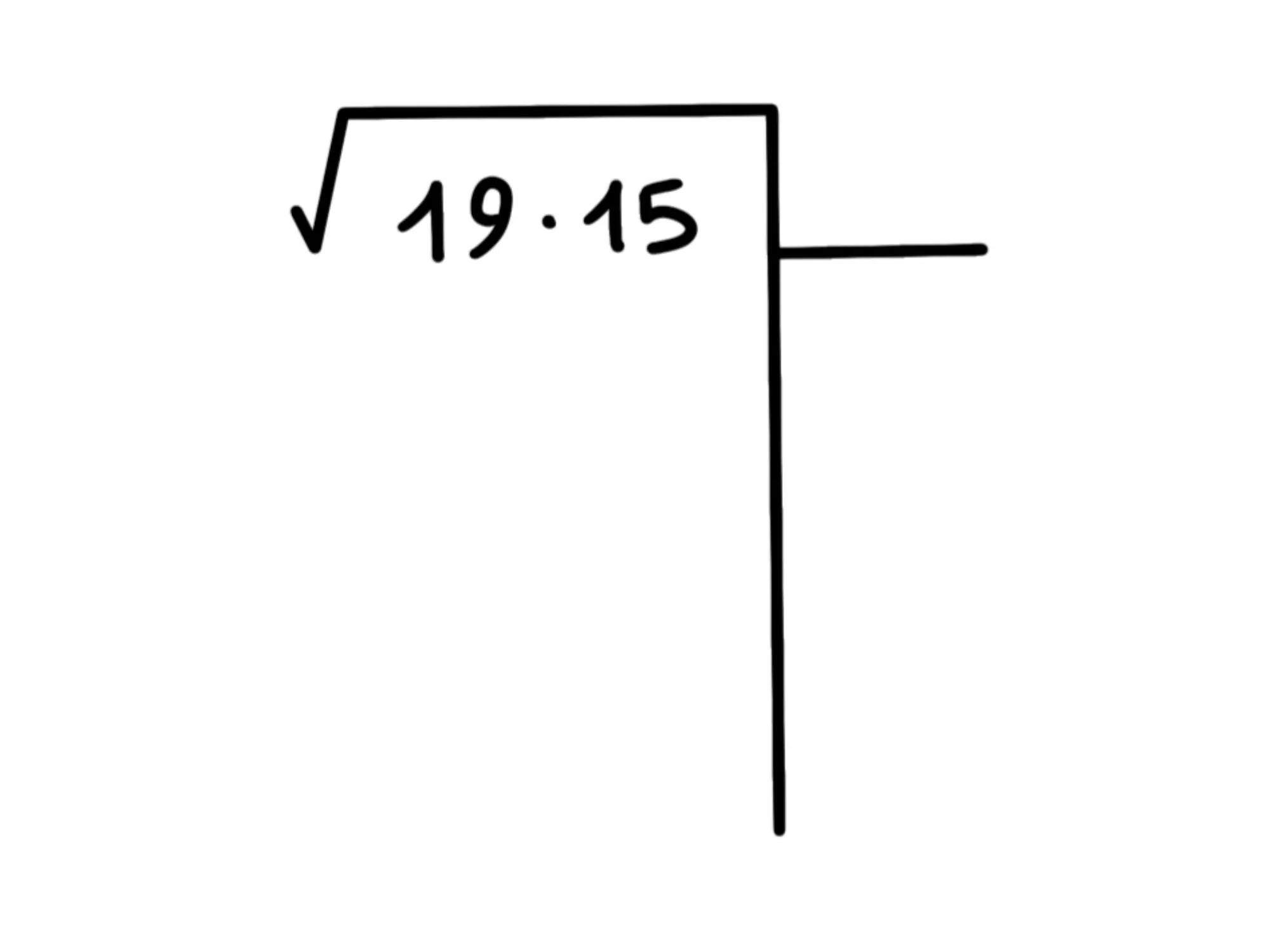
Qual'è il quadrato più grande che non supera E' Quindi sottraiamo e scriviamo in alto a destra:
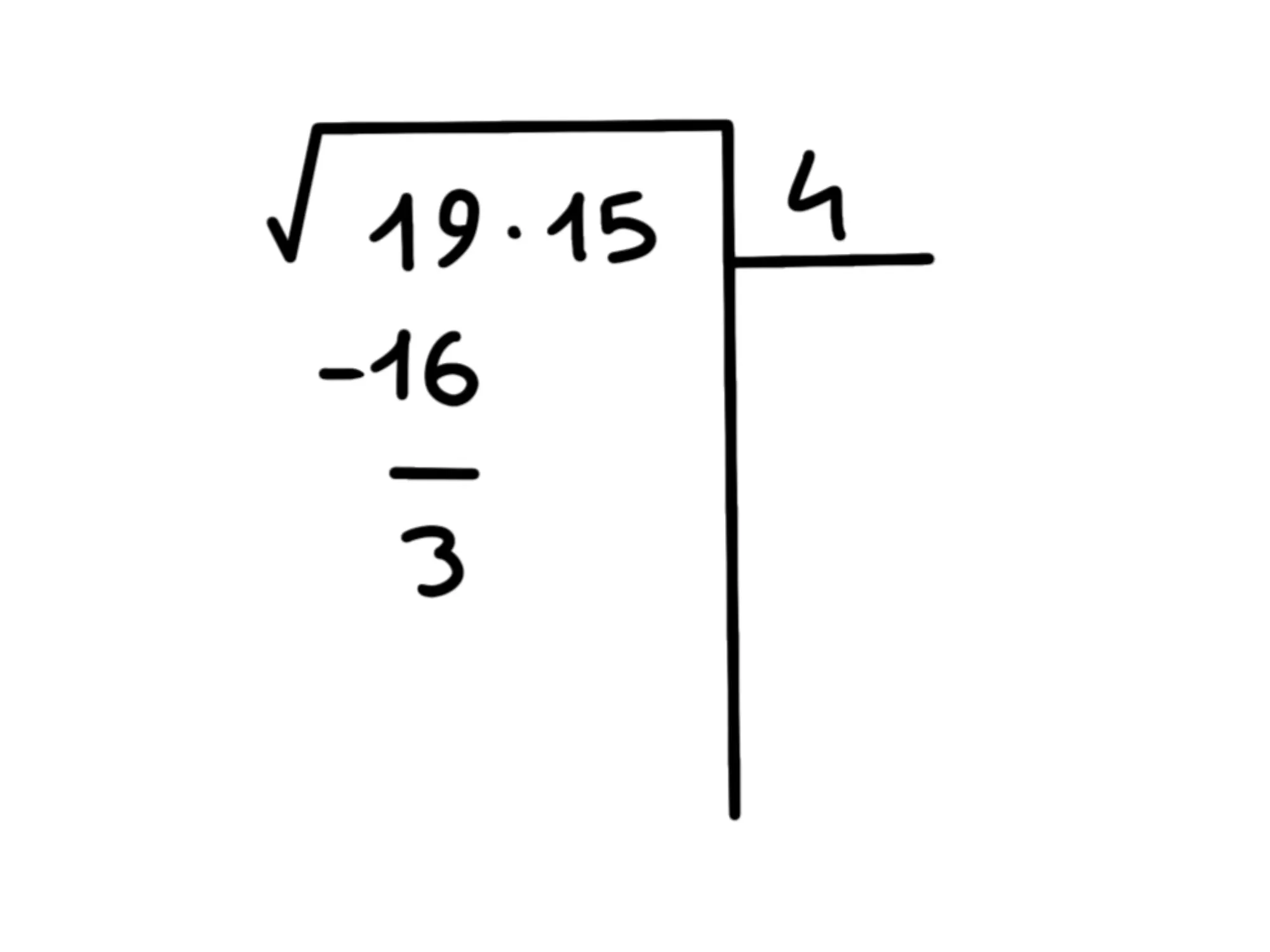
Ora portiamo giù il prossimo blocco:

Raddoppiamo il ottenendo e cerchiamo la cifra da aggiungergli e per la quale moltiplicare. Proviamo con il
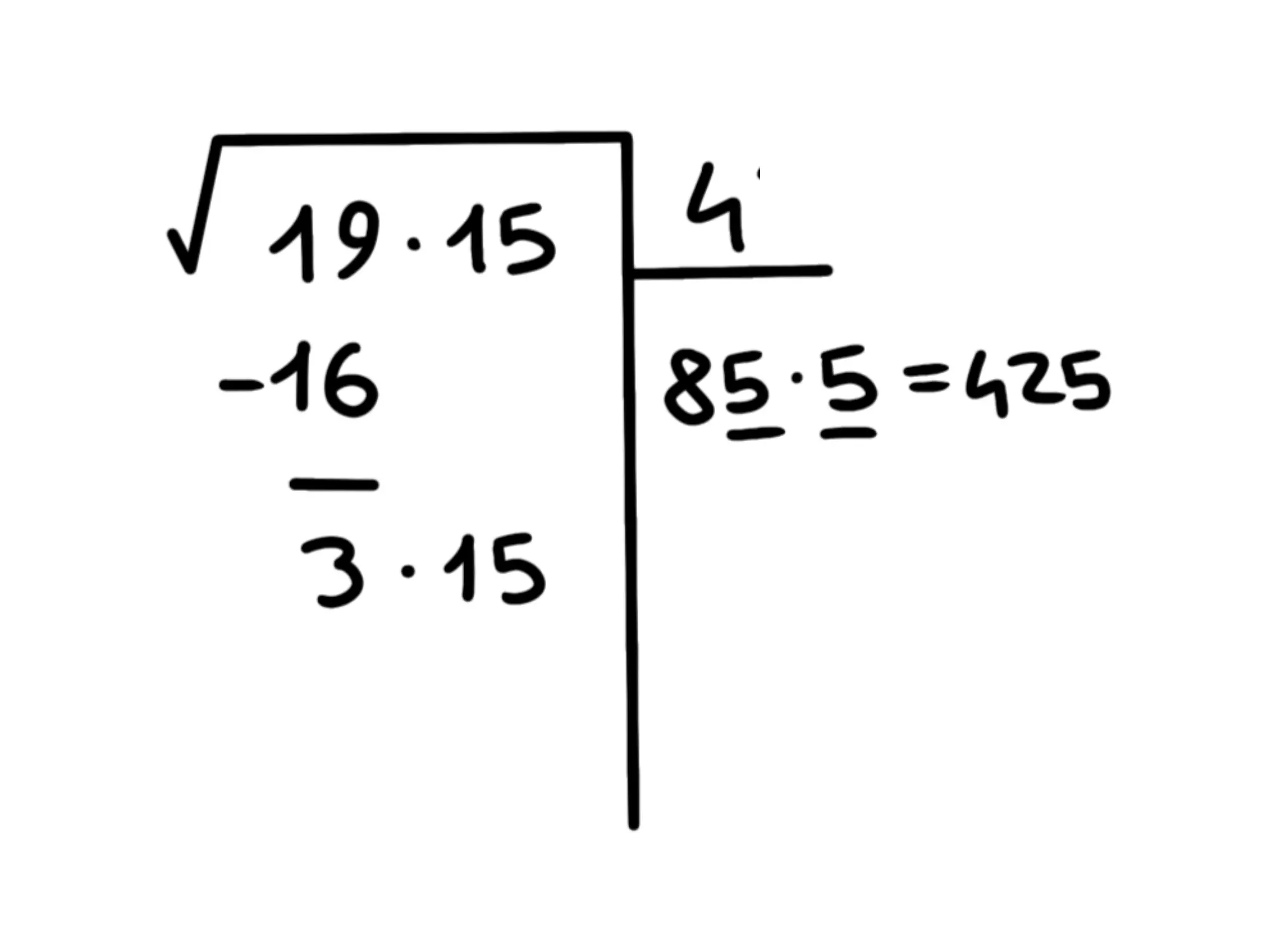
Esce non va bene perché supera Proviamo con il
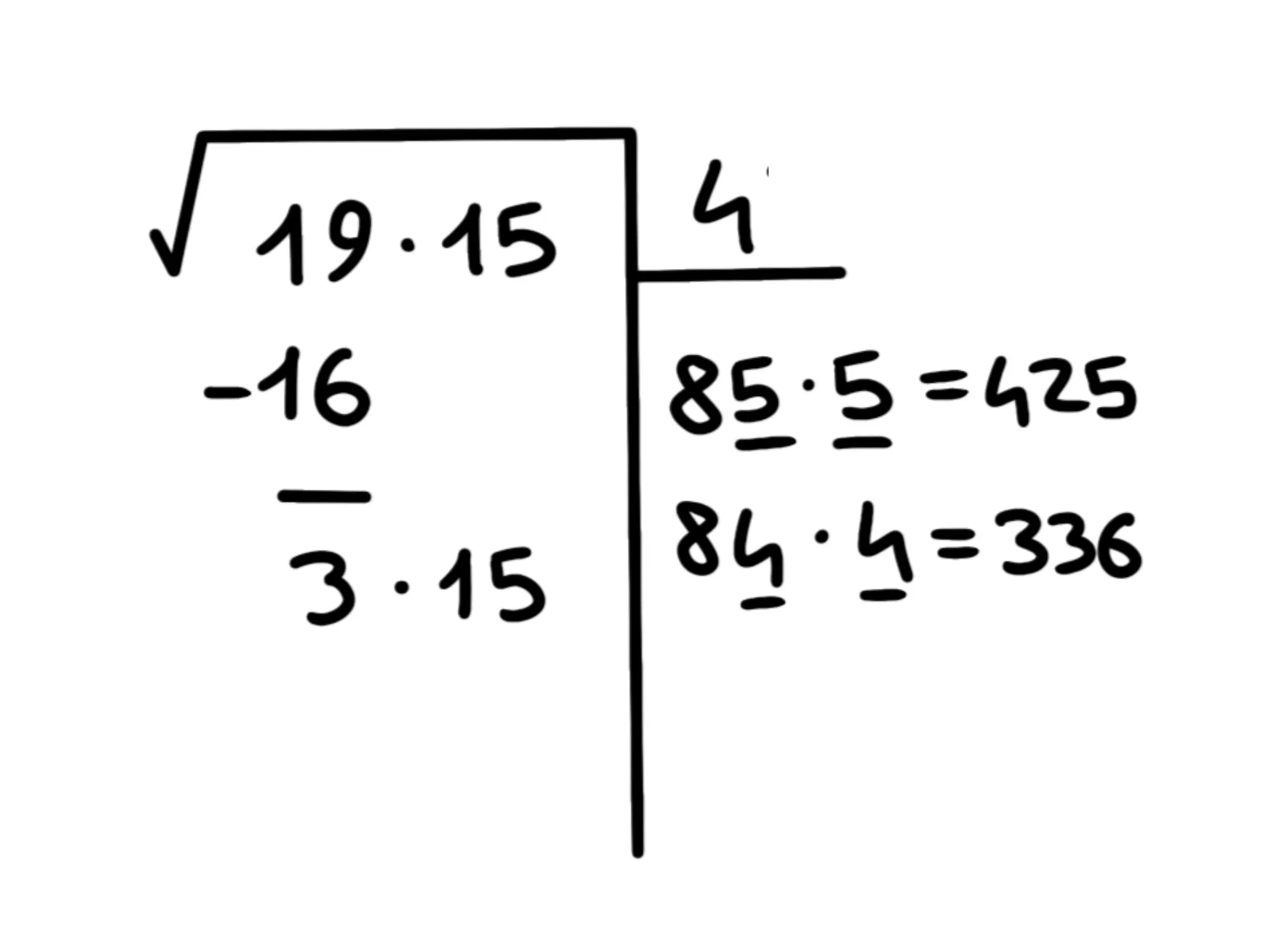
Esce è ancora troppo grande quindi proviamo con il
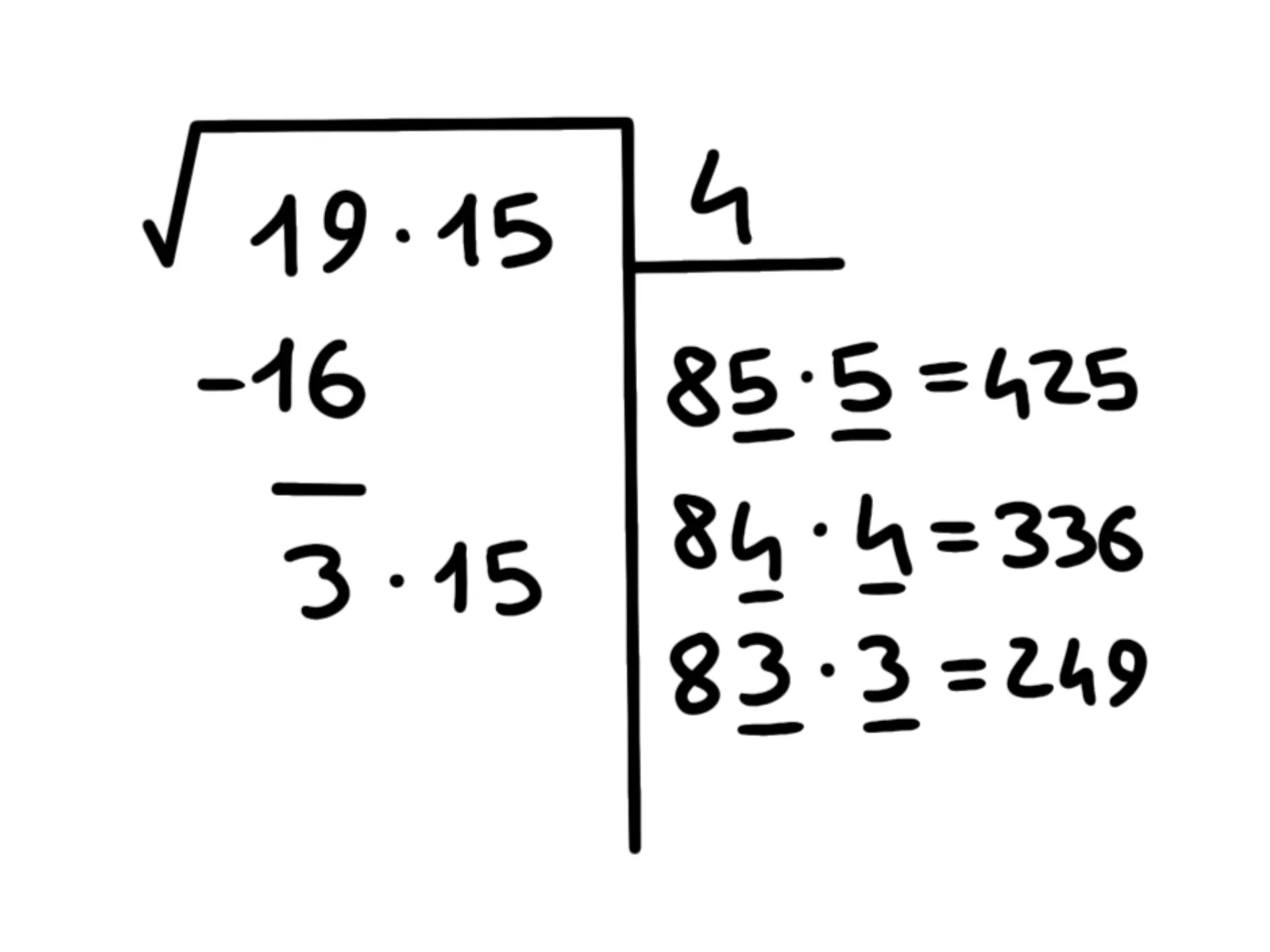
Ok, viene che è minore di La cifra che cerchiamo sarà dunque perché è il massimo che possiamo mettere prima di superare
Ora sottraiamo e mettiamo il in alto dopo il
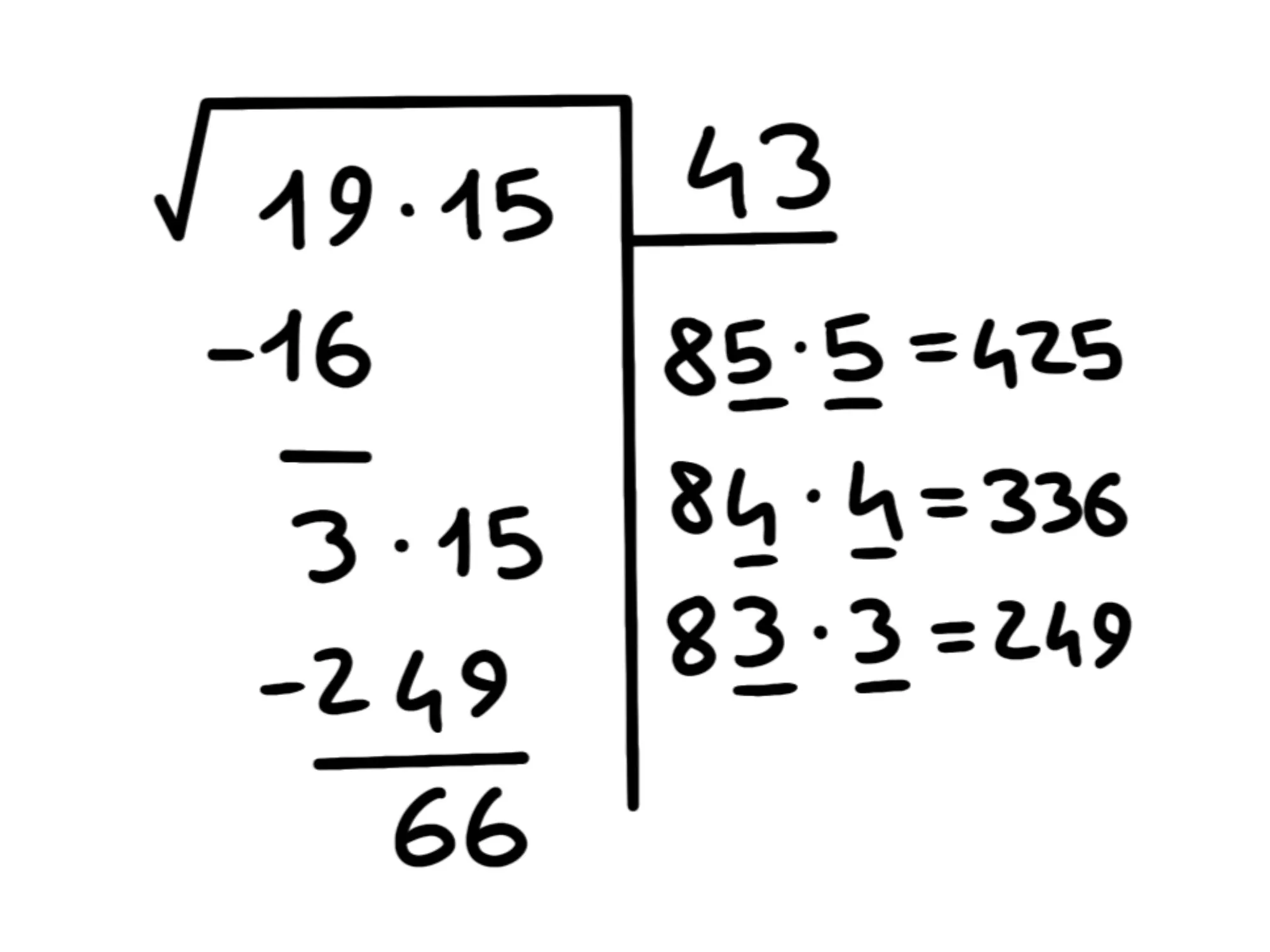
Non ci è uscito quindi, come avevamo anticipato prima, non è un quadrato perfetto e la sua radice avrà infinite cifre dopo la virgola. Cerchiamo le prime due cifre.
Per farlo, dobbiamo riscrivere come come
Cioè dobbiamo aggiungere due zeri dopo la virgola per ogni cifra che vogliamo trovare:
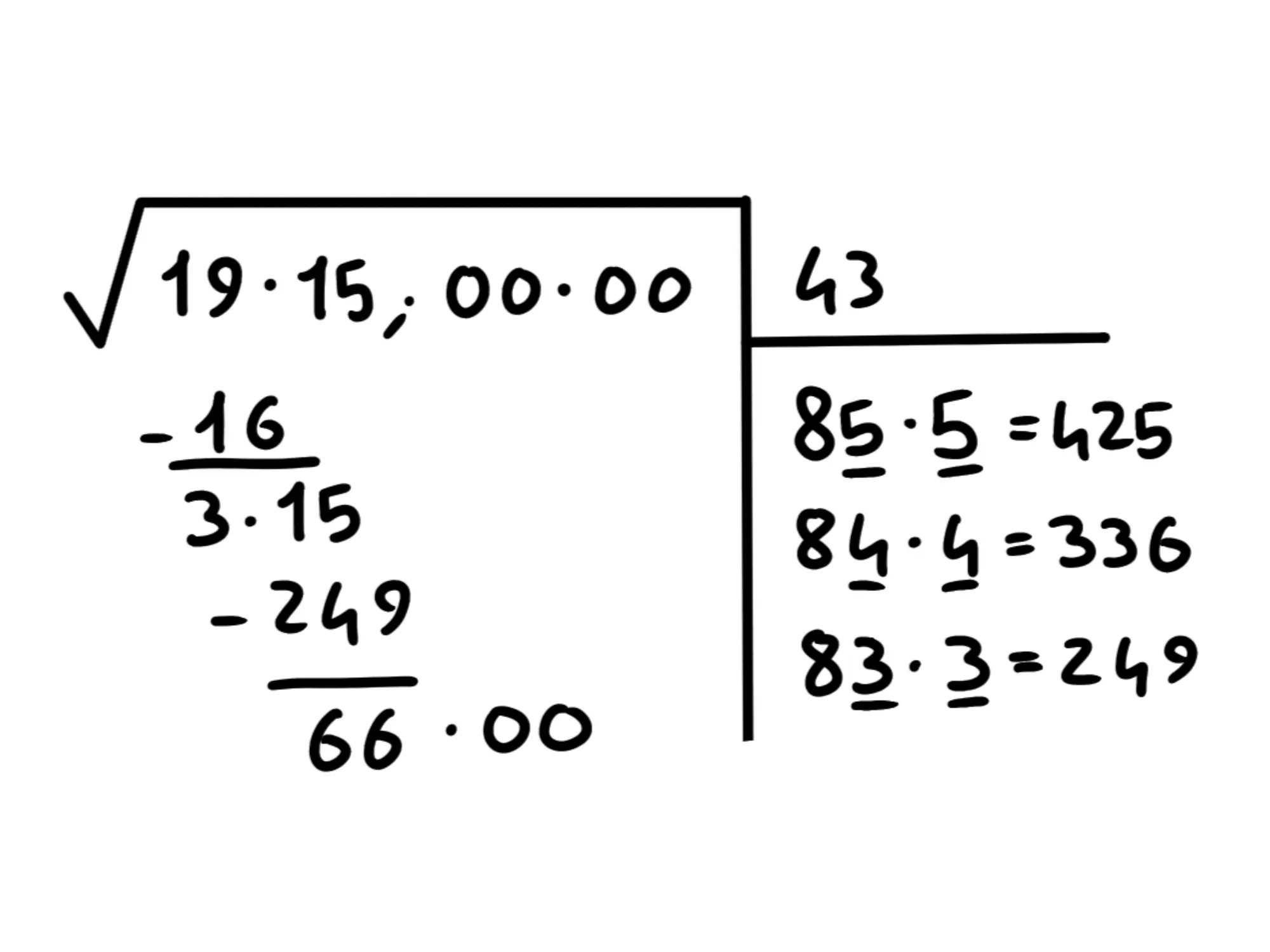
Adesso mettiamo la virgola dopo il e continuiamo con l'algoritmo. Abbassiamo il prossimo blocco:
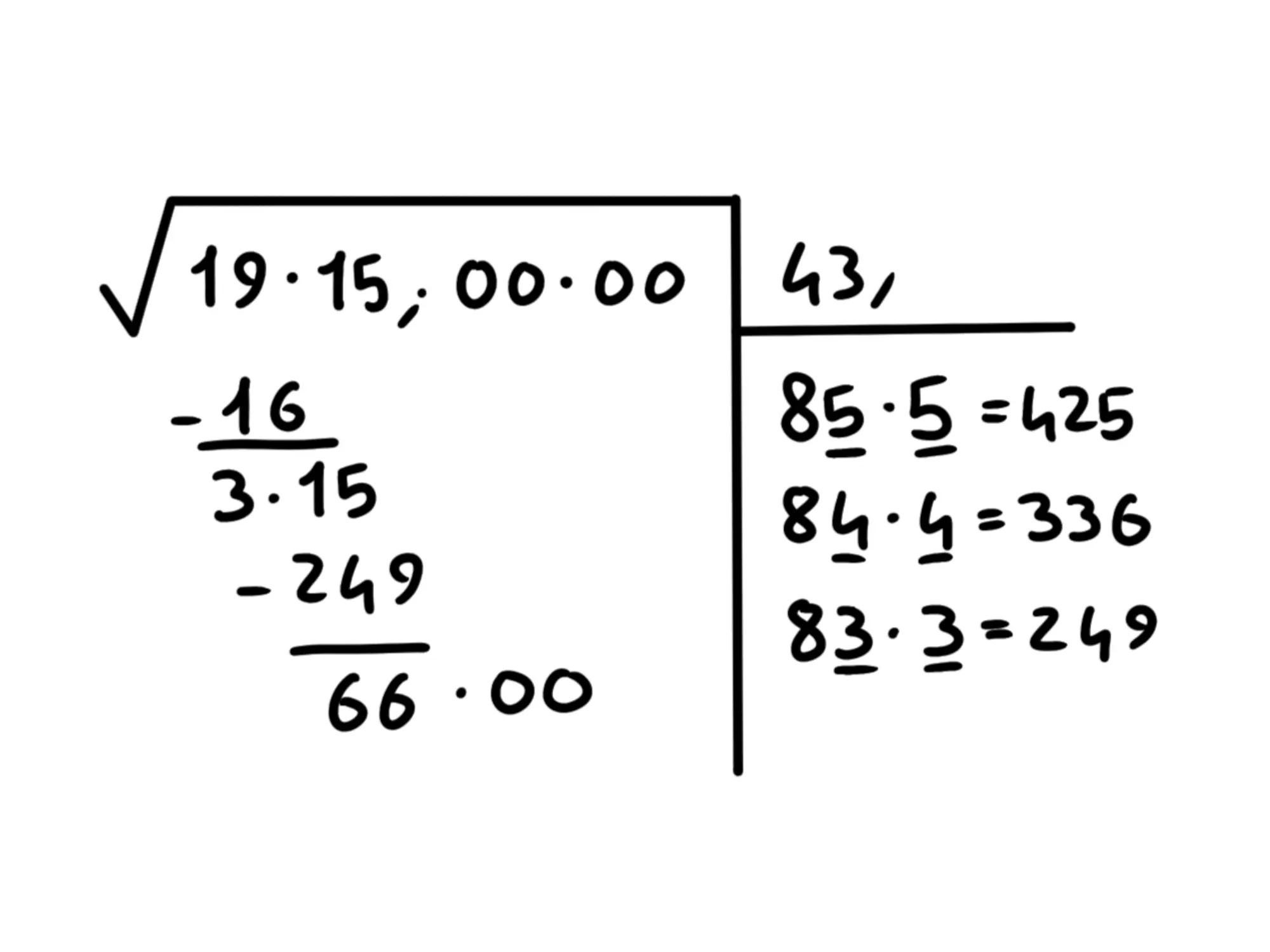
Ora raddoppiamo il ottenendo e cerchiamo quale cifra dobbiamo usare per avvicinarci il più possibile a senza però superarlo.
Facendo un po' di tentativi scopriamo che è con la quale otteniamo Applichiamo dunque i soliti step e scriviamo dopo la virgola:
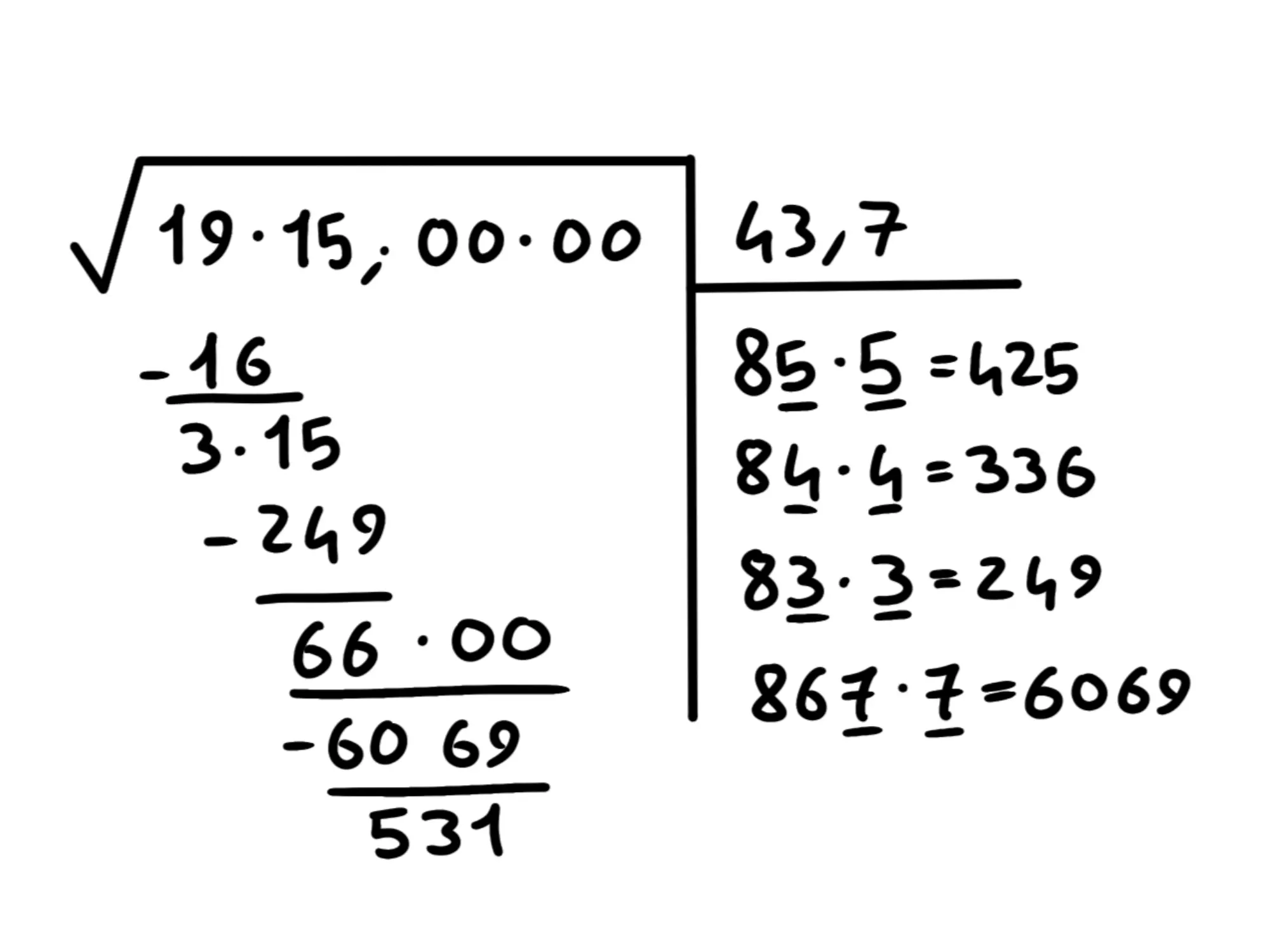
Adesso, quando raddoppiamo dobbiamo togliergli la virgola. Perciò dobbiamo usare Facendo dei tentativi otteniamo che la cifra che ci serve è per la quale otteniamo Applichiamo un'ultima volta gli step per ottenere:

Abbiamo dunque ottenuto che la radice quadrata di vale circa Se vogliamo cercare altre cifre dopo la virgola, ci basta aggiungere altri blocchi da due zeri e continuare il processo.