I punti notevoli dei triangoli sono una serie di punti ottenuti dall'intersezione di alcuni segmenti particolari. Essi sono il baricentro, l'ortocentro, l'incentro, il circocentro e l'excentro .
Questi punti possiedono delle informazioni importanti ed alcune proprietà utili.
Studiamoli uno ad uno:
Il baricentro di un triangolo è il punto di incrocio delle sue mediane:
Ricordiamo che la mediana di un lato è il segmento che congiunge il punto medio del lato al vertice opposto.

Il baricentro si trova sempre all'interno del triangolo e divide le mediane in due parti.
Quella che parte dal vertice è sempre lunga il doppio di quella che arriva alla base:

Avrete sentito parlare del baricentro in fisica quando studiavate l'equilibrio delle forze e si tratta dello stesso baricentro, non è una coincidenza.
L'ortocentro di un triangolo è il punto di incontro delle sue altezze:
Ricordiamo che l'altezza di un lato è il segmento perpendicolare al lato che lo congiunge al suo vertice opposto. (può anche cadere su un prolungamento del lato)

Al contrario del baricentro, l'ortocentro può trovarsi dentro o fuori del triangolo. La sua posizione ci da informazioni importanti sul triangolo in questione:
Se l'ortocentro si trova all'esterno del triangolo, allora il triangolo deve essere ottusangolo (cioè ha un angolo ottuso, ovvero maggiore di ):

Se invece l'ortocentro si trova all'interno del triangolo, allora il triangolo deve essere acutangolo (cioè non ha angoli superiori a ):

Se, infine, l'ortocentro si trova su un vertice del triangolo, allora il triangolo deve essere retto in quel vertice:

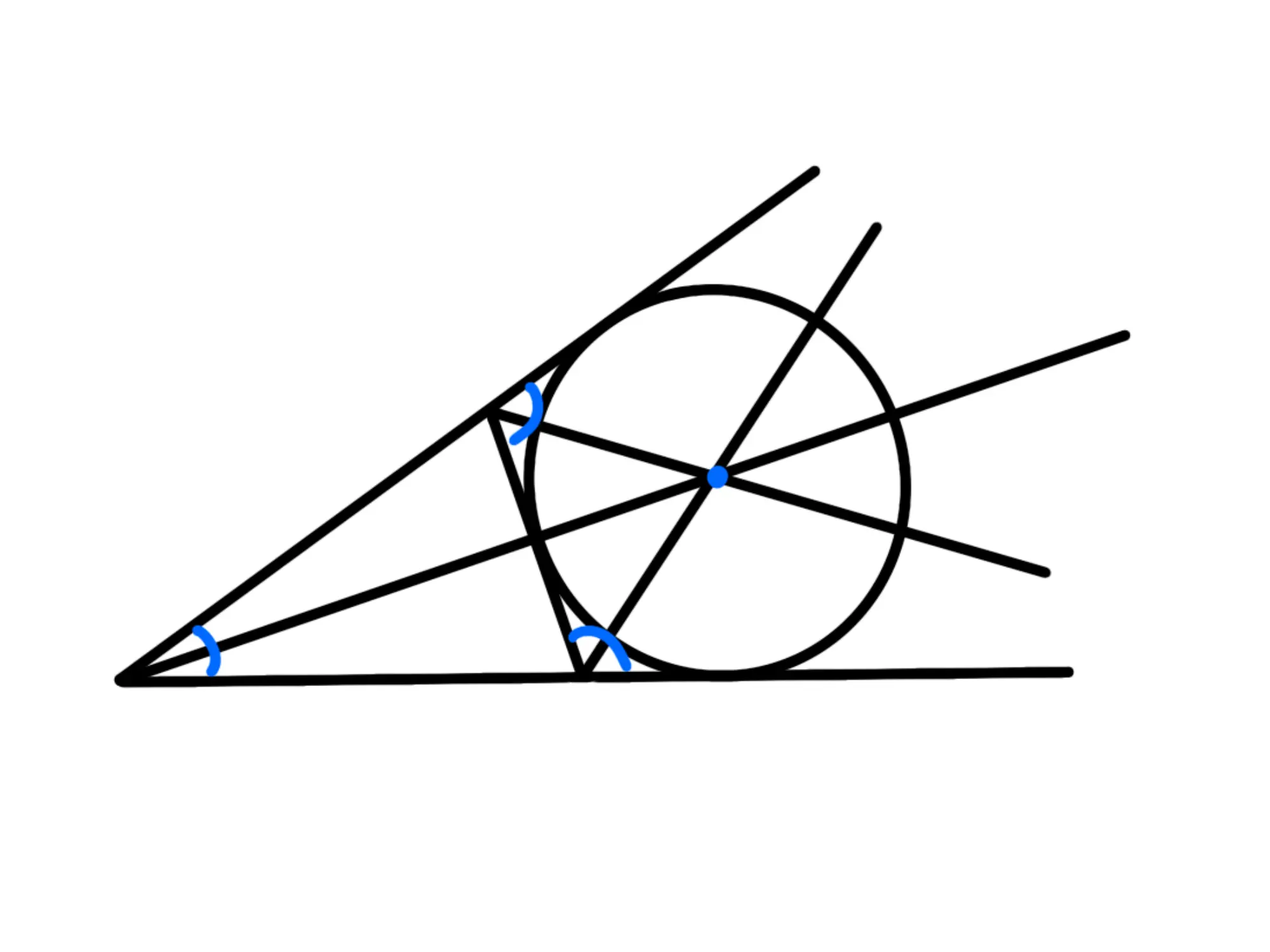
L'incentro di un triangolo è il punto di incontro delle sue bisettrici:
Ricordiamo che la bisettrice di un angolo è il segmento che parte dal vertice e divide l'angolo in due angoli congruenti.

L'incentro è il centro della circonferenza iscritta nel triangolo:

Infatti l'incentro dista ugualmente da tutti e tre i lati e si trova sempre all'interno del triangolo.
Inoltre, se prendiamo il seguente triangolo:

Dobbiamo avere:
Il circocentro di un triangolo è il punto di incontro degli assi dei suoi segmenti:

Ricordiamo che l'asse di un segmento è la retta che passa perpendicolarmente nel punto medio del segmento.
Il circocentro è anche il centro della circonferenza circoscritta al triangolo:

Come l'ortocentro, può trovarsi dentro o fuori del triangolo e la sua posizione ci da informazioni sul triangolo:
L' excentro è il punto di incontro delle bisettrici di due angoli esterni e della bisettrice dell'altro angolo:

Un triangolo avrà quindi excentri. Ecco gli altri due del triangolo qui sopra:


Per comprendere di quale excentro stiamo parlando, quindi, dobbiamo dire rispetto a quale lato lo stiamo prendendo.
L'excentro è anche il centro della circonferenza tangente al lato rispetto al quale l'abbiamo preso e ai prolungamenti degli altri due lati: