Piani nello spazio
In questa lezione sui piani nello spazio vedremo come trovare le loro equazioni e come possono interagire tra loro.
 Cosa devo già sapere?
Cosa devo già sapere?Equazione di un piano nello spazio
Iniziamo ricordandoci l'equazione di una retta in uno spazio 2D. Essa era della forma:
ax+by+c=0
Il suo grafico era qualcosa del seguente tipo:

Ora, vediamo invece il grafico di questa stessa equazione, ma questa volta in un spazio 3D:
Siccome la nuova variabile z non influisce sull'equazione, otterremo la stessa identica retta per tutti i valori di zeta.

Se disegnassimo una retta per ogni singolo valore di z, otterremo una serie di rette parallele una attaccata all'altra:

Se poi nell'equazione introduciamo z, al suo variare le rette si alzeranno o abbasseranno a seconda del suo coefficiente.
Se prendiamo per esempio l'equazione:
2x+3y+2z+1=0
Per z=0 otteniamo la retta:
2x+3y+1=0
mentre per z=2 otteniamo la retta:
2x+3y+5=0
Otteniamo quindi un piano "più inclinato":

E' facile convincerci che tutte le equazioni di questo tipo danno vita a un piano nello spazio, ma tutti i piani nello spazio hanno questo tipo di equazione o abbiamo preso solo un caso particolare?
Tutti i piani hanno questa tipologia di equazione ma adesso non lo dimostreremo.
Invece, vogliamo chiederci come trovare l'equazione di un piano che passa per 3 punti:
Dalla geometria euclidea sappiamo che per tre punti passa uno e soltanto un piano, dunque deve esistere un modo per trovarlo.
Dunque prendiamo tre punti P(x_p;y_p;z_p), T(x_t;y_t;z_t) e S(x_s;y_s;z_s) e l'equazione generale del piano:
ax+bx+cz+d=0
Siccome i punti appartengono al piano, possiamo sostituire le loro coordinate nell'equazione del piano ed ottenere un sistema con tre equazioni:
\left\{\begin{array}{l}ax_p+by_p+cz_p+d=0 \\ ax_t+by_t+cz_t+d=0 \\ax_s+by_s+cz_s+d=0\end{array}\right.
Dobbiamo trovare a, b, c e d, quindi abbiamo 4 incognite ma solo 3 equazioni, come facciamo?
Questa problema si era già presentato quando volevamo trovare l'equazione di una retta scritta in forma implicita conoscendo solo due punti.
Anche lì avevamo un'incognita in più di quante equazioni avessimo. Quindi, sappiamo già che in realtà le vere incognite sono solo 3. Infatti, non esiste una sola serie di coefficienti dell'equazione per un piano, ma infinite. In che senso?
Prendiamo l'equazione di un piano:
3x+2y+z+3=0
Possiamo moltiplicare entrambi i lati per 2 ed ottenere:
6x+4y+2z+6=0
I coefficienti sono tutti diversi, ma l'equazione è la stessa. Per risolvere questo problema possiamo esprimere 3 delle incognite in funzione della quarta e sostituendo potremo seplificare. Vediamo un esempio:
Cerchiamo il piano passante per i punti P(1;0;0), T(4;1;0), S(2;1;-4)
Mettendo a sistema otteniamo:
\left\{\begin{array}{l} a+d=0 \\ 4a+b+d=0 \\ 2a+b-4c+d=0 \end{array}\right.
Isoliamo quindi tutte le incognite in funzione di d:
\left\{\begin{array}{l} a=-d \\ 4a+b+d=0 \\ 2a+b-4c+d=0 \end{array}\right.
\left\{\begin{array}{l} a=-d \\ -4d+b+d=0 \\ -2d+b-4c+d=0 \end{array}\right.
\left\{\begin{array}{l} a=-d \\ b=3d \\ -2d+3d-4c+d=0 \end{array}\right.
\left\{\begin{array}{l} a=-d \\ b=3d \\ c={d\over 2} \end{array}\right.
Adesso sostituiamo all'interno dell'equazione del piano:
ax+by+cz+d=0
-dx+3dy+{d\over 2}z+d=0
Ovviamente d è diverso da 0, altrimenti non otterremo più un'equazione di un piano ma un'equazione del tipo 0=0, dunque possiamo dividere per d:
-x+3y+{1\over 2}z+1=0
Il concetto è che, appunto, siccome moltiplicare entrambi i lati dell'equazione per un qualche numero non la cambia, possiamo scrivere tutto in funzione di una delle incognite e quindi semplificare per ottenere l'equazione del piano.
Se sostituiamo i punti nell'equazione trovata, noteremo che la soddisfano, come aspettato.
Piani particolari
Fra tutti i piani, ne esistono alcuni di particolare interesse:
Se imponiamo tutti i coefficenti tranne quello della x uguali a 0, otteniamo:
ax+0y+0z+0=0
Ovvero:
ax=0
Che equivale a:
x=0
I punti che soddisfano questa condizione sono quelli sul piano y-z:

Analogamento, il piano x-y avrà equazione z=0 e il piano x-z avrà equazione y=0


Questi piani risultono molto utili in varie situazione quindi è bene conoscere le lore equazioni.
Relazioni tra piani nello spazio
Esistono tre tipi di relazioni tra piani:
La prima è che siano due piani coincidenti. Questo avviene quando tutti i punti del primo appartengono anche al secondo e viceversa.

Oppure, se i due piani non hanno alcun punto in comune, i due piani sono paralleli.

Infine, se hanno dei punti in comune, ma non tutti, si dice che sono due piani incidenti.

In particolare, se due piani sono incidenti, la loro intersezione genera una retta. Ricordatevi di questo perché lo useremo quando studieremo la retta nello spazio.
Come sapere che relazione c'è tra due piani conoscendo la loro equazione?
Per essere dei piani coincidenti, devono avere la stessa equazione. Dunque basta guardare se la seconda equazione è esattamente un multiplo della prima.
Per esempio i due piani con equazione:
x+y+3z+4=0
e
2x+2y+6z+8=0
Sono coincidenti perché moltiplicando per 2 la prima equazione otteniamo la seconda.
Per verificare in casi più difficili se la seconda è un multiplo della prima, basta guardare se i rapporti tra i corrispettivi coefficienti è uguale. Nel caso di prima, infatti, il rapporto è sempre uguale 2.
Possiamo pensare a due piani paralleli come a due piani coincidenti dove abbiamo preso uno dei due piani e l'abbiamo abbassato o alzato nello spazio per una certa costante k:

Dunque, se due piani sono paralleli, dobbiamo poter scrivere l'equazione del secondo come quella di un piano coincidente al primo a cui è stata aggiounta una costante k.
Questo vuol dire che i rapporti tra i coefficienti della x, della y e della z devono essere uguali, ma quello dei termini noti deve essere diverso. Vediamo un esempio:
Prendiamo i due piani di equazione:
2x+3y+z+1=0
e
6x+9y+3x+10=0
Il rapporto tra i coefficienti delle x è uguale a 6\over 2, ovvero a 3.
Il rapporto tra i coefficenti delle y è uguale a 9\over 3, ovvero a 3.
Anche il rapporto tra i coefficenti delle z, essendo pari a 3\over 1, è uguale a 3.
Però, il rapporto tra i coefficenti dei termini noti è pari a 10\over 1, ovvero a 10, che ovviamente è diverso da 3.
Dunque i due piani sono paralleli.
Infine, se i due piani non sono né coincidenti né paralleli, devono essere incidenti.
Il piano nello spazio come luogo geometrico
Quella che abbiamo visto finora è una definizione intuitiva di cosa sia un piano nello spazio. Quando studiamo la geometria analitica, però, dobbiamo essere precisi e definire questi nostri enti come dei luoghi geometrici.
Notiamo che ad ogni piano corrisponde un vettore che è perpendicolare ad esso:
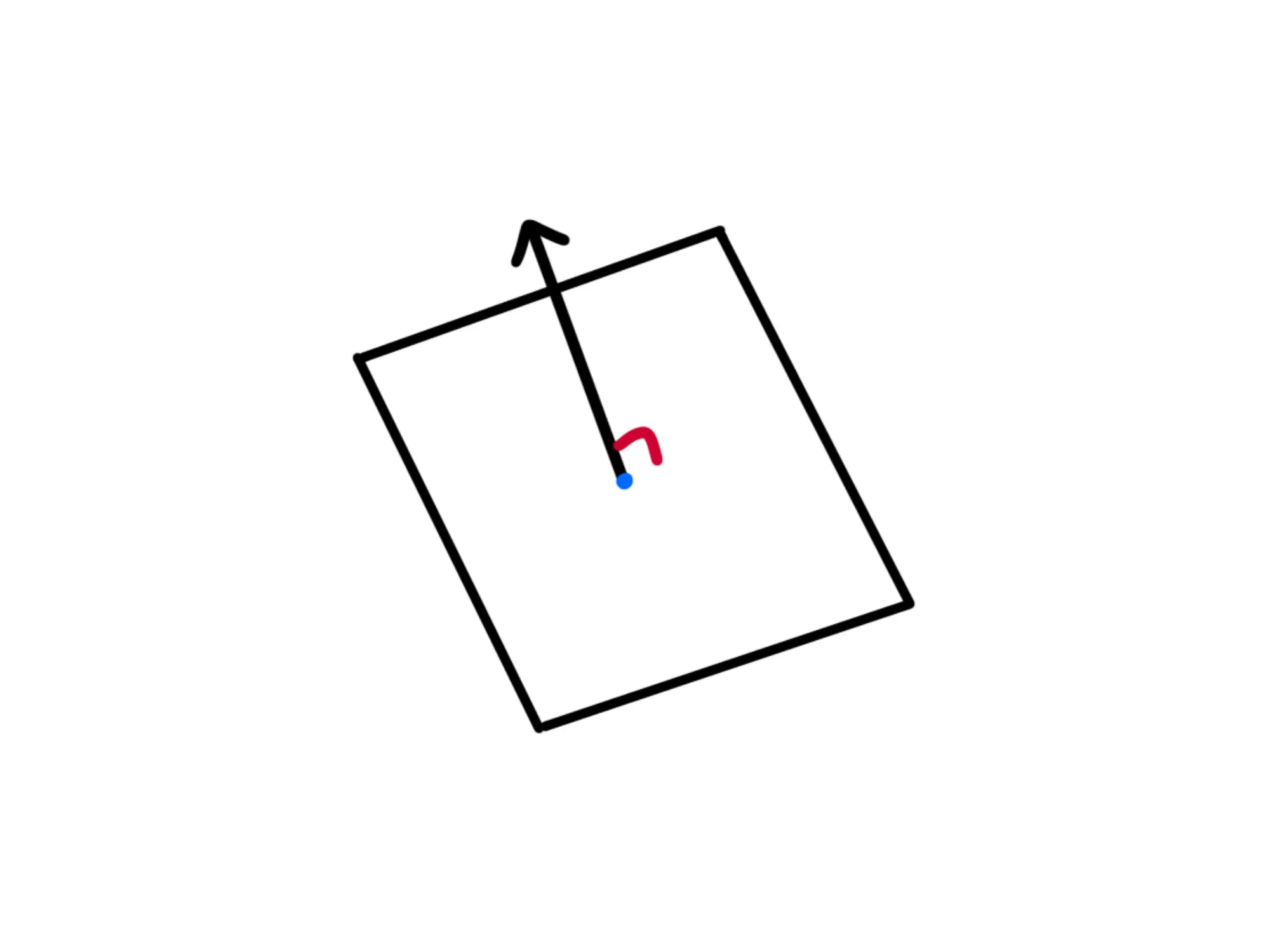
Questo vettore viene chiamato vettore normale al piano (infatti "normale" in questo contesto significa "perpendicolare").
Se dunque prendiamo un vettore normale al piano in un punto P_0, tutti i vettori che posso creare unendo P_0 ad un altro punto del piano devono essere perpendicolari al vettore nomrmale, che chiameremo \overrightarrow{n}:
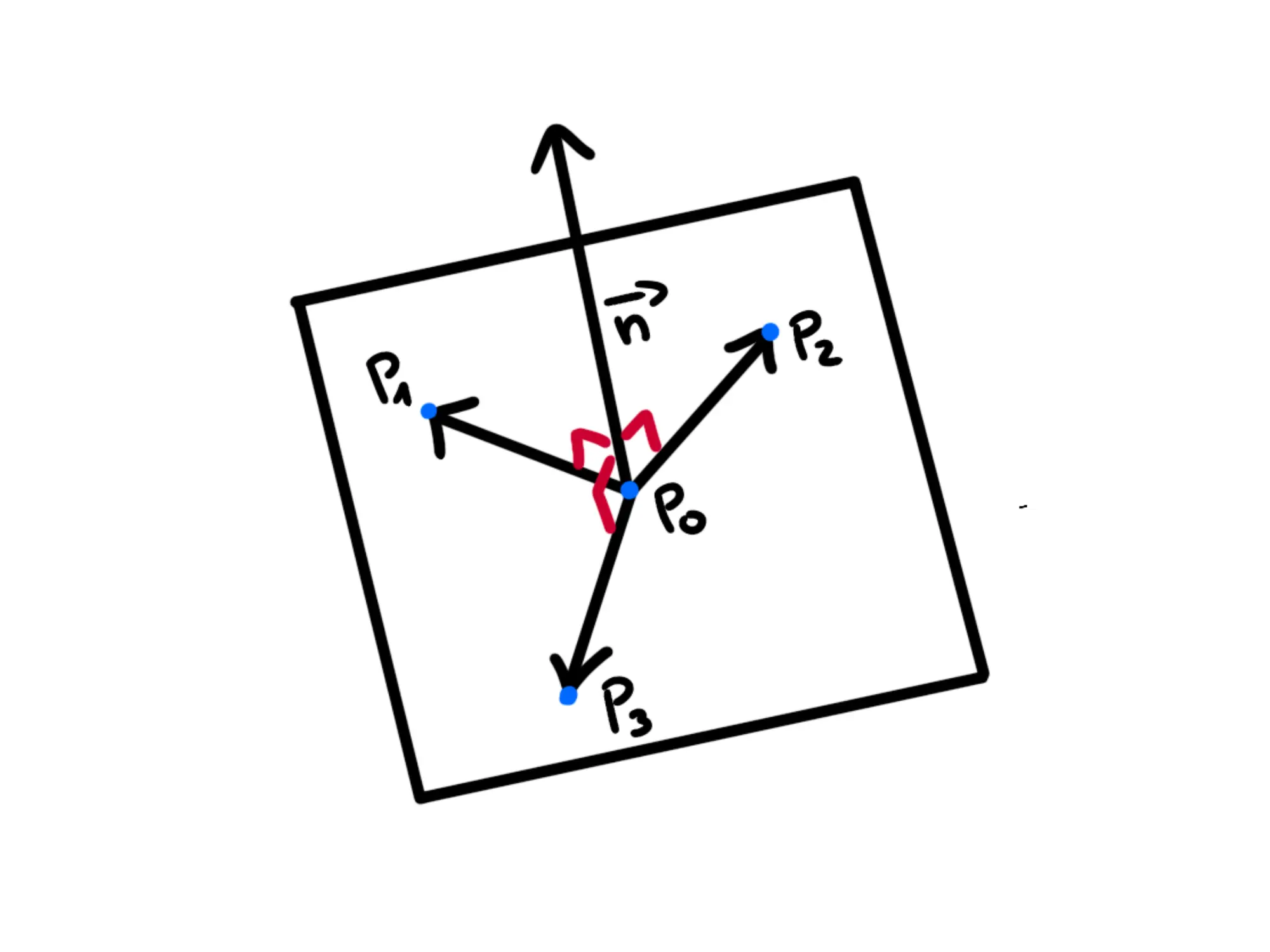
Possiamo dunque definire il piano passante per P_0 e con vettore normale \overrightarrow{n\,} come il luogo geometrico dei punti tali che il vettore che li congiunge a P_0 è perpendicolare a \overrightarrow{n}.
Se dunque prendiamo un generico punto P(x,y,z), affinchè il punto appartenga al piano, il vettore \overrightarrow{P_0P} deve essere perpendicolare a \overrightarrow{n}.
Diamo a P_0 delle coordinate (x_0, y_0, z_0) e chiamiamo a, b e c le entrate del vettore \overrightarrow{n}. Quindi:
\overrightarrow{n} = \left(\begin{array}{l} a \\b \\c \end{array}\right)
\overrightarrow{P_0P} = \left(\begin{array}{l} x-x_0 \\y-y_0 \\ z - z_0 \end{array}\right)
Affinchè questi due vettori siano perpendicolari il loro prodotto scalare deve essere uguale a 0, quindi dobbiamo avere:
\left(\begin{array}{l} a \\b \\c \end{array}\right) \cdot \left(\begin{array}{l} x-x_0 \\y-y_0 \\z-z_0 \end{array}\right) = 0
a(x-x_0) + b(y-y_0) + c(z-z_0) =0
ax -ax_0 + by - by_0 + cz + cz_0 =0
ax + by + cz - ax_0 - by_0 - cz_0 = 0
Ora chiamiamo -ax_0 - by_0 - cz_0 come d ed otteniamo:
ax+by+cz+d=0
Che è proprio l'equazione che avevamo ottenuto prima, solo che adesso l'abbiamo dimostrata in maniera più rigorosa. Adesso sappiamo pure che i coefficienti delle variabili sono le entrate del vettore normale al piano.
Da questo possiamo facilmente determinare la posizione reciproca fra due piani:
Se i due piani sono paralleli, allora anche i due vettori normali devono essere paralleli e quindi il rapporto tra le loro coordinate deve essere costante. Notate che otteniamo la stessa condizione che avevamo ottenuto prima.
Adesso però possiamo sapere pure quando due piani sono perpendicolari. In questo caso, infatti, anche i loro vettori normali devono essere perpendicolari e quindi ci basta verificare se il loro prodotto scalare è uguale a 0.
Distanza punto piano
Per calcolare la distanza punto piano ci basta applicare un'apposita formula che è molto simile alla formula per la distanza punto retta nello spazio con due dimensioni.
Si tratta infatti della stessa formula, solo che dovremo aggiungere cz_0 nel modulo e dovremo aggiungere c^2 nella radice al numeratore.
Se infatti abbiamo un piano di equazione ax+by+cz+d=0 ed un punto P(x_0, y_0, z_0), la distanza tra i due è uguale a:
{|ax_0 + by_0 + cz_0 + d| \over \sqrt{a^2 + b^2 + c^2}}
