Un ente geometrico fondamentale è, come dice la parola, un'entità di base della geometria euclidea. Essi sono il punto, la retta, e il piano.
Il punto non ha alcuna grandezza, ma solo una posizione. Si dice quindi che è adimensionale, o che ha dimensioni.
Viene solitamente indicato con una lettera maiuscola.
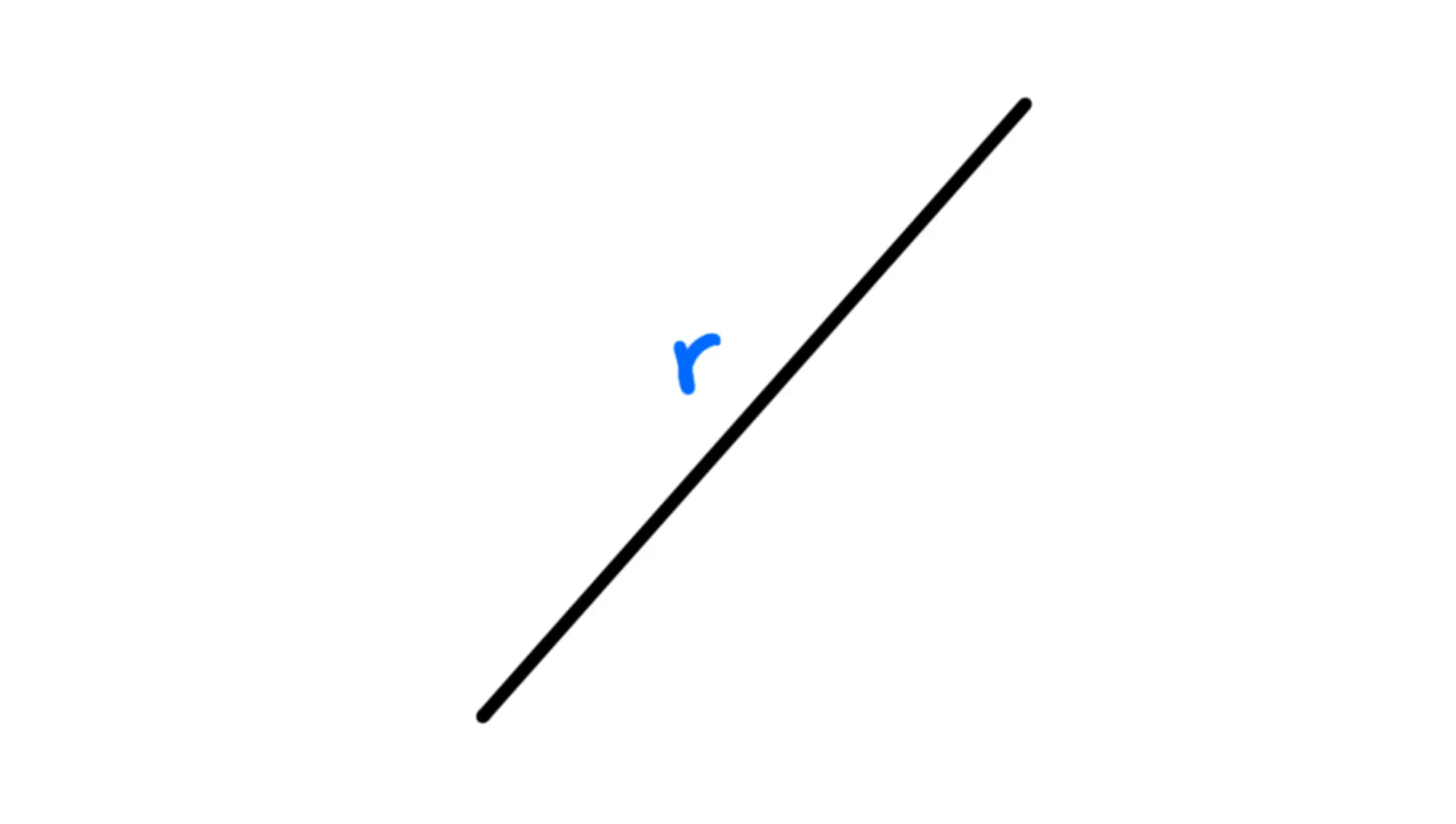
Si indica solitamente con la lettera minuscola.
Il piano è un insieme infinito di punti che formano una superficie piatta, senza spessore e illimitata.
Siccome non possiamo disegnare un piano, perché occuperebbe infinito spazio, lo schematizziamo così:
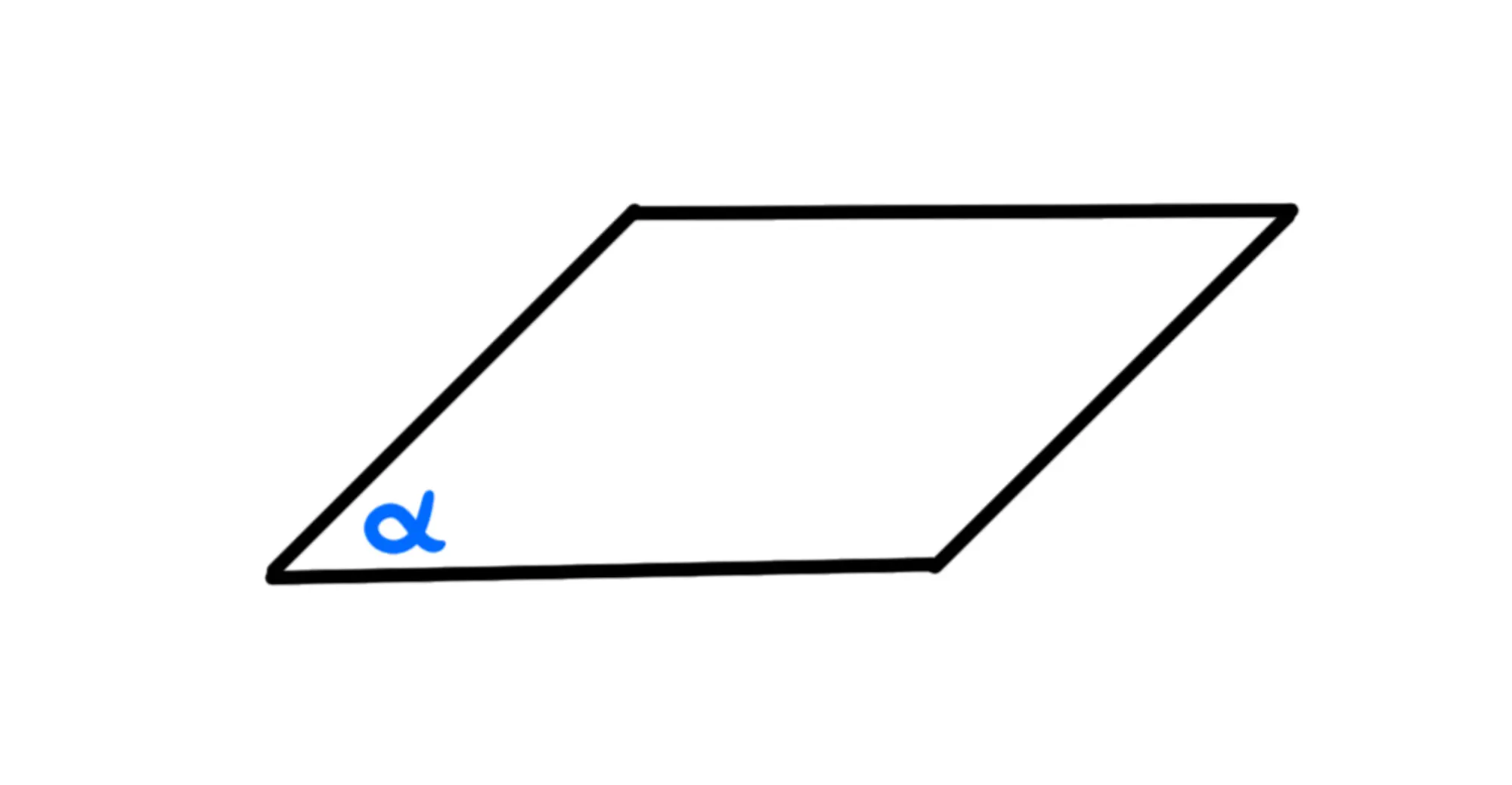
Il piano si indica solamente con una lettera minuscola dell'alfabeto greco.
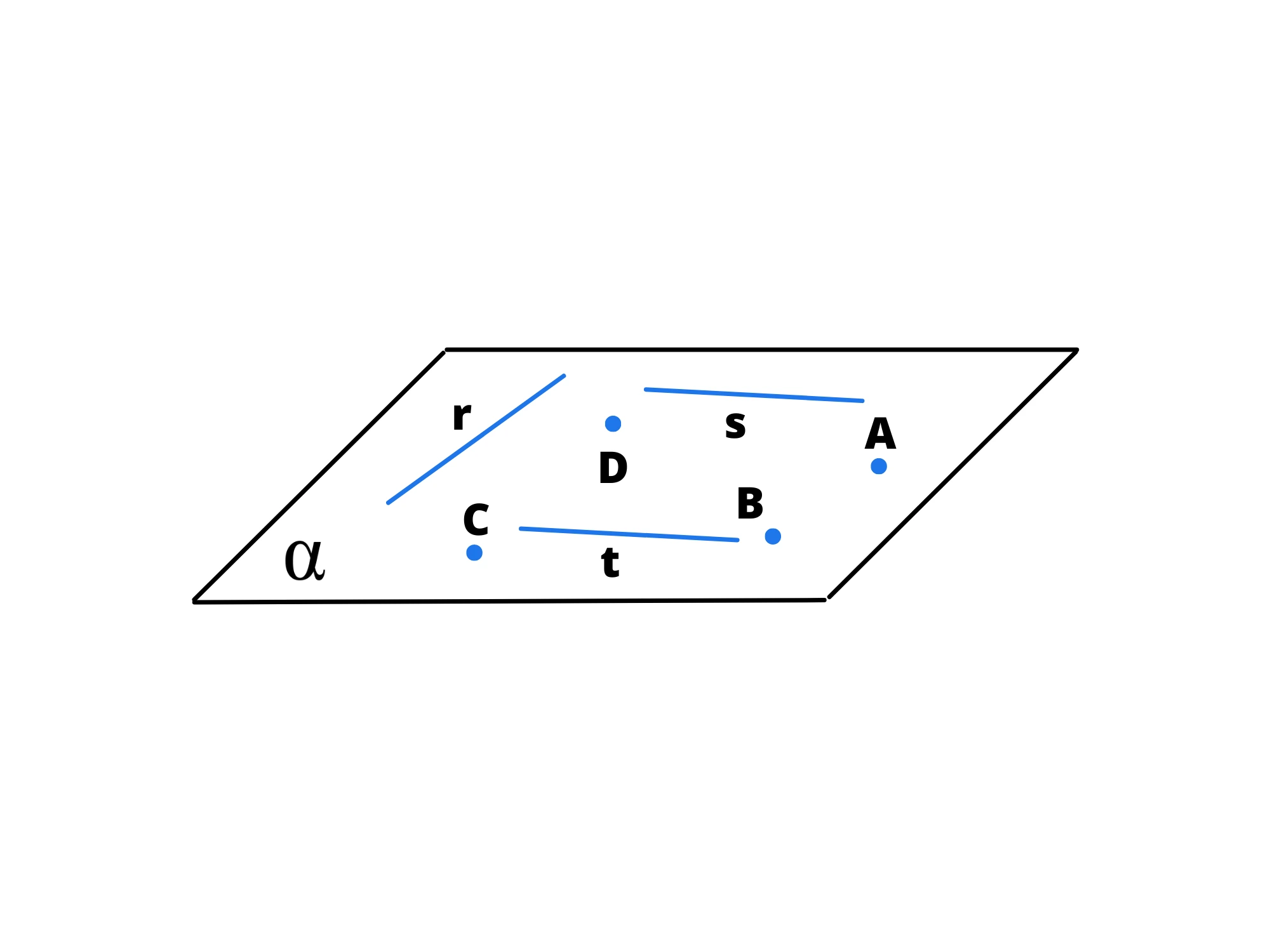
2. Una retta contiene infiniti punti.
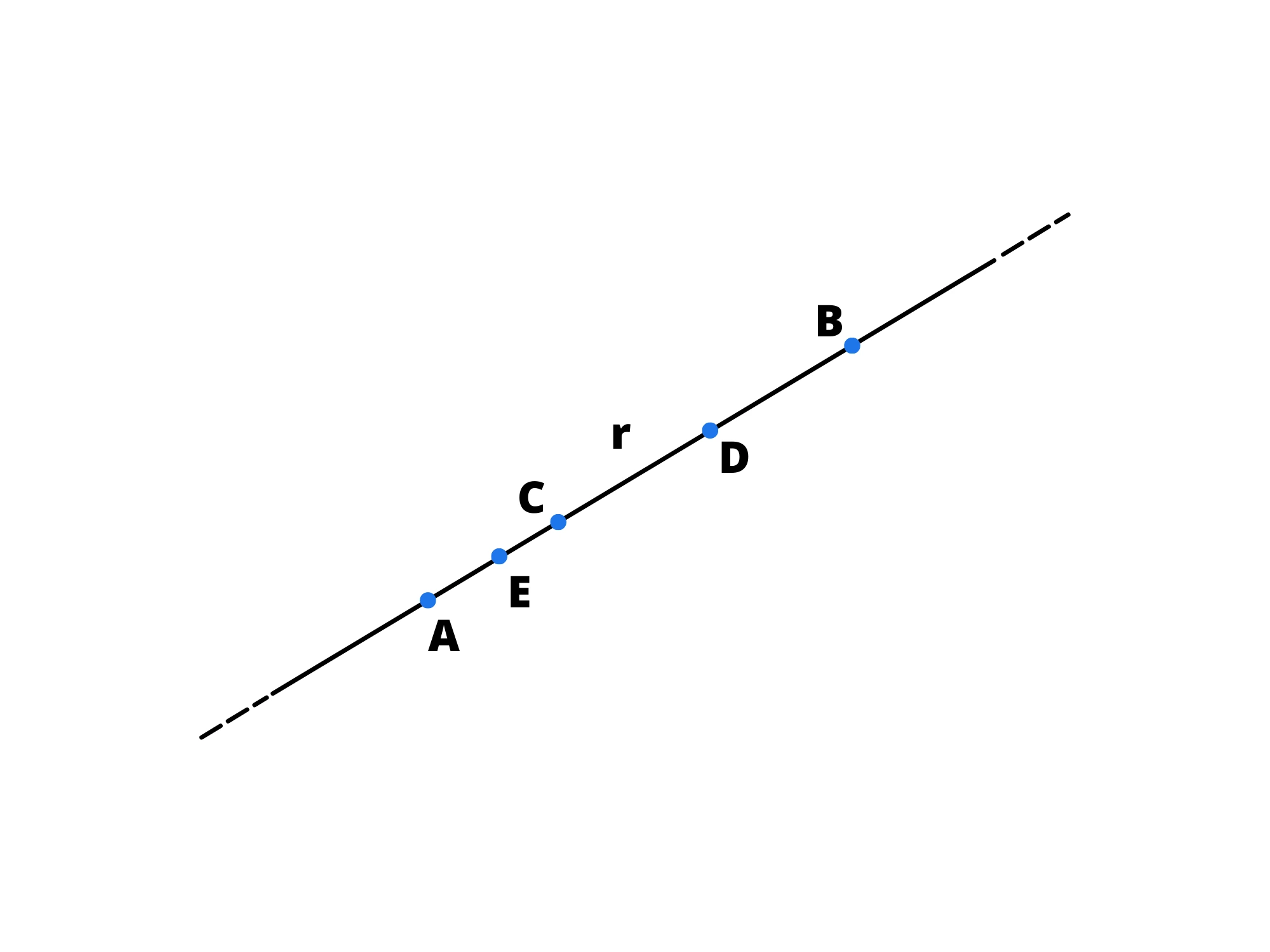
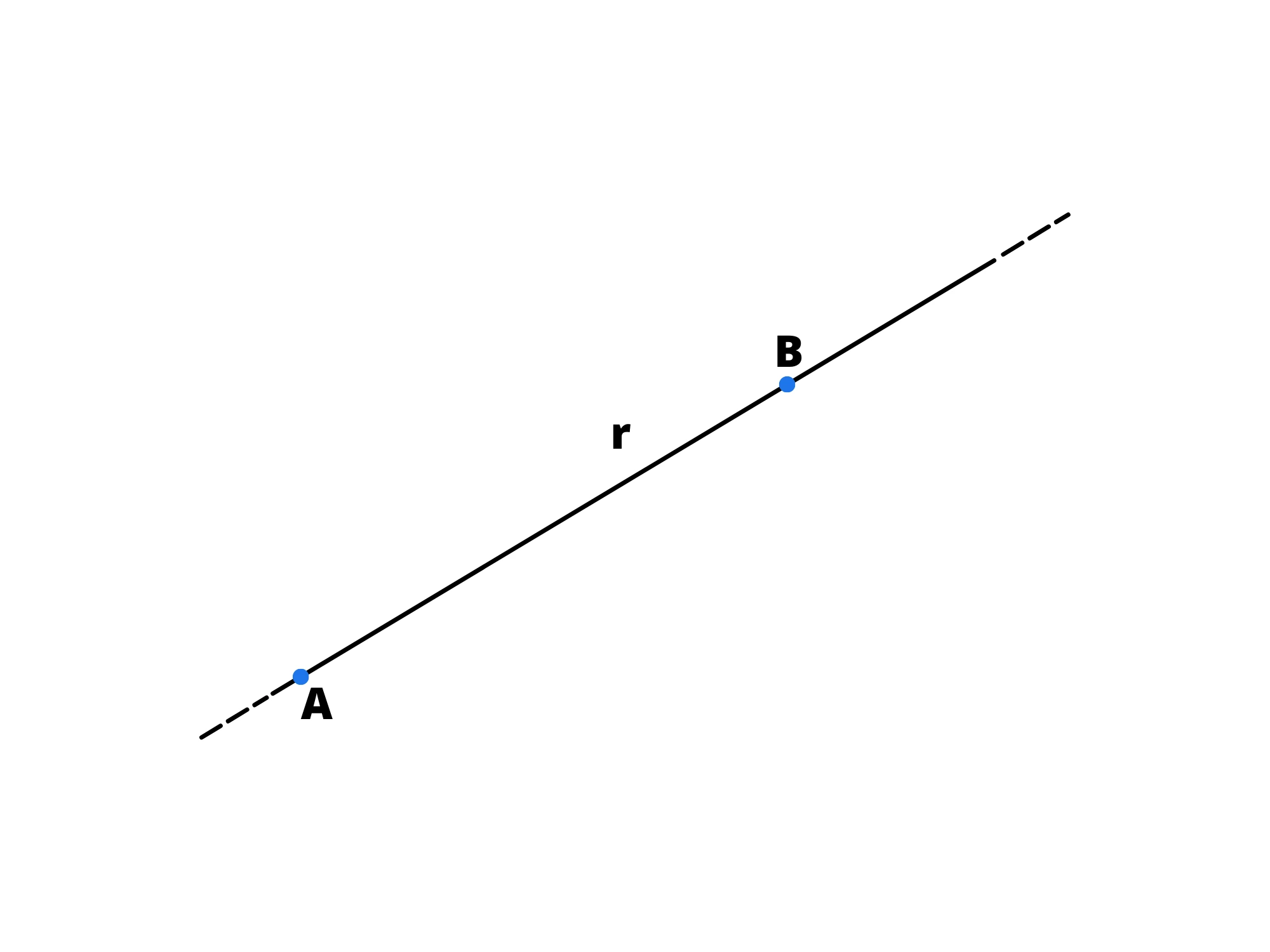
3. Per due punti distinti passa una e una sola retta.
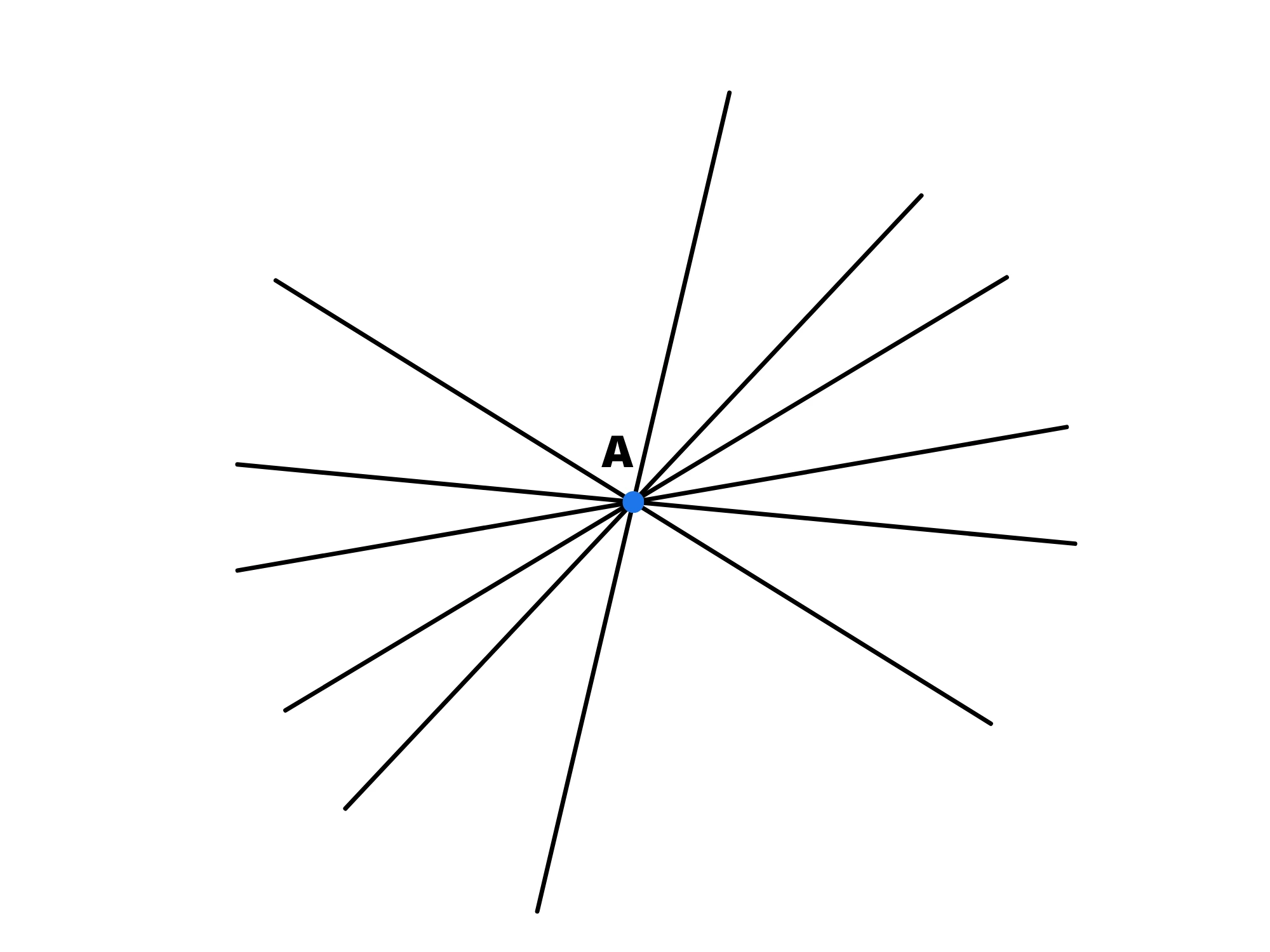
4. Per un punto passano infinite rette.
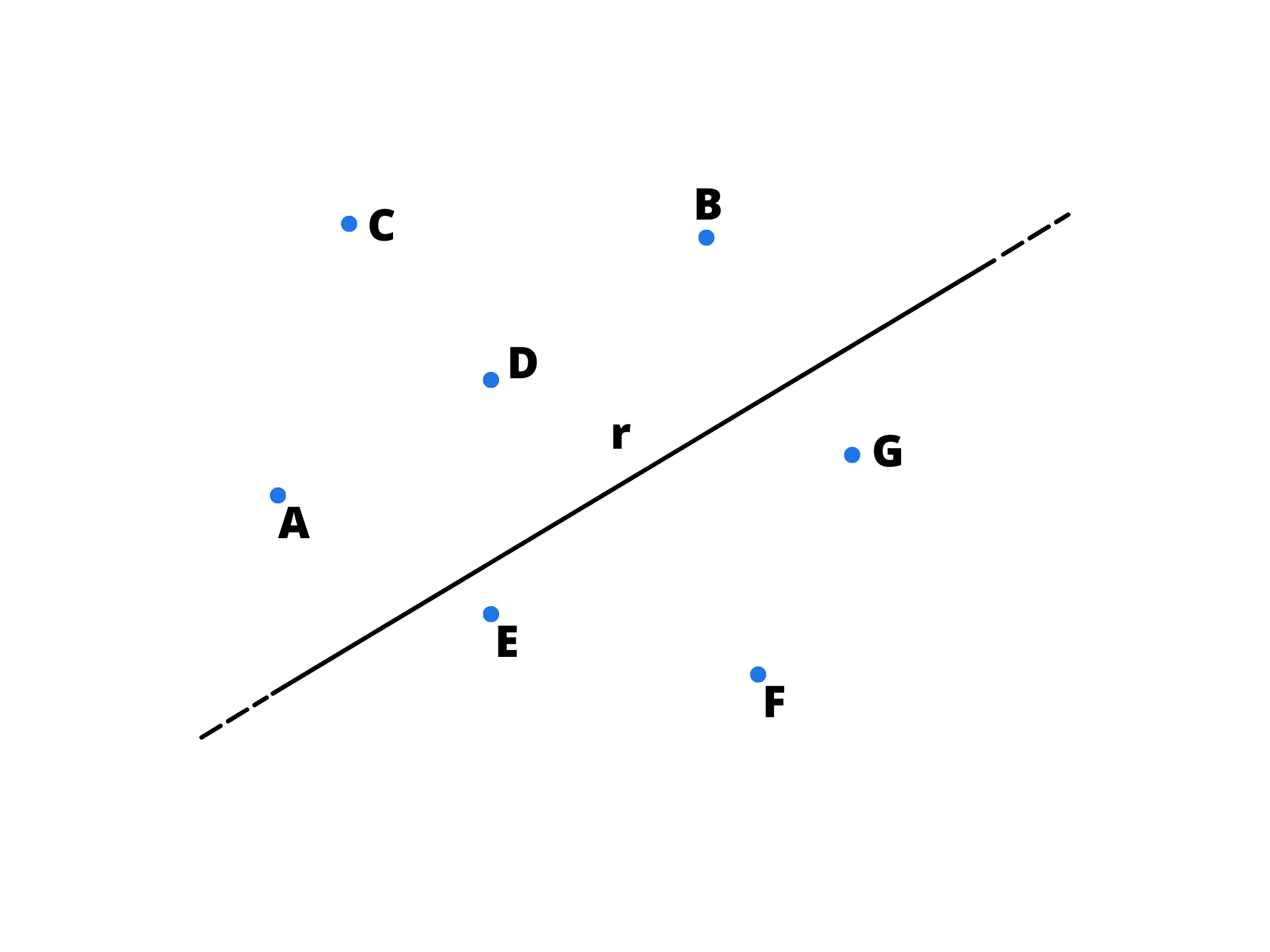
5. Esistono infiniti punti non appartenenti alla stessa retta.
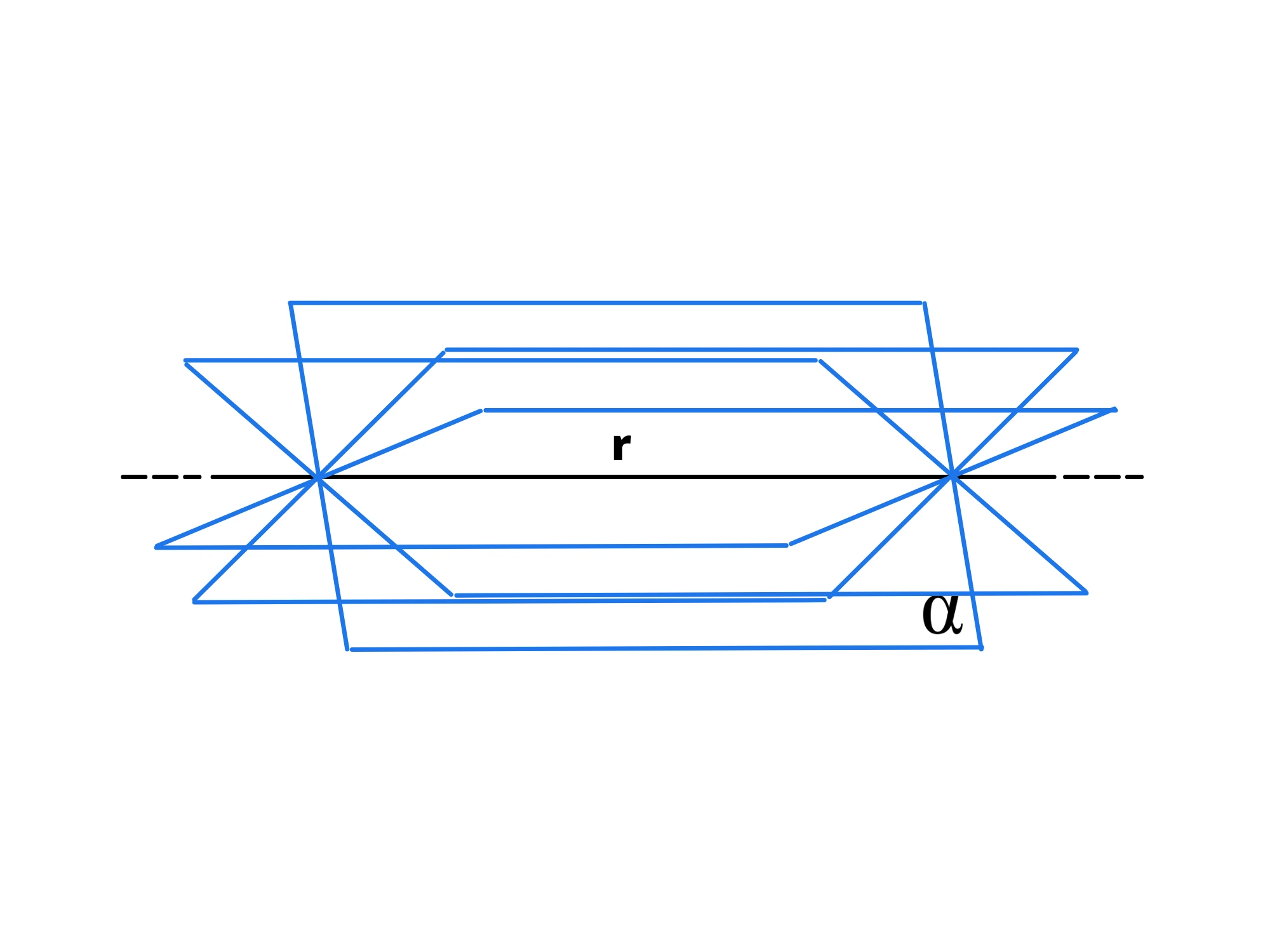
6. Per una retta passano infiniti piani.
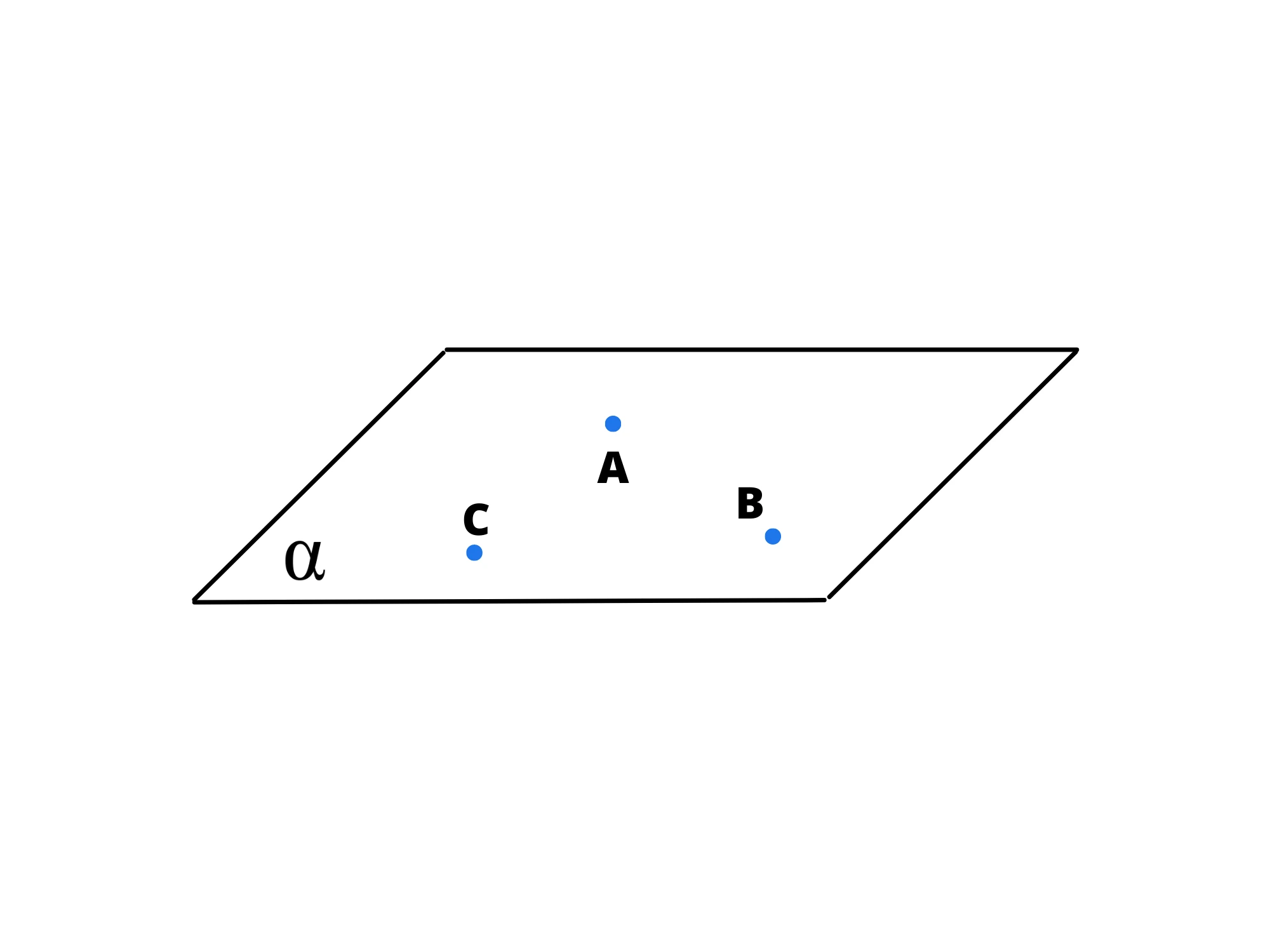
7. Per punti non allineati passa uno e un solo piano.
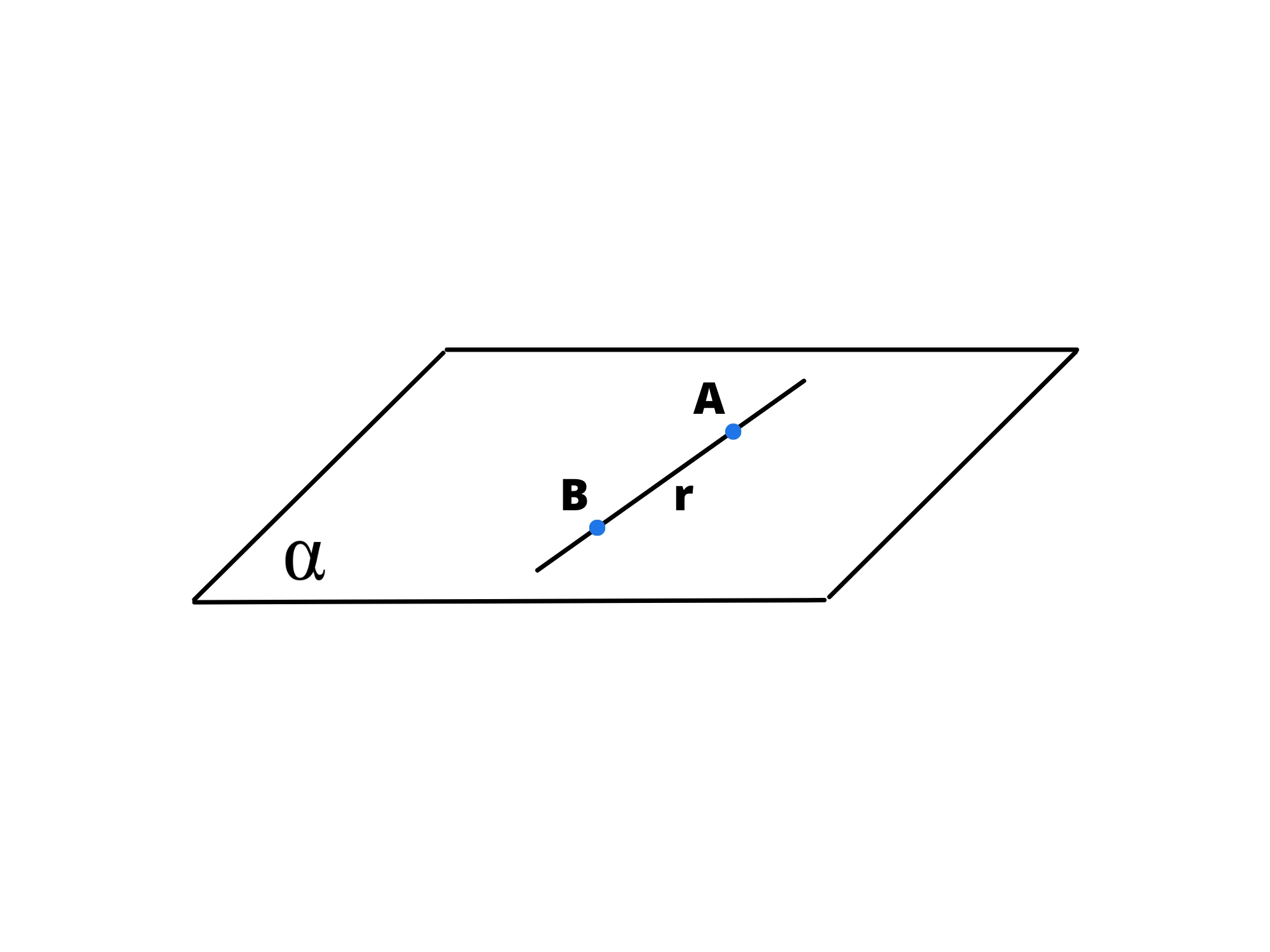
8. Se almeno due punti di una retta appartengono a un piano, allora l'intera retta è contenuta nel piano.
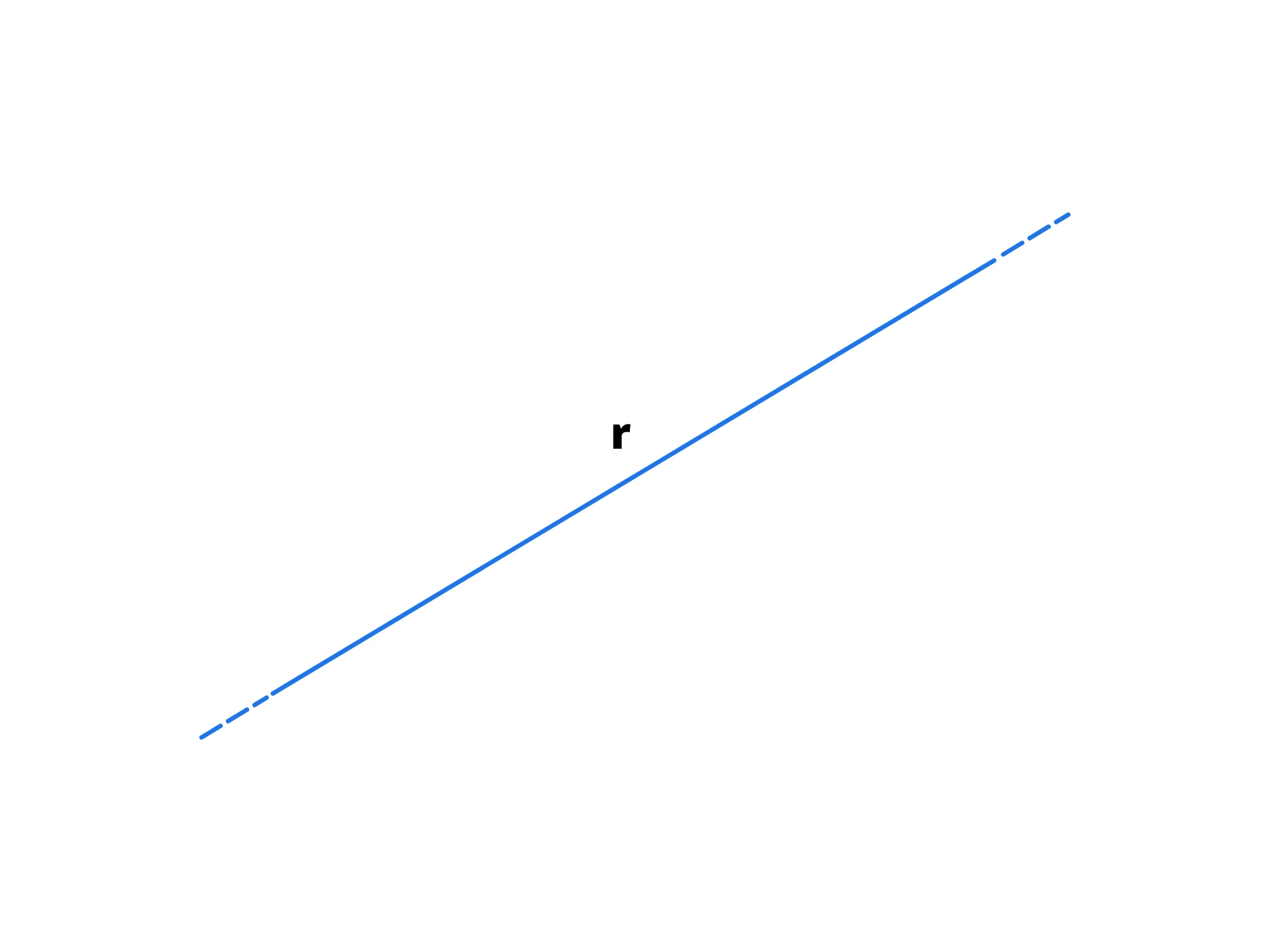
Talvolta, per far comprendere che la retta tende all'infinito, potrebbe essere richiesto di tratteggiarne gli estremi:
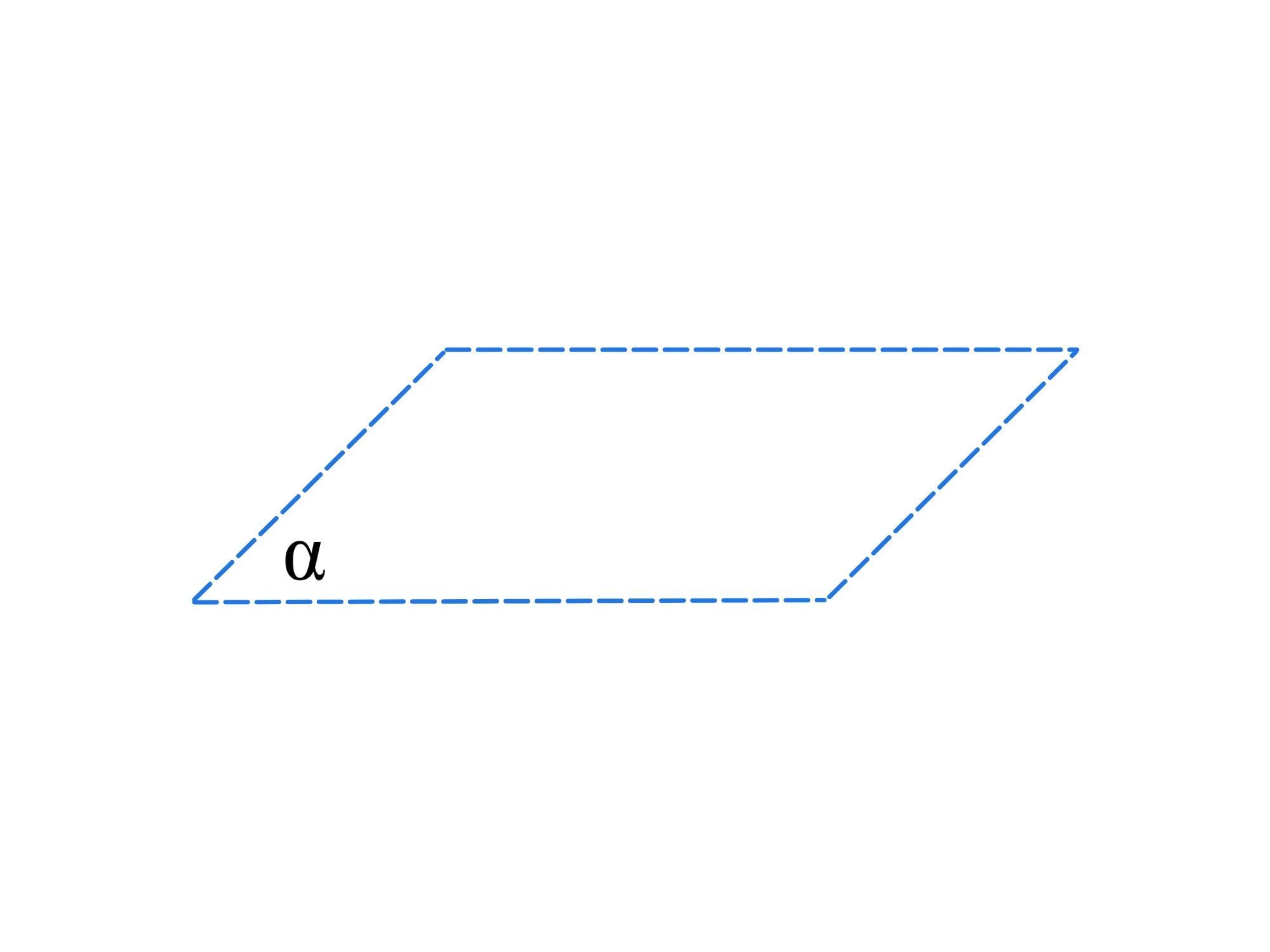
O di tratteggiare i bordi di un piano:
Bisogna notare che né il punto, né la retta, né il piano esistono nel mondo reale, ma sono concetti astratti. Infatti, per quanto ci si possa sforzare a fare un punto il piccolo possibile, sarà in realtà sempre un piccolo cerchio.
