Momento di inerzia e accelerazione angolare

Accelerazione angolare

Quando sto facendo ruotare un corpo, esso girerà di un certo angolo $\displaystyle { \Delta \theta }$ in un tempo $\displaystyle { \Delta t. }$

Avevamo già visto nel moto circolare uniforme che chiamiamo velocità angolare il rapporto tra questi due e la si indica con la lettera greco $\displaystyle { \omega }$ (omega):

$\displaystyle { \omega = {\Delta \theta \over \Delta t} }$

La velocità angolare è un vettore, dunque ha pure una direzione ed un verso. La direzione è la retta perpendicolare al piano di rotazione e il verso è entrate se stiamo girando in senso orario, uscente se in senso antiorario:

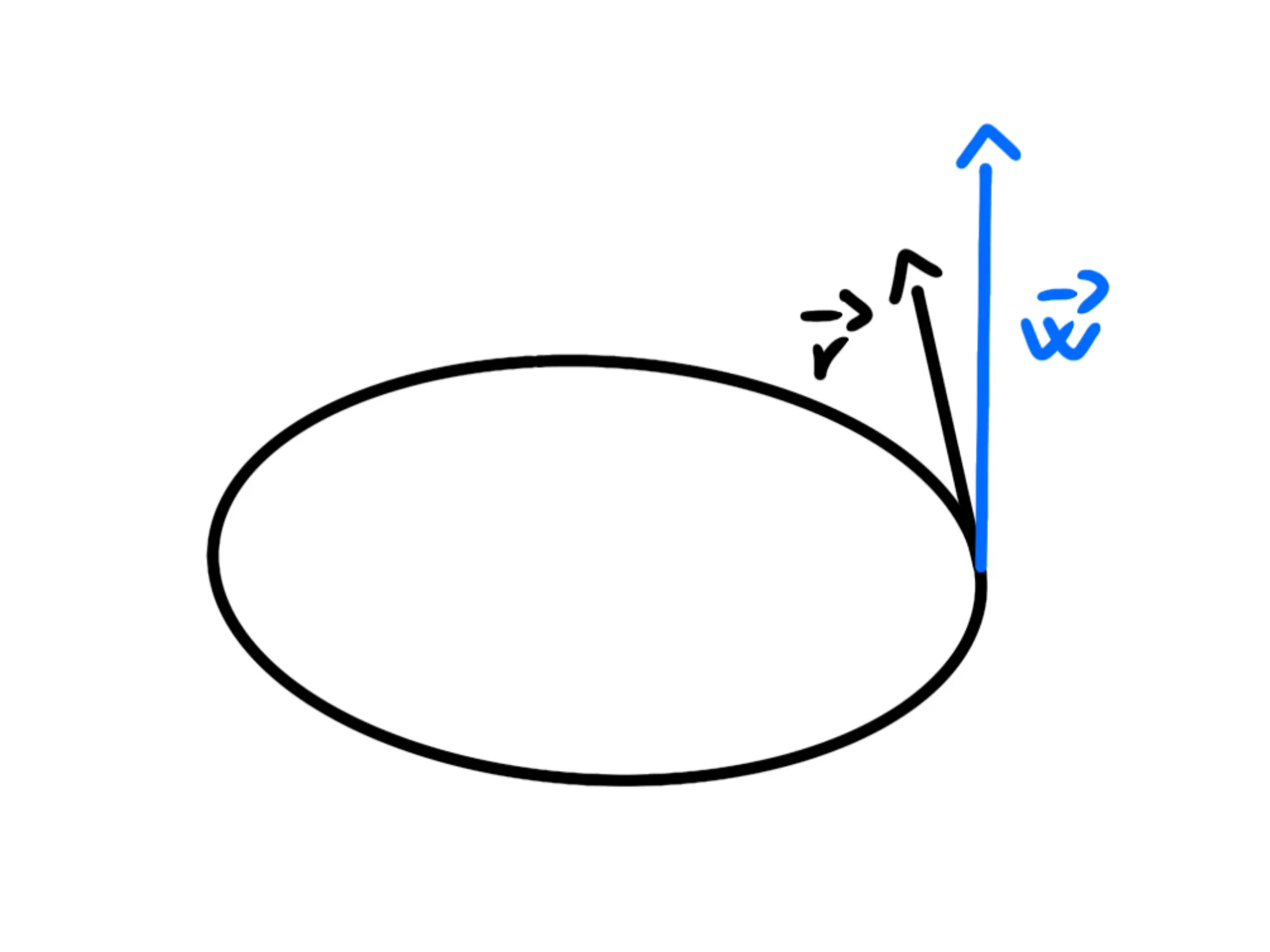
Nel moto circolare uniforme $\displaystyle { \overrightarrow{\omega} }$ era costante, ma se prendo un disco che sta girando e gli do una spinta, comincerà a girare ancora più velocemente. Cioè posso variare la velocità angolare di un corpo.

Per studiare questo cambiamento, introduciamo una nuova grandezza fisica, chiamata accelerazione angolare $\displaystyle { \overrightarrow{\alpha}, }$ che sarà uguale alla variazione della velocità angolare $\displaystyle { \Delta \omega }$ avvenuta in un tempo $\displaystyle { \Delta t: }$

$\displaystyle { \alpha = {\Delta \omega \over \Delta t} }$

Anche l'accelerazione angolare è un vettore ed ha la stessa direzione e verso della velocità angolare:

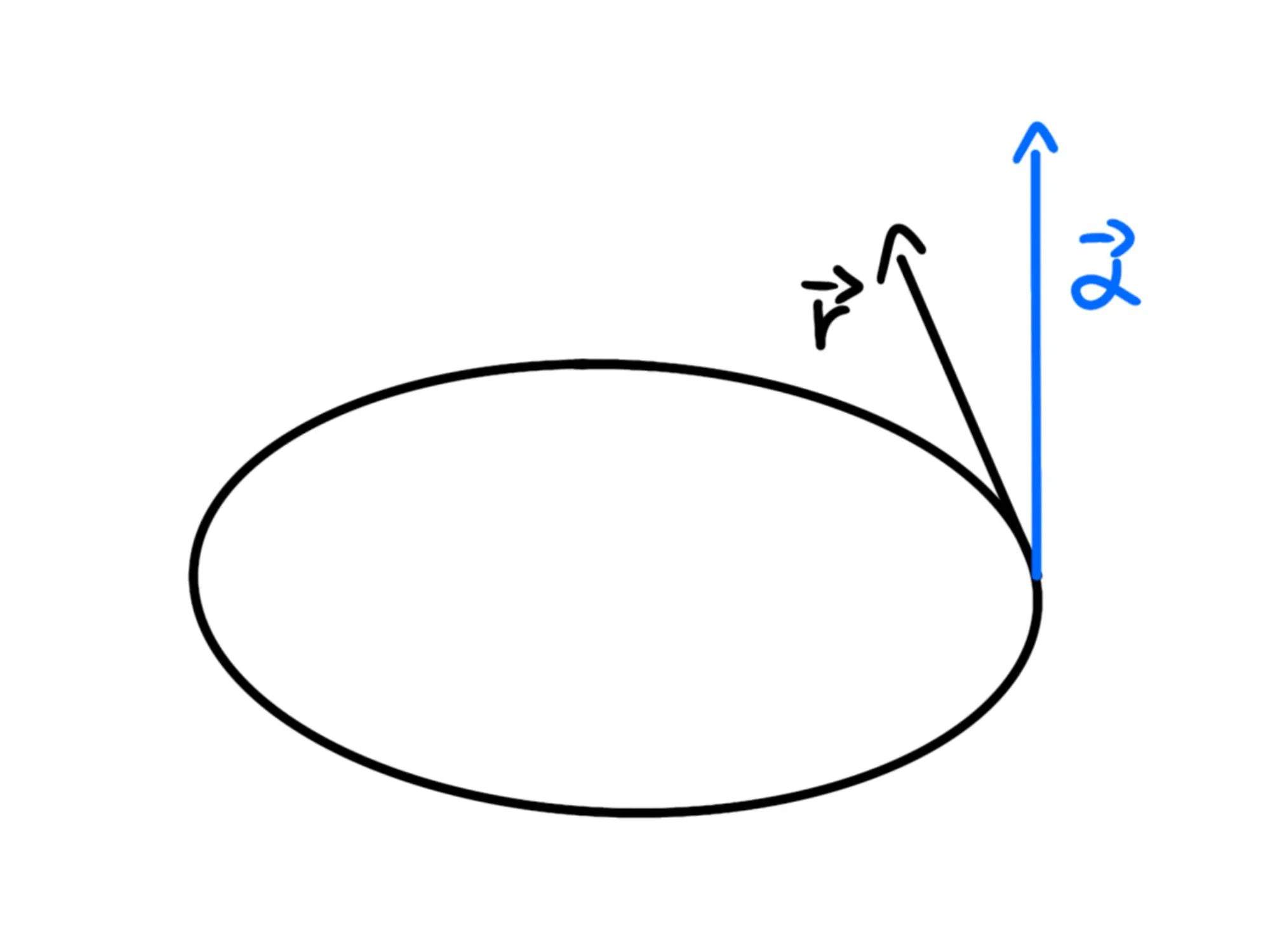
Come facciamo a generare un'accelerazione angolare? Nel caso di prima avevamo spinto il disco. In generale, dobbiamo applicare una forza e questa forza non deve avere un momento nullo.

Infatti, facendo esperimenti, si può notare che l'accelerazione angolare è direttamente proporzionale al momento totale delle forze applicate al corpo:

$\displaystyle { \overrightarrow{M} \propto \overrightarrow{\alpha} }$

Il simbolo $\displaystyle { \propto }$ indica, appunto, che le due grandezze sono direttamente proporzionali. In generale vuol dire anche che il loro rapporto è uguale ad una certa costante, che chiameremo $\displaystyle { I: }$

$\displaystyle { {\overrightarrow{M}\over \overrightarrow{\alpha}} = I }$

O anche:

$\displaystyle { \overrightarrow{M} = I \overrightarrow{\alpha} }$

Ma cos'è questa $\displaystyle { I? }$ Facendo degli esperimenti si nota che dipende sia dalla massa dell'oggetto, ma anche dalla sua forma. Chiamiamo questa quantità come momento di inerzia e siccome si tratta di un concetto abbastanza importante, ora lo studieremo in maniera più approfondita:

Momento di inerzia

Nella dinamica traslazionale, avevamo visto che un certo corpo oppone una certa resistenza a modificare il suo stato di quiete o il suo moto rettilineo uniforme. Avevamo chiamato queta quantità massa inerziale (sarebbe cioè la massa).

Allo stesso modo, un corpo che si trova in uno stato di quiete o in un moto circolare uniforme, opporrà una certa resistenza quando si prova a modificare la sua rotazione.

Chiamiamo questa quantità momento di inerzia e la indichiamo con la lettera $\displaystyle { I. }$

Prima ancora di scendere nel dettaglio per vedere come calcolarlo, vogliamo farvi notare l'analogia presente tra la seconda legge della dinamica e la legge che avevamo trovato nel capitolo precedente:

$\displaystyle { \overrightarrow{F} = m\overrightarrow{a} }$

$\displaystyle { \overrightarrow{M} = I\overrightarrow{\alpha} }$

Cioè abbiamo soltanto sotituito le grandezze fisiche con le loro corrispettive nella dinamica rotazionale e la legge continua ad essere vera. Questo è solitamente sempre vero e ne vedremo altri casi quando studieremo il momento angolare.

Ora passiamo a studiare più approfonditamente il momento di inerzia:

Cominciamo notando che il momento di inerzia non dipende soltanto dal corpo, ma anche dall'asse rispetto al quale lo stiamo facendo ruotare.

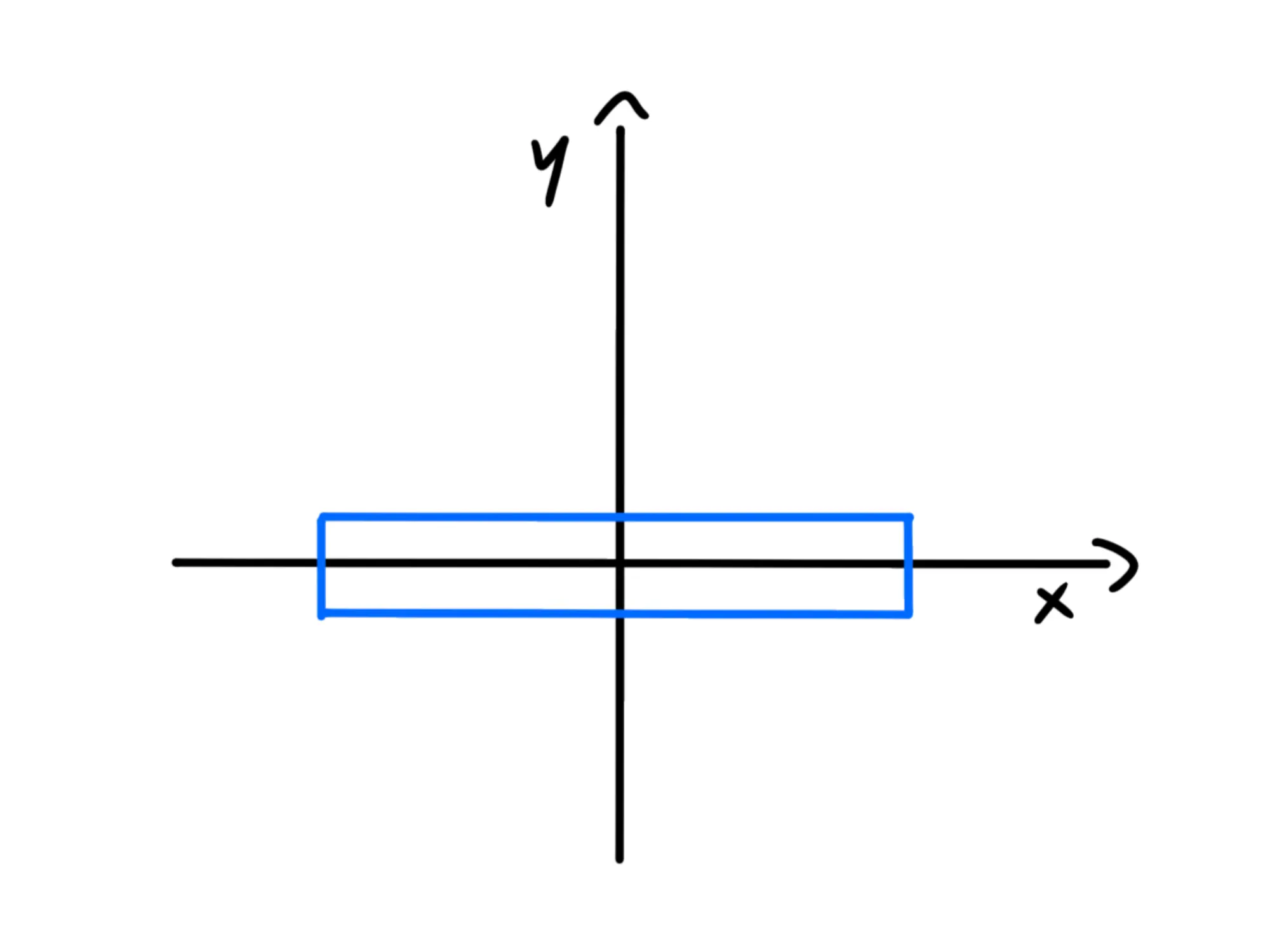
Nel grafico, il momento di inerzia rispetto all'asse $\displaystyle { x }$ è diverso da quello rispetto all'asse $\displaystyle { y. }$

Detto questo, come si calcola effettivamente?

Iniziamo dal caso più semplice: quello di un punto materiale.

Prendiamo un punto $\displaystyle { P }$ di massa $\displaystyle { m }$ che sta ruotando intorno ad un origine $\displaystyle { O }$ ad una certa distanza $\displaystyle { r: }$

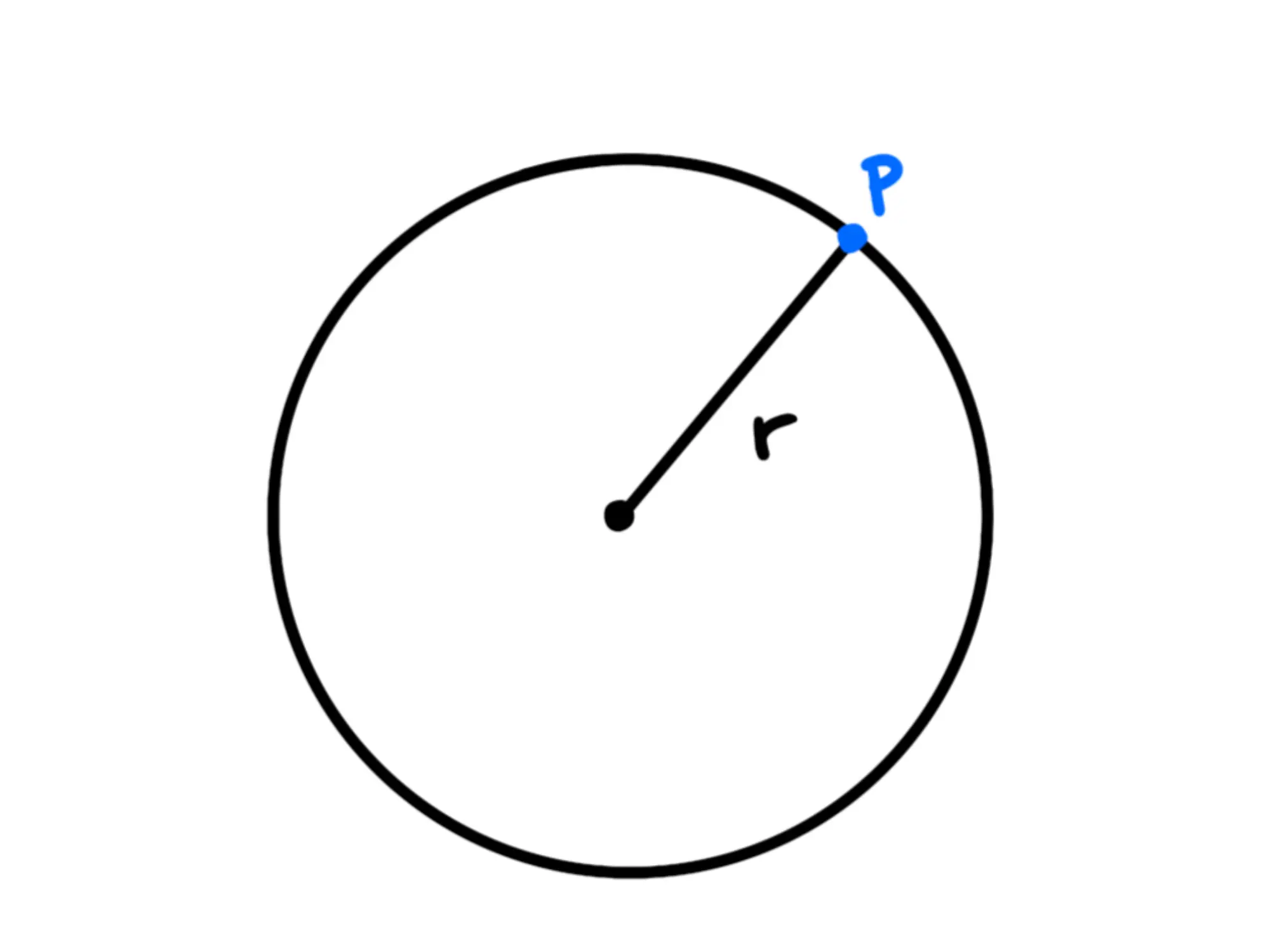
In tal caso il momento di inerzia del punto di può calcolare come il prodotto tra la sua massa e la distanza dall'origine al quadrato:

$\displaystyle { I = mr^2 }$

Se quindi ho un corpo che sta ruotando intorno ad un asse $\displaystyle { x, }$ dovrò calcolare il momento di inerzia di ogni suo singolo punto e sommarli insieme.

Siccome non possiamo sommare manualmente infinite quantità, possiamo prendere quantità non infinitamente piccole ma solo abbastanza piccole da poterle più o meno approssimare ad un punto.

Se dividiamo quindi il corpo in $\displaystyle { N }$ volumetti abbastanza piccoli da poterli approssimare a punti, il momento sarà la somma dei momenti di inerzia dei singoli volumetti:

$\displaystyle { I = \sum_{i = 1}^{N} m_i {r_1}^2 }$

Per ottenere una buona approssimazione, avremo comunque bisogno di sommare centinaia di pezzetti, il che richiederebbe troppo tempo. Avete dunque due alternative:

La prima è di usare il calcolo integrale. In questo caso basterà riscrivere la formula di prima come un integrale e calcolarlo:

$\displaystyle { I = \int_V r^2 dm }$

Dove $\displaystyle { V }$ è il volume del corpo su cui stiamo integrando. Un ulteriore vantaggio di usare l'integrale al posto delle sommatoria è che dividendo in questo modo il corpo in parti infinitesime, non otteniamo soltanto un'approssimazione ma proprio il valore esatto.

Se però non avete ancora studiato il calcolo integrale (che sarà il caso del 99% di voi), allora vi toccherà impararvi a memoria i valori più comuni. Tanto i prof vi chiederanno solo i casi particolari, come le sfere, i cilindri e i parallelopipedi.

Forniamo di seguito una tabella con questi valori noti (dove $\displaystyle { M }$ indica la massa totale del corpo):

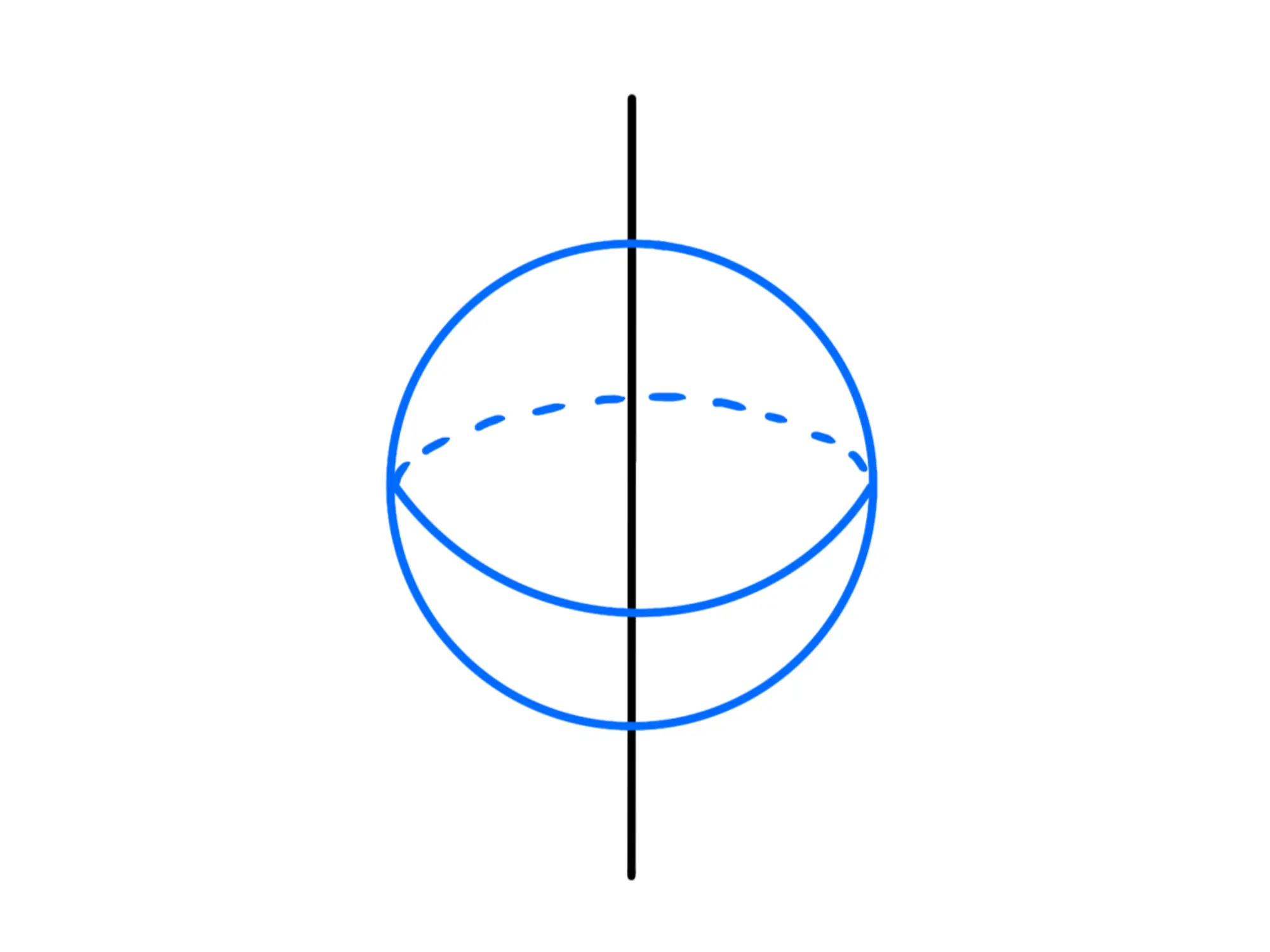
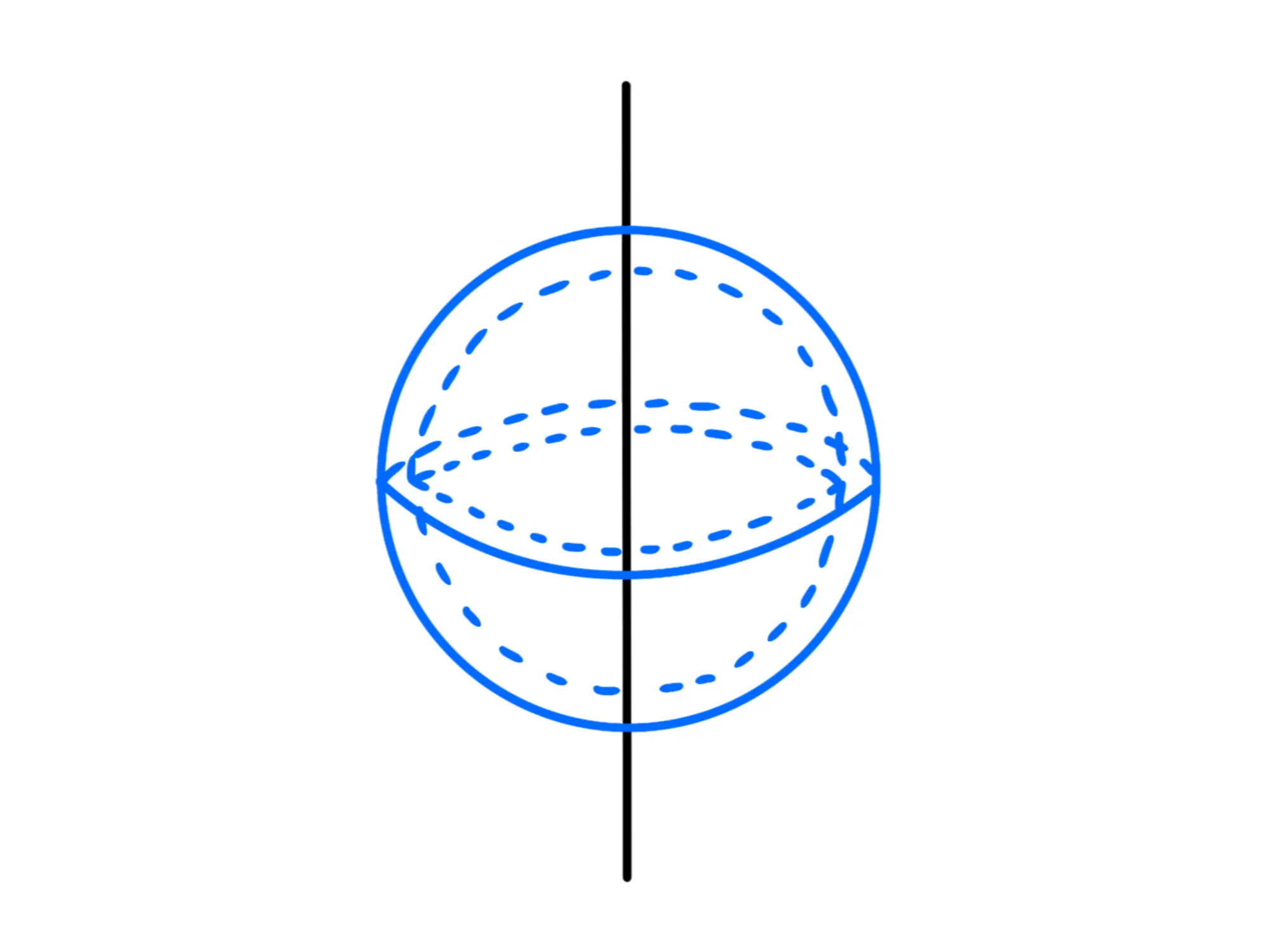
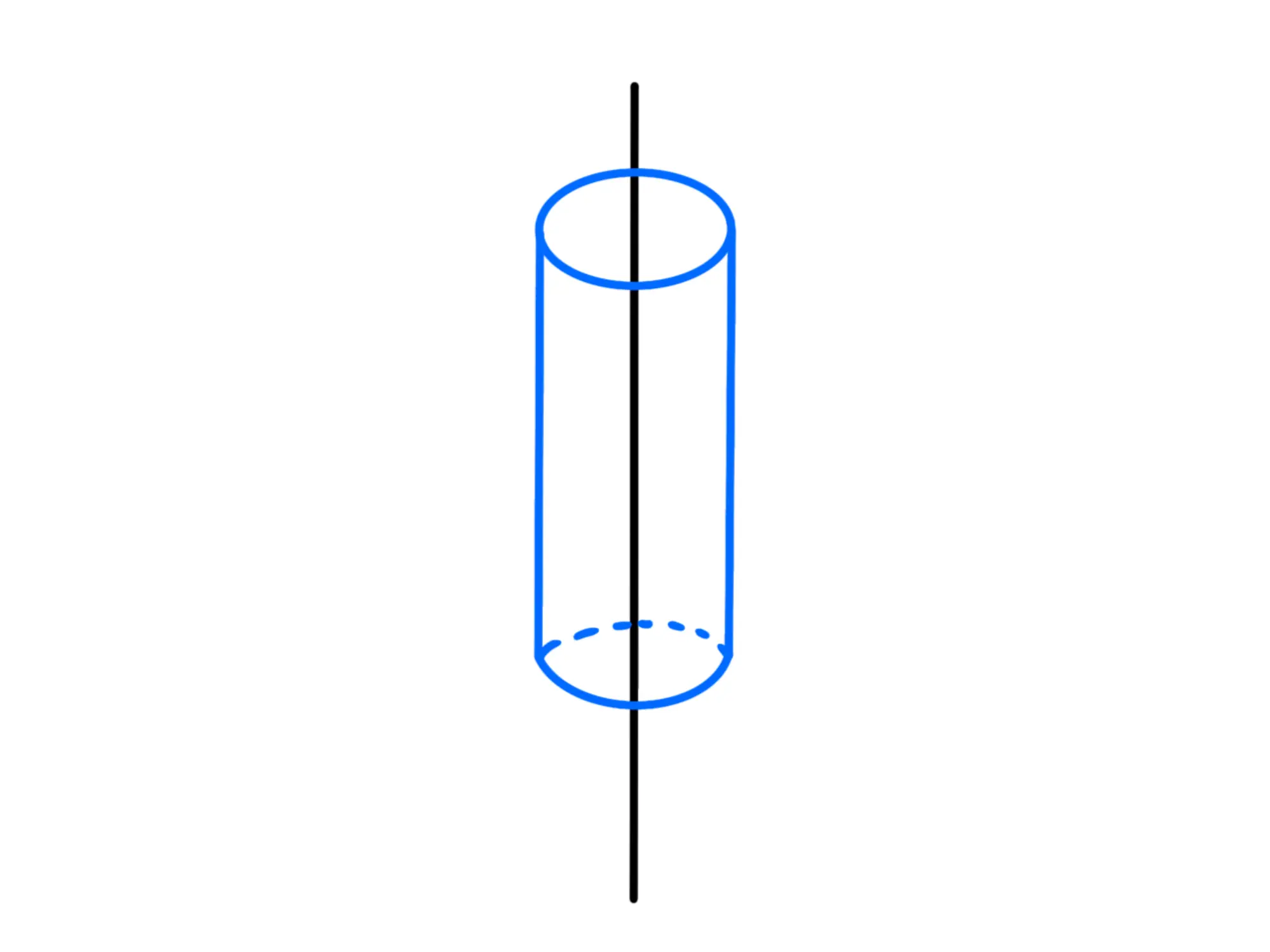
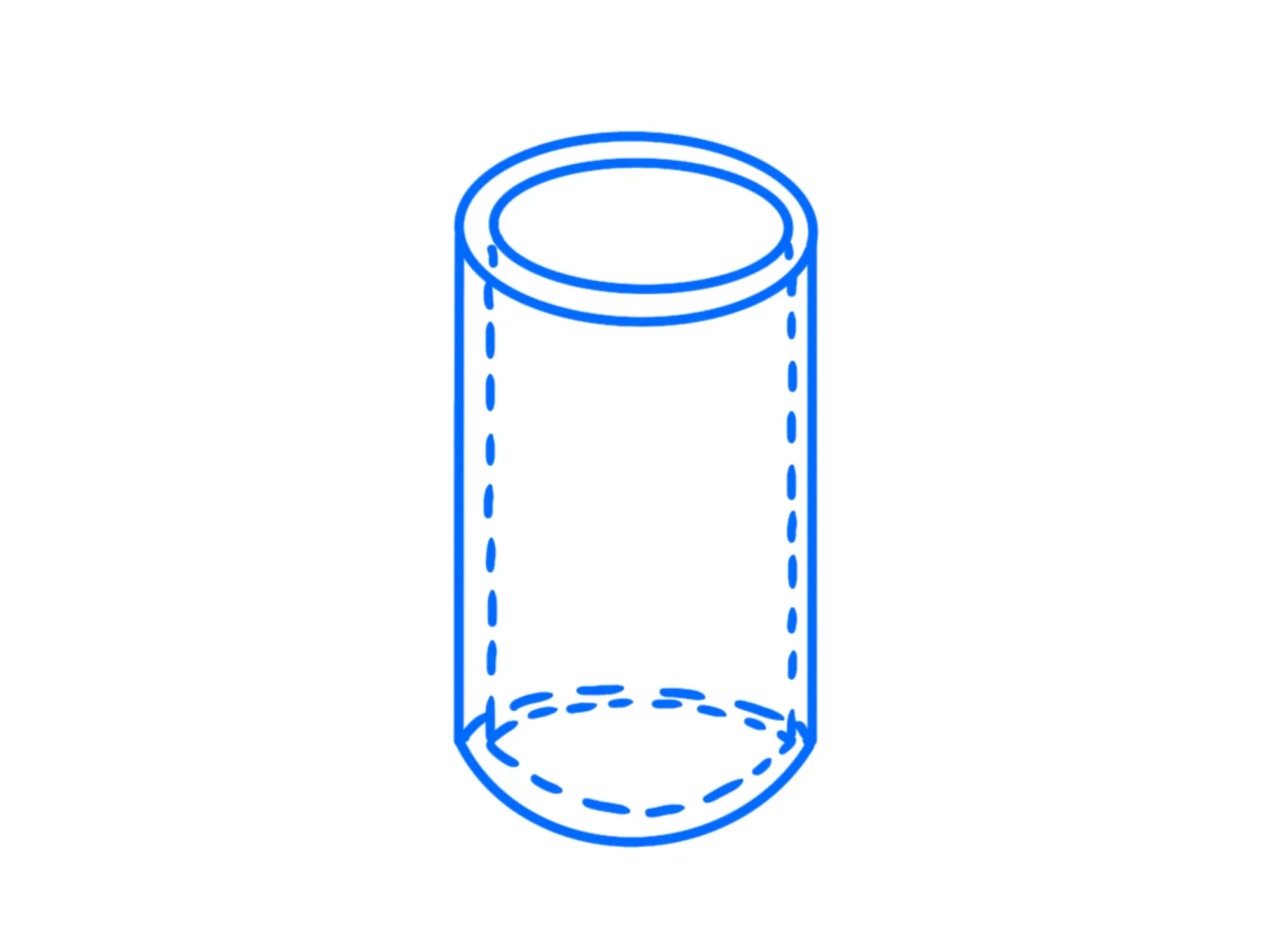
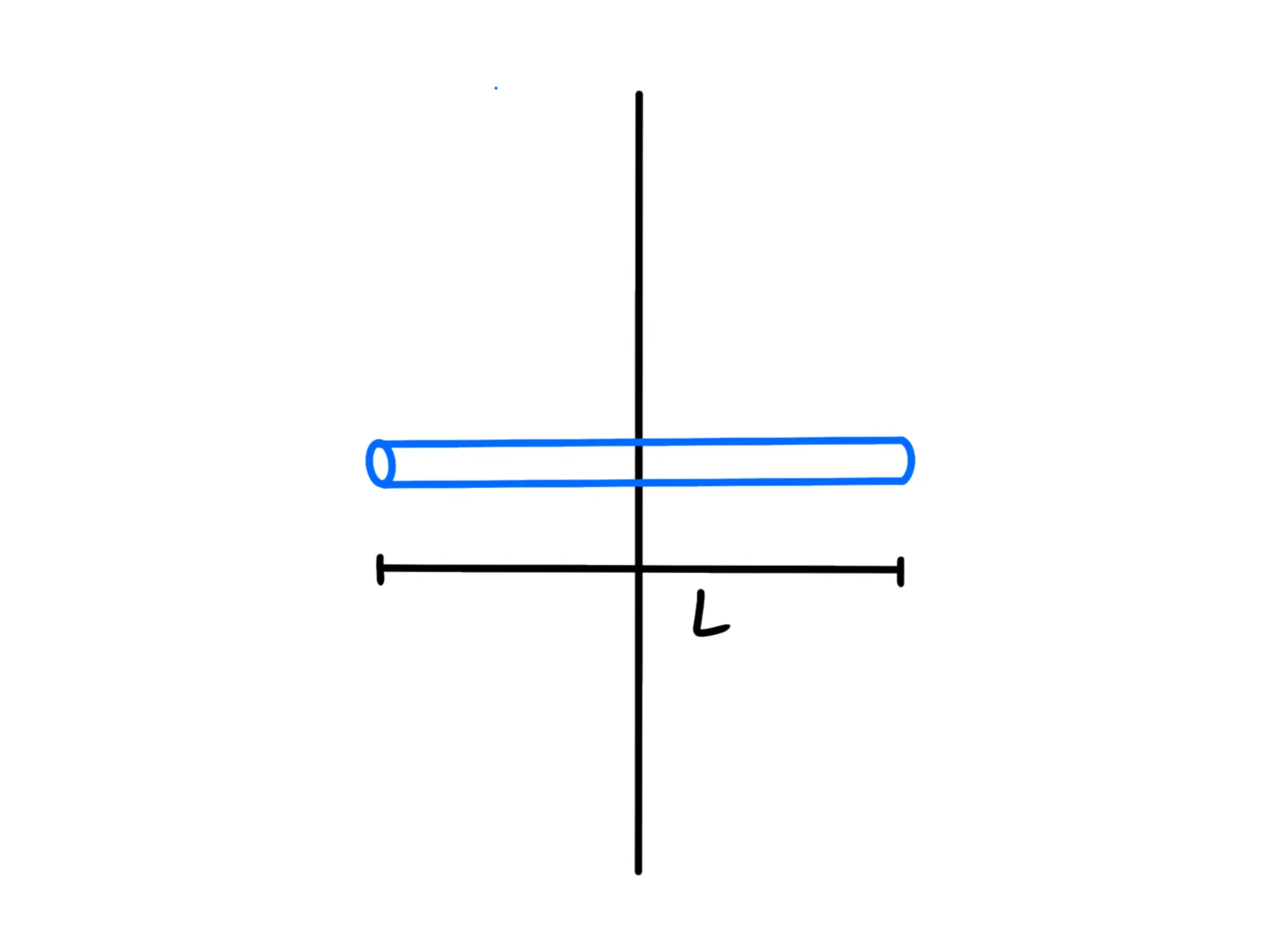
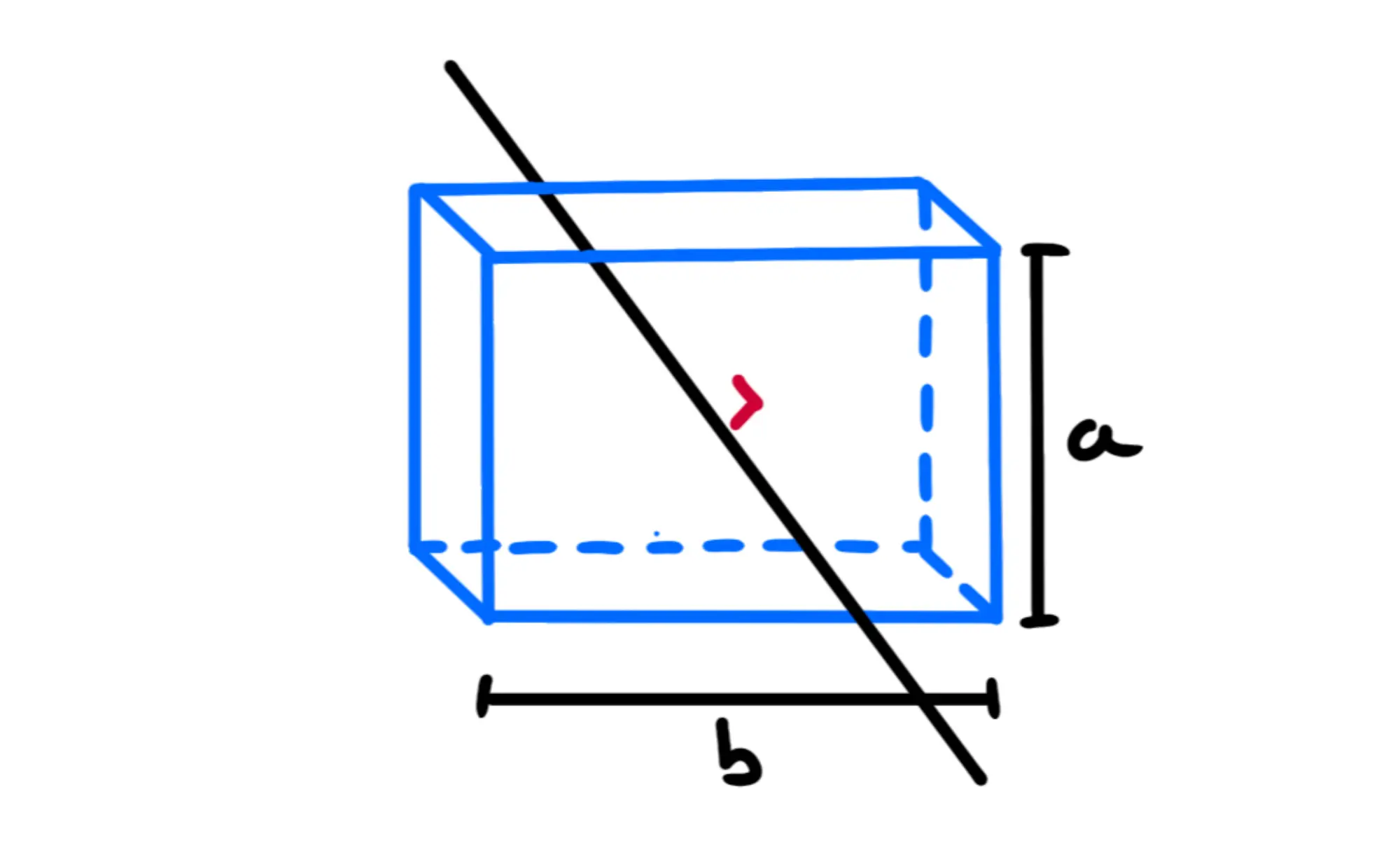
*Notate che questo è anche il caso di un anello, basta prendere un altezza del cilindro molto piccola.