Equazioni con modulo (valore assoluto)
Un’equazione con modulo, come dice il suo nome, è un’equazione in cui appaiono uno o più moduli.
Esempi di equazioni con modulo sono i seguenti:
• ∣x+4∣=3
• 3−2∣x∣=0
• ∣x+4∣=∣x+3∣+x
Non sono invece equazioni con modulo le seguenti:
• x+4=18x+3 - perché non appare alcun modulo
• 3x+∣2∣=0 - perché, non essendoci alcun incognita dentro il modulo, possiamo ricondurla direttamente ad una semplice equazione senza moduli (in questo caso a 3x+2=0 )
Equazioni con un solo modulo
Iniziamo parlando delle equazioni in cui compare un solo modulo. Nella forma più generale esse si presentono nella seguente forma:
∣A(x)∣=B(x) Dove A(x) e B(x) sono funzioni di x .
Modulo e una constante
Iniziamo considerando un caso particolare che risulta più semplice del caso generale: guardiamo cosa succede quando B(x) è una costante.
Chiamiamo questa costante k.
Avremo quindi:
∣A(x)∣=k Dobbiamo distinguere due casi: se k è negativo o positivo.
Il primo caso è il più semplice perché siccome il valore assoluto di qualcosa è sempre positivo, è impossibile che sia uguale a qualcosa di negativo.
Quindi se k<0 l’equazione è impossibile.
Se invece k è positivo basta mettere un ± davanti a k per togliere il modulo. Questo perché siccome k non varia a seconda di x , per avere l’equazione verificata dobbiamo avere:
A(x)=k
Oppure:
A(x)=−k
Che possiamo sintetizzare in:
A(x)=±k Quindi per risolvere questa tipologie di equazioni con modulo dobbiamo risolvere le due equazioni che abbiamo trovato e prendere tutte le soluzioni.
Facciamo un esempio:
• ∣x+4∣=3
Dobbiamo risolvere le due equazioni.
Cominciamo risolvendo la prima:
x+4=3
x=−1
Passiamo alla seconda:
x+4=−3
x=−7
Quindi le soluzioni dell’equazione con modulo saranno 3 e −7 .
Tutto qua, i calcoli potrebbero essere più complicati, ma il procedimento è questo. Se invece abbiamo un’equazione tipo:
∣x5+2∣=−2
Sappiamo subito che è impossibile, perché qualunque sia l’argomento del modulo (cioè quello che sta dentro al modulo), la parte a sinistra dell’uguale sarà positiva e non potrà mai e poi mai essere uguale a −2.
Modulo e una variabile
Passiamo al caso generale:
Abbiamo detto che in generale un’equazione con un modulo appare nella seguente forma:
∣A(x)∣=B(x) Quindi vediamo che risolverle quando B(x) non è costante.
Per fare ciò dividiamo il problema in due casi, quando A(x) è maggiore o uguale a 0 e quando A(x) è minore di 0 .
Trovate le soluzioni dei due casi ci basterà unirle per trovare la soluzione dell’equazione con modulo.
Partiamo dal primo caso:
Se A(x) è maggiore o uguale a 0 abbiamo:
∣A(x)∣=A(x)
Quindi sostituendo:
A(x)=B(x)
Risolvendo otteniamo le soluzioni. Notiamo che non dobbiamo preoccuparci di B(x), perché se B(x)=A(x) e A(x) è positivo anch’esso deve esserlo.
Quindi otteniamo il sistema:
{A(x)≥0A(x)=B(x)
Guardiamo ora invece a quando A(x) è negativo. Se A(x)<0, abbiamo:
∣A(x)∣=−A(x)
Sostituendo:
−A(x)=B(x)
Notiamo che anche questa volta non ci sono problemi sul segno di B(x), perché se A(x) è negativo, allora −A(x) è positivo e quindi l’equazione precedente ci assicura che anche B(x) lo sarà.
Quindi otteniamo il sistema:
{A(x)<0−A(x)=B(x)
Unendo i due sistemi otteniamo le soluzioni dell’equazione con modulo.
Quindi dobbiamo unire le soluzioni dei sistemi, ovvero:
{A(x)≥0A(x)=B(x)∪{A(x)<0−A(x)=B(x) Con questa formula potrete risolvere qualsiasi equazione con un modulo!
Equazioni con due o più moduli
Vediamo ora come risolvere equazioni dove compaiono 2 o più moduli.
Ecco alcuni esempi:
• ∣2x+1∣−4x+∣x∣=9
• ∣3−2x∣−5x=∣3x−1∣
• ∣x2−x−3∣+4x−∣x∣=0
Per risolvere questo tipo di equazioni bisogna studiare il segno dell'argomento di ogni modulo singolarmente e poi trovare le possibili soluzioni per i vari casi.
Prendiamo come esempio la prima equazione riportata sopra:
∣2x+1∣−4x+∣x∣=9
In questa equazione sono presenti 2 moduli, iniziamo studiando il primo modulo:
∣2x+1∣
Sappiamo che il modulo sarà sempre positivo, ma ci serve di conoscere il segno dell'argomento per capire se cambierà segno:
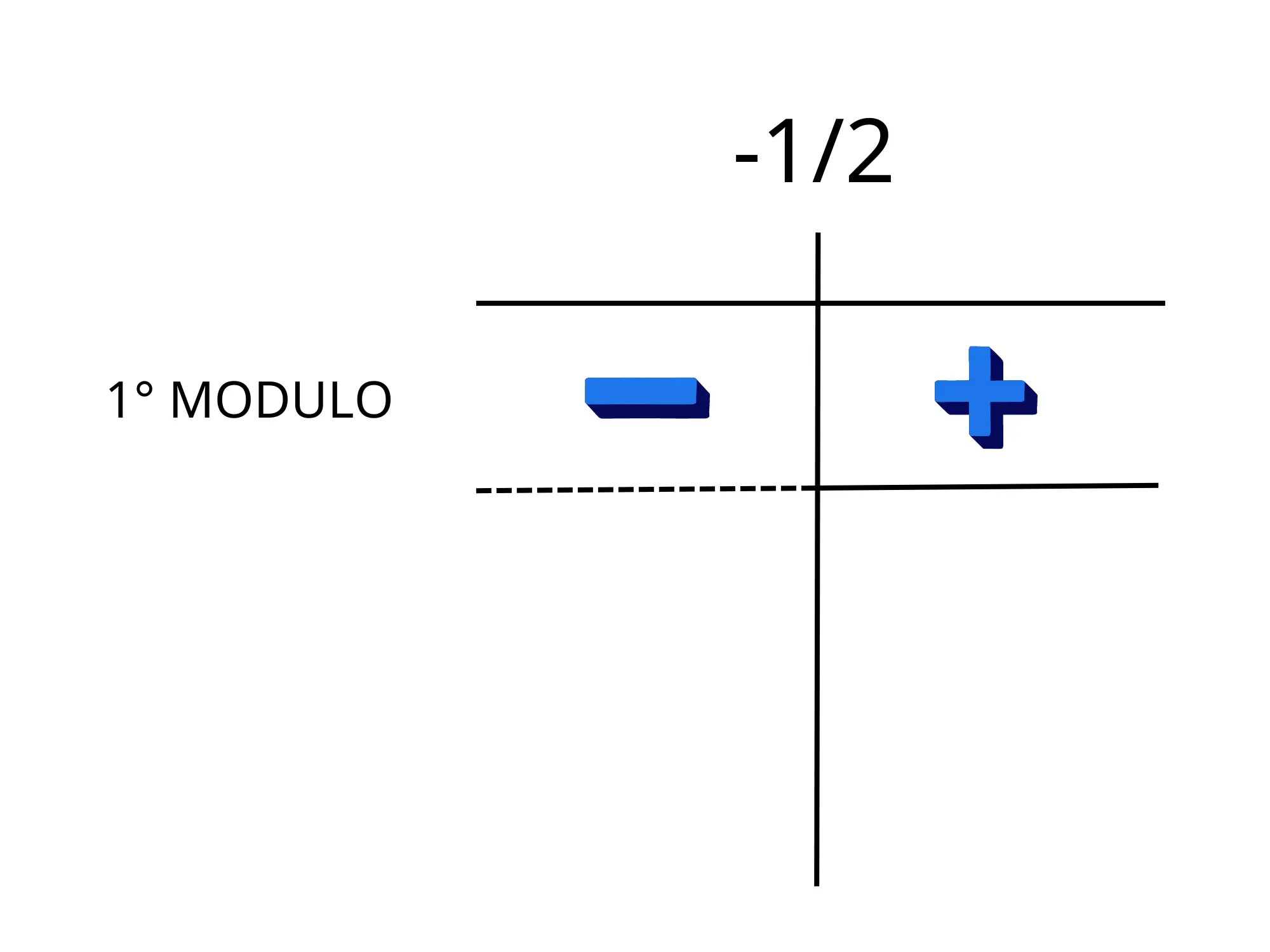
2x+1>0⟶x>−21
Ora sappiamo che per le x minori di −21 l’espressione all’interno del modulo sarà negativa e quindi il modulo cambierà segno all'argomento per renderla positiva.
Se x≥−21:
∣2x+1∣=2x+1
Se x<−21:
∣2x+1∣=−(2x+1)= −2x−1
Ci annotiamo i risultati nel seguente grafico dei segni e procediamo nello studio del prossimo modulo.
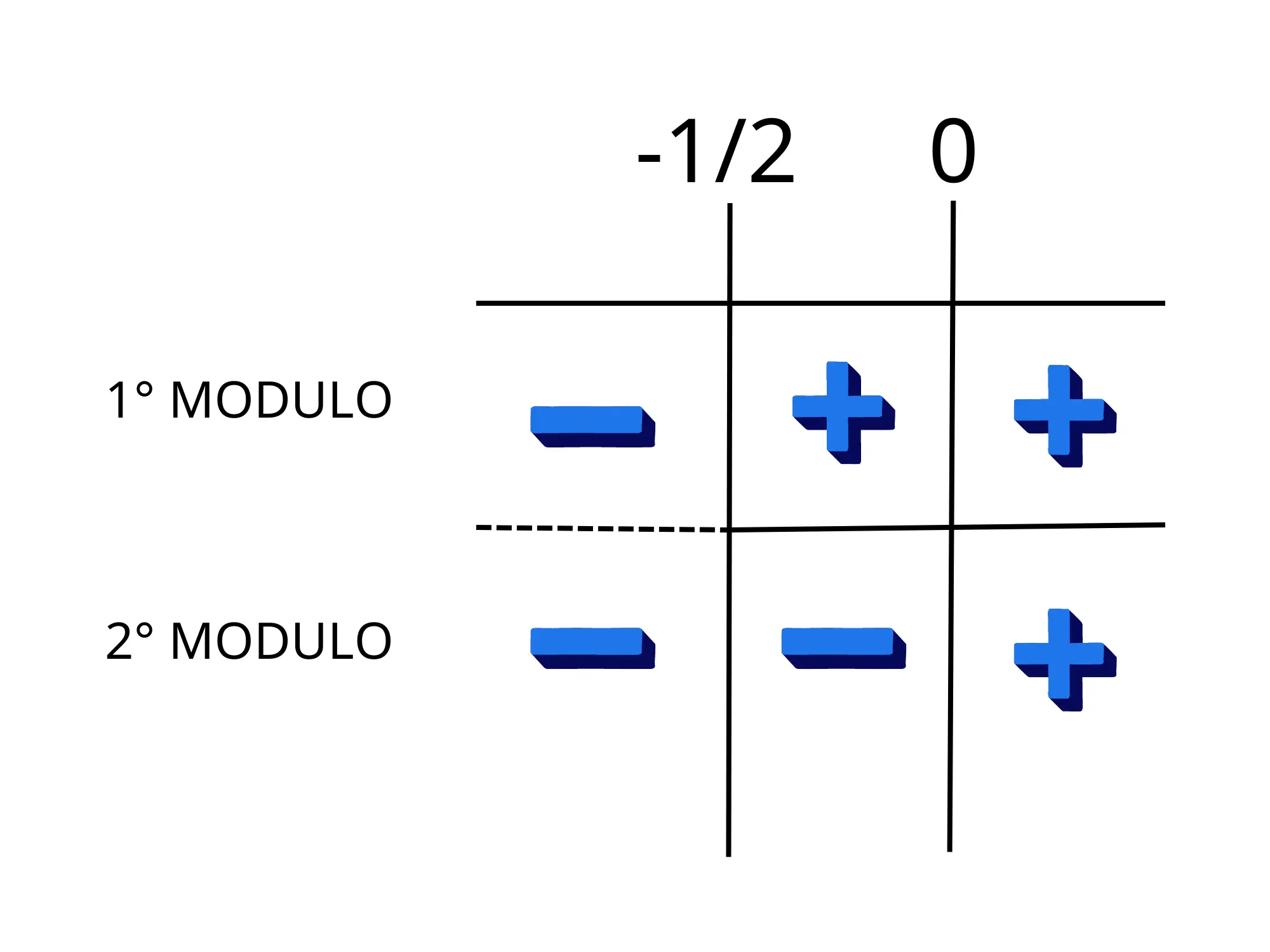
Il modulo successivo è ∣x∣ in questo caso sarà facile capire che si annulla per x=0 e di conseguenza:
Se x≥0:
∣x∣=x
Se x<0:
∣x∣=−x
Lo scriviamo nel grafico dei segni e procediamo con la risoluzione dell’equazione.
Ora ci basterà leggere il grafico e per ogni situazione scrivere l’equazione corrispondente e fare l’ unione delle soluzioni accettabili di tutte le equazioni.
Se x<−21:
−2x−1−4x−x=9
x=−710 - ACCETTABILE
Se −21≤x<0 :
2x+1−4x−x=9
x=−38 - NON accettabile perché non rispetta la condizione −21≤x<0
Se x≥0:
2x+1−4x+x=9
x=−8 - NON accettabile perché non rispetta la condizione x≥0
L'unica vera soluzione dell’equazione sarà quindi x=−710
Equazioni con moduli dentro altri moduli
Passiamo ora all’ultimo caso che analizzeremo in questa lezione, ovvero quello di uno o più moduli dentro un modulo.
Vediamo alcuni esempi:
• ∣x−∣x2−3∣+2∣=3
• ∣∣3x−1∣+x−∣2x∣+5∣=∣x∣
• 2x−∣∣x−3∣−x∣=8
Per risolvere questo tipo di equazione basta applicare i metodi visti in precedenza uno dopo l’altro.
Le soluzioni potrebbero essere molte, soprattutto se sono presenti tanti moduli.
Prendiamo il secondo esempio, dove è necessario usare due dei metodi visti in precedenza:
∣3x−1∣+x−∣2x∣+5∣=∣x∣
La prima cosa da notare è che entrambi i membri dell’equazione sono moduli e quindi, come prima, avremo che il primo membro è uguale a ± il secondo membro.
Quindi otterremo queste 2 equazioni:
• ∣3x−1∣+x−∣2x∣+5=x
• ∣3x−1∣+x−∣2x∣+5=−x
Ora risolviamole entrambe separatamente con il metodo già visto e troviamo le soluzioni.
Iniziamo dalla prima:
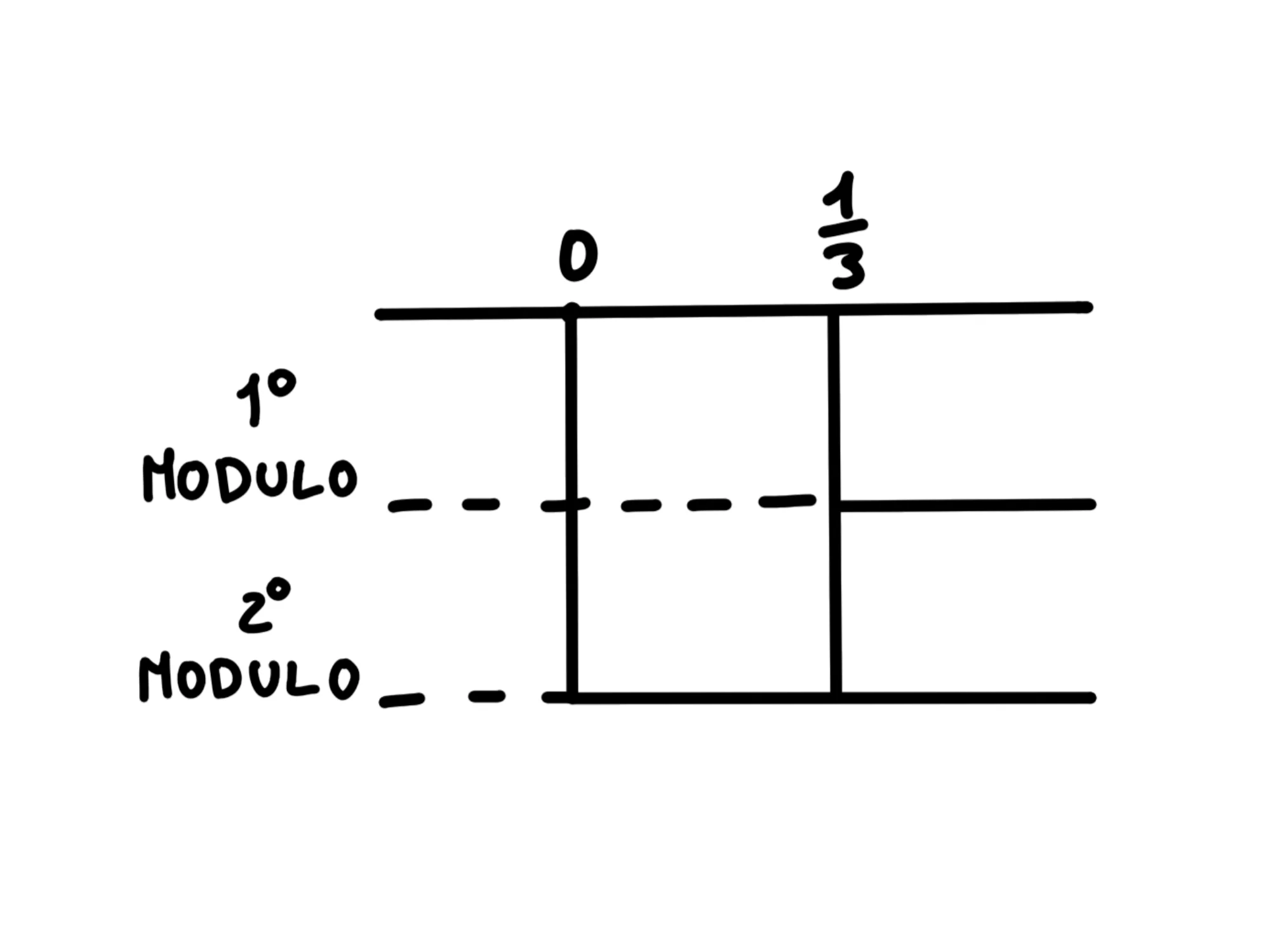
Studiamo il segno degli argomenti dei moduli:
3x−1>0
x>31
Per il secondo modulo abbiamo:
2x>0
x>0
Tracciamo il grafico dei segni dei moduli:
Abbiamo tre casi, ma prima di studiarli singolarmente semplifichiamo l'equazione generale:
∣3x−1∣+x−∣2x∣+5=x ⟶∣3x−1∣−∣2x∣+5=0
Il primo è quando x<0, in tal caso l'equazione diventa:
−(3x−1)−(−2x)+5=0
−3x+1+2x+5=0
−x=−6
x=6
Però non è vero che 6<0, quindi la soluzione NON è accettabile.
Passiamo al secondo caso:
Adesso abbiamo 0≤x<31 e l'equazione diventa:
−(3x−1)−2x+5=0
−3x+1−2x+5=0
−5x+6=0
x=56
Ma 56>31, quindi anche questa soluzione NON è accettabile.
Passiamo al terzo e ultimo caso, cioè quando x≥31:
3x−1−2x+5=0
x=−4
Anche questa soluzione non è accettabile, quindi la prima equazione non ha alcuna soluzione.
Passiamo alla seconda:
Riscriviamola come:
∣3x−1∣+x−∣2x∣+5=−x ⟶∣3x−1∣+2x−∣2x∣+5=0
I moduli degli argomenti solo gli stessi di prima, quindi anche il grafico dei segni sarà uguale:
Studiamo quindi i soliti tre casi:
Se x<0 abbiamo:
−(3x−1)+2x−(−2x)+5=0
−3x+1+2x+2x+5=0
x=−6
Finalmente abbiamo trovato una soluzione ACCETTABILE !
Passiamo ora al secondo caso:
Se 0≤x<31, allora:
−(3x−1)+2x−2x+5=0
−3x+1+5=0
x=2
Siccome 2<31, questa soluzione Non è accettabile.
Infine abbiamo l'ultimissimo caso, quello dove x≥31. Così otteniamo:
3x−1+2x−2x+5=0
3x=−4
x=3−4
Questa soluzione ovviamente non è accettabile perché 3−4<31.
Quindi l'unica soluzione dell'equazione iniziale è −6.