Frazioni

Cos'è una frazione?

Per spiegare cosa sia una frazione, raccontiamo una storiella comunemente usata:

È il compleanno di un vostro amico. Avete giocato per ore ed adesso è arrivato il momento di soffiare le candeline. Il vostro amico soffia e voi applaudite e gli fate gli auguri. Ora volete mangiare la torta. La torta però è solo una, non potete dare un'intera torta a testa.

Come fate allora? Tagliate la torta. Cioè la dividete in parti più piccole per darne una ad ognuno.

Poniamo che oltre a te e al festeggiato ci siano altri due vostri amici. Se volete che ognuno di voi quattro mangi la stessa quantità di torta, dovete dividerla in quattro parti uguali, come nella figura:

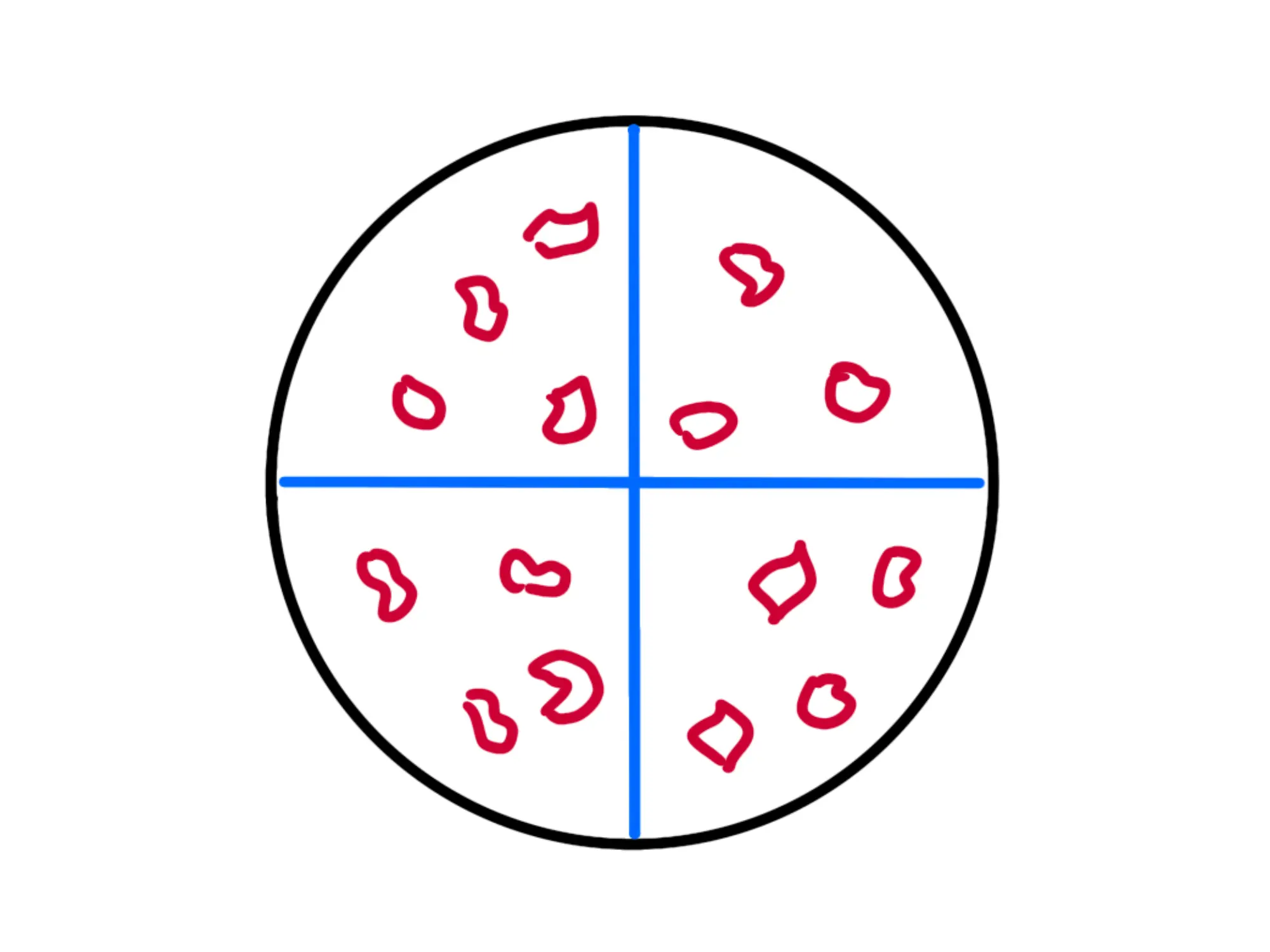
Ognuno di voi ora non ha un'intera torta, ma solo un pezzo. Avete solo un quarto della torta. Cioè avete diviso $\displaystyle { 1 }$ per $\displaystyle { 4 }$ .

Però non usiamo la notazione con i due punti, ma mettiamo il numero che stiamo dividendo, sotto di esso disegniamo una lineetta e sotto ancora scriviamo il numero di parti in cui lo abbiamo diviso. Quindi ognuno di voi avrà $\displaystyle { {1\over 4} }$ della torta.

Se invece eravate in $\displaystyle { 5, }$ avrete diviso la torta in $\displaystyle { 5 }$ parti uguali, come nella figura:

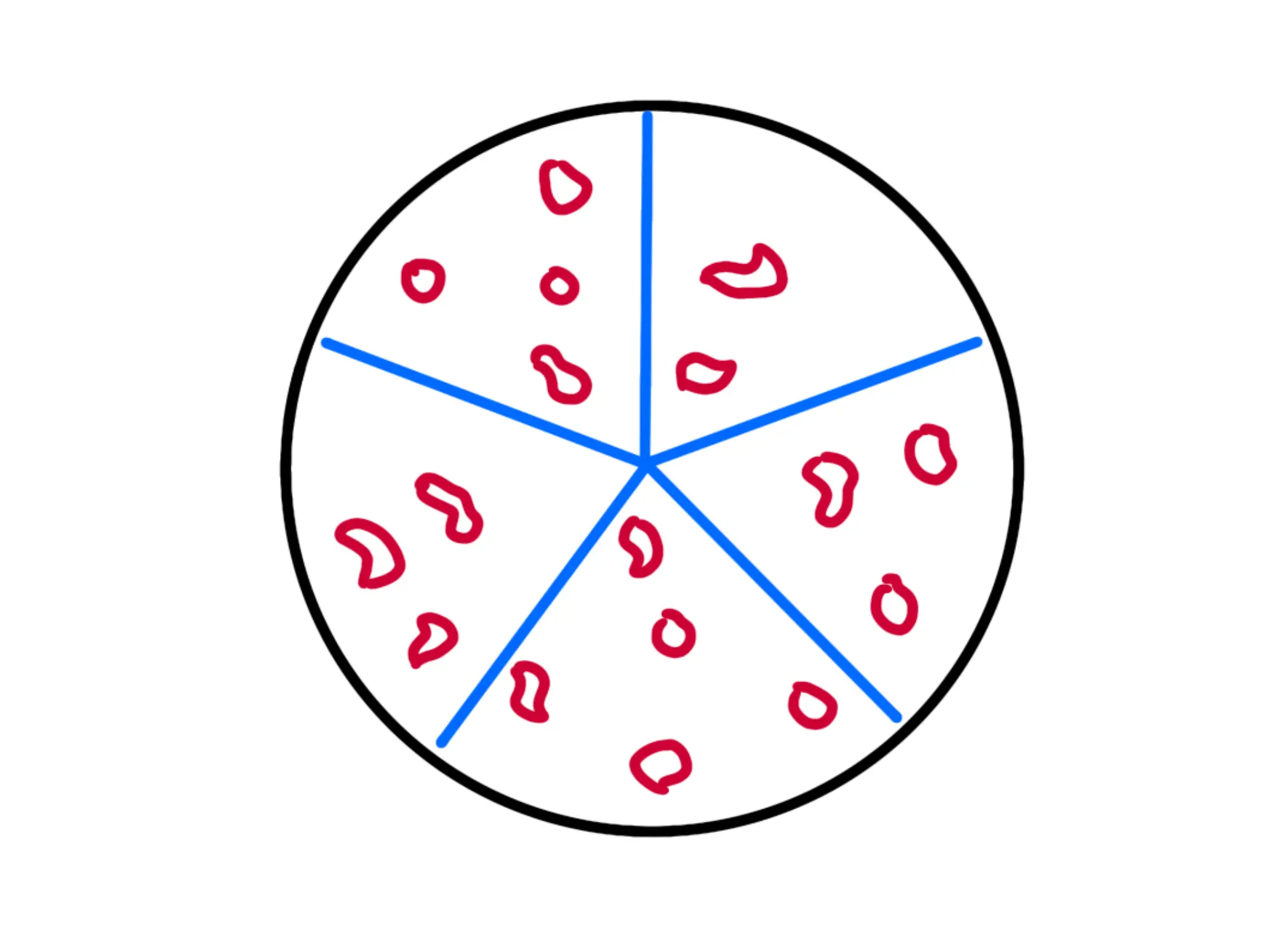
Quindi ognuno di voi avrebbe avuto $\displaystyle { {1\over 5} }$ della torta.

Poniamo che scopriate solo dopo aver tagliato la torta che uno dei vostri amici è intollerante al lattosio. Non può dunque mangiare la torta, quindi decidete di dare la fetta extra al festeggiato.

Adesso quindi lui non avrà più solo $\displaystyle { {1\over 5} }$ della torta, ma, avendo $\displaystyle { 2 }$ fette, avrà $\displaystyle { {2\over 5} }$ della torta. I suoi pezzetti sono evidenziati nella seguente figura.

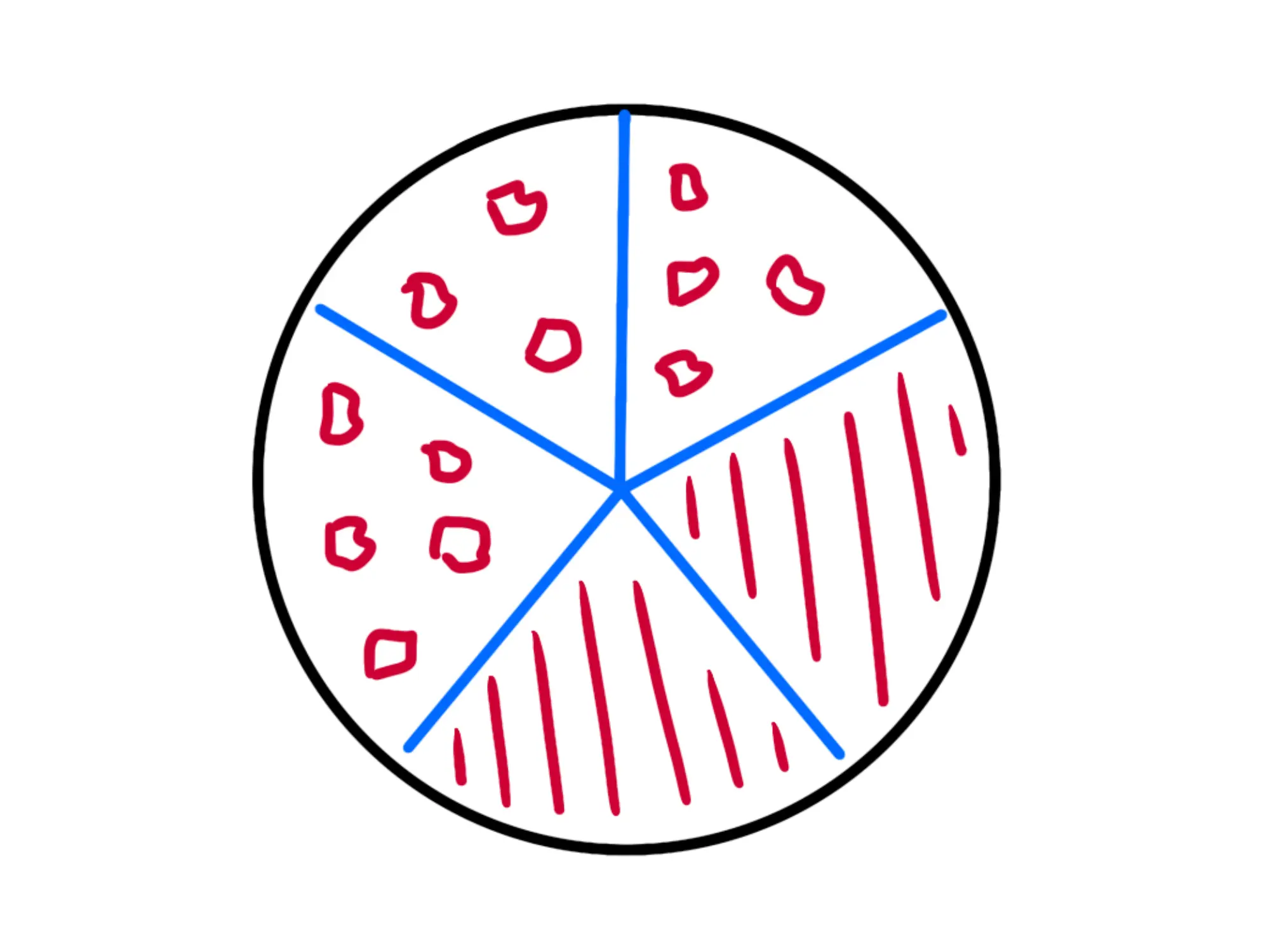
Quindi, per indicare una frazione, dovete mettere il numero di parti che avete, poi mettete un trattino e infine il numero di parti in cui è stata divisa.

Proponiamo di seguito qualche altro esempio per chiarire il concetto.

Se taglio una mela in $\displaystyle { 4 }$ spicchi ma ne mangio solo $\displaystyle { 3, }$ allora ho mangiato $\displaystyle { 3\over 4 }$ della mela.

Se ci sono $\displaystyle { 10 }$ cioccolatini sul tavolo e ne prendo $\displaystyle { 3, }$ ho preso $\displaystyle { 3\over 10 }$ del numero di cioccolatini.

Diamo ora dei nomi alle varie parti di una frazione:

Il numero che sta sopra il trattino (cioè il numero di parti che ho) è detto numeratore.

Quello che invece si trova sotto (cioè il numero di parti in cui ho diviso l'$\displaystyle { 1 }$ ) si chiama denominatore.

Il trattino ha un nome specifico: si chiama linea di frazione.

Nella frazione $\displaystyle { {5\over 7}, }$ dunque, il numeratore è $\displaystyle { 5 }$ e il denominatore è $\displaystyle { 7. }$

Ora notiamo una cosa interessante: se prendo una pizza e la taglio in $\displaystyle { 10 }$ fette e ne prendo $\displaystyle { 5, }$ avrò preso $\displaystyle { 5\over 10 }$ della pizza. Ma se guardiamo la figura qui sotto, notiamo che abbiamo preso esattamente metà pizza:

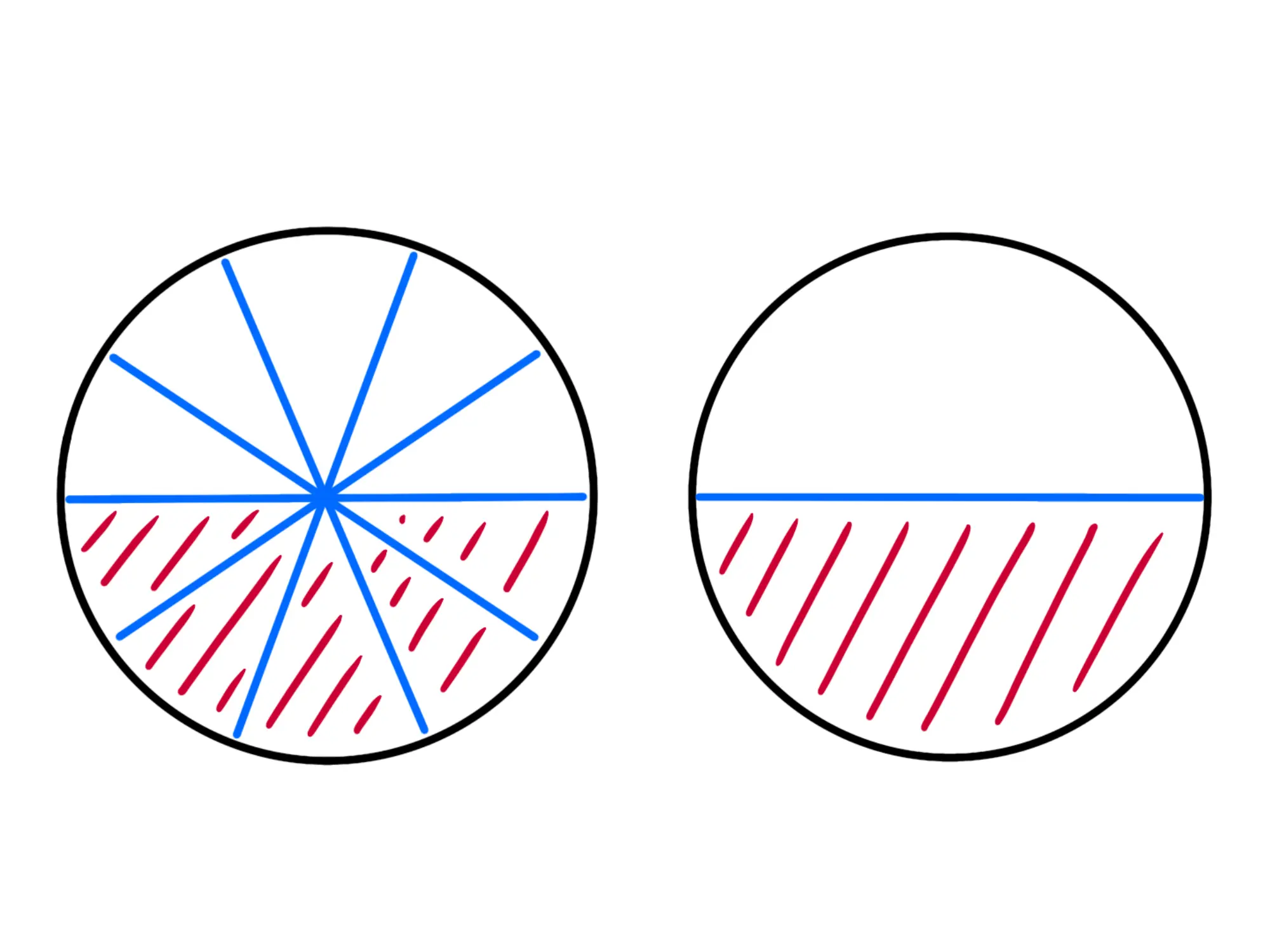
Quindi alcune frazioni sono uguali? Proprio così. Se io moltiplico o divido il numeratore e il denominatore di una stessa frazione per uno stesso numero, la frazione rimane la stessa, non cambia.

Infatti, se prendo $\displaystyle { {5\over 10} }$ e divido il numeratore e il denominatore per $\displaystyle { 5, }$ ottengo proprio $\displaystyle { {1\over 2}. }$

Come fa a funzionare? Questo succede perché se io aumento il numeratore, prendo più parti, ma se aumento il denominatore rendo ogni parte più piccola e quindi si compensano a vicenda.

Ricordate però che potete solo moltiplicare o dividere, se sommate o sottraete cambiate la frazione.

Ricordandoci che una frazione non è altro che una divisione tra il numeratore e il denominatore, quello che abbiamo fatto è semplicemente stato applicare la proprietà invariantiva della divisione.

Vediamo ora le differenze tra frazioni proprie, frazioni improprie e frazioni apparenti.

Le frazioni proprie sono come gli esempi che abbiamo visto finora, dove il numeratore è più piccolo del denominatore.

Se invece il numeratore è più grande del denominatore, allora si dice che la frazione è impropria.

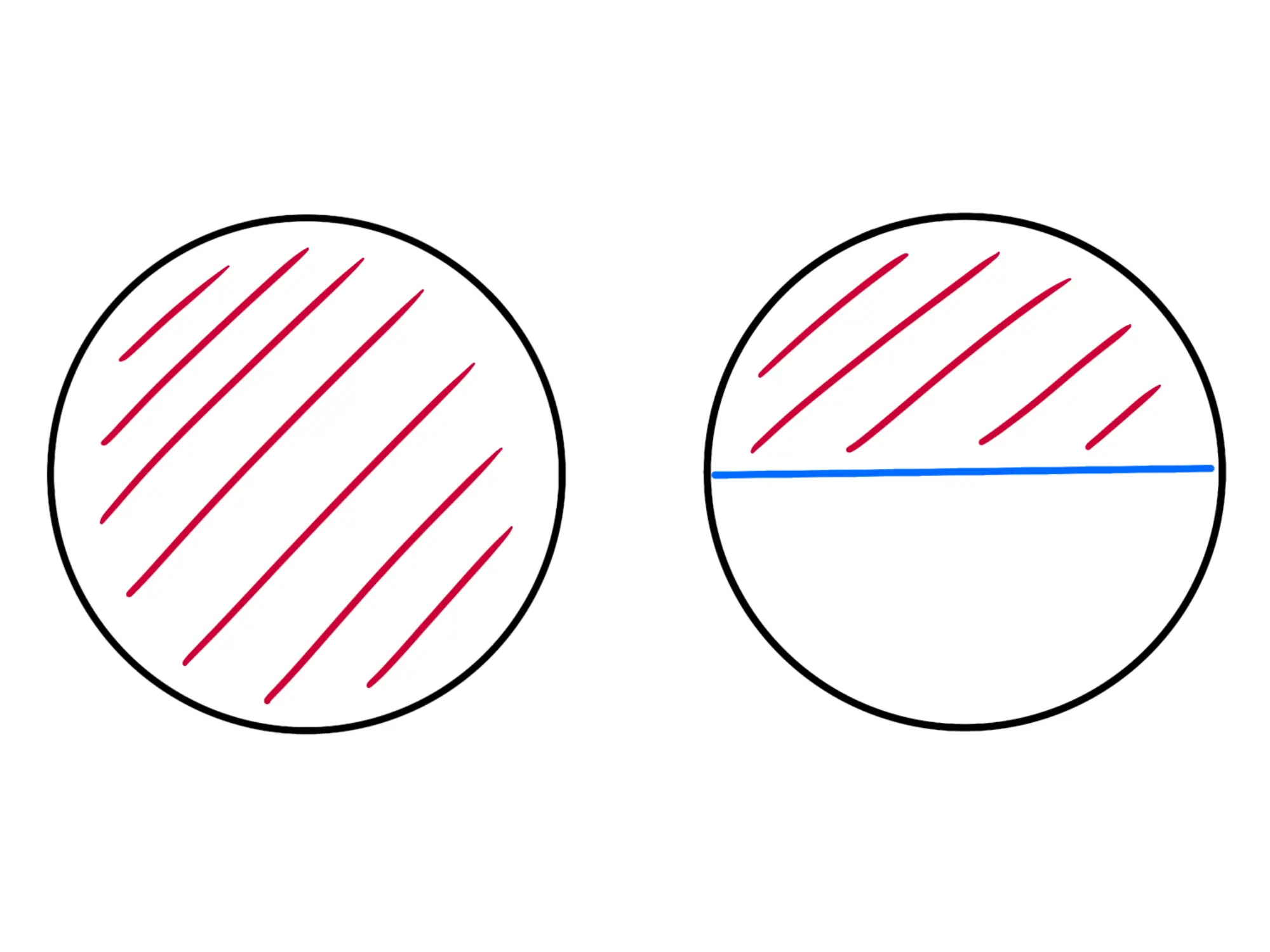
Che significa? Significa che io ho un'intero più qualche altro pezzetto. Per esempio, se ho $\displaystyle { {3\over 2} }$ pizze, significa che ho una pizza intera più mezza pizza:

Mentre si dice frazione apparente una frazione in cui il numeratore è un multiplo del denominatore.

Perché sono chiamate apparenti? Perché appaiono, cioè sembrano, delle frazioni, ma in realtà sono numeri interi.

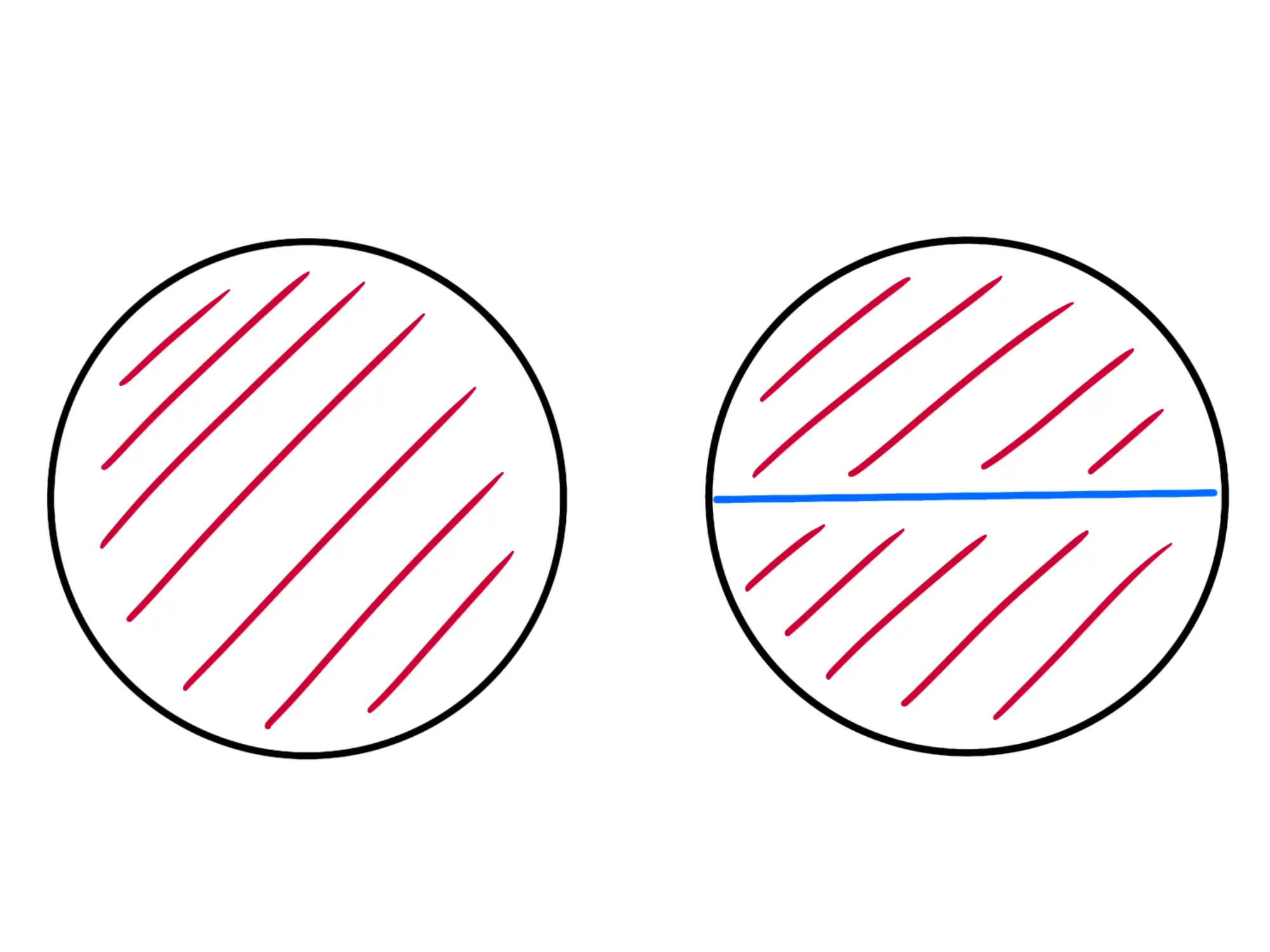
Se infatti ho $\displaystyle { {4\over 2} }$ pizze, siccome posso dividere numeratore e denominatore per $\displaystyle { 2, }$ è la stessa cosa di avere $\displaystyle { 2\over 1 }$ pizze, cioè $\displaystyle { 2 }$ pizze. Quindi sì, ho diviso le pizze in più parti, ma ce l'ho tutte io:

Infine, il reciproco di una frazione è la frazione capovolta. Cioè scambio il numeratore con il denominatore.

Quindi il reciproco di $\displaystyle { {2\over 3} }$ è $\displaystyle { {3\over 2}, }$ mentre quello di $\displaystyle { {7\over 12} }$ è $\displaystyle { {12\over 7}. }$ Ricordatevi del reciproco perché ci servirà per fare la divisione fra frazioni tra poco.

Vediamo ora come si fanno le operazioni con le frazioni:

Operazioni con frazioni

Come abbiamo visto prima, se un vostro amico non poteva mangiare più la torta e davate due fette al vostro amico, egli aveva $\displaystyle { 2\over 5 }$ della torta.

Questo vuol dire che se prendo $\displaystyle { 1\over 5 }$ e gli sommo $\displaystyle { 1\over 5 }$ ottengo $\displaystyle { {2\over 5}, }$ cioè:

$\displaystyle { {1\over 5}+ {1\over 5} = {2\over 5 } }$

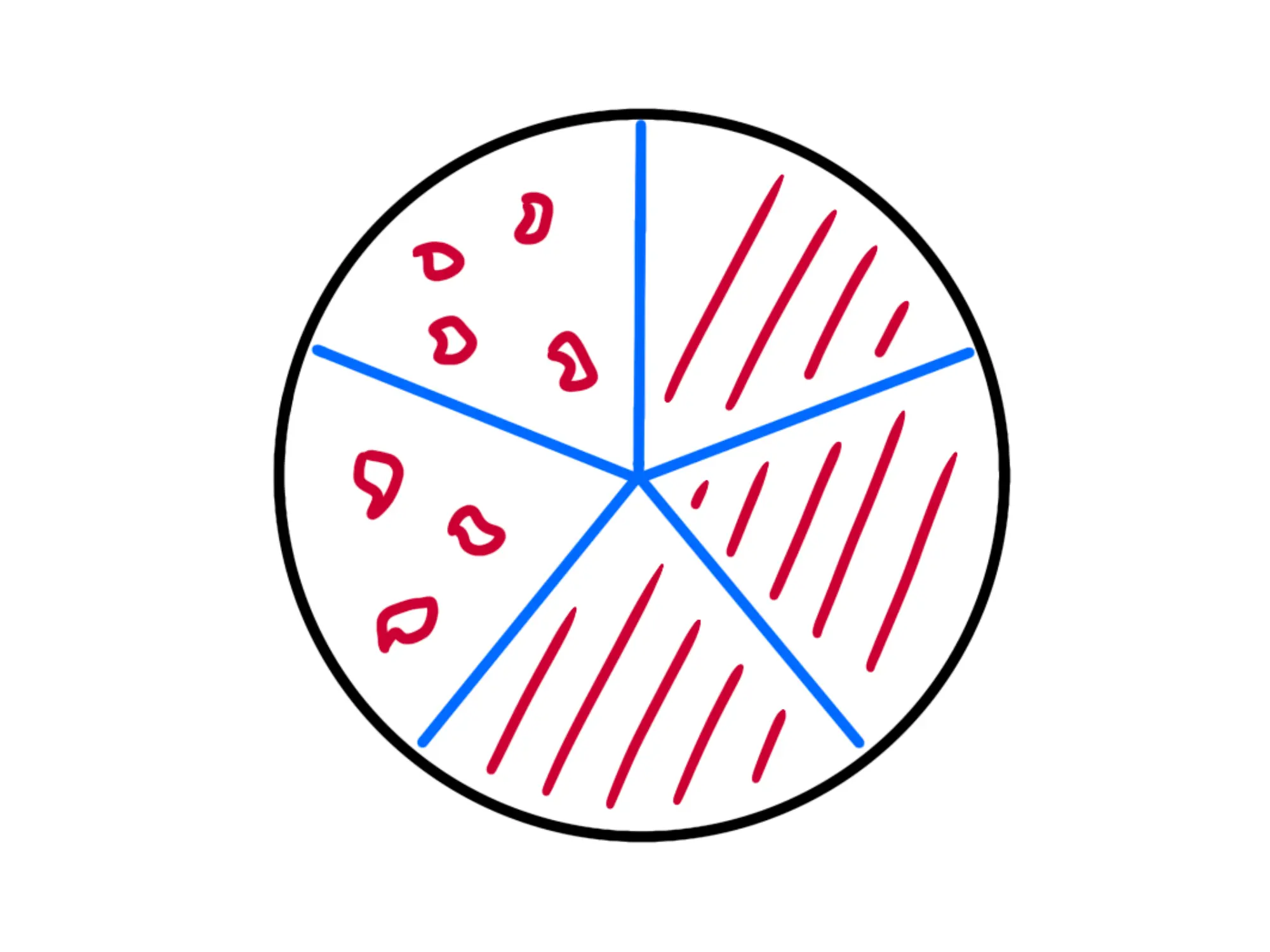
Poniamo adesso che un vostro amico debba tornare di corsa a casa e che dunque non mangi la sua fetta. Tu non la vuoi e nemmeno l'altro vostro amico la vuole, dunque date anche quest'altra al festeggiato. Ora lui ha $\displaystyle { 3 }$ fette della torta e, come si vede nella figura qui sotto, avrà $\displaystyle { {3\over 5} }$ della torta:

Quindi prima aveva $\displaystyle { {2\over 5}, }$ gli abbiamo sommato $\displaystyle { {1\over 5} }$ ed abbiamo ottenuto $\displaystyle { {3\over 5}: }$

$\displaystyle { {2\over 5}+ {1\over 5} = {3\over 5} }$

Ma quindi per sommare frazioni con lo stesso denominatore bisogna solo sommare i numeratori? Eh già, è proprio così! Quindi, se devo fare, per esempio, $\displaystyle { {3\over7} + {2\over 7}, }$ farà $\displaystyle { {5\over 7}, }$ facile no?

Vediamo qualche altro esempio di somma delle frazioni con lo stesso denominatore:

• $\displaystyle { {4\over 7} + {2\over 7} = {6\over 7} }$

• $\displaystyle { {1\over 3} + {1\over 3} = {2\over 3} }$

• $\displaystyle { {2\over 10} + {5\over 10} = {7\over 10} }$

Però potrebbe succedere che volete sommare due frazioni che non hanno lo stesso denominatore. Là le cose si fanno più complicate, ma tranquilli, ora vi spiegheremo come fare:

Poniamo di voler calcolare quanto fa $\displaystyle { {1\over 6} + {1\over 9}. }$ Come fare?

Arrivati a questo punto dobbiamo ragionare: noi, finora, cosa sappiamo fare? Sappiamo sommare due frazioni che hanno lo stesso denominatore. Come posso ricondurre il mio problema al caso che già conosco?

Noi sappiamo pure che moltiplicare numeratore e denominatore di una frazione per uno stesso numero non cambia niente. Allora potrei usare questo fatto per portare le frazioni allo stesso denominatore e poi sommarle!

Vediamo più dettagliatamente cosa intendo:

Io prendo $\displaystyle { {1\over 9}, }$ e so che posso moltiplicare il numeratore e il denominatore per $\displaystyle { 2 }$ senza cambiare la frazione. Dunque devo avere:

$\displaystyle { {1\over 9} = {2\over 18} }$

Poi prendo $\displaystyle { {1\over 6} }$ e moltiplico il numeratore e il denominatore per $\displaystyle { 3, }$ scoprendo che:

$\displaystyle { {1\over 6} = {3\over 18} }$

Quindi, per fare $\displaystyle { {1\over 6} + {1\over 9}, }$ posso scrivere $\displaystyle { {3\over 18} }$ al posto di $\displaystyle { {1\over 6} }$ e scrivere $\displaystyle { {2\over 18} }$ al posto di $\displaystyle { {1\over 9}. }$ Così facendo scopro che:

$\displaystyle { {1\over 6} + {1\over 9} = {3\over 18} + {2\over 18} }$

Ed ora ho due frazioni con lo stesso denominatore che so come sommare! Quindi il risultato sarà $\displaystyle { {5\over 18}. }$

Ok, però potreste obbiettare che quel $\displaystyle { 3 }$ e quel $\displaystyle { 2 }$ per cui ho moltiplicato li ho tirati fuori dal niente, non vi ho spiegato perché usando quelli funziona.

Come ho fatto a scoprire che erano quelli i due numeri? Dovete notare che il denominatore a cui vogliamo arrivare è il minimo comune multiplo dei denominatori delle due frazioni (infatti $\displaystyle { mcm(6,9) = 18 }$ ).

Una volta trovato, ti basta trovare per quale numero devi moltiplicare il denominatore per arrivarci. Quindi nel caso di $\displaystyle { {1\over 6}, }$ devo notare che $\displaystyle { 6\times 3 = 18 }$ e dunque moltiplicherò per $\displaystyle { 3, }$ mentre nel caso di $\displaystyle { {1\over 9} }$ noto che $\displaystyle { 9\times 2 = 18, }$ dunque è $\displaystyle { 2 }$ il nostro numero.

Se non riuscite a trovare ad occhio il numero per cui moltiplicare, potete dividere l'mcm per il denominatore per trovarlo ( $\displaystyle { 18:6 =3 }$ e $\displaystyle { 18:9 = 2 }$ ).

Vediamo qualche altro esempio: calcoliamo $\displaystyle { {1\over 7} + {1\over 5}. }$

L'mcm di $\displaystyle { 7 }$ e $\displaystyle { 5 }$ è $\displaystyle { 35 }$ . Quindi otterrò:

$\displaystyle { {1\over 7} + {1\over 5} = {5\over 35} + {7\over 35} = {12\over 35} }$

Se invece voglio fare $\displaystyle { {1\over 4} + {1\over 2}, }$ noto che l'mcm è $\displaystyle { 4 }$ ed ottengo:

$\displaystyle { {1\over 4} + {1\over 2} = {1\over 4} + {2\over 4} = {3\over 4} }$

Se invece di sommare sto sottraendo, il procedimento è lo stesso, solo che alla fine invece di sommare i due numeratori, li sottrarò. Quindi, ad esempio, se voglio calcolare $\displaystyle { {1\over 2} - {1\over 3}, }$ otterrò:

$\displaystyle { {1\over 2} - {1\over 3} = {3\over 6} - {2\over 6} = {1\over 6} }$

Ora siamo pronti per studiare la moltiplicazione tra frazioni:

Poniamo di aver diviso una pizza in tre fette e noi prendiamo solo una fetta:

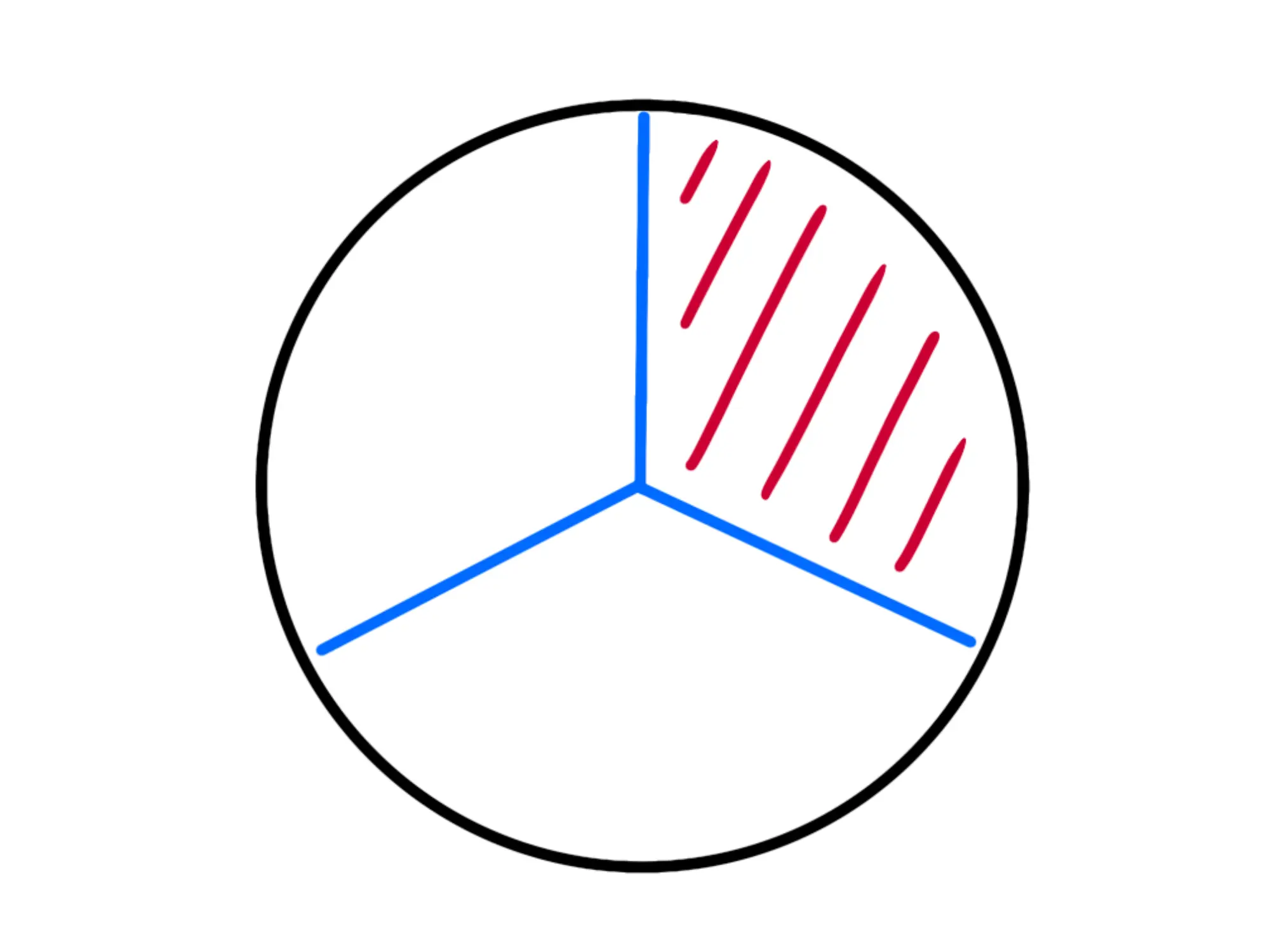
Avremo $\displaystyle { {1\over 3} }$ della pizza.

Adesso, prendiamo solo $\displaystyle { {1\over 3} }$ della nostra fetta. Per farlo la dividiamo in tre parti uguali e ne prendiamo solo una:

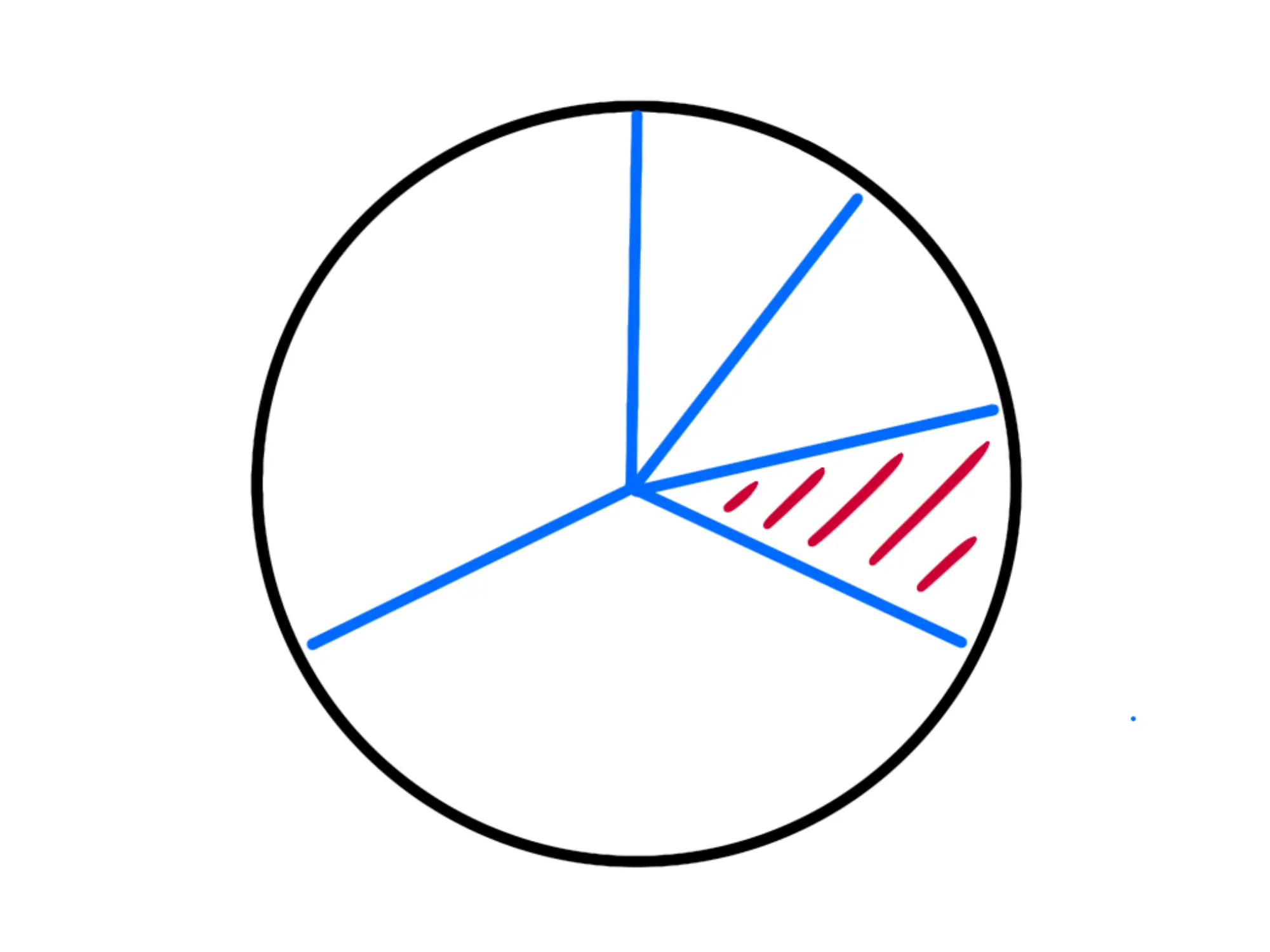
Se dividiamo pure le altre fette in tre, notiamo facilmente che quello che ci rimane è solo $\displaystyle { {1\over 9} }$ della pizza:

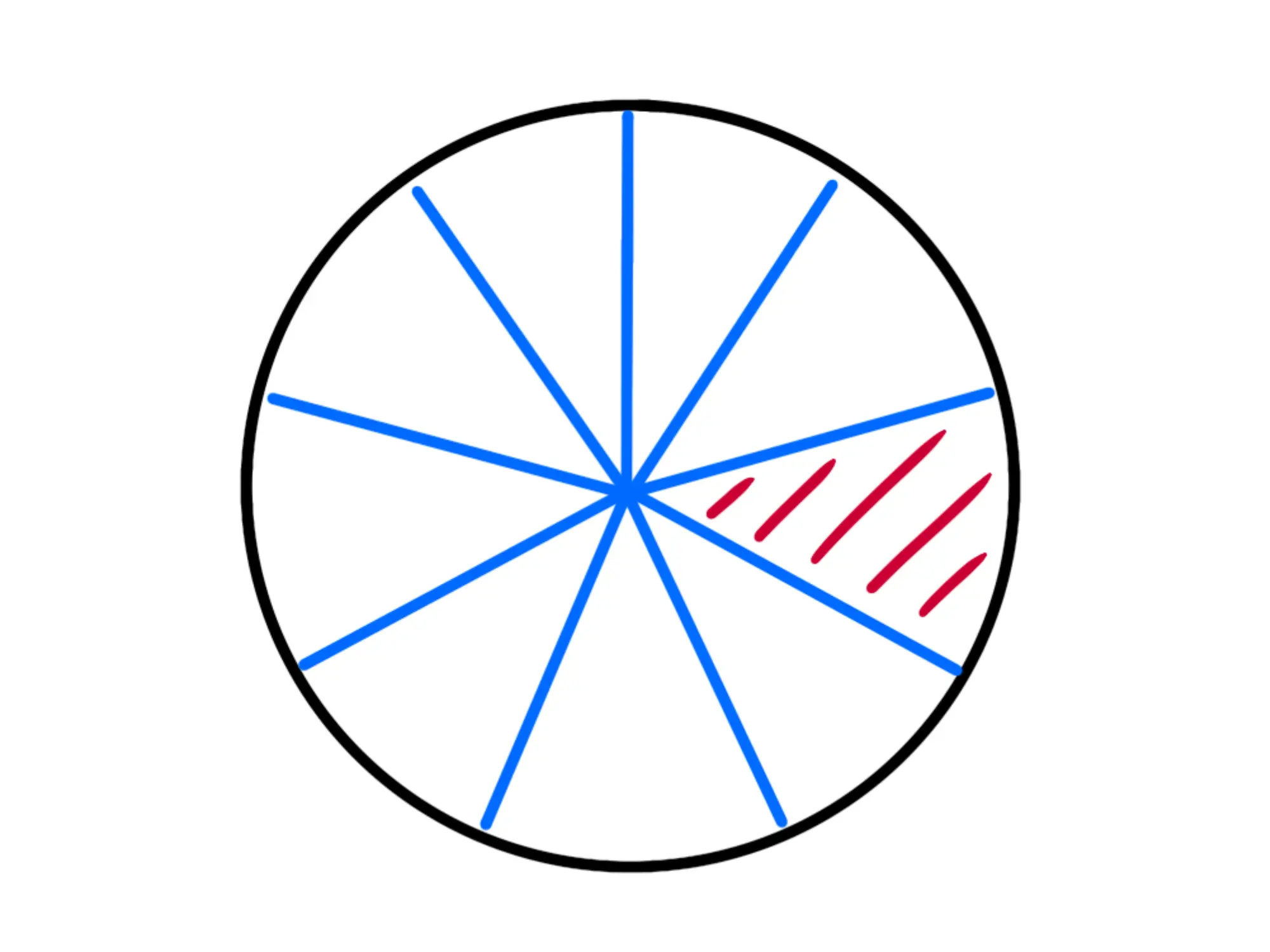
Dunque abbiamo preso $\displaystyle { {1\over 3} }$ di $\displaystyle { {1\over 3}, }$ cioè abbiamo fatto $\displaystyle { {1\over 3}\times {1\over 3} }$ ed abbiamo ottenuto $\displaystyle { {1\over 9}. }$ Cioè:

$\displaystyle { {1\over 3}\times {1\over 3} = {1\over 9} }$

Se torniamo a quando avevamo un terzo della pizza e questa volta prendiamo $\displaystyle { {2\over 3} }$ della nostra fetta, cioè la dividiamo in tre parti e ne prendiamo due, notiamo facilmente che avremo $\displaystyle { {2\over 9} }$ della pizza:

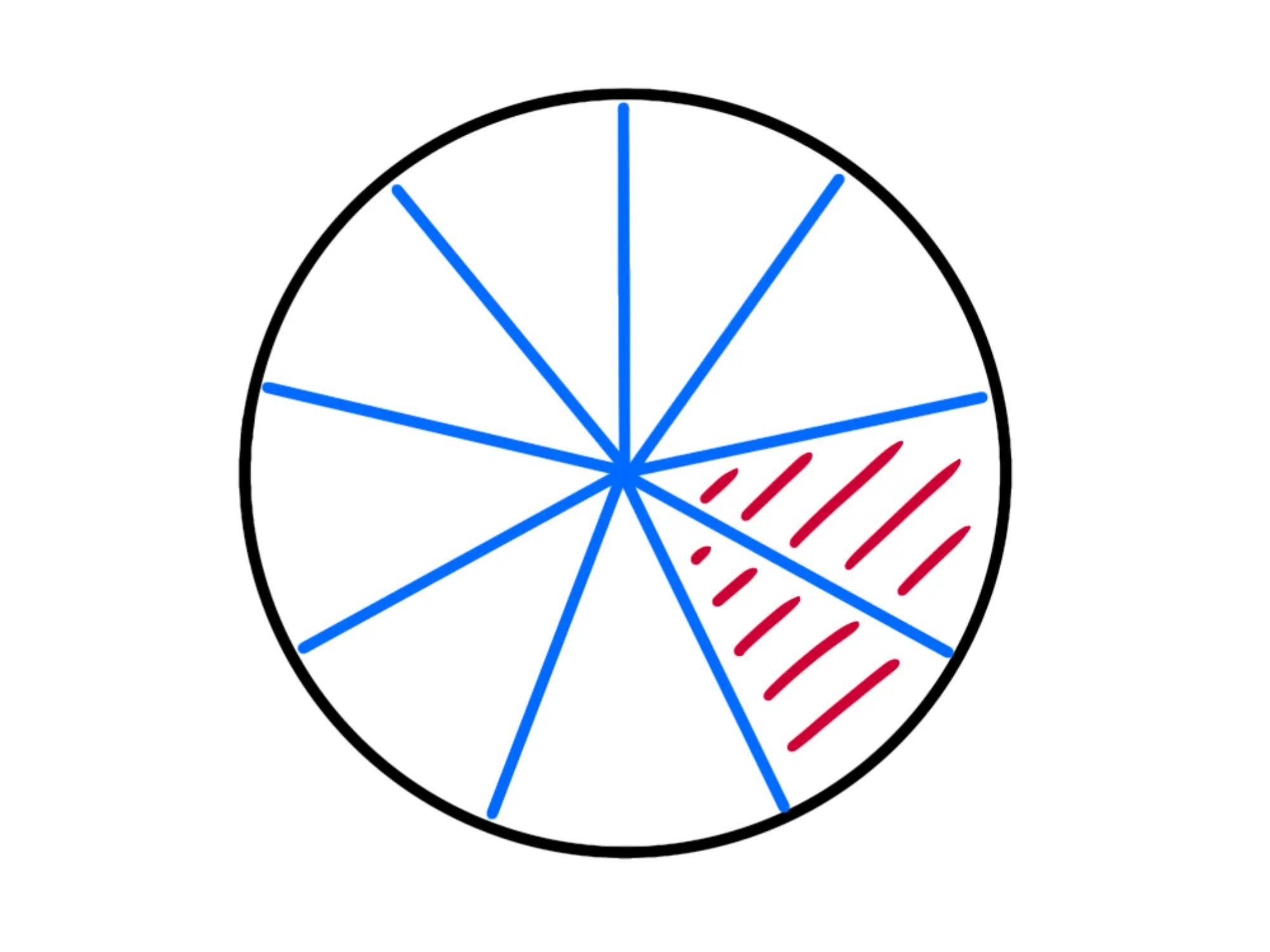
Quindi abbiamo ottenuto che:

$\displaystyle { {1\over 3}\times {2\over 3} = {2\over 9} }$

Ma quindi basta moltiplicare i due denominatori e i due numeratori? Sì, è proprio così!

Quindi se ho $\displaystyle { {2\over 7}\times {3\over 5} }$ il risultato sarà $\displaystyle { {6\over 35}. }$

Ecco di seguito qualche altro esempio:

• $\displaystyle { {1\over 2}\times {3\over 4} = {3\over 8} }$

• $\displaystyle { {5\over 9} \times {2\over 3} = {10\over 27} }$

• $\displaystyle { {13\over 2}\times {3\over 11} = {39\over 22} }$

Ok, però c'è un trucchetto fondamentale da imparare! Quando avete moltiplicazioni fra frazioni, nella maggior parte dei casi, potete semplificare alcune cose. In questo modo i numeri diventeranno molto più piccoli e sarà più facile fare i calcoli:

Innanzitutto, prima di moltiplicare, riducete le frazioni ai minimi termini. Che significa?

Una frazione è detta ridotta ai minimi termini se il numeratore e il denominatore non hanno nessun divisore in comune (tranne $\displaystyle { 1, }$ che divide tutti i numeri).

Quindi, $\displaystyle { {2\over 3} }$ è ridotta ai minimi termini, mentre $\displaystyle { {4\over 8} }$ non lo è, perché sono entrambi divisibili per $\displaystyle { 4. }$

Per ridurla ai minimi termini, devo sfruttare il fatto che posso dividere il numeratore e il denominatore per uno stesso numero, che in questo caso sarà proprio il loro divisore comune.

Quindi $\displaystyle { {4\over 8}, }$ dividendo numeratore e denominatore per $\displaystyle { 4, }$ la trasformo in $\displaystyle { {1\over 2} }$ che adesso è ridotto ai minimi termini.

Riducendo le frazioni rendo i numeri con cui lavoro molto più piccoli.

Ma non è finita qui! C'è un altro trucchetto utilissimo: quando moltiplico due frazioni, possso semplificare lungo le linee della $\displaystyle { \times . }$

Che significa? Tranquilli, può suonare complicato ma è semplice, ora vedrete un esempio e lo capirete subito:

Calcoliamo $\displaystyle { {2\over 3} \times {9\over 16}. }$ Le frazioni sono ridotte ai minimi termini, ma ancora non ci conviene moltiplichiamo perché possiamo semplificare ulteriormente.

La prima linea della $\displaystyle { \times }$ è quella che va dal $\displaystyle { 3 }$ in basso a sinistra al $\displaystyle { 9 }$ in alto a destra:

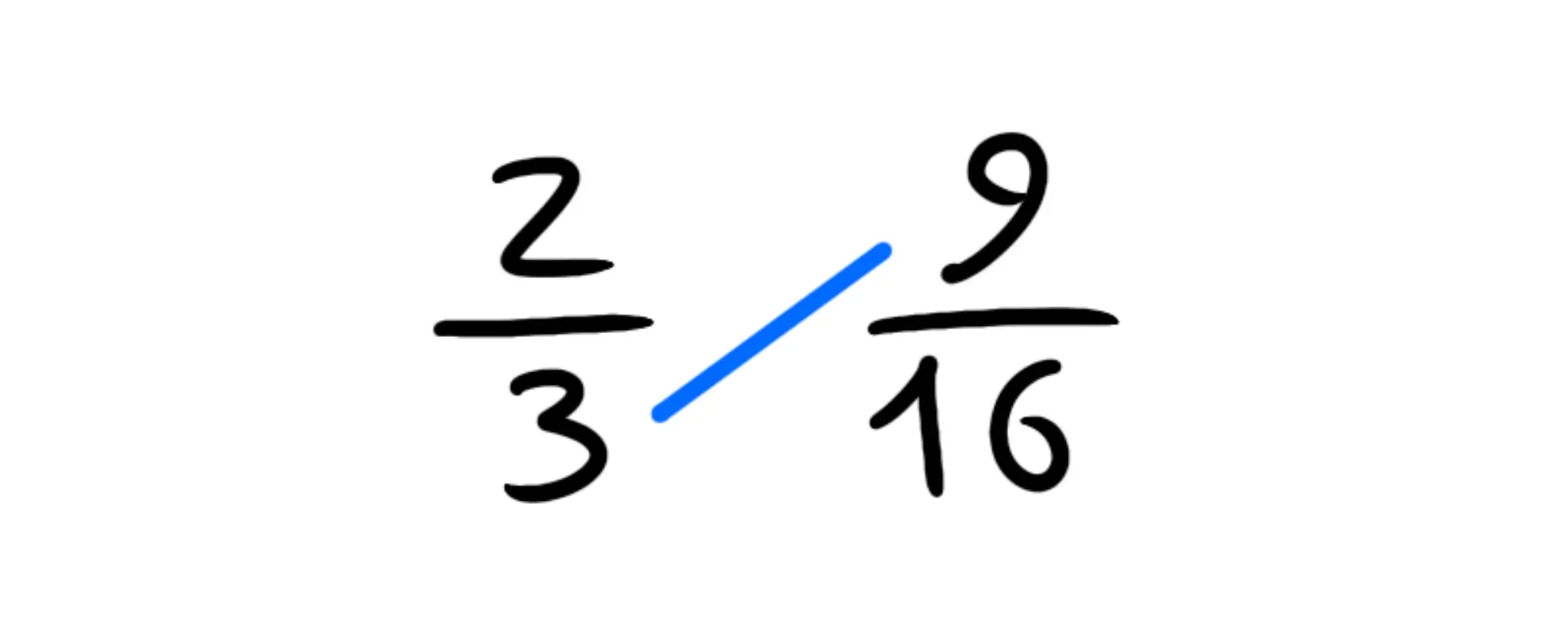
Quindi possiamo semplificare il $\displaystyle { 3 }$ e il $\displaystyle { 9. }$ Entrambi sono divisibili per $\displaystyle { 3, }$ quindi dividiamoli per esso. Quando lo facciamo, tracciamo una sbarra obliqua sul vecchio numero e scriviamo accanto in piccolo il risultato della divisione:

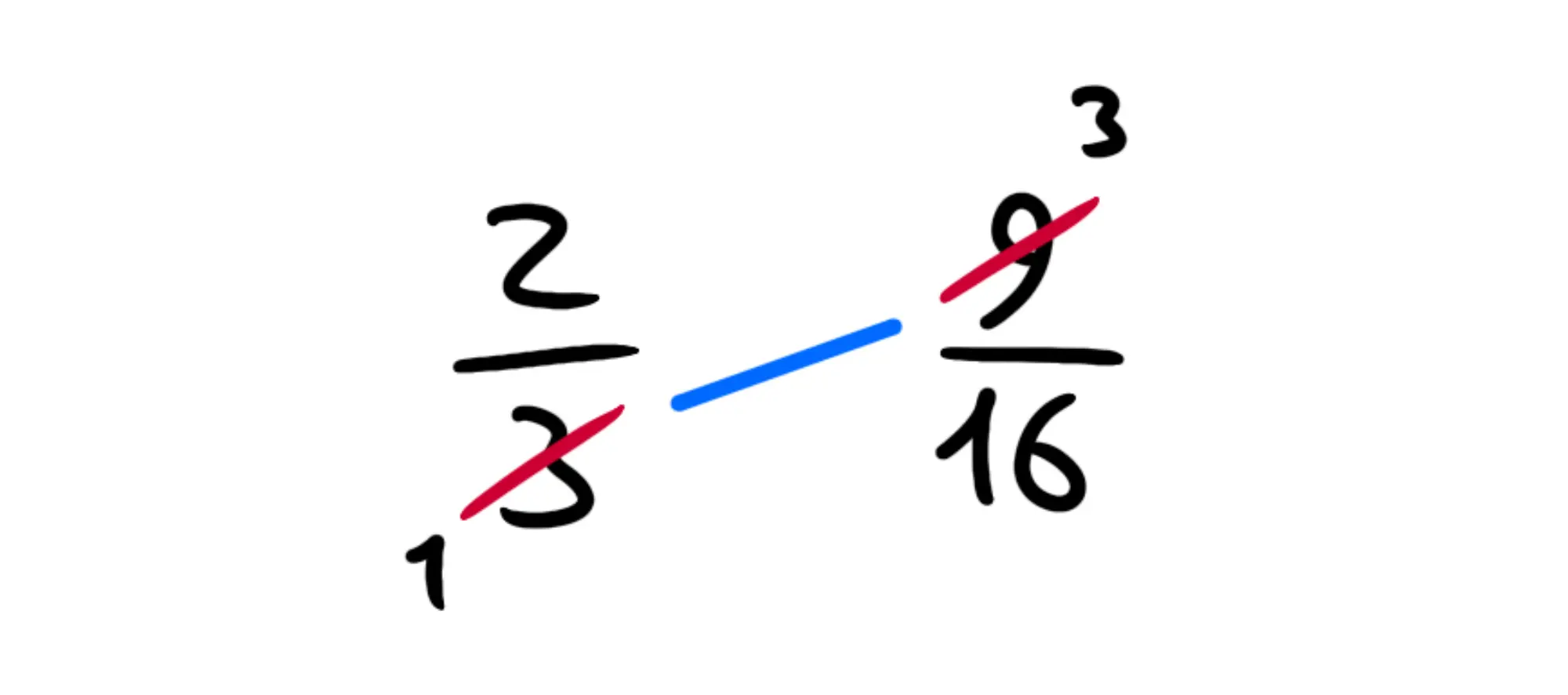
E adesso guardiamo all'altra linea della $\displaystyle { \times : }$

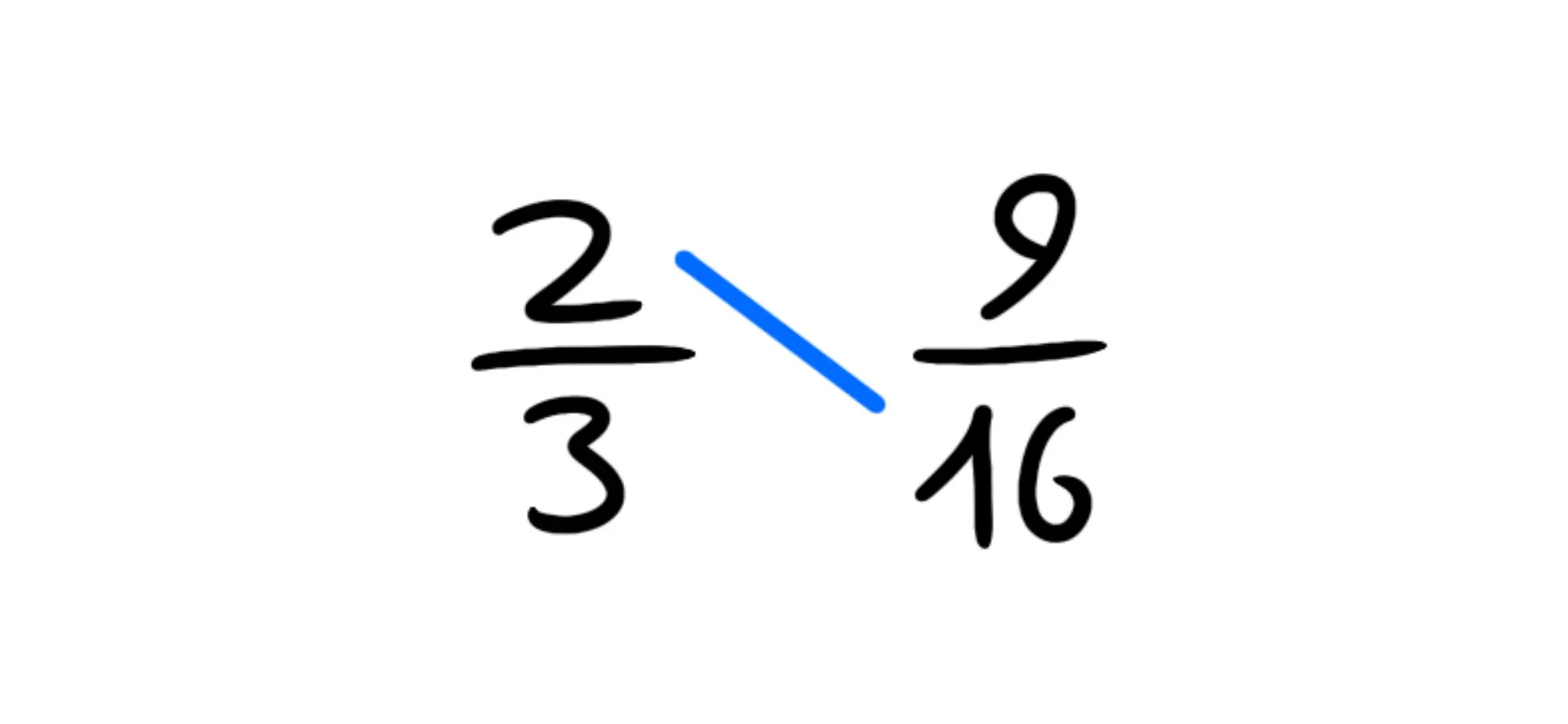
Anche qui, possiamo dividere entrambi i numeri per $\displaystyle { 2, }$ ottenendo:

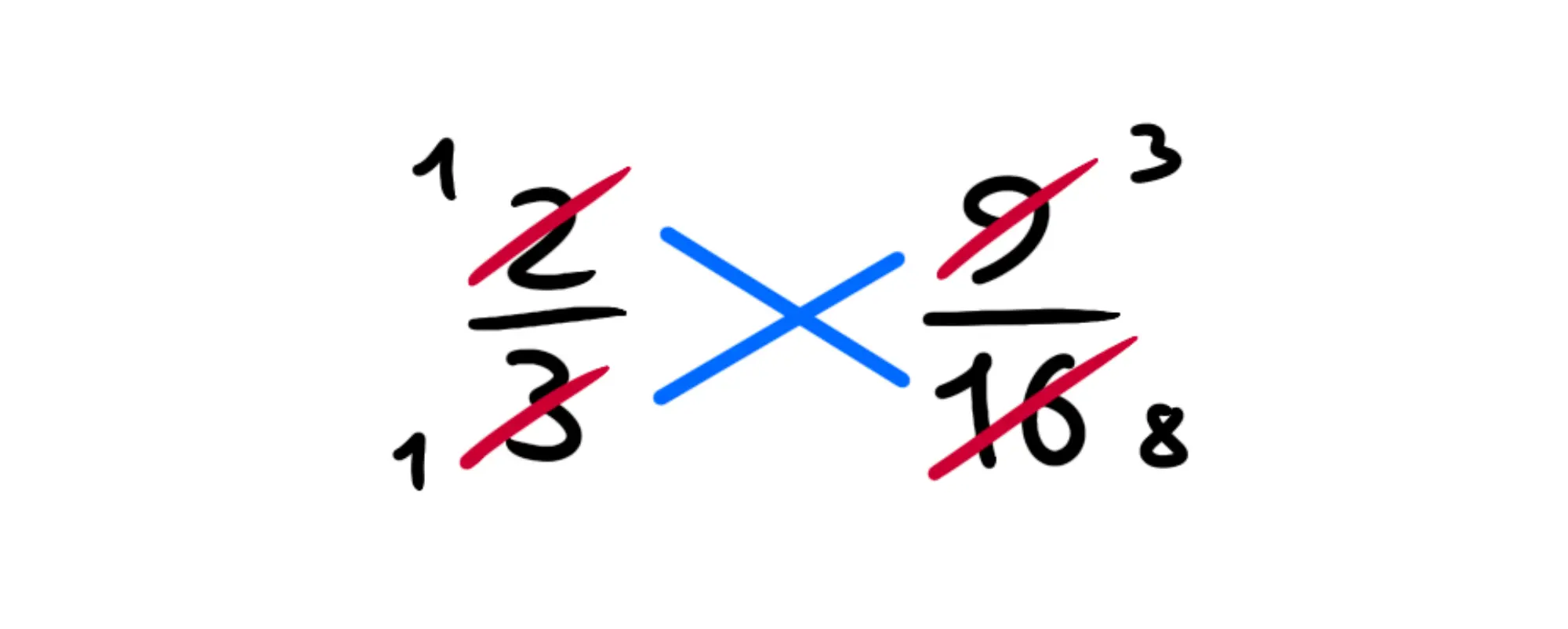
Adesso riscriviamo i nuovi numeri che abbiamo ottenuto al posto di quelli vecchi:

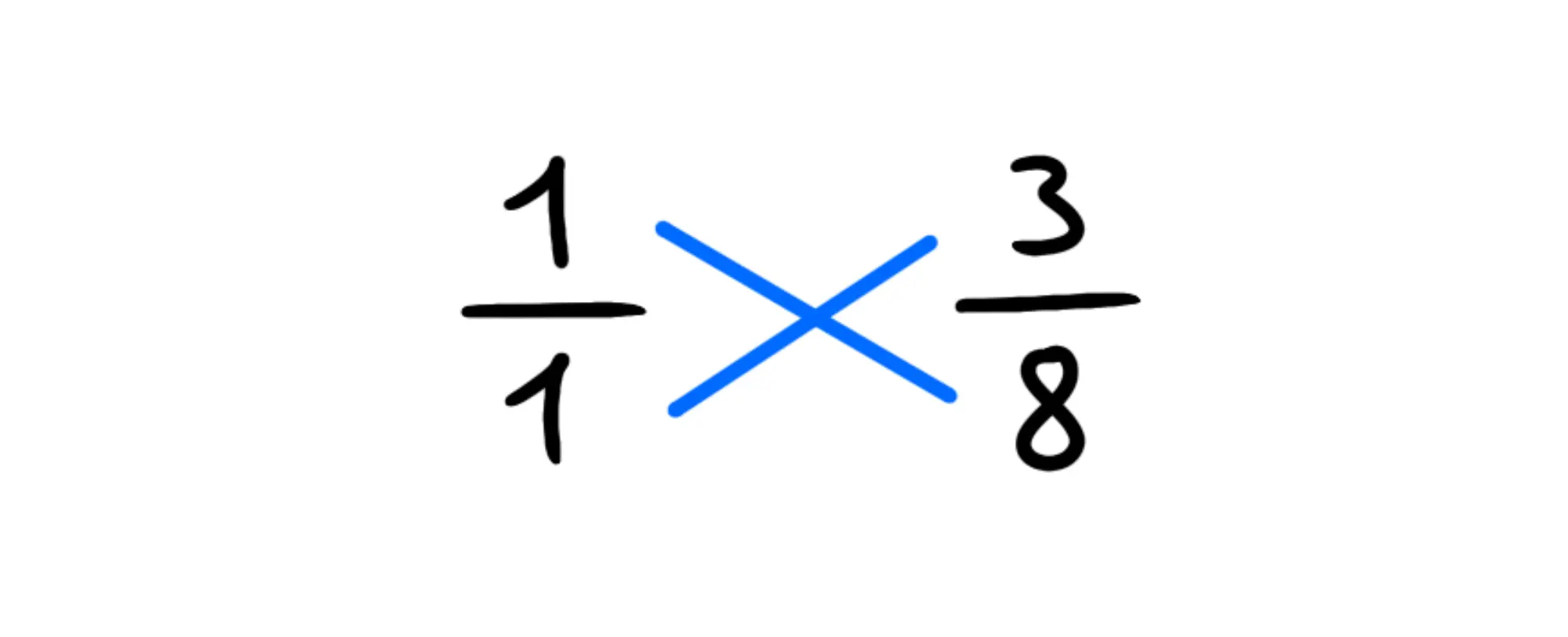
E adesso moltiplichiamo, ottenendo $\displaystyle { {3\over 8}. }$ Visto come i numeri sono usciti molto più piccoli? Altrimenti avreste dovuto fare $\displaystyle { 2\times 9 }$ e $\displaystyle { 3\times 16. }$

Quindi possiamo semplificare in verticale le singole frazioni e poi in obliquo lungo le linee della $\displaystyle { \times , }$ ma mi raccomando, non si può semplificare in orizzontale! In orizzontale si moltiplica soltanto.

Ricordate: verticale e obliquo divido, orizzontale moltiplico.

Vediamo quindi la divisione tra frazioni.

In realtà è piuttosto semplice, infatti basta moltiplicare per il reciproco.

Quindi, se devo fare $\displaystyle { {6\over 5} : {7\over 5}, }$ è uguale a fare $\displaystyle { {6\over 5} \times {5\over 7}, }$ che, semplificando, fa $\displaystyle { {6\over 7}. }$

Infine, vediamo la potenza di una frazione.

Anche questa è abbastanza facile, infatti basta fare la potenza del numeratore e del denominatore. Quindi, per esempio :

$\displaystyle { \left({2\over 3}\right)^2 = {2^2 \over 3^2} = {4\over 9} }$

E anche:

$\displaystyle { \left({3\over 5}\right)^3 = {3^3 \over 5^3} = {27\over 125} }$

Quindi per questa lezione è tutto, se avete letto tutto quanto ed ora siete arrivati fino a qua, siete dei campioni e riuscirete a risolvere qualsiasi problema con le frazioni. Se volete studiare le espressioni con le frazioni, (cliccate qui 👈).