La divisione tra polinomi è utile in molte situazioni e spesso ci aiuta a semplificare i calcoli, tenerla a mente è importante anche perché si tratta di un’operazione di base e potrebbe capitare in alcuni esercizi.
Un teorema dell’algebra afferma che è sempre possibile dividere un polinomio per qualsiasi altro polinomio e avere come risultato due nuovi polinomi, il polinomio quoziente e il polinomio resto.
Cioè possiamo sempre riscrivere nella seguente forma:
Per svolgere la divisione basta seguire pochi semplici passaggi e ripeterli. Bisogna prima ricordare che se dividiamo un polinomio per un polinomio di grado superiore il quoziente sarà il polinomio nullo e il resto sarà il polinomio di partenza:
Esempio:
Chiarito questo, passiamo all’algoritmo di svolgimento della divisione.
Per prima cosa scriviamo all'interno di una tabella di questo tipo il polinomio di partenza e poi il divisore, ordinando i termini in modo decrescente secondo il grado (se il polinomio non è completo si scrive uno 0 al posto dei termini mancanti):
Esempio:
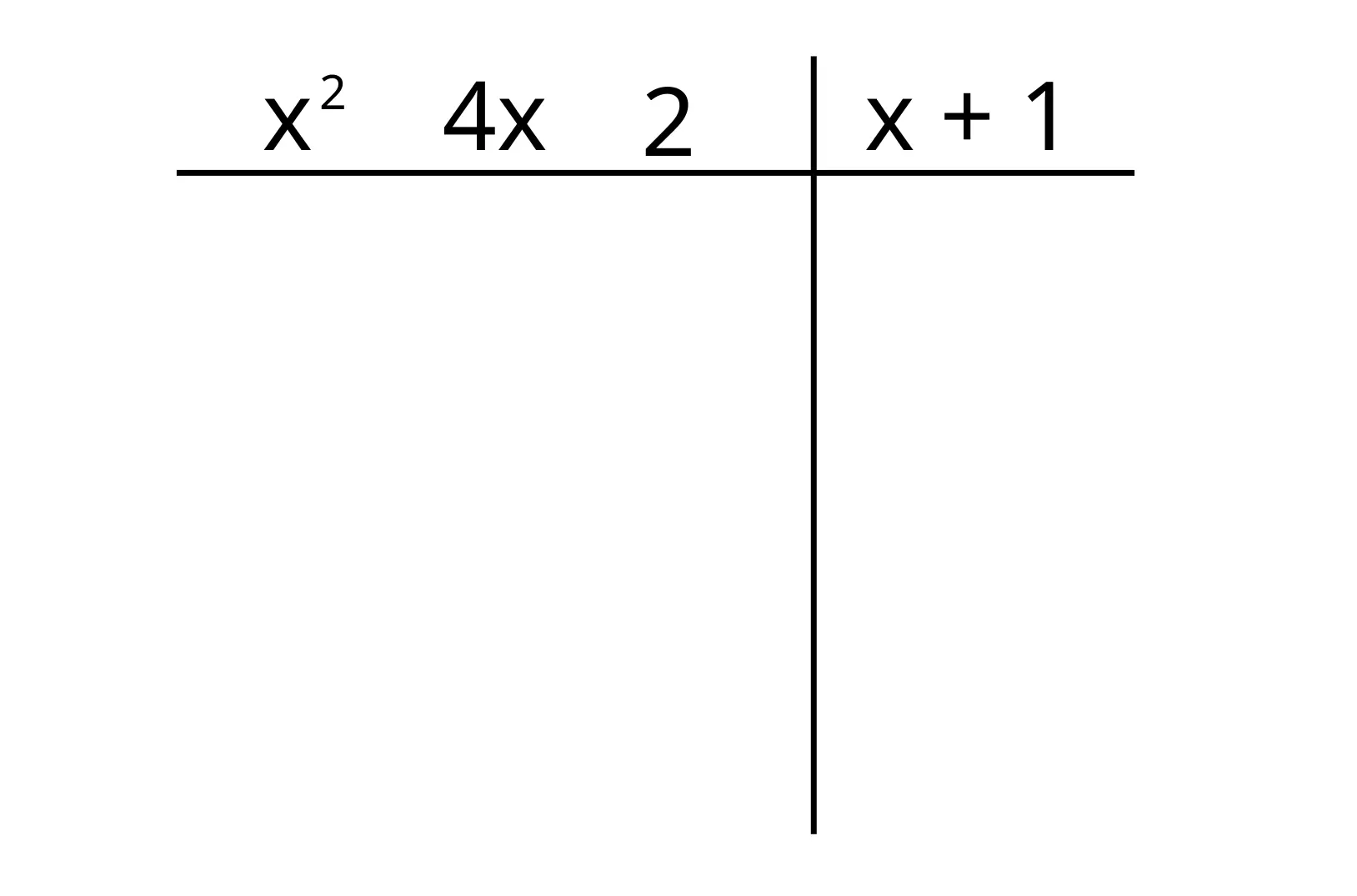
Fatto questo, dividiamo il primo termine del polinomio di partenza con il primo termine del divisore e scriviamo il risultato sotto al divisore (semplice divisione tra monomi trattata nella lezione sui monomi, clicca qui 👈):
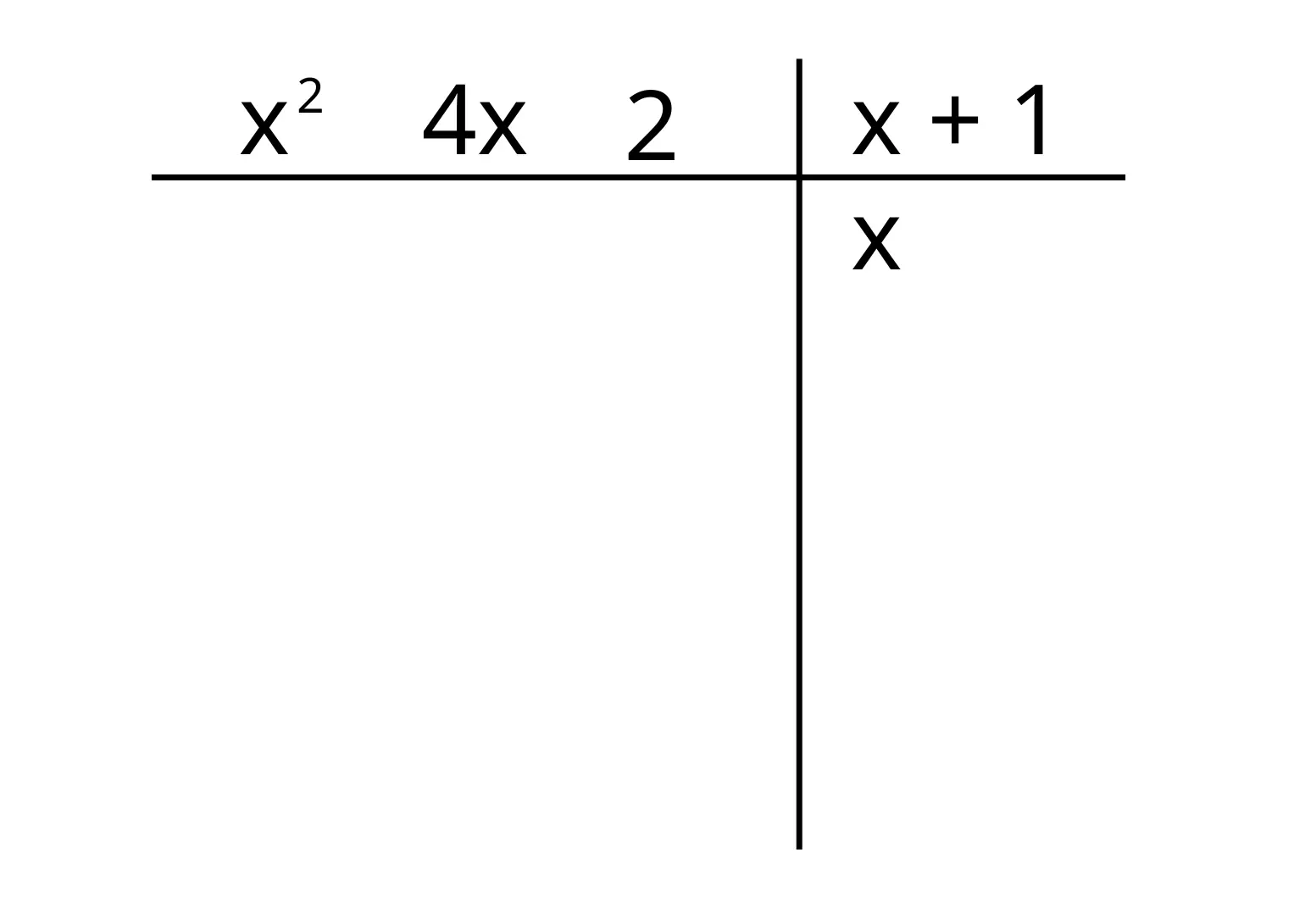
Poi moltiplichiamo quest’ultimo per ogni termine del divisore e scriviamo i risultati cambiati di segno sotto i termini di grado corrispondente del polinomio di partenza:
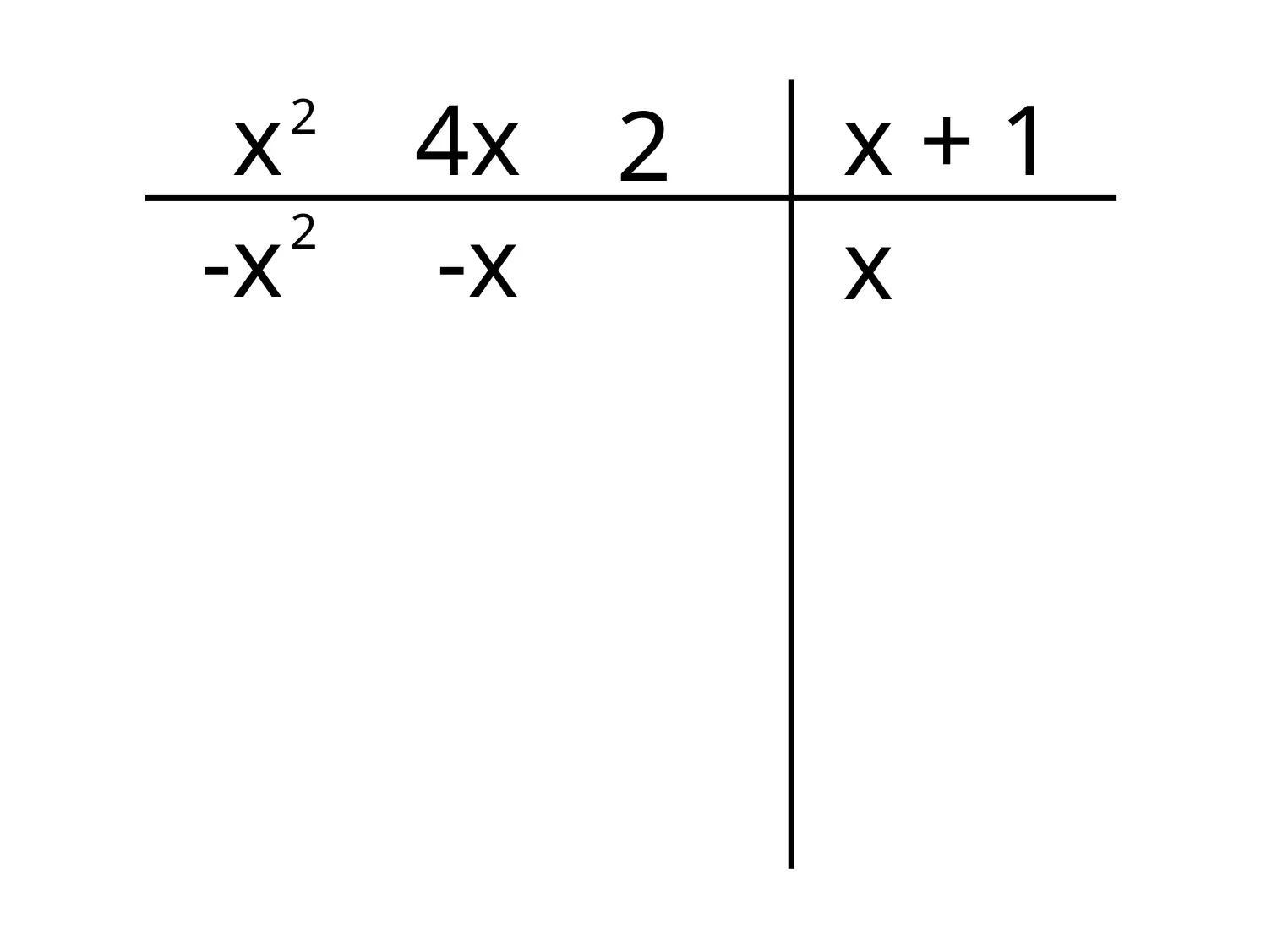
Ora facciamo la somma tra i termini del polinomio e i termini appena scritti al disotto di essi e scriviamo sotto il risultato (separato da una linea orizzontale):
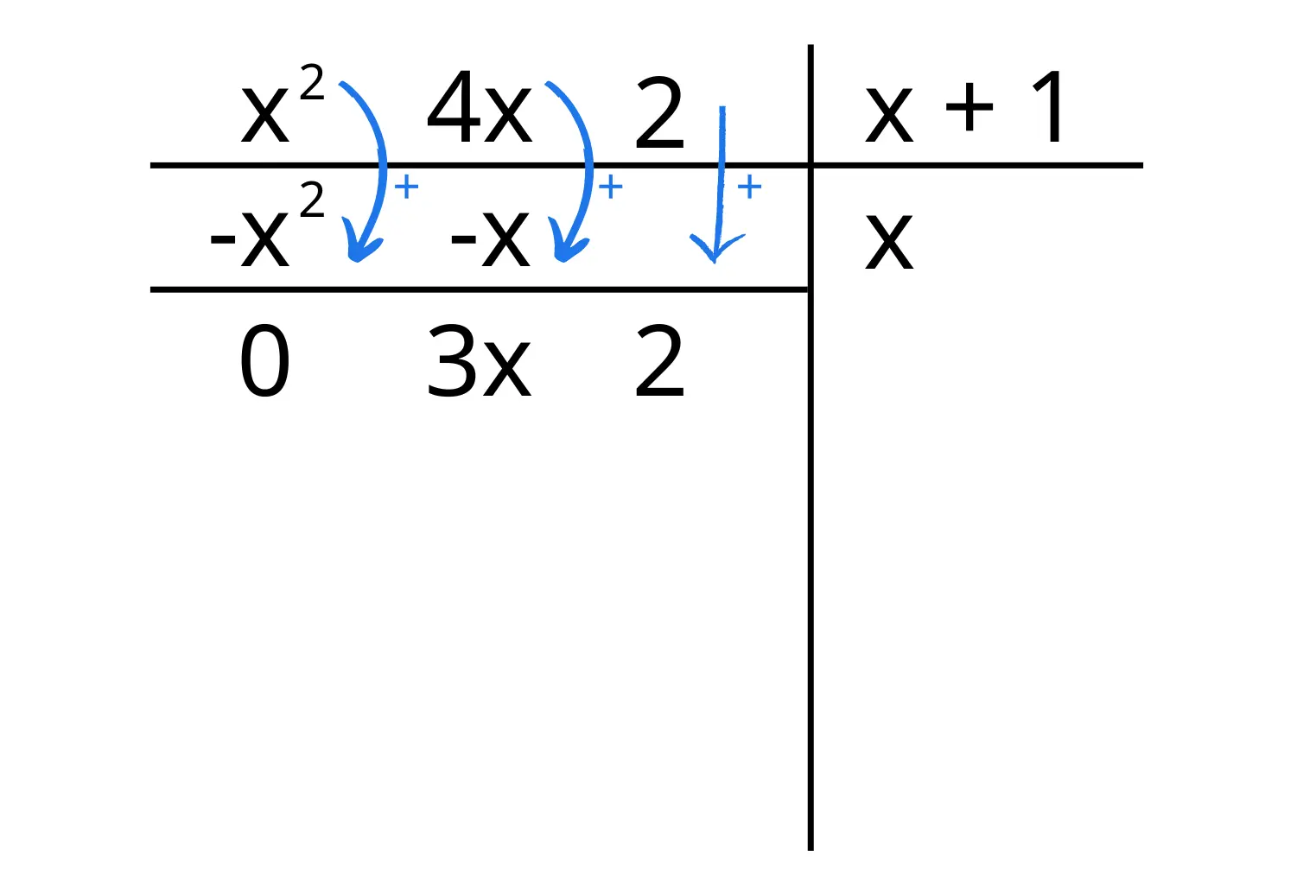
Ripetiamo il processo finché il polinomio a sinistra è di grado inferiore al divisore, quando è di grado superiore ci fermiamo. Il polinomio a sinistra sarà il nostro resto, mentre quello a destra il quoziente.
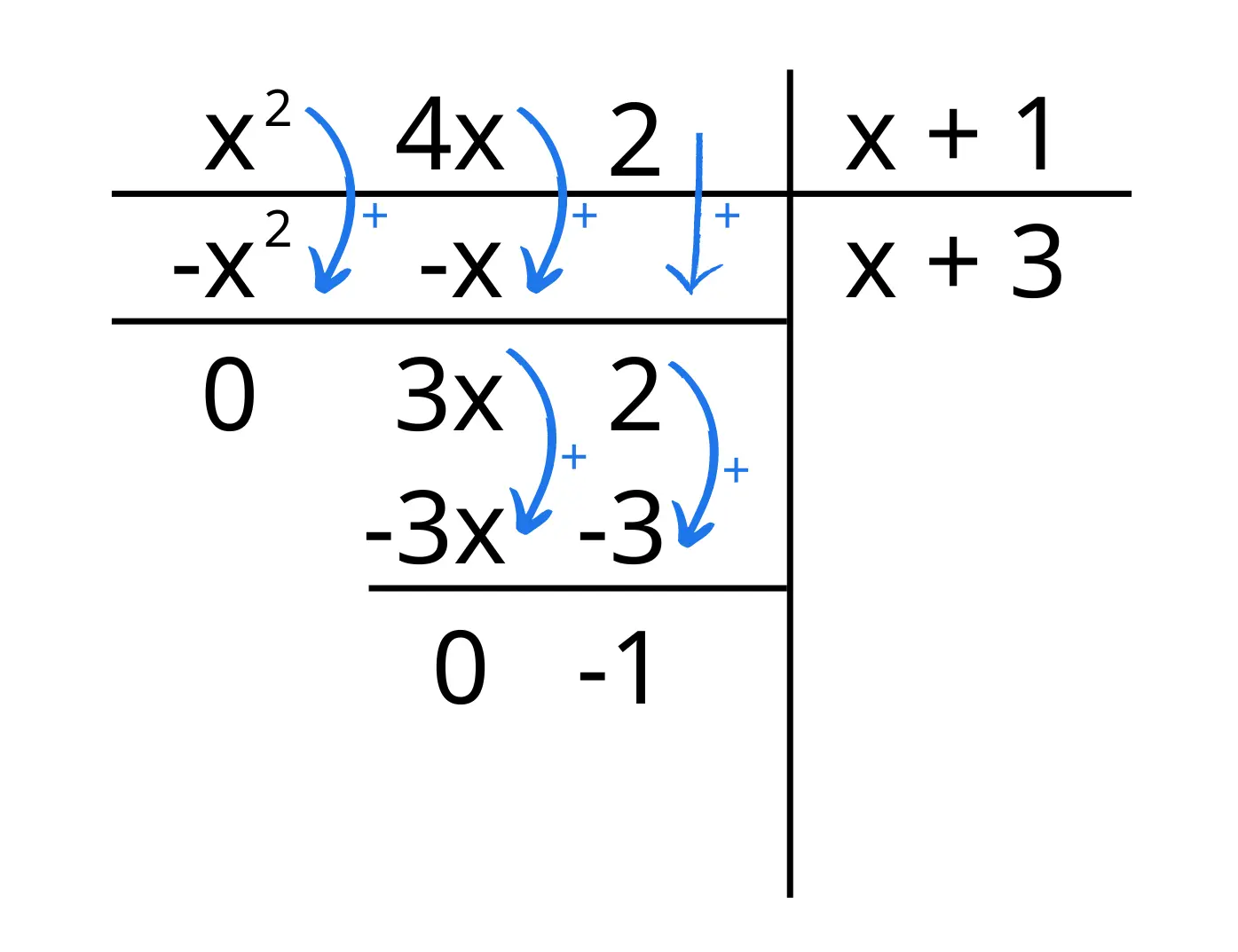
Quindi avremo
Speriamo di avervi reso chiaro il concetto, ricordate che se il divisore è di primo grado potete anche usare la regola di Ruffini per la divisione.