Grafico delle funzioni goniometriche

Seno e coseno

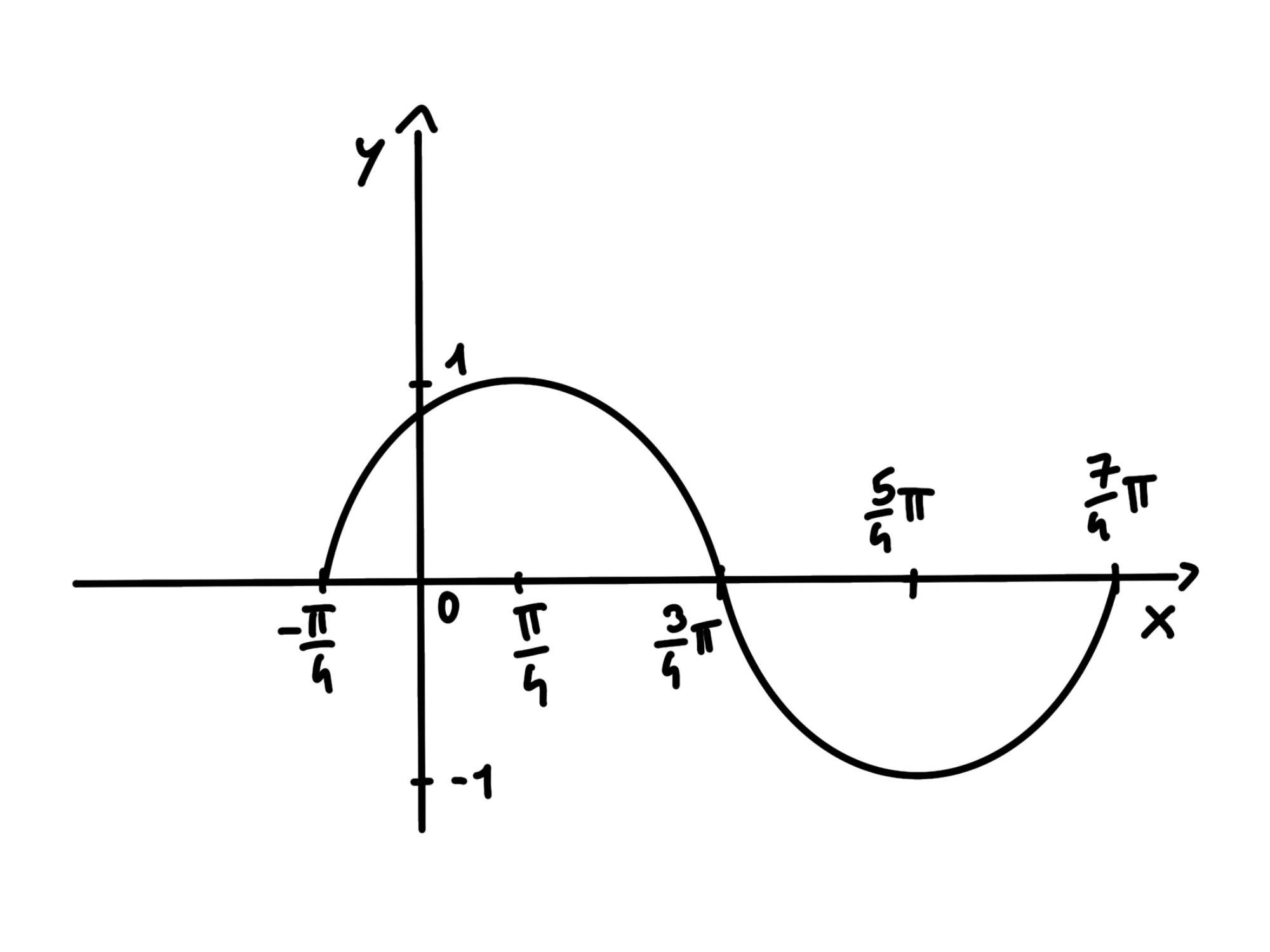
Le funzioni seno e coseno hanno entrambe periodo $\displaystyle { 2\pi, }$ dunque ci basterà trovare il grafico tra $\displaystyle { 0 }$ e $\displaystyle { 2\pi }$ e poi ripeterlo.

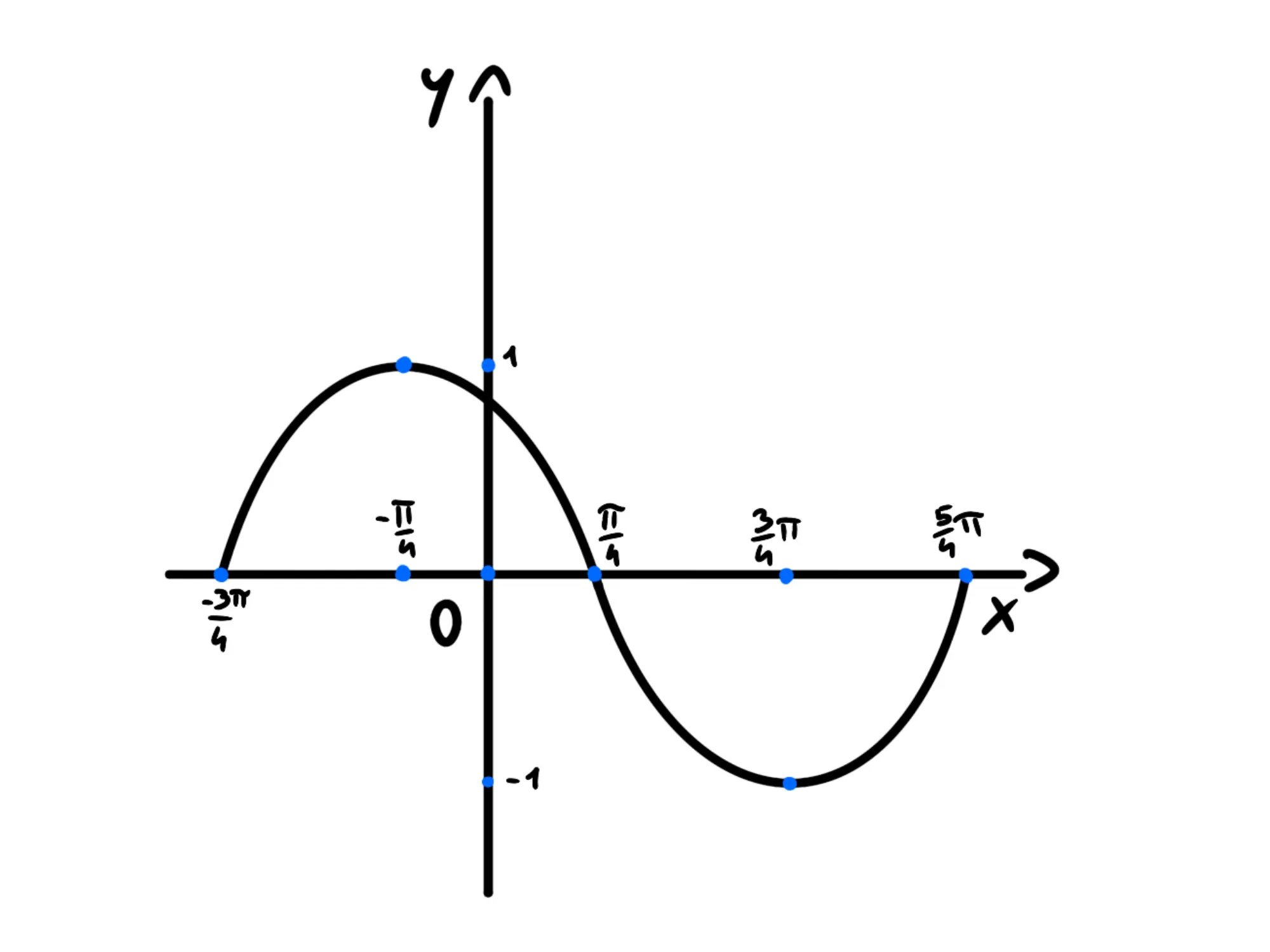
Il seno di $\displaystyle { 0 }$ è uguale a $\displaystyle { 0, }$ quindi il suo grafico passa per l'origine. Raggiunge il suo massimo a $\displaystyle { \pi\over 2 }$ quando è uguale ad $\displaystyle { 1, }$ torna ad essere $\displaystyle { 0 }$ quando arriviamo a $\displaystyle { \pi, }$ raggiunge il suo minimo a $\displaystyle { {3\pi\over 2} }$ quando vale $\displaystyle { -1 }$ e a $\displaystyle { 2\pi }$ completa il periodo tornando a $\displaystyle { 0: }$

Inserendo altri punti notiamo che si muove come un onda:

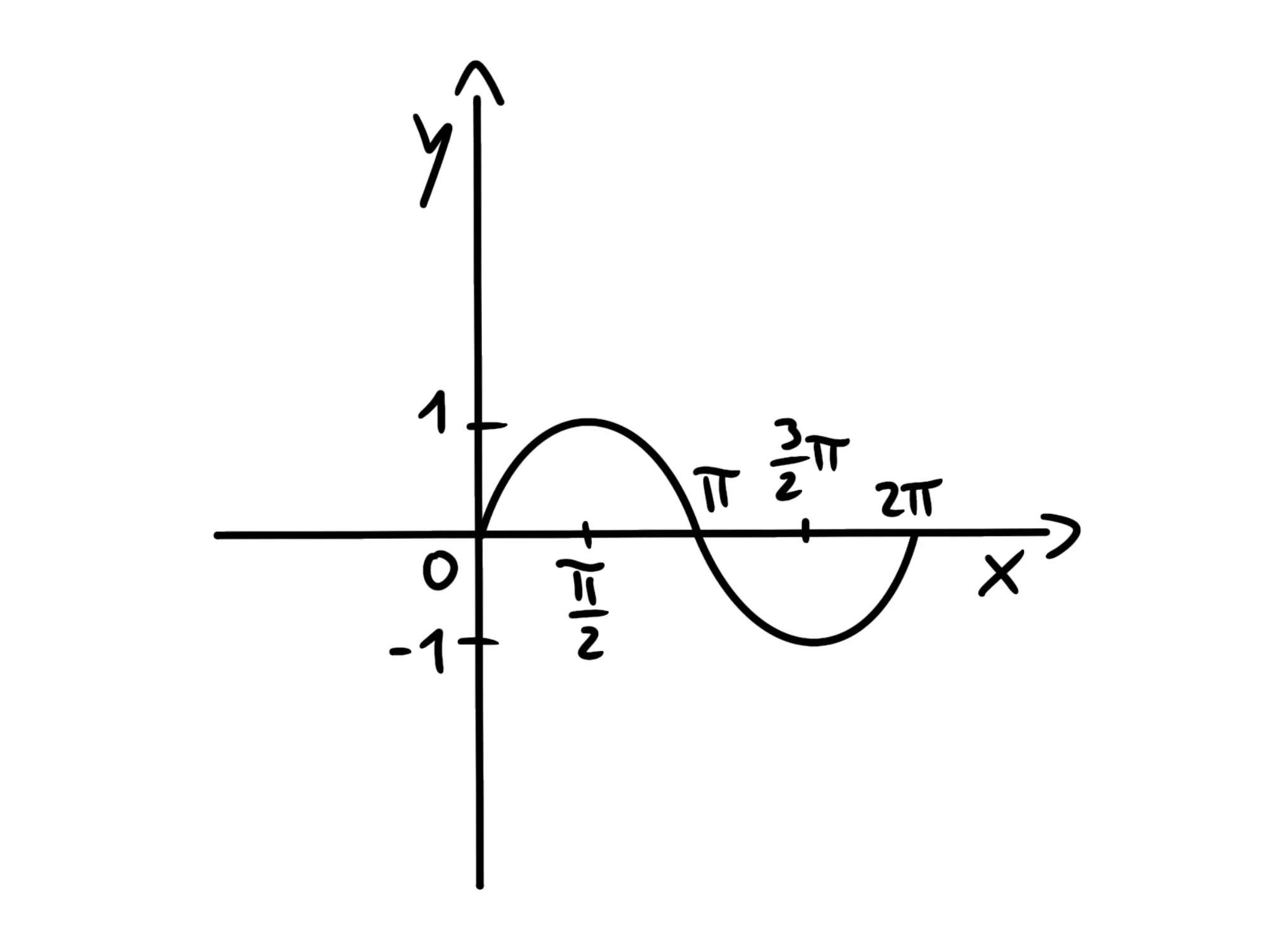
Adesso che abbiamo trovato un periodo del grafico, ci basta ripeterlo per ottenere le altre parti:

Siccome $\displaystyle { \cos(x) = \sin({\pi\over 2} -x), }$ il grafico del coseno sarà uguale a quello seno ma traslato.

Il coseno, infatti, invece che partire da $\displaystyle { 0 }$ parte da $\displaystyle { 1: }$

Inserendo altri punti otteniamo infatti:

Avendo completato il periodo, possiamo ripeterlo e disegnare le altre parti del grafico:

Notiamo che infatti, come abbiamo detto prima, si tratta del grafico di $\displaystyle { \sin(x) }$ traslato di $\displaystyle { {\pi\over 2} }$ a sinistra.

Tangente e cotangente

La tangente e la cotangente hanno invece come periodo $\displaystyle { \pi. }$ Quindi ci basterà fermarci a $\displaystyle { \pi }$ e ripetere quello che abbiamo trovato.

La tangente di $\displaystyle { 0 }$ è uguale a $\displaystyle { 0, }$ dunque il suo grafico passa per l'origine.

Tende a $\displaystyle { +\infty }$ quando la $\displaystyle { x }$ tende a $\displaystyle { \pi\over 2 }$ e poi salta a $\displaystyle { -\infty }$ per poi tornare a $\displaystyle { 0 }$ quando la $\displaystyle { x }$ vale $\displaystyle { \pi, }$ completando così il periodo:

Possiamo trovare le altre parti del grafico ripetendo il periodo:

Notiamo che quindi presenterà asintoti verticali a $\displaystyle { {\pi\over 2} + 2k\pi }$ dove $\displaystyle { k }$ è un qualsiasi numero intero.

La cotangente, invece, parte a $\displaystyle { +\infty, }$ arriva a $\displaystyle { 0 }$ quando la $\displaystyle { x }$ vale $\displaystyle { {\pi\over 2} }$ e tende a $\displaystyle { -\infty }$ quando la $\displaystyle { x }$ tende a $\displaystyle { \pi: }$

Ripetendo il periodo otteniamo:

Quindi la cotangente avrà asintoti verticali $\displaystyle { x= \pi + 2k\pi }$ dove $\displaystyle { k }$ è un qualsiasi numero intero.

Ampiezza, periodo e fase

Abbiamo visto che il seno e il coseno sono sempre compresi tra $\displaystyle { 1 }$ e $\displaystyle { -1. }$ Se però moltiplichiamo il tutto per $\displaystyle { 2, }$ allora sarà compreso tra $\displaystyle { 2 }$ e $\displaystyle { -2: }$

Il coefficiente davanti al seno o al coseno ci dice quindi il massimo e il minimo della funzione e viene chiamato ampiezza .

Se quindi prendiamo la funzione $\displaystyle { f(x)=5\sin(x), }$ la sua ampiezza sarà $\displaystyle { 5 }$ e il suo grafico sarà:

Oltre a mettere un coefficiente davanti alla funzione, possiamo mettere pure un coefficiente davanti alla $\displaystyle { x }$ che sta nell'argomento.

Com'è il grafico, per esempio, di $\displaystyle { \cos(2x)? }$

L'argomento, essendo il doppio di $\displaystyle { x, }$ aumenterà il due volte più velocemente di $\displaystyle { x, }$ quindi ci metterà metà spazio per completare un periodo:

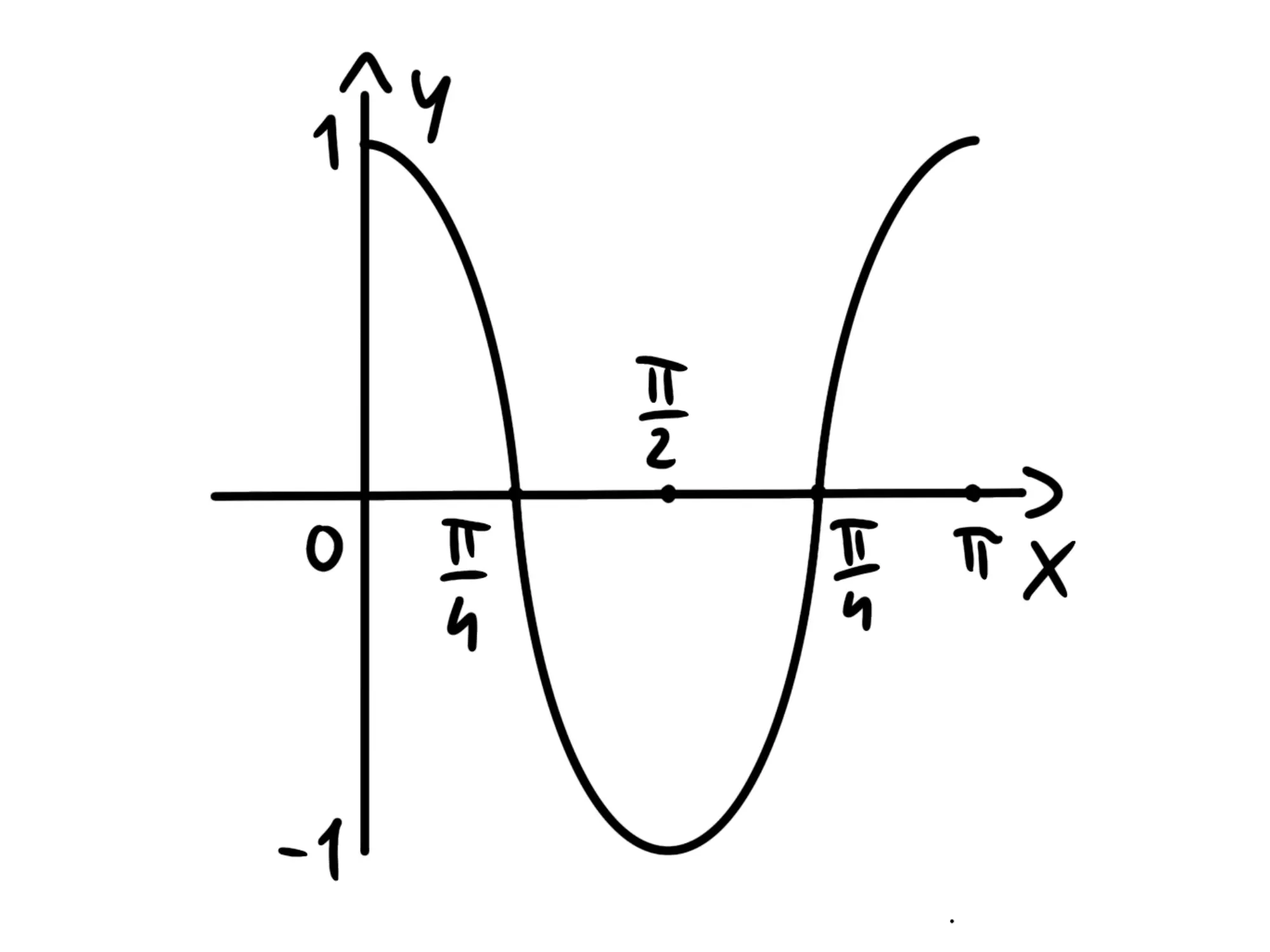
Se il coseno aveva come periodo $\displaystyle { 2\pi, }$ il coseno di $\displaystyle { 2x }$ avrà infatti periodo di $\displaystyle { \pi. }$

In generale, se abbiamo una funzione $\displaystyle { y=\cos(wx), }$ il suo periodo $\displaystyle { T }$ varrà $\displaystyle { {2\pi\over w}: }$

$\displaystyle { T={2\pi\over w} }$

Possiamo poi aggiungere una costante. Per esempio potremmo avere $\displaystyle { y=\cos(x) + 1. }$ Per rappresentarla, ci basta alzare di $\displaystyle { 1 }$ tutto il grafico del coseno.

Infatti, l'equazione della funzione ci dice che per ogni $\displaystyle { x }$ calcoliamo il suo coseno e poi lo alziamo di $\displaystyle { 1. }$

Il grafico di $\displaystyle { \cos(x) + 1 }$ sarà quindi:

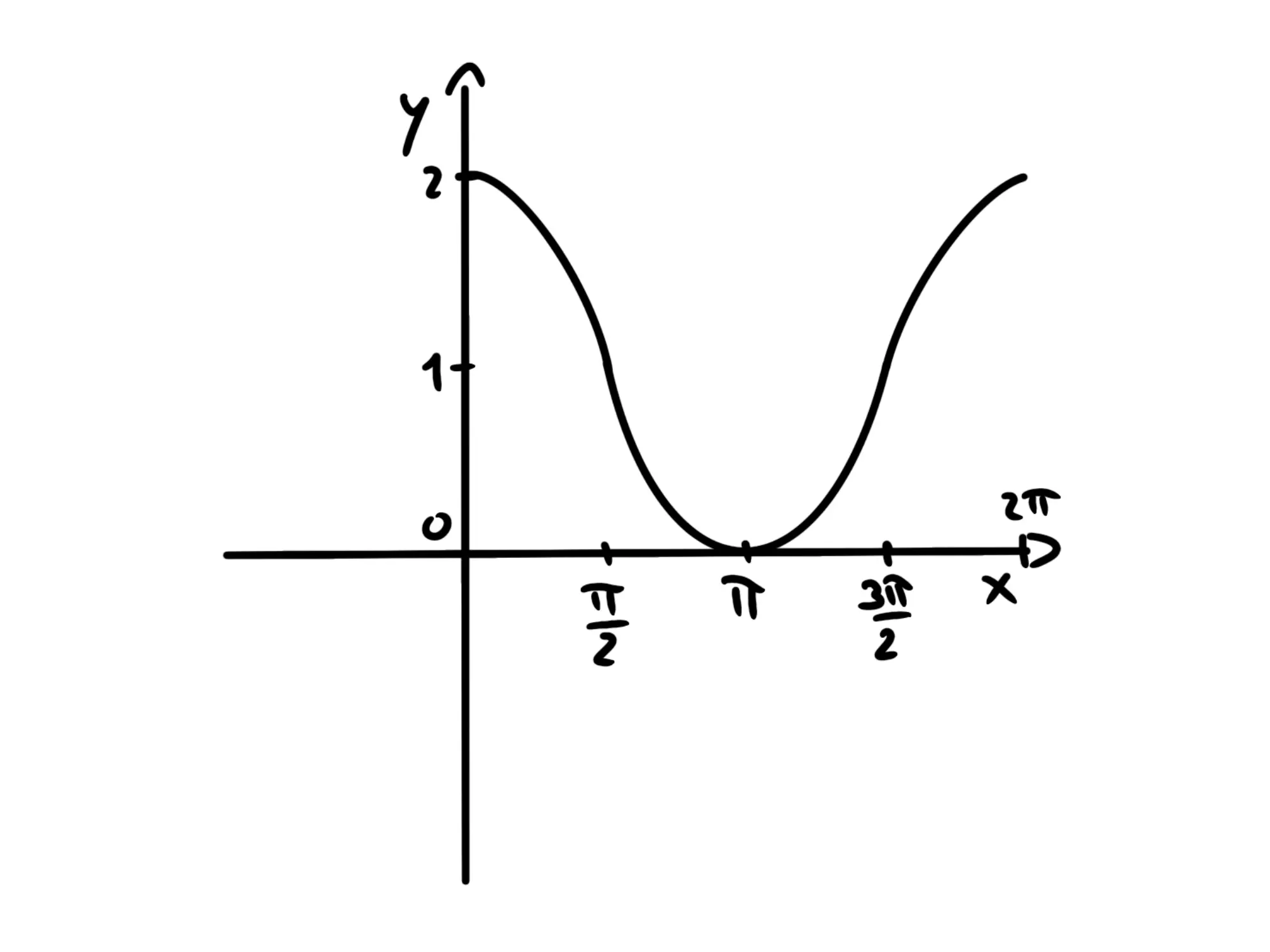
Infine, possiamo aggiungere una costante dentro l'argomento. Per esempio potremmo avere $\displaystyle { \cos(x + {\pi\over 4}). }$ In alcuni casi possiamo usare gli archi associati per ricondurlo ad una funzione più semplice, ma non sempre è possibile e spesso dobbiamo lasciare quella costante lì dentro, chiamata fase .

Cosa fa la fase al nostro grafico? Se chiamiamo la nostra fase $\displaystyle { \phi }$ (lettera greca che si leggere "phi" ("fi") che viene solitamente usata per indicare la fase), quello che noi stiamo facendo è mettere $\displaystyle { x+\phi }$ al posto della $\displaystyle { x. }$ Se vi ricordate, questo significa traslare a sinistra il grafico di $\displaystyle { \phi }$ unità.

Nel nostro caso, quindi, se il grafico di $\displaystyle { \cos(x) }$ era:

il grafico di $\displaystyle { \cos(x + {\pi\over 4}) }$ sarà:

Se la costante che sommiamo è negativa, dovremo spostare il grafico verso destra. Quindi il grafico di $\displaystyle { \cos(x-{\pi\over 4}) }$ sarà: