Funzioni trigonometriche

Cosa devo già sapere?

Da sapere:

Teorema di Pitagora

Quali sono le funzioni trigonometriche?

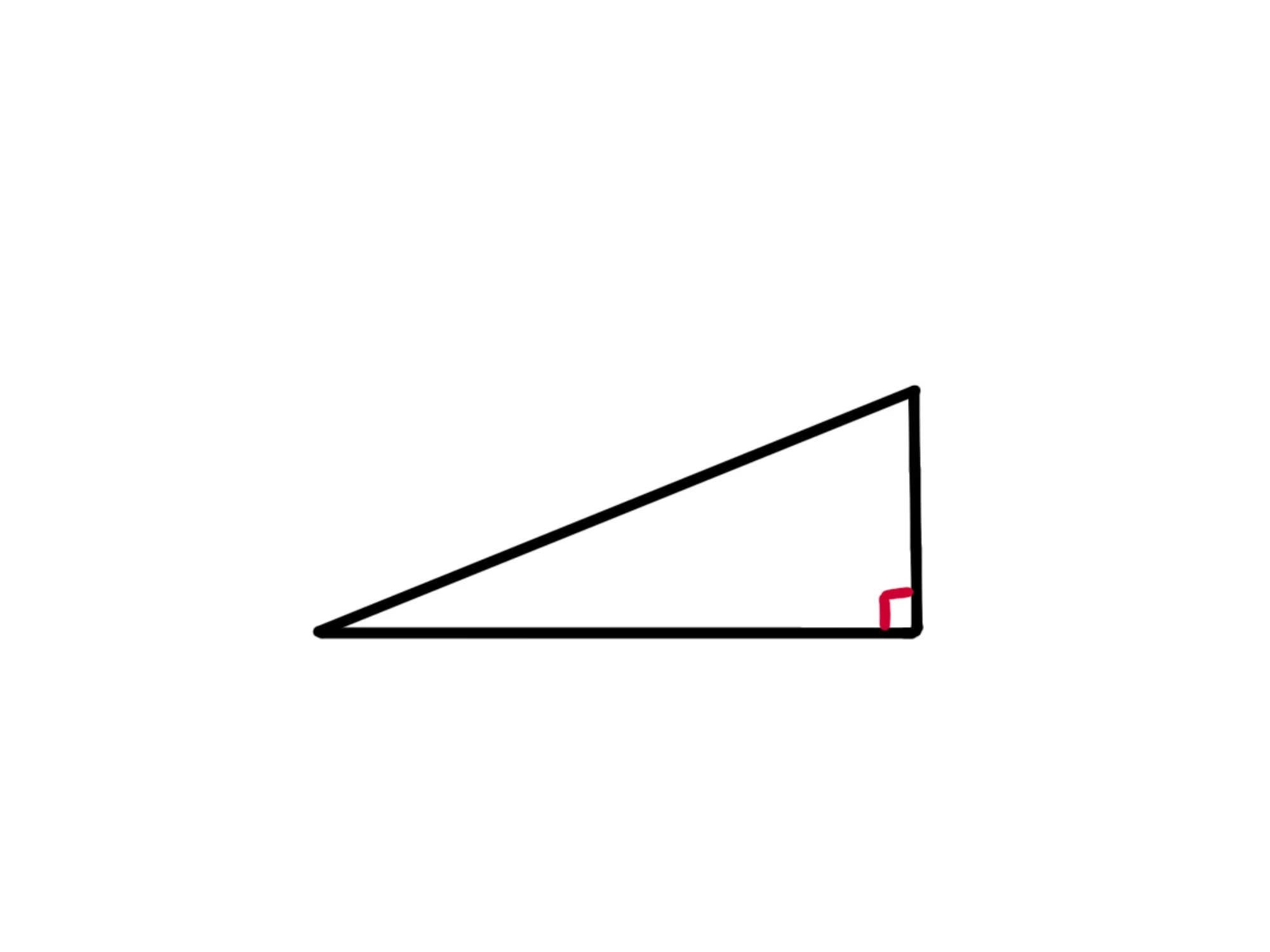
Prendiamo un triangolo rettangolo:

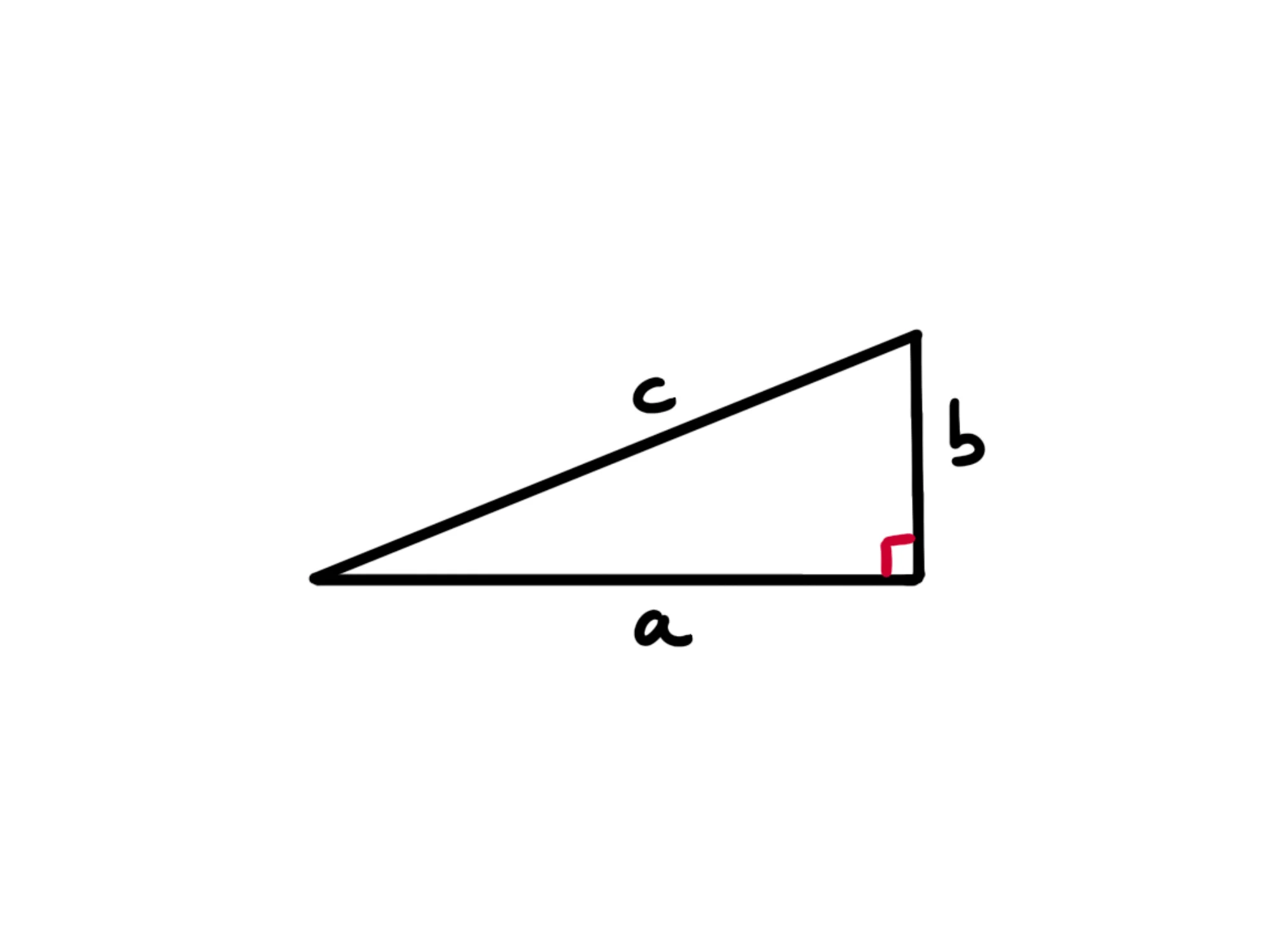
Chiamiamo la sua ipotenusa c e i suoi cateti a e b:

Chiamiamo i due angoli acuti \alpha e \beta :

Questo grafico ci permetterà di definire le principali funzioni trigonometriche. Partiamo dal seno:

Il seno di un angolo equivale al rapporto tra il cateto opposto e l'ipotenusa.

Quindi nel nostro grafico abbiamo:

\sin(\alpha) = {b\over c}

\sin(\beta) = {a\over c}

La funzione seno, spesso abbreviata con seno, di un angolo \theta (theta) si scrive in italiano \textrm{sen} \, \theta , ma qui su Theroemz solitamente usiamo la notazione inglese, quella che compare su quasi tutte le calcolatrici, che è \sin\theta . Non confondetevi, sono la stessa cosa. Anche se vanno bene entrambe le notazioni, il vostro prof potrebbe chiedervi di usare solo la notazione italiana.

L'importante, però, è aver capito come si definisce la funzione seno.

Possiamo quindi passare alla funzione coseno:

Il coseno di un angolo è il rapporto tra il cateto adiacente e l'ipotenusa.

Quindi nel grafico abbiamo:

\cos(\alpha) = {a\over c}

\cos(\beta) = {b\over c}

E' molto simile alla funzione seno, dovete solo prendere il cateto che sta "vicino" all'angolo invece che quello che sta "lontano".

Al contrario del seno, sia in inglese che in italiano il coseno di un angolo \theta si indica come \cos(\theta).

E' importante saper usare le formule che derivano dalla definizione di queste due funzioni. Per esempio, siccome:

\cos(\beta) = {b\over c}

Dobbiamo avere:

b = c \cdot \cos(\beta)

Cioè, in generale, un cateto è uguale all'ipotenusa per il coseno dell'angolo adiacente.

La cosa importante da comprendere è proprio questo concetto di angolo opposto e angolo adiacente e ricordarsi "seno-opposto" e "coseno-adiacente" perché la maggior parte degli errori è causata dalla confusione tra le due funzioni.

Siccome il cateto è sempre minore dell'ipotenusa (o uguale nel caso di un triangolo degenere), sia il seno che il coseno dovranno essere sempre minori o uguali ad 1.

Definiamo poi la funzione tangente come il rapporto tra il seno e il coseno:

\tan(\alpha) = {\sin(\alpha)\over \cos(\alpha)}

Effettivamente cosa rappresenta? Possiamo riscriverla come:

\tan(\alpha) = {\sin(\alpha) \over \cos(\alpha)}= {{b\over c} \over {a\over c}} = {b\over c} \cdot {c\over a}={b\over a}

Quindi è uguale al rapporto tra il cateto opposto e quello adiacente.

Ora che le abbiamo definite, vediamo qualche proprietà delle funzioni trigonometriche:

Proprietà

Siccome, nel grafico di prima, abbiamo \cos(\beta) = {b\over c} e anche \sin(\alpha) = {b\over c}, dobbiamo avere \cos(\beta) = \sin(\alpha).

Siccome la somma degli angoli interni di un triangolo è sempre 180° e in un triangolo rettangolo un angolo è uguale a 90°, la somma degli altri due deve essere 90° perché così otteniamo in totale 180°. Quindi avremo:

\alpha + \beta = 90°

\alpha = 90° - \beta

Quindi, sostituendo nella formula di prima, otteniamo:

\cos(\beta) = \sin(\alpha)

\cos(\beta) = \sin(90° - \beta)

Per lo stesso ragionamento abbiamo:

\sin(\beta) = \cos(90°-\beta)

Questo è vero per qualsiasi angolo \beta.

La proprietà che stiamo per analizzare è talmente importante che viene chiamata l'identità fondamentale della trigonometria.

Ricordiamo che:

\cos(\alpha) = {a\over c}

\sin(\alpha)= {b\over c}

E dunque:

[\cos(\alpha)]^2 = {a^2\over c^2}

[\sin(\alpha)]^2 = {b^2 \over c^2}

per semplificare la scrittura, [\cos(\alpha)]^2 e [\sin(\alpha)]^2 vengono solitamente scritti come \cos^2(\alpha) e \sin^2(\alpha).

Quindi avremo:

\cos^2(\alpha) + \sin^2(\alpha) = {a^2 \over c^2} + {b^2 \over c^2}= a^2 + b^2 \over c^2

per il Teorema di Pitagora dobbiamo avere a^2 + b^2 = c^2 e quindi:

\cos^2(\alpha) + \sin^2(\alpha) = {a^2 + b^2 \over c^2} = {c^2 \over c^2}

\cos^2(\alpha) + \sin^2(\alpha) = 1

Cioè il coseno quadro più il seno quadro dello stesso angolo equivale sempre ad 1.