Funzioni goniometriche

Cosa devo già sapere?

Da sapere:

Funzioni trigonometriche

Cosa sono?

Avevamo già incontrato le funzioni trigonometriche definendole usando i triangoli rettangoli. In realta, conviene studiarle utilizzando una circonferenza di raggio 1, con la quale potremo definire pure altre funzioni goniometriche.

Prendiamo quindi questa circonferenza incentrata nell'origine e con raggio 1, che chiameremo circonferenza goniometrica:

Prendiamo ora un punto su questa circonferenza:

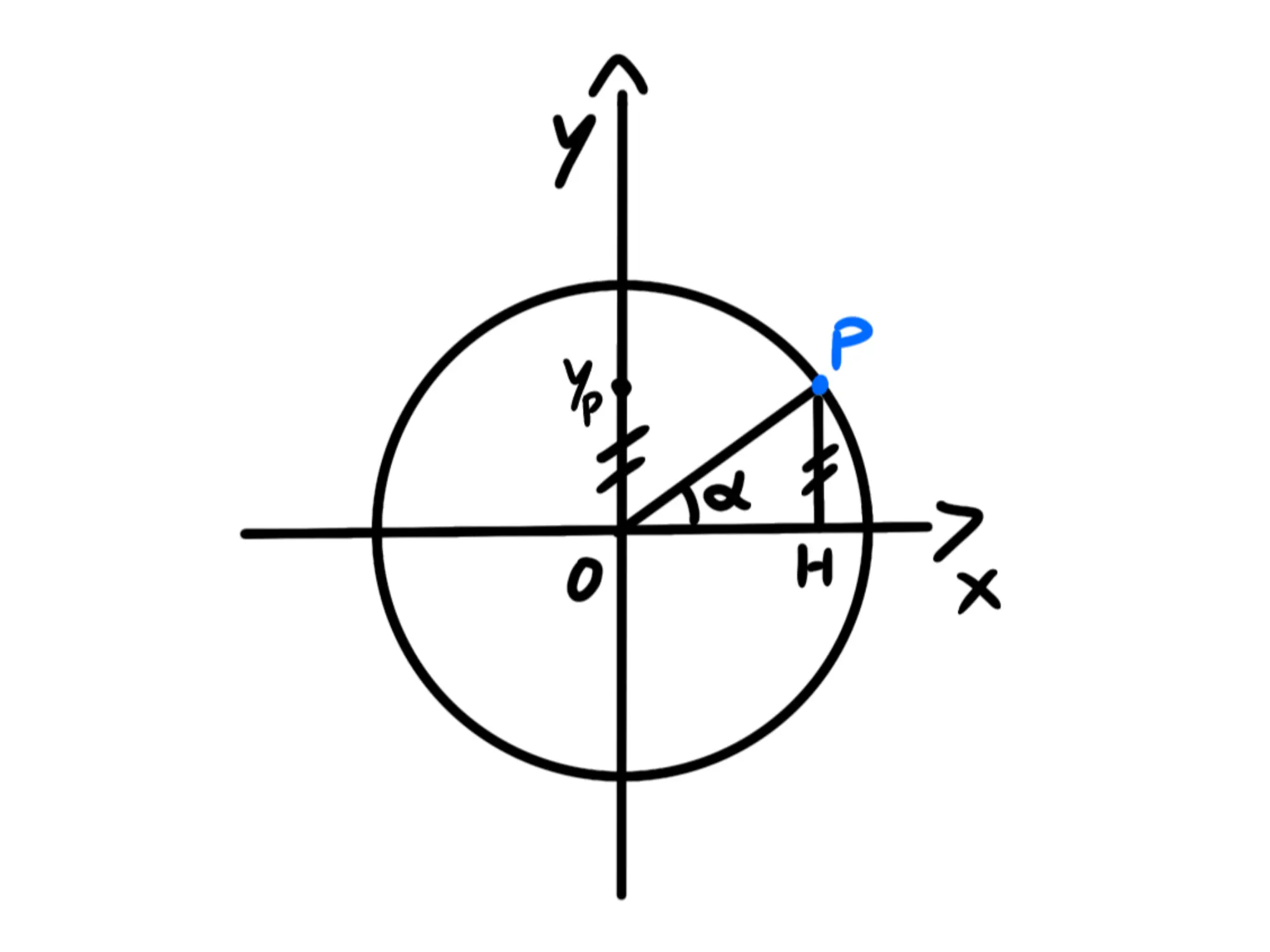
Tracciamo le perpendicolari da quel punto all'asse delle x:

Per la definzione del coseno, essendo \overset{\triangle}{PHO} un triangolo rettangolo, se chiamiamo \alpha l'angolo H\hat{O}P, dobbiamo avere:

\cos(\alpha) = {OH\over OP}

e per la definzione del seno dovremo avere:

\sin(\alpha) = {PH\over OP}

Notiamo quindi che il segmento OP è un raggio e, per costruzione, la circonferenza ha raggio 1, dunque OP è lungo 1.

Per questo, i rapporti delle formule di prima varranno, rispettivamente, la lunghezza di OH e la lunghezza di PH.

State però attenti a non dire che il coseno e il seno sono quei due segmenti. Il seno e il coseno sono definiti come rapporti tra segmenti.

Poi il loro valore è uguale alla lunghezza di quei segmenti, ma ricordatevi che sono rapporti tra segmenti.

Cosa sono, però, la lunghezza di PH e OH? Sono l'ordinata e l'ascissa del punto P!

Quindi, il punto P avrà coordinate (\cos(\alpha) ; \sin(\alpha)):

Quando facciamo il rapporto tra segmenti, dobbiamo prendere le loro lunghezze orientate, perciò otterremo dei valori del coseno e del seno negativi se le coordinate del punto sono negative:

Nel grafico qui sopra, entrambe le coordinate di T sono negative, per questo il coseno e il seno di \beta saranno entrambi negativi.

Quindi, il coseno sarà negativo quando la x del punto è negativa, ovvero nel secondo e terzo quadrante:

Mentre il seno sarà negativo quando la y del punto sarà negativa, cioè nel terzo e nel quarto quadrante:

Ora possiamo dimostrare le cinque relazioni fondamentali della goniometria e definire le altre funzioni goniometriche:

Le cinque relazioni fondamentali della goniometria e le altre funzioni goniometriche

La prima relazione fondamentale già la conoscete benissimo. Essa dice che:

\cos^2(\alpha) + \sin^2(\alpha) = 1

La seconda relazione fondamentale più o meno già la conoscete, ma c'è comunque da aggiungere molto da dire. Essa riguarda la funzione tangente, quindi iniziamo defindendola:

Prendiamo la circonferenza goniometrica e tracciamo la retta x=1, che sarà tangente alla circonferenza nel punto (0;1):

Ora prendiamo un punto P sulla circonferenza goniometrica:

Tracciamo il raggio che congiunge il punto P e tracciamo la retta che lo contiene:

Questa nuova retta intersecherà la retta tangente in un punto T. Chiamiamo poi S il punto di tangenza (1;0).

Definiamo la tangente dell'angolo \alpha come il rapporto tra i segmenti TS e OS:

\tan(\alpha) = {TS\over OS}

Notiamo che OS è un raggio della circonferenza goniometrica, dunque la sua lunghezza dovrà essere uguale ad 1. La lunghezza orientata di TS è uguale all'ordinata di T, dunque la tangente è uguale alla y di T.

Adesso, però, tracciamo la proiezione di P sull'asse delle x:

I triangoli \overset{\triangle}{TSO} e \overset{\triangle}{PHO} sono due triangoli simili, dunque dobbiamo avere:

{TS\over OS} = {PH\over OH}

Possiamo riscrivere PH\over OH come:

{PH\over OH} = {PH \over OH} \cdot {{1\over OP}\over {1\over OP}}= {{PH\over OP}\over {OH\over OP}}

Ricordiamo poi che avevamo definito le funzioni seno e coseno come:

\sin(\alpha) = {PH\over OP}

\cos(\alpha) = {OH\over OP}

Dunque avremo:

{{PH\over OP}\over {OH\over OP}} = {\sin(\alpha)\over \cos(\alpha)}

Quindi:

\tan(\alpha) = {TS\over OS} = {\sin(\alpha)\over \cos(\alpha)}

\tan(\alpha) = {\sin(\alpha)\over \cos(\alpha)}

Cioè, la tangente è il rapporto tra il seno e il coseno. Questa è la seconda relazione fondamentale della goniometria.

Definiamo ora un'altra funzione goniometrica: la cotangente.

Per farlo, prendiamo sempre la circonferenza goniometrica, ma questa volta invece che prendere la retta tangente al punto (1;0), prendiamo quella tangente al punto (0;1).

Facciamo lo stesso procedimento di prima ma con questa retta orizzontale invece che quella verticale:

Definiamo quindi la cotangente di alfa come il rapporto tra i segmenti TS e OS:

\cot(\alpha) = {TS\over OS}

Tracciamo ora la proiezione di P sugli assi cartesiani:

Notiamo che i triangoli \overset{\triangle}{TSO} e \overset{\triangle}{PKO} e dunque dobbiamo avere:

{TS\over OS}= {PK\over KO}

Siccome poi PK = OH e KO = PH, dovremo avere:

{TS\over OS}= {HO\over PH}

Adesso, come prima, possiamo moltiplicare sia il numeratore che il denominatore per {1\over OP}, ottenendo:

{TS\over OS} = {{HO\over OP}\over {PH\over OP}}

Per definizione, abbiamo:

{HO\over OP} = \cos(\alpha)

{PH\over OP} = \sin(\alpha)

Quindi:

{TS\over OS} = {\cos(\alpha)\over \sin(\alpha)}

\cot(\alpha) = {\cos(\alpha)\over \sin(\alpha)}

Cioè la cotangente di alfa è uguale al coseno di alfa fratto il seno di alfa, cioè è il reciproco della tangente:

\cot(\alpha) = {1\over \tan(\alpha)}

Questa era la terza relazione fondamentale della goniometria.

Per passare alla quarta, dobbiamo prima definire la funzione secante:

Prendiamo come sempre la circonferenza goniometrica e riprendiamo la retta tangente ad essa nel punto (1;0):

Effettuiamo lo stesso procedimento per la tangente:

Definiamo quindi la secante di alfa come il rapporto tra i segmenti OT e OS:

\sec(\alpha) = {OT\over OS}

Notiamo che i triangoli \overset{\triangle}{TSO} e \overset{\triangle}{PHO} sono due triangoli simili e dunque dobbiamo avere:

{OT\over OS} = {OP\over OH}

Possiamo riscrivere OP\over OH come {1\over {OH \over OP}}. Siccome per definizione abbiamo \cos(\alpha) = {OH\over OP}, avremo:

{OT\over OS} = {1\over \cos(\alpha)}

\sec(\alpha) = {1\over \cos(\alpha)}

Cioè la secante è il reciproco del coseno. Questa era la quarta relazione fondamentale della goniometria.

Per l'ultima relazione, dobbiamo prima definire la cosecante:

Effettuiamo lo stesso procedimento fatto per definire la cotangente:

Prendiamo la circonferenza goniometrica e la retta ad essa tangente nel punto (0;1):

Definiamo la cosecante di alfa come il rapporto tra i segmenti OT e OS:

\csc(\alpha) = {OT\over OS}

Notiamo di nuovo che i triangoli \overset{\triangle}{TSO} e \overset{\triangle}{PKO} e dunque dovremo avere:

{OT\over OS} = {OP \over OK}

Siccome OK = PH, possiamo riscrivere {OP\over OK} come OP\over PH che a sua volta possiamo riscrivere come 1\over {PH\over OP} e per definizione abbiamo \sin(\alpha) = {PH\over OP}, quindi:

{OT\over OS} = {1\over \sin(\alpha)}

\csc(\alpha) = {1\over \sin(\alpha)}

Cioè la cosecante è uguale al reciproco del seno. Questa era l'ultima delle cinque relazioni fondamentali della goniometria, che dunque ricordiamo essere:

\cos^2(\alpha) + \sin^2(\alpha) = 1

\tan(\alpha) = {\sin(\alpha)\over \cos(\alpha)}

\cot(\alpha) = {\cos(\alpha) \over \sin(\alpha)}

\sec(\alpha) = {1\over \cos(\alpha)}

\csc(\alpha) = {1\over \sin(\alpha)}