Scomposizione in fattori primi
Di seguito analizzeremo la scomposizione in fattori primi.
 Cosa devo già sapere?
Cosa devo già sapere?Teorema fondamentale dell'aritmetica
Prima di vedere la scomposizione in fattori primi, dobbiamo studiare il teorema fondamentale dell'artimetica. Si tratta di un teorema molto importante, sennò non si chiamerebbe fondamentale.
Cosa dice? Esso enuncia che:
Ogni numero naturale non primo si può esprimere come prodotto di numeri primi in maniera univoca (cioè in un solo modo).
Se, invece, il numero in questione è primo, allora la sua scomposizione sarà sè stesso.
Quindi, se prendiamo per esempio 6, possiamo esprimerlo come 2\times 3 ed è l'unico modo per farlo (possiamo ovviamente cambiare l'ordine scrivendo 3 \times 2, ma i fattori sono gli stessi).
Se prendo 12, lo posso riscrivere come 4\times 3, cioè 2^2 \times 3.
Se invece ho un numero primo, come 7, lo lascio così.
Quindi, possiamo scomporre ogni numero naturale in un prodotto di numeri primi, che possono pure essere elevati a certe potenze, come il 2^2 nel caso del 12.
Quando prendo un numero è lo riscrivo in questa forma, si dice che l'ho scomposto in fattori primi.
Ok, ma a che serve? Quando tra poco studierete il minimo comune multiplo e il massimo comune divisore, scomporre i numeri in fattori primi vi farà risolvere gli esercizi molto più velocemente. Quindi adesso dovete imparare bene come si fa, in modo da poter risolvere gli esercizi dei prossimi argomenti.
Manca però una cosa importante da capire: come si fa la scomposizione in fattori primi? Perché adesso abbiamo visto casi semplici, come 6 o 12, dove possiamo trovarla facilmente, ma se devo scomporre 378, come faccio?
Vediamo subito come si fa:
Come trovare la scomposizione in fattori primi di un numero
Continuiamo con il numero di prima, cioè 378.
Dovete innanzitutto scrivere il numero sul vostro foglio. Dopodichè dovete tracciare una lunga riga verticale a destra del numero, come abbiamo fatto qui sotto:
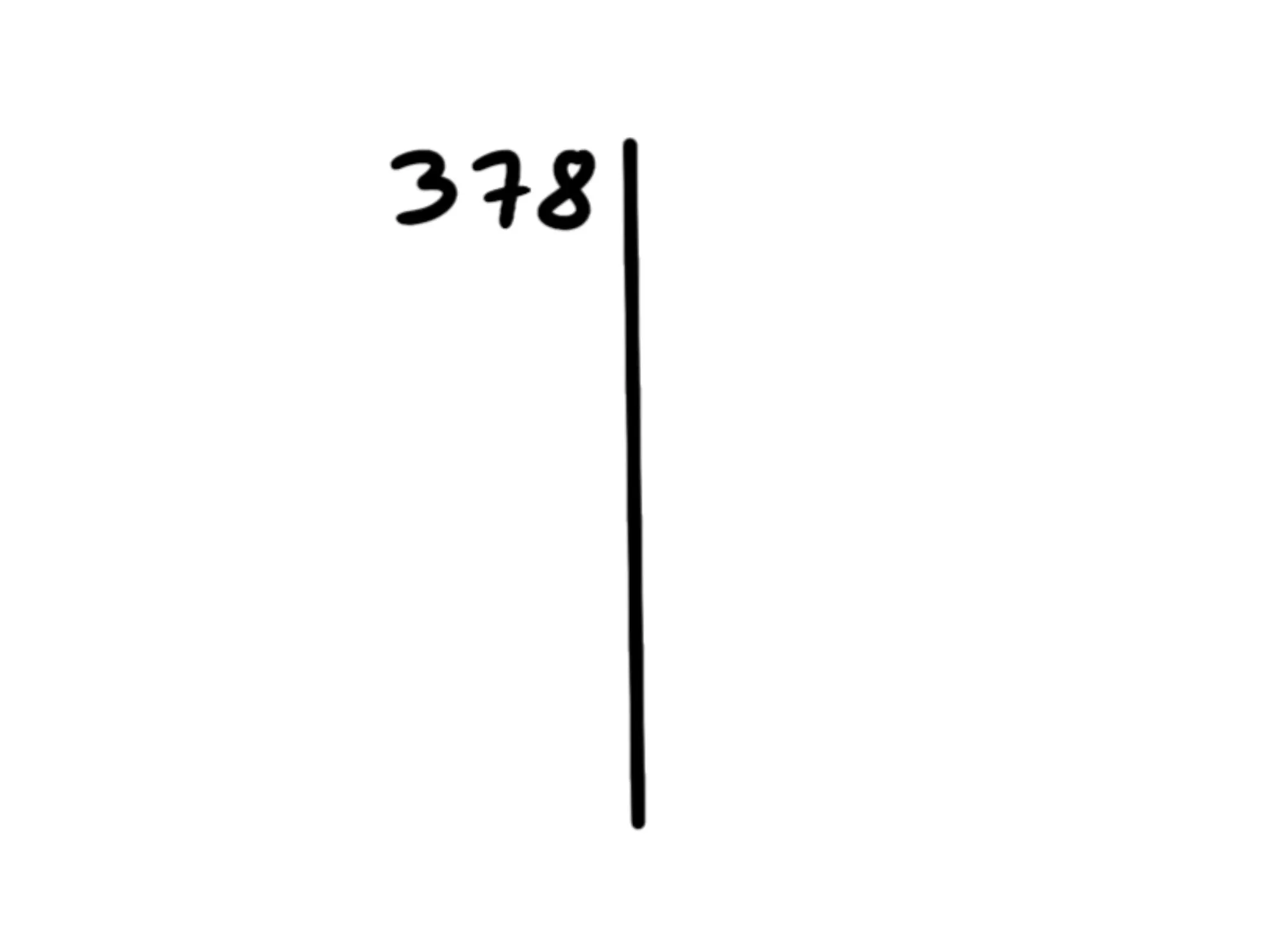
Adesso, usando i criteri di divisibilità, dobbiamo capire per quali numeri primi è divisibile 378. Partiamo dai numeri più piccoli per poi arrivare a quelli più grandi: è divisibile per 2? L'ultima cifra è 8, che è pari, dunque è divisibile per 2.
Ora che sappiamo questo, dividiamo 378 per 2, ottenendo 189. Scriviamo il 2 a destra della riga alla stessa altezza del 378 e scriviamo 189 sotto al 378:
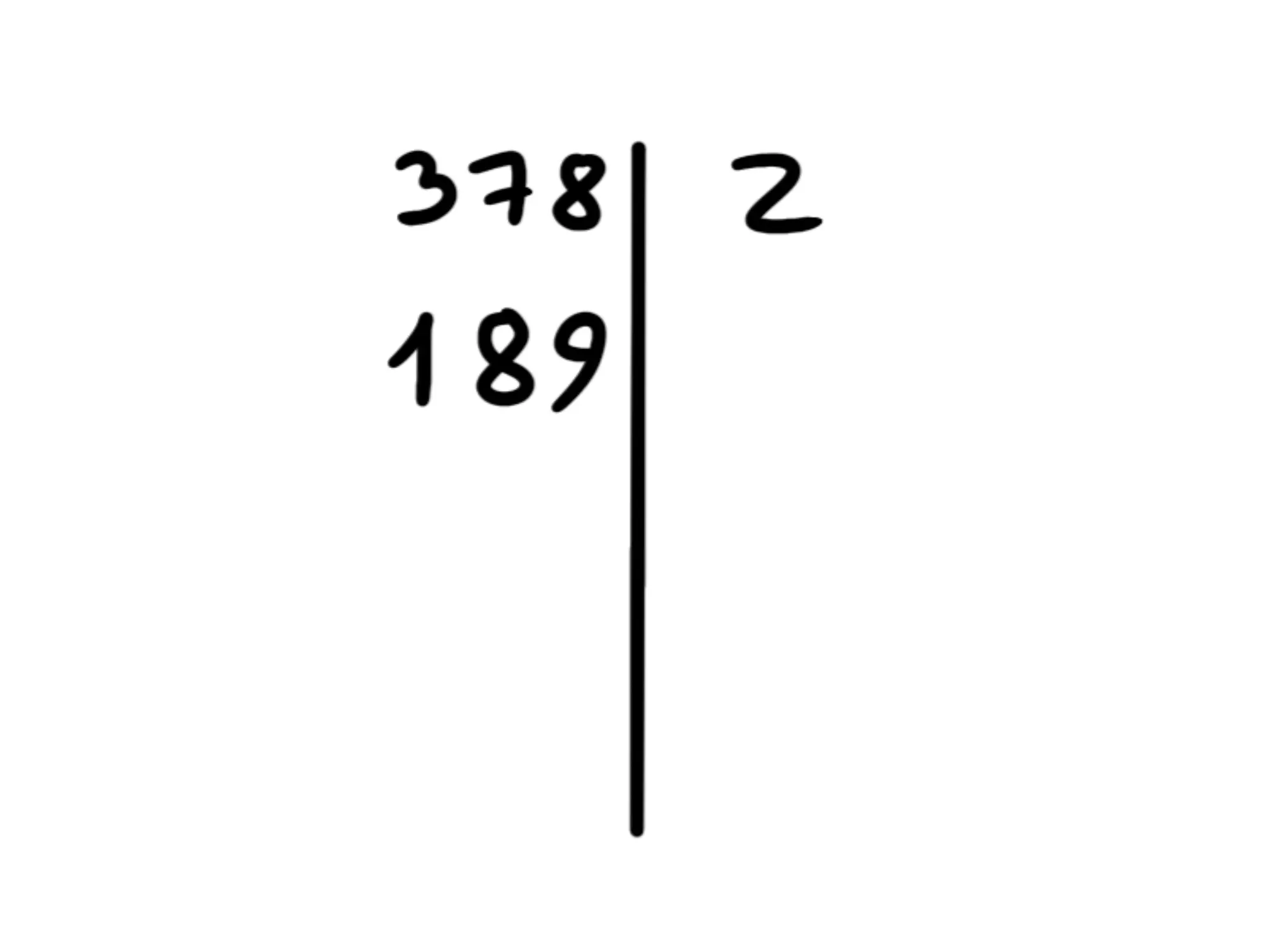
Ora applichiamo lo stesso esatto procedimento a 189: è divisibile per 2? Finisce con 9, che è dispari, quindi no.
Passiamo quindi al prossimo numero primo, cioè 3: è divisibile per 3? La somma delle cifre di 189 fa 18, che è divisibile per 3, dunque 189 è divisibile per 3. Dividiamolo per esso, scriviamo il 3 a destra della riga e mettiamo sotto il risultato della divisione.
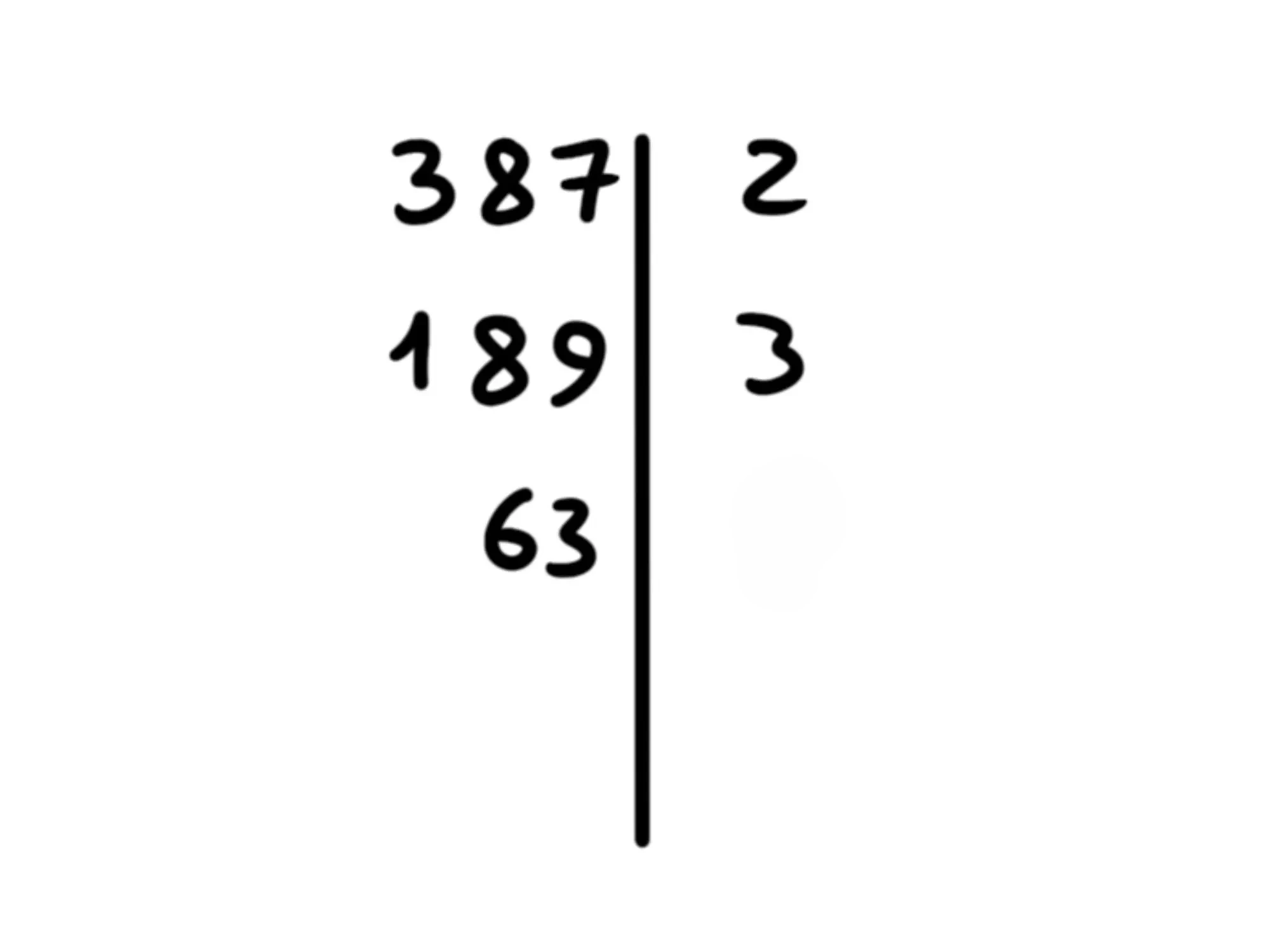
Adesso applichiamo lo stesso procedimento a 63. Però dobbiamo controllare se è divisibile per 2? No, non ce n'è bisogno, perché se 189, che è un suo multiplo, non lo era, nemmeno 63 potrà esserlo. Quindi, non c'è bisogno di ripartire sempre da capo, ma possiamo ripartire direttamente dal numero primo dell'ultima divisione, che in questo caso è 3. Quindi, è divisibile per 3? Sì, allora dividiamo per 3, scriviamo 3 a destra della riga e mettiamo sotto il risultato:
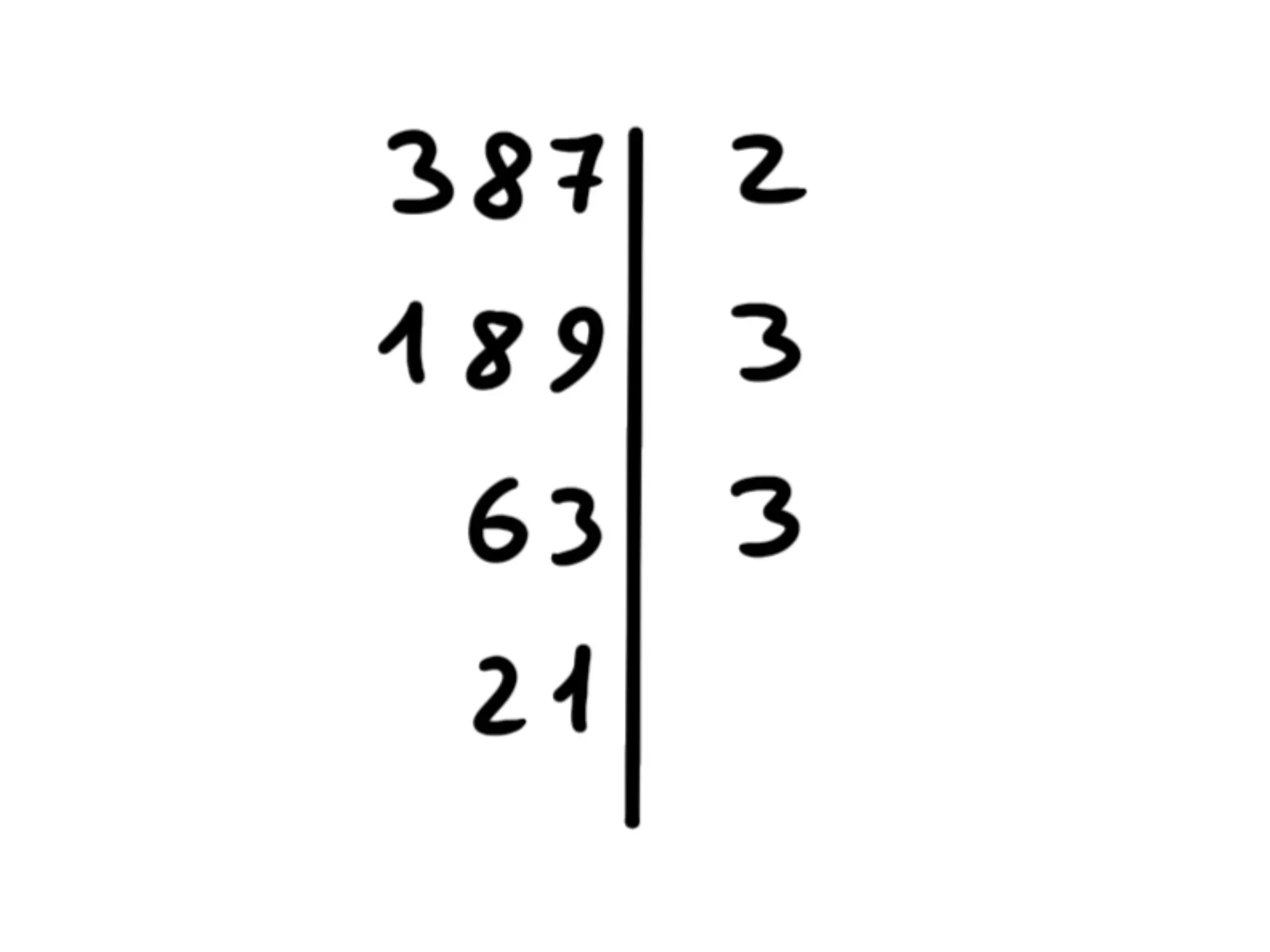
Come avrete capito, dobbiamo ora passare a 21. E' divisibile per 3? Sì, allora dividiamo, mettiamo 3 a destra e il risultato sotto:
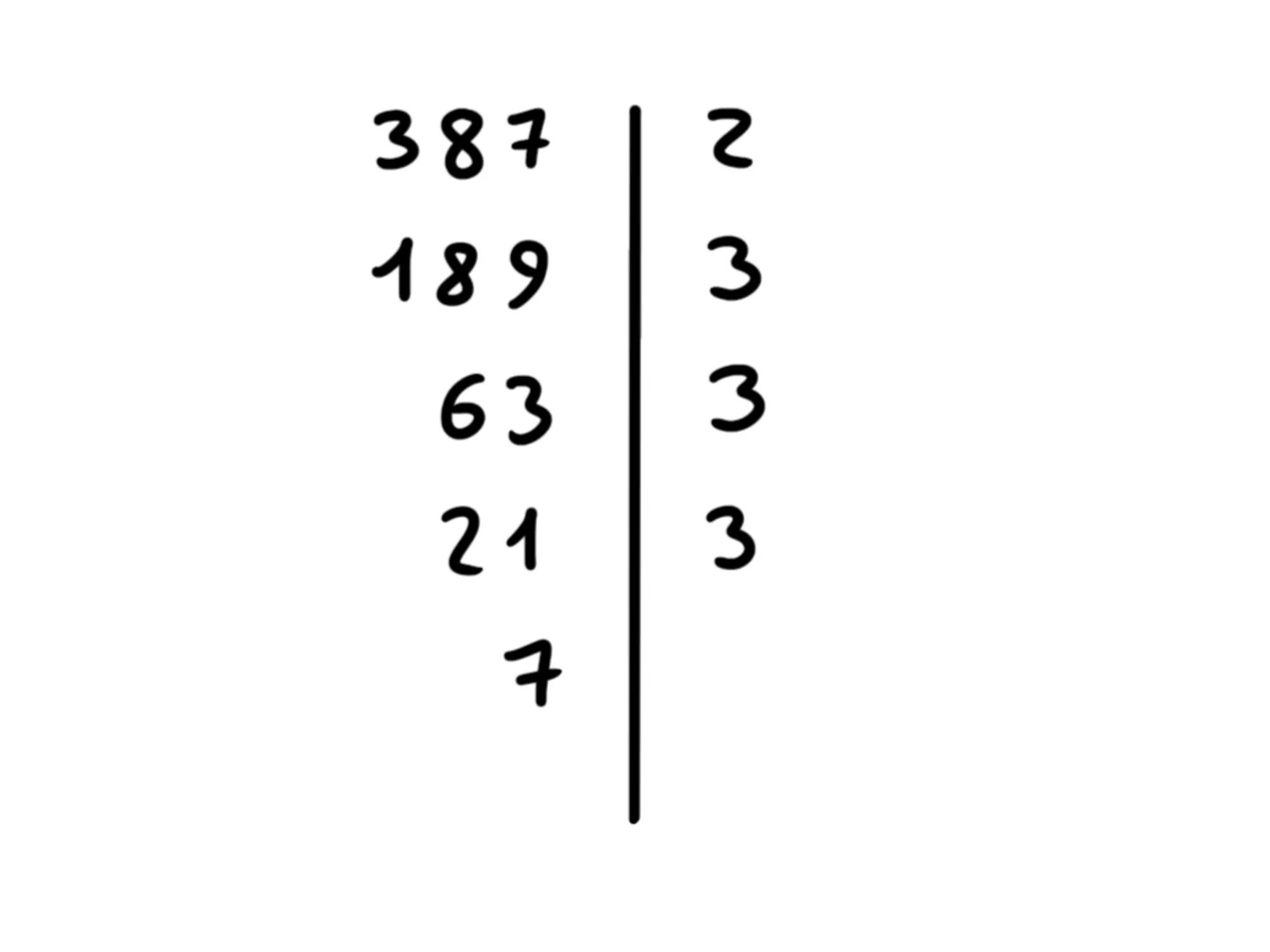
Sappiamo che 7 è un numero primo, quindi sarà solo divisibile per 7. Per questo è inutile mettersi a domandare se è divisibile per 3 o per 5, perché tanto è un numero primo quindi non può esserlo. Diviamo per 7 ed otteniamo finalmente 1:
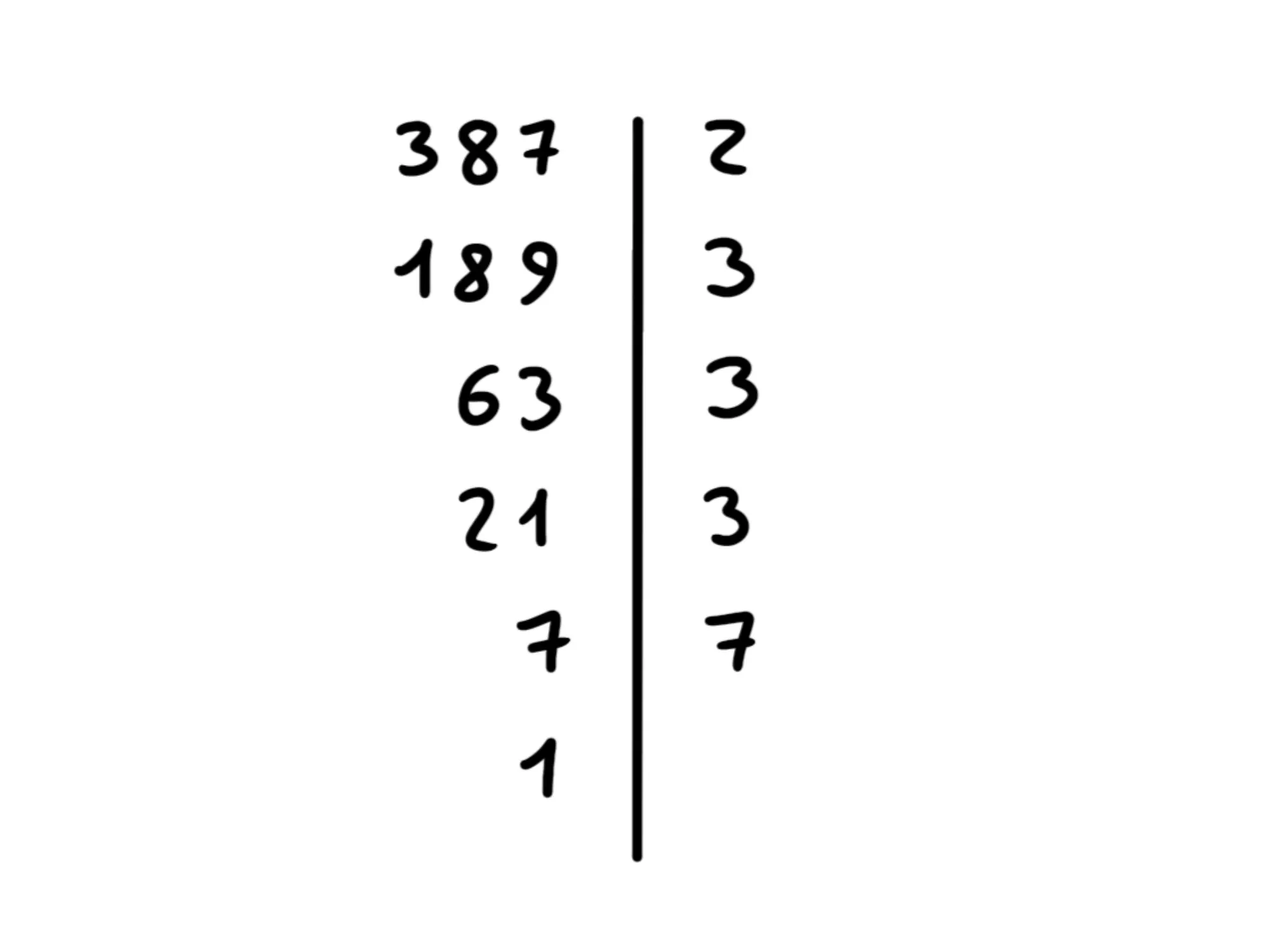
Quando ottenete 1, complimenti! Avete finito la scomposizione. Ora vi basterà prendere i numeri primi che si trovano a destra partendo dall'alto e moltiplicarli tra loro. Per fare più velocemente, potete direttamente scrivere ogni numero primo una sola volta e mettergli come esponente il numero delle volte che lo trovate, perché moltiplicare n volte un numero per sè stesso è uguale, per definizione, ad elevarlo alla n.
Quindi nel nostro caso abbiamo incontrato 2, 3 e 7. Il 2 compare una sola volta, il 3 compare 3 volte e il 7 solo una volta. La scomposizione in fattori primi sarà dunque 2\times 3^3 \times 7 (abbiamo messo 2 e 7 e non 2^1 e 7^1 perché tanto elevare alla prima non fa niente).
Perciò dobbiamo avere:
378 = 2\times 3^3 \times 7
Può sembrare un processo molto lungo, ma tranquilli, dopo aver fatto molti esercizi diventerete così bravi che li farete super velocemente.
