Integrali
Di seguito analizzeremo gli integrali definiti ed indefiniti. Infine vedremo pure delle loro proprietà e dei metodi per calcolarli.
Cosa devo già sapere?
Prendiamo una funzione qualsiasi:
Prendimao ora due valori a e b sull'asse delle x ed usiamoli per delimitare un pezzo della nostra funzione:
Quello che noi vogliamo sapere è quanto vale l'area di questa regione che abbiamo delimitato:
Questa regione viene chiamata il sottografico della funzione. Noi vogliamo quindi calcolare la sua area. Come fare?
Intanto, possiamo approssimarla con il seguente rettangolo:
Non è mailissimo, ma non è nemmeno una buona approssimazione. Proviamo a prendere un punto tra a e b per creare due rettangoli:
Sembra un pochino meglio. Proviamo quindi a prendere ancora più punti tra a e b:
Molto meglio. Quello che stiamo facendo, infatti, è dividere il nostro intervallo in pezzetti sempre più piccoli. Se i pezzi sono sufficientemente piccoli, la funzione rimane quasi costante in quell'intervallo, quindi un rettangolo approssima bene l'area delimitata da essi:
Più sono piccoli i nostri intervalli e più la funzione è approssimabile come costante in essi. Ci sarà però sempre un po' di differenza. Se però rendiamo i nostri intervalli infinitamente piccoli è come se prendessimo un punto sulla funzione e poi immeditamente il successivo, quindi l'approssimazione diventa così precisa che possiamo ritenerla un'uguaglianza a tutti gli effetti.
Rimane però un problema: come calcolare l'area di tutti questi rettangoli? Cioè, abbiamo appena detto che se dividiamo l'intervallo in pezzetti infinitamente piccoli, possiamo calcolare l'area come la somma di tutte le aree dei rettangoli ottenuti, ma come trovare le aree di tutti questi piccoli rettangoli?
Un modo può essere fare degli intervalli piccoli e calcolare le aree dei rettangoli una per una e sommarle. Quindi prendere intervalli ancora più piccoli e ripetere il processo. Però questo metodo non è buono per due motivi:
Il primo è che ti ci vuole una vita, il secondo è che per quanto tu possa disegnare piccoli gli intervalli, non saranno mai infinitamente piccoli e quindi otterrai solo un'approssimazione. Forse molto buona, ma non sarà mai esattamente uguale all'area del sottografico.
L'unico modo è utilizzare altra matematica. Scriviamo quindi in matematichese la nostra affermazione:
Chiamiamo l'area del sottografico A. L'area di un rettangolo è uguale alla base per l'altezza. La base è la differenza dei valori delle x, che chiameremo quindi \Delta x, mentre l'altezza equivale al valore della funzione:
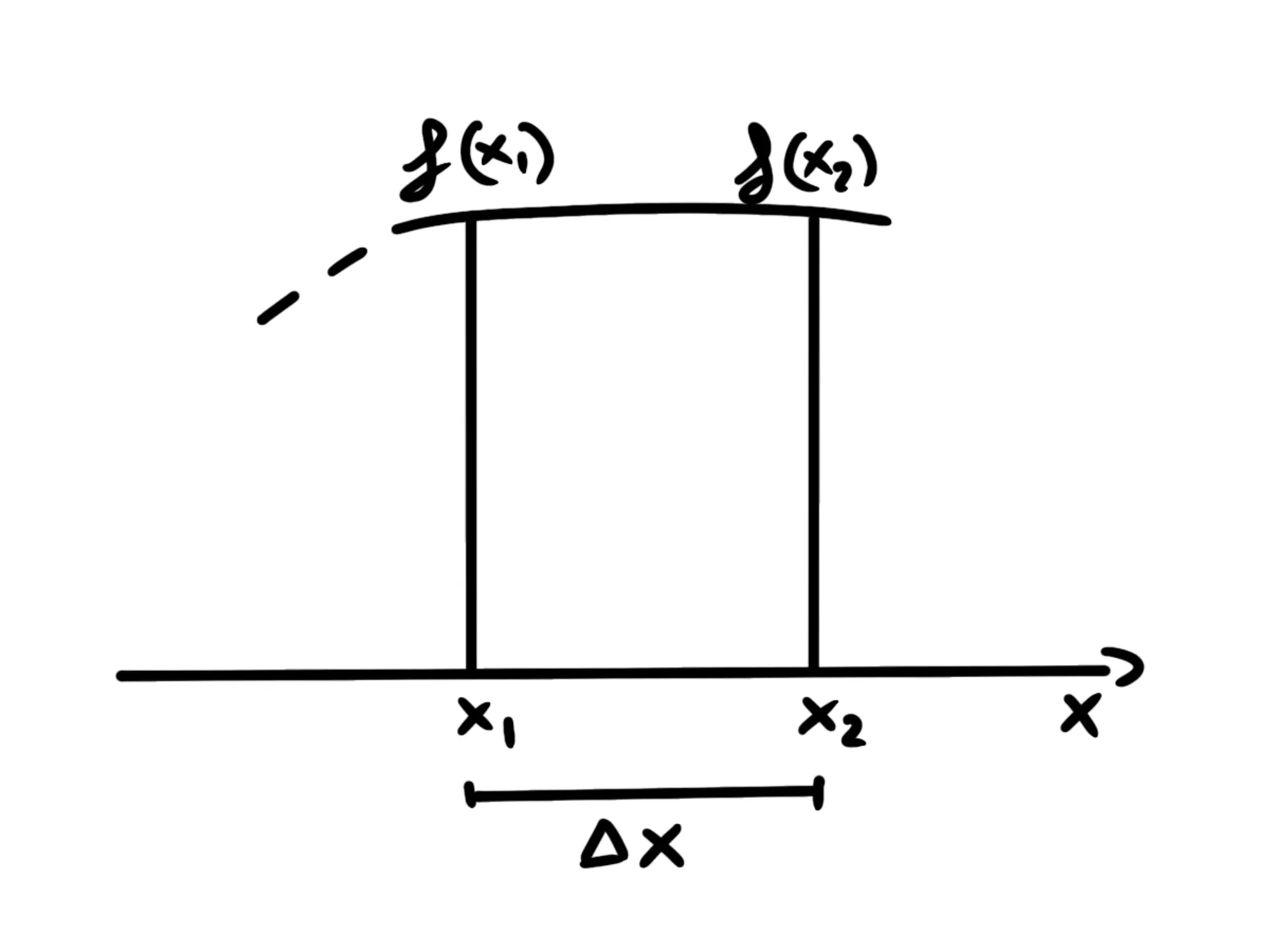
Però, quale dei due valori dobbiamo prendere come altezza? f(x_1) o f(x_2)? In realtà, non importa, perché, come abbiamo detto prima, quando andremo a prendere intervalli infinitamente piccoli, la funzione sarà praticamente costante in quell'intervallo, quindi f(x_1) e f(x_2) saranno uguali.
Dunque avremo:
A \approx f(x_0) \Delta x + f(x_1) \Delta x + ... f(x_n) \Delta x
Dove n è il numero di pezzetti in cui dividiamo l'intervallo. Possiamo usare la notazione con \sum per rendere l'espressione più compatta. Se supponiamo di prendere pezzettini tutti uguali, i \Delta x di ogni rettangolo saranno uguali, dunque non c'è bisogno di mettergli un indice perché non variano da pezzetto in pezzetto:
A \approx \sum_{i=0}^{n} f(x_i) \Delta x
Studiamo però ora un pò meglio questo \Delta x:
Se infatti abbiamo n pezzettini e la lunghezza di tutto l'intervallo vale b-a, avremo che la lunghezza \Delta x di ogni pezzettino sarà:
\Delta x = {b-a \over n}
Quindi, quando andiamo a prendere il limite per n che tende ad infinito, è vero che sommiamo un numero infiniti di termini, ma saranno estremamente piccoli grazie a \Delta x che sta a moltiplicare.
Geometricamente, quando andiamo ad aumentare il numero di rettangoli n è vero che sommiamo più aree, ma quest'ultime sono più piccole.
Dunque, per ottenere il valore esatto dell'area A ci basta prendere il limite per n che tende ad infinito:
A = \displaystyle \lim_{n\to +\infty} \sum_{i=0}^{n} f(x_i) \Delta x
Siccome \Delta x diventa un'infinitesimale, come abbiamo fatto per le derivate, lo andiamo a scrivere come dx. Per questa somma di infiniti rettangoli molto piccoli, esiste una notazione più comoda:
A= \int_{a}^{b} f(x) dx
Quella curva strana sarebbe una S scritta all'antica e sta per "summa", ovvero "somma", perché è quello che stiamo facendo. Sotto questa S scriviamo il punto di partenza e sopra il punto di arrivo. Dopo scriviamo cosa dobbiamo sommare, in questo caso l'area dei rettangoli. Questa nuovo oggetto matematico viene chiamato l'integrale definito da a a b di f(x). a e b vengono chiamati gli estremi di integrazione.
Ok, abbiamo trovato questa notazione carina per indicare l'area del sottografico di A, ma qual'è il punto? Come facciamo a calcolare l'area A, visto che era quello il nostro obbiettivo?
Il punto di aver fatto tutto ciò è che esiste un metodo per calcolare un'integrale:
Prendiamo quindi l'integrale da a a b di una funzione f(x):
\int_{a}^{b} f(x) dx
Ora prendiamo una funzione F(x) tale che:
F'(x)=f(x)
Cioè, la sua derivata deve essere uguale alla nostra funzione f(x). Se questa condizione è verificata, allora il teorema fondamentale del calcolo integrale ci dice che:
\int_{a}^{b} f(x) dx = F(b) - F(a)
Quindi, quello che dobbiamo fare è trovare l'antiderivata di f(x) (talvolta chiamata la primitiva di f(x)) e fare la differenza tra questa funzione applicata ai due estremi di integrazione.
Come trovare l'antiderivata? A volte può essere molto complicato, ma esistono varie tecniche che studieremo nella loro sezione apposita.
Vediamo quindi finalmente un esempio di come trovare l'area del sottografico:
Prendiamo la funzione f(x)=-3x^2 e calcoliamo l'area del suo sottografico tra 1 e 3. Per quello che abbiamo detto prima, avremo che:
A= \int_{1}^{3} (-3x^2) dx
Si mette la funzione per dx tra parentesi per indicare cosa si sta integrando, però normalmente, se è sottinteso, si tolgono.
Troviamo quindi l'antiderivata di -3x^2. Si può notare facilmente che si tratta di -x^3. Possiamo quindi trovare il valore dell'area:
A= \int_{1}^{3} -3x^2 dx = F(3) - F(1) = (-(3)^3) - (-(1)^3) = -27 +1 = -26
-26? Come fa un'area ad essere negativa? Quella che calcola l'integrale, infatti, è l'area orientata del sottografico. Cioè, se è sopra l'asse x è positiva, se è sotto l'asse x è negativa. Infatti, il grafico della nostra funzione è la seguente parabola:
Per questo ci è uscito un valore negativo. Per questa ragione, l'area orientata del seguente sottografico vale 0:
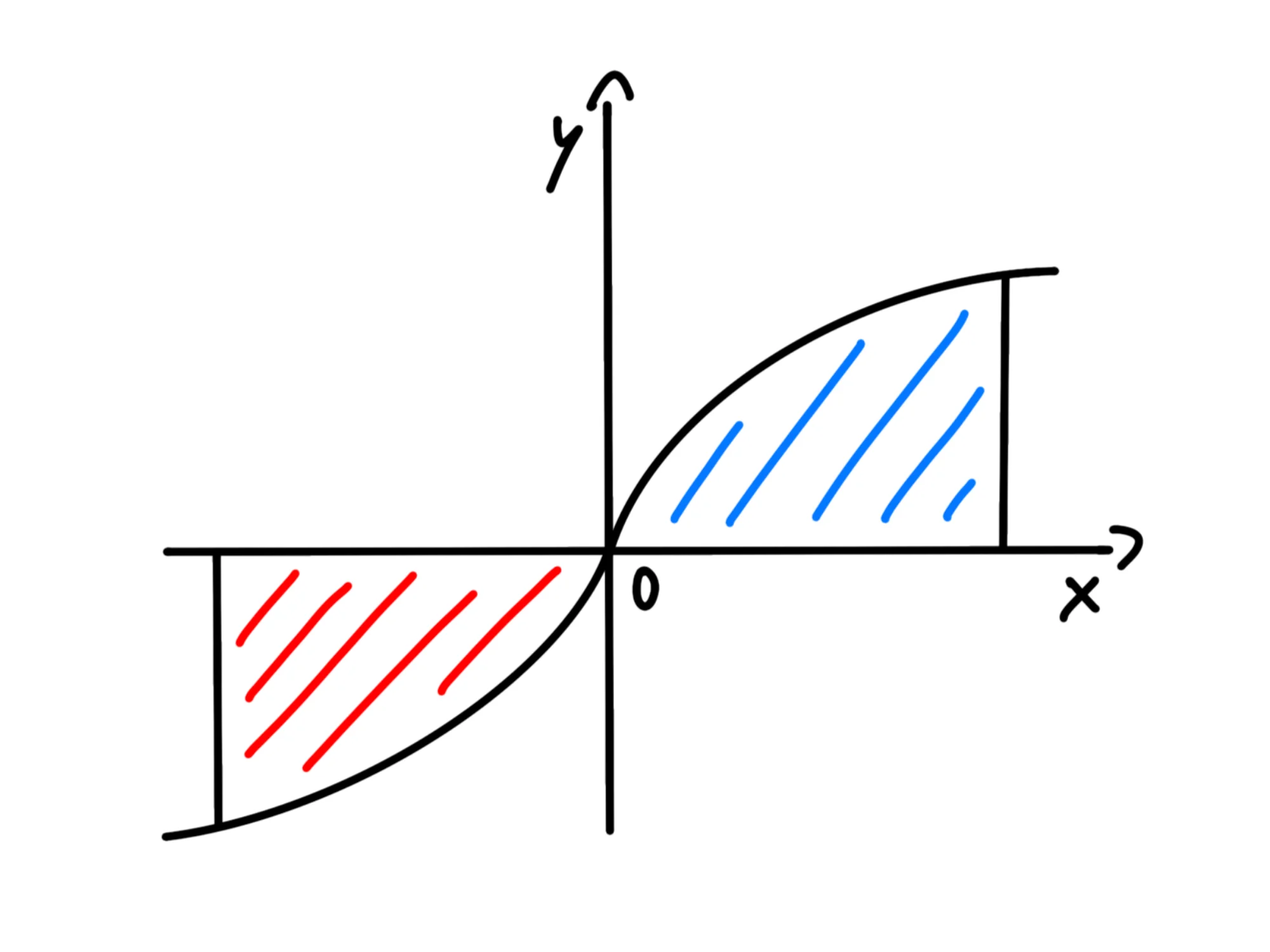
Siccome si tratta dell'area orientata, l'area di sopra si semplifica con l'area negativa di sotto ed otteniamo 0.
Per semplificare la scrittura, quando andiamo a calcolare la differenza dell'antiderivata nei due estremi di integrazione, lo scriviamo nel seguente modo:
F(b)-F(a) = F(x) |_{a}^{b}
In questo modo possiamo scriverci l'antiderivata e poi sostituire, senza fare troppi passaggi in una volta sola.
La difficoltà nel lavorare con gli integrali risiede nel 99 \% dei casi nel trovare l'antiderivata.
Infatti, mentre usando le proprietà delle derivate possiamo calcolare la derivata di qualsiasi funzione, pure complicatissima, per gli integrali, invece, esistono solo dei metodi che qualche volta ti permettono di semplificare un po'. Però non preoccupatevi, proprio per questo vi verranno presentati solo integrali di funzioni piuttosto semplici.
Prima di studiare le proprietà degli integrali, introduciamo gli integrali indefiniti:
Integrali indefiniti
Nel risolvere gli integrali definiti, il punto cruciale risiede nella ricerca dell'antiderivata. Per questo, possiamo astrarre l'idea di integrale ad un integrale indefinito. Ovvero, non ci importa più trovare l'area del sottografico, ma ci importa solo trovare l'antiderivata. Non ci sarà dunque nemmeno bisogno di indicare gli estremi di integrazione:
\int f(x) dx = F(x)
Quindi, qual'è la differenza tra un integrale definito e un integrale indefinito? Che l'integrale definito ci da come risultato un numero, corrispondente all'area orientata del sottografico della funzione, mentre l'integrale indefinito ci da come risultato l'antiderivata della funzione che stiamo integrando.
Dunque, in entrambi i casi si cerca l'antiderivata della funzione, ma nel primo caso otteniamo un numero, nel secondo una funzione.
Vediamo quindi un esempio di integrale indefinito. Risolviamo il segunte integrale:
\int 2x dx
Si nota facilmente che l'antiderivata di 2x è uguale a x^2. Otteniamo quindi:
\int 2x dx= x^2
Finito qui? No, questo è uno degli errori più comuni. Non bisogna fermarsi qui, c'è ancora uno step. Infatti, l'integrale definito non ci da come risultato un'antiderivata della nostra funzione, ma ci da tutte le antiderivate della nostra funzione.
Ce ne sono altre? Se vi ricordate, la derivata di una costante è sempre 0 e la derivata di una somma è uguale alla somma delle derivate.
Dunque, anche x^2 + 4 è un'antiderivata di 2x, anche x^2 -10, x^2+19, x^2-1... sono tutte antiderivate di 2x. Dunque dobbiamo andare a sommare una generica costante C al risultato:
\int_{a}^{b} 2x dx = x^2 + C
Fate attenzione perché questa quasi tutti la sbagliano di tanto in tanto.
Per questa ragione, poi, sentirete dire che l'integrale indefinito da come risultato una famiglia di funzioni. Perché, aggiungendo una costante C, otteniamo un numero infinito di funzioni come risultato.
Perché prima, allora, quando studiavamo gli integrali definiti, non abbiamo messo +C? Perché quando andiamo a calcolare la differenza, le due costanti si semplificherebbero. Dunque lì non importavano, però non mettere +C nel risultato di un integrale indefinito è un errore grave.
Vediamo ora qualche tecnica per la risoluzione degli integrali indefiniti (che ci permetteranno quindi, poi, di risolvere pure gli integrali definiti):
Proprietà degli integrali e metodi di risoluzione
Iniziamo con qualche proprietà molto intuitiva:
Invertire gli estremi di integrazione cambia il segno dell'integrale:
\int_{a}^{b} f(x) dx = -\int_{b}^{a} f(x) dx
Questo perché il primo è uguale a F(b)- F(a) e moltiplicando per -1 otteniamo F(a)-F(b), che è infatti l'integrale con gli estremi di integrazione invertiti.
Un integrale definito con estremi di integrazione uguali vale sempre 0:
\int_{a}^{a} f(x) dx = 0
Infatti, se partiamo da a per rimanere fermi ad a, non delimitiamo alcuna area.
Proprietà di additività rispetto agli estremi:
\int_{a}^{b} f(x) dx + \int_{b}^{c} f(x) = \int_{a}^{c} f(x) dx
Questo perché se calcoliamo separatamente le due aree orientate e le sommiamo o se calcoliamo tutta l'area in una sola volta, non cambia niente:
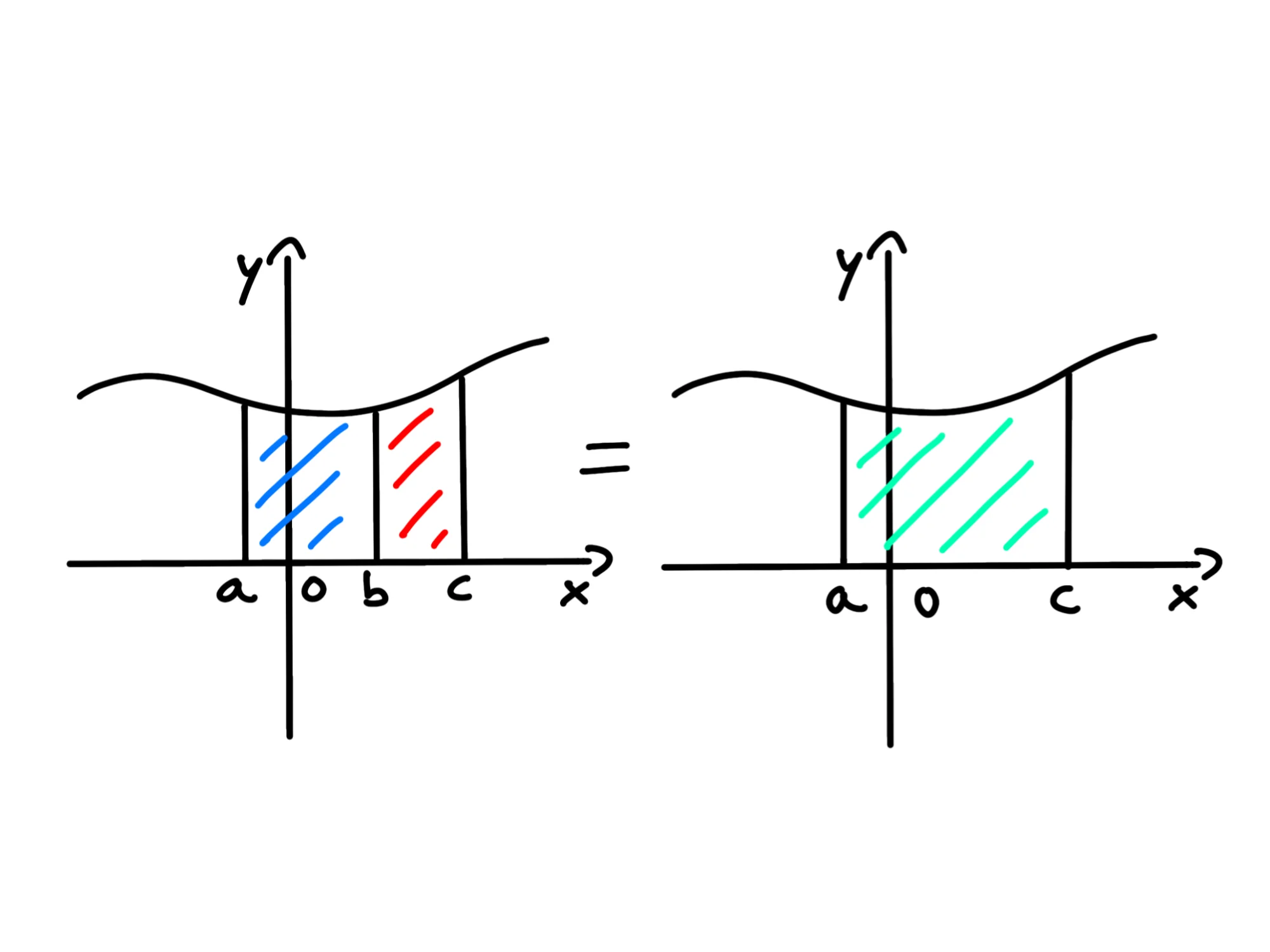
Passiamo ora a delle proprietà più interessanti. Come per la derivata, l'integrale di una somma equivale alla somma degli integrali (questo vale sia per i definiti che per gli indefiniti):
\int_{a}^{b} (f(x) + g(x) dx) = \int_{a}^{b} f(x) dx + \int_{a}^{b} g(x) dx
Anche l'integrale (definito o indefinito) di una funzione per uno scalare equivale allo scalare per l'integrale:
\int_{a}^{b} d\cdot f(x) dx = d\cdot \int_{a}^{b} f(x) dx
Con queste formule potrete calcolare l'integrale di qualsiasi funzione polinomiale. Infatti, applicando la regola della potenza, ottenete che siccome:
{d\over dx} x^n = n x^{n-1}
Allora dobbiamo avere:
x^n + C = \int n x^{n-1}
\int x^{n-1} = {x^n \over n} +C'
Abbiamo chiamato C\over n come C'. Siccome si tratta di costanti generiche, è comune infatti richiamarle in una altro modo per abbreviare, perché tanto rimane comunque una costante generica.
Dunque, se al posto di n-1 mettiamo n, otteniamo:
\int x^{n} ={x^{n+1}\over n+1} + C
Quindi vi basterà dividere i vari termini della funzione polinomiale, portare fuori dall'integrale i coefficienti e usare questa nuova formula per ogni termine.
E per l'integrale di un prodotto? Al contrario della derivata, non esiste una formula che ci permette di esprimere l'integrale di un prodotto in funzione degli integrali dei singoli fattori. Abbiamo, però, quella che viene chiamata la tecnica di integrazione per parti:
Se abbiamo un integrale indefinito del seguente tipo:
\int f(x)\cdot g'(x) dx
Con la tecnica dell'integrazione per parti possiamo riscriverlo come:
\int f(x)g'(x) dx = f(x) g(x) - \int f'(x)g(x) dx
Quindi, ad esempio, se abbiamo l'integrale indefinito:
\int xe^x dx
Possiamo scegliere f(x)=x e g'(x)=e^x (e quindi g(x) = e^x) ed ottenere:
\int xe^x dx = xe^x - \int 1\cdot e^x dx = xe^x - e^x +C
Ed ecco risolto l'integrale. Vediamo quindi l'ultima tecnica di questa lezione.
Possiamo infatti sostituire la nostra variabile di integrazione x con un altra variabile u.
Dovremo avere una qualche relazione tra x ed u:
u=g(x)
Dunque avremo:
du = g'(x) dx
Isolando dx otteniamo:
dx = {du\over g'(x)}
Nel caso dell'integrale indefinito, ci basterà sostiuire le g(x) con u e sostituire {du\over g'(x)} al posto di dx.
Ovviamente, dovremo scegliere una buona g(x) affinchè l'integrale si semplifichi. Vediamo un esempio. Risolviamo il segunte integrale indefinito:
\int {1\over x^2 + 2x + 1} dx
Notiamo che al denominatore abbiamo un quadrato perfetto. Raccogliamolo:
\int {1\over (x+1)^2} dx
Se al posto di {1\over (x+1)^2} avessi {1\over x^2}, potrei riscriverlo come x^{-2} e applicare la regola della potenza al contrario. Come fare? Posso sostituire u= x+1.
Dunque, du =g'(x) dx e in questo caso g(x)=x+1, quindi g'(x)=1, e l'equazione diventa du=dx.
Ora ci basta sostituire u al posto di x+1:
\int {1\over u^2} du
Dunque otteniamo:
\int u^{-2} du = {u^{-1} \over -1} +C = -{1\over u} + C
Risostitutiamo x per ottenere:
-{1\over x+1} +C
Quindi abbiamo ottenuto che:
\int {1\over x^2 + 2x +1} dx = -{1\over x+1} +C
Qualche volta, invece di voler scrivere la nuova variabile u in funzione di x, ci capiterà di voler scriver x in funzione di u. Il procedimento sarà più o meno lo stesso, ma avremo:
x=s(u), quindi dx = s'(u)du e sostituiremo s(u) al posto di ogni x.
Infine, nel caso di un integrale definito? Il procedimento iniziale è lo stesso, ma dobbiamo considerare gli estremi di integrazione.
Se effettuiamo una sostituzione del tipo u=g(x), ci basterà sostituire a con g(a) e b con g(b).
Se invece effettuiamo una sostituzione del tipo x=s(u), al posto di a metteremo s^{-1}(a) e al posto di b metteremo s^{-1}(b).
Con questi metodi dovreste essere capaci di risolvere tutti gli integrali che vi verranno proposti. Se infatti è vero che alcuni integrali non possono essere risolti con questi metodi, non ne incontrerete di questo genere al liceo.