Limite di una funzione

Cosa devo già sapere?

Da sapere:

Funzioni

Cosa sono i limiti?

Il limite è uno strumento che ci permette di studiare il valore di una funzione quando ci si avvicina sempre di più a un punto specifico.

Può capitare di voler studiare una funzione a un valore a. Può però anche capitare che, per qualche ragione, non possiamo calcolare il valore di f(a) o non ci conviene farlo. Però, grazie ai limiti, possiamo vedere come si comporta la funzione quando si avvicina molto ad a.

Vediamo questo concetto in un caso molto semplice. Prendiamo la parabola di equazione y=x^2 + 2 e supponiamo di voler sapere quanto vale la funzione quando la x è uguale a 3.

In questo caso basterebbe sostituire 3 al posto della x, ma vediamo come possiamo usare il concetto di limite per farlo. In questo modo, quando nel prossimo esempio saremo costretti ad usare un limite, il processo vi apparirà più chiaro.

Quindi abbiamo detto che vogliamo calcolare f(3) usando valori della x molto vicini. Prendiamo per esempio f(2), che è uguale a 6:

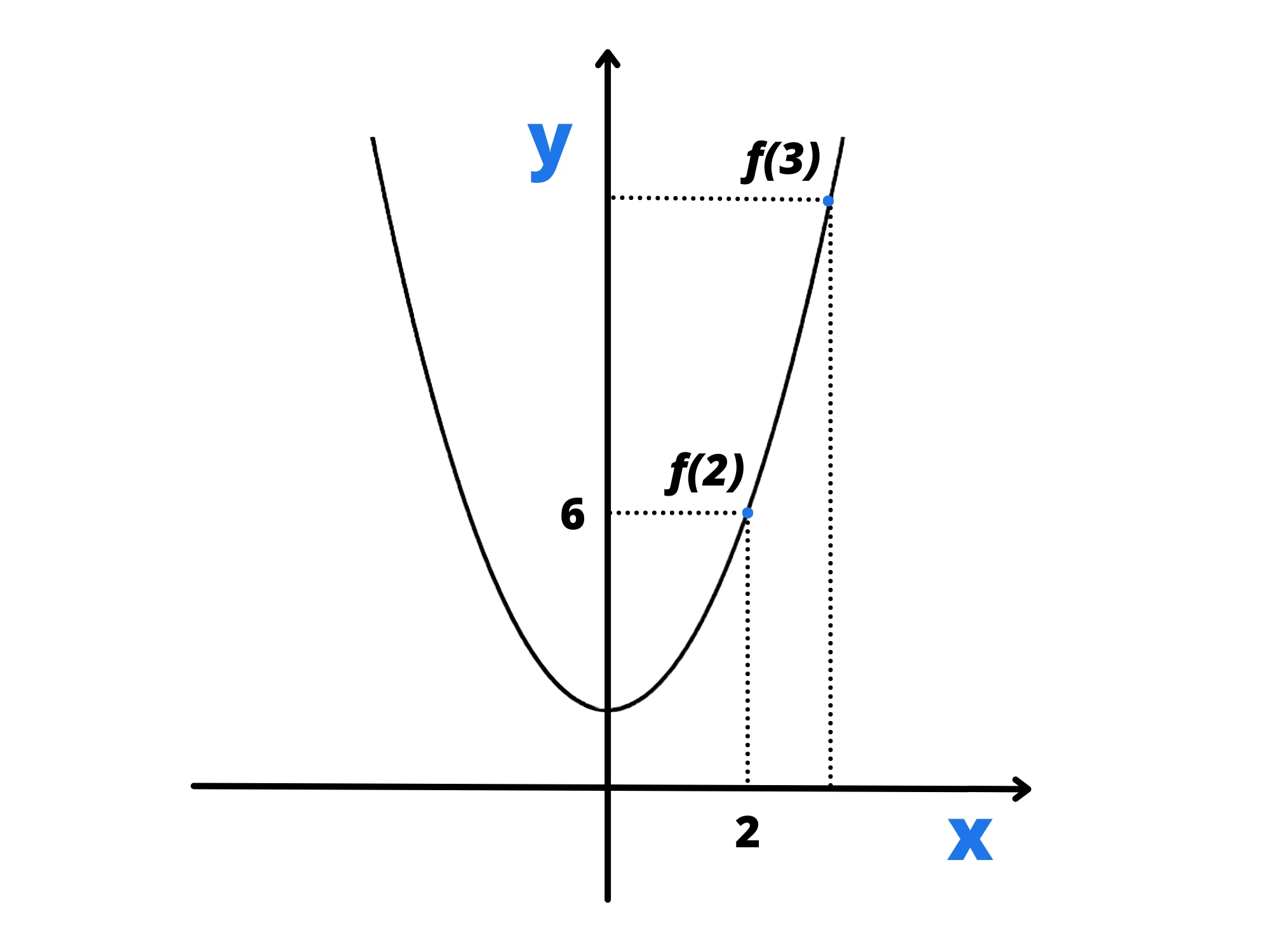
Non siamo troppo lontani, ma possiamo fare decisamente di meglio. Prendiamo f(2.9), che sarebbe uguale a 10,41.

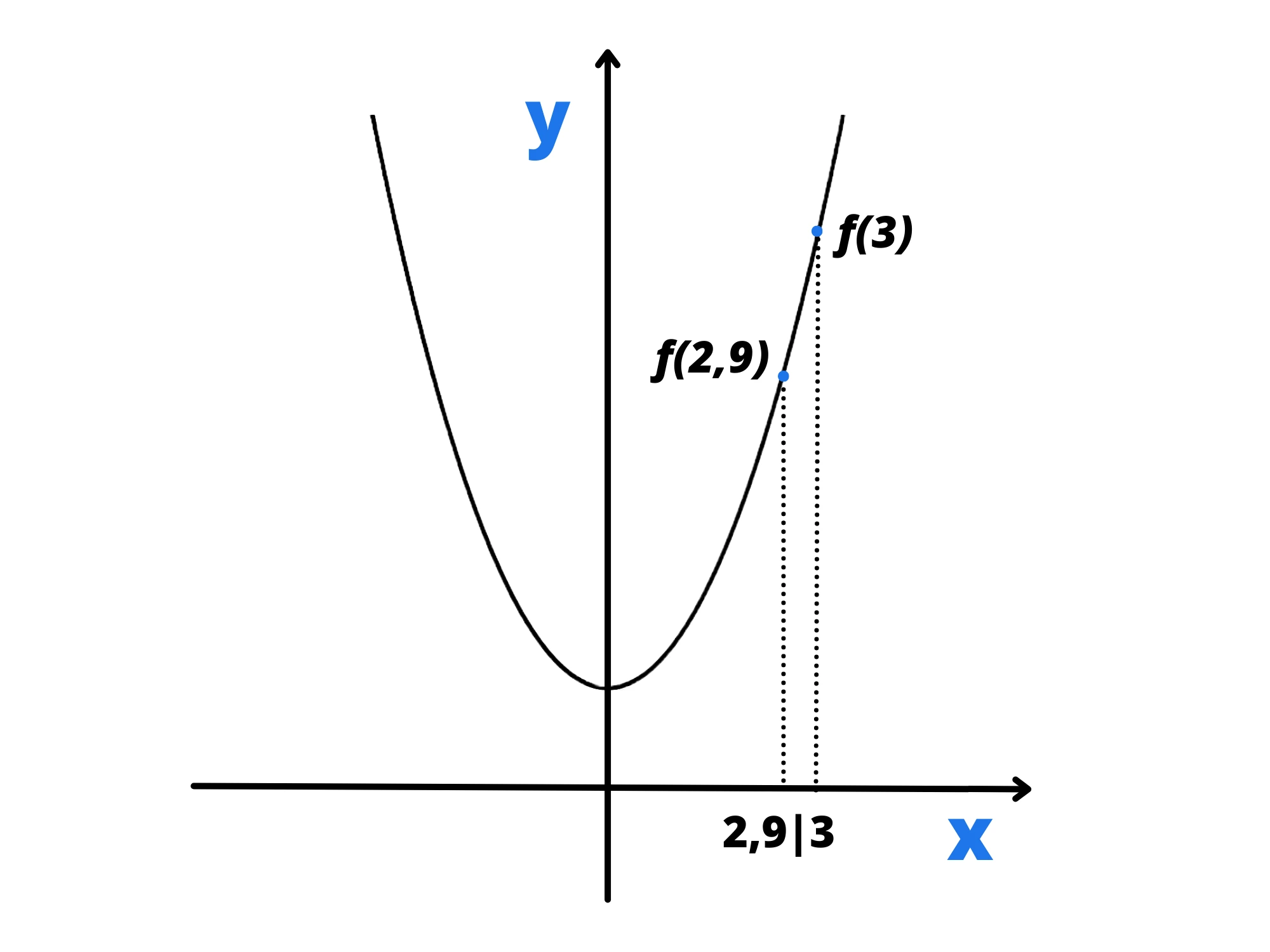
Possiamo fare ancora meglio, prendiamo f(2.999). Ad occhio nudo sono così vicini i valori che sembrano essere uguali, però ancora non lo sono. Sappiamo infatti che f(3)=11, mentre f(2.999)=10,994001. Se infatti ingrandiamo il grafico possiamo notare bene la differenza:

Possiamo però continuare questo processo ed avvicinarci sempre di più. Più mettiamo numeri vicini e più si avvicina ad 11, ma non lo toccherà mai veramente. Arriverà a 10.9999999999... con infiniti 9, ma non raggiungerà mai 11, è il suo limite, deve stare appena appena di sotto.

Dunque ora dovrebbe apparire chiara la definzione di limite di una funzione. "Il limite di una funzione f(x) per x che tende ad un valore a, è quel valore a cui tende f(x) quando x, appunto, tende a a".

Con il verbo "tendere" si intende proprio che la funzione si avvicina a quel valore sempre di più. Questa definizione che abbiamo dato non è molto rigorosa e forse qualcuno la chiamerebbe imprecisa, ma l'obbiettivo di questa lezione è solo dare un'idea intuitiva di cosa sia un limite. Parleremo più dettagliatamente dei limiti in altre lezioni.

Vediamo quindi la notazione da usare per un limite: scriviamo "lim" e sotto di esso scriviamo il nome della variabile (solitamente x) con una freccia che indica il valore a cui tende. Infine scriviamo la funzione di cui prendiamo il limite:

\displaystyle \lim_{x \to a} f(x)

Nel nostro esempio di prima, quindi, avremo:

\displaystyle \lim_{x \to 3} (x^2 +2) = 11

Abbiamo messo delle parentesi intorno alla funzione, ma solitamente si sottintendono. Dunque, ricapitolando, il limite di x^2 +2 per x che tende a 3 è uguale a 11 perché quando la x si avvicina sempre di più a 3, la nostra funzione si avvicina sempre di più a 11.

Adesso, però, viene spontaneo chiedersi perché usare i limiti. Non potevamo direttamente sostituire 3 nell'equazione è finirla là? In quel caso sì, ma vediamo un altro esempio in cui invece è fondamentale usare i limiti.

Prendiamo f(x)={x^2 \over x}. Se la disegnamo notiamo che assomiglia molto alla retta di equazione y=x:

Però c'è un'importante differenza, la nostra funzione non è definita ad x=0. Infatti, per x \neq 0 la frazione si semplifica ed otteniamo f(x)=x, ma nel caso x=0 otteniamo:

f(0)={0^2 \over 0}

E come sappiamo, frazioni del tipo {0\over 0} sono indeterminate. Quindi, come facciamo a sapere come si comporta quando x tende a 0? Adesso noi abbiamo già visto il suo grafico, quindi già sappiamo come si comporta, ma in generale è molto difficile predire l'andamento di una funzione in un punto critico come questo e l'unico modo per scoprirlo è usare un limite.

Risolviamo ora il nostro esempio, noi vogliamo trovare quanto vale \displaystyle \lim_{x \to 0} f(x), ovvero:

\displaystyle \lim_{x \to 0} {x^2 \over x}

Il punto di usare il limite è che la x dentro al limite non è esattamente uguale a 0, ma qualcosa di estremamente vicino, ancora più piccola di 0.0000000000001 ma diversa da 0, quindi possiamo dividere per essa.

Di conseguenza possiamo semplificare ed ottenere:

\displaystyle \lim_{x \to 0} {x^2 \over x} = \displaystyle \lim_{x \to 0} x = 0

Ovviamente il limite è uguale a 0 perché abbiamo supposto che, appunto, x tendesse a 0.

Vediamo un altro esempio molto interessante: prendiamo il limite per x che tende a 0 di f(x)={1\over x^2}. Come nel caso di prima, non possiamo sostituire 0 dentro la funzione perché non si può dividere per 0.

In questo caso però non abbiamo semplificazioni comode, dunque limitiamoci a sostituire valori di x sempre più vicini a 0 e vediamo come si comporta:

Se mettiamo 0.1 otteniamo 100, se mettiamo 0.0000001 ottenaimo 1'000'000'000'000. Notiamo che più piccoli sono i valori che inseriamo, più grande è il risultato. Quindi non c'è alcun numero intorno a cui si stabilizza.

Qualunque numero reale non va bene come limite, perché se mettiamo un valore abbastanza piccolo nella funzione lo supereremo. Dunque si dice che la funzione "tende a +\infty".

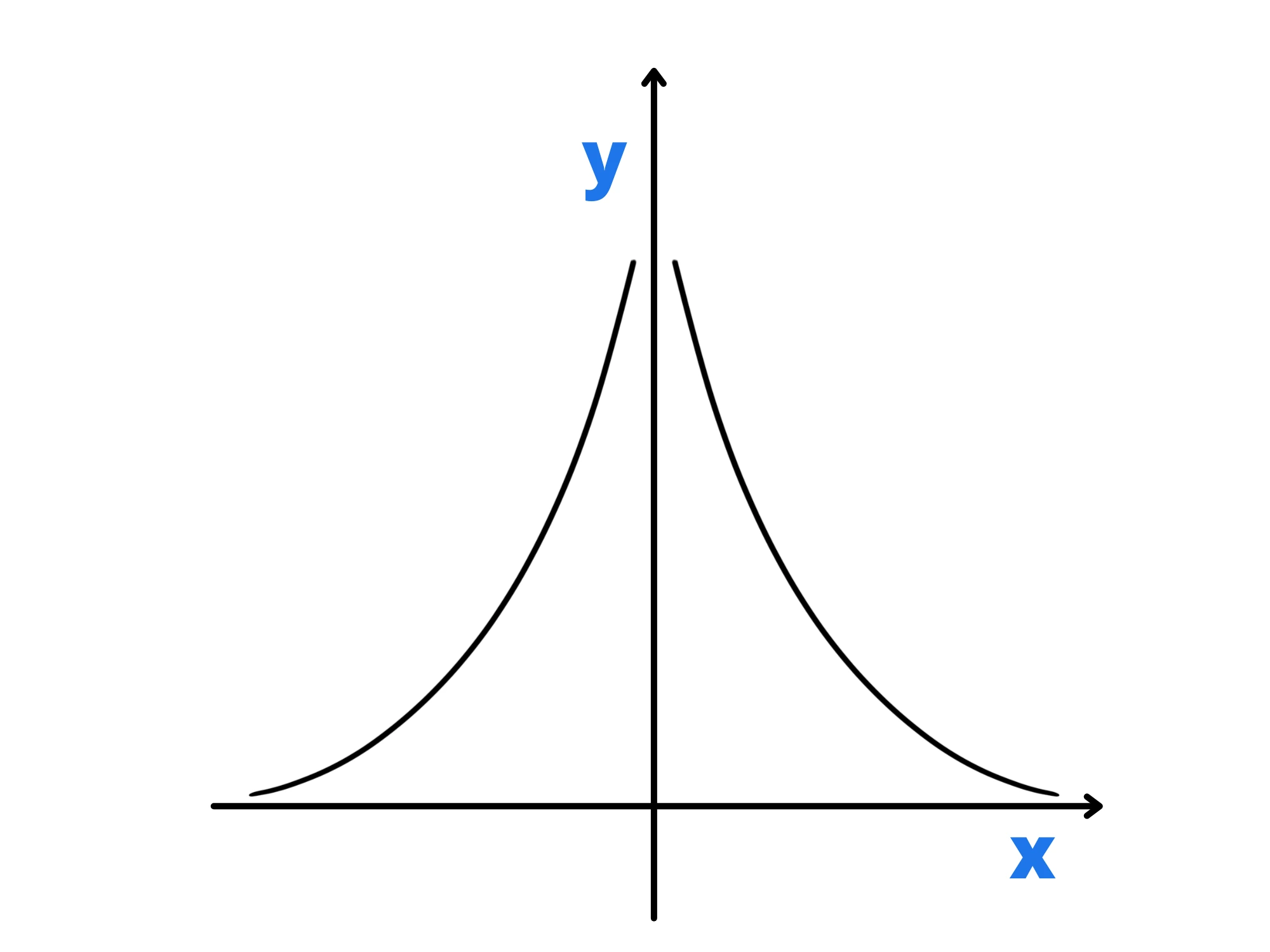
State attenti, sarebbe sbagliato dire che la funzione è uguale a +\infty. Infinito non è un numero, dire che tende a infinito vuol dire soltante che aumenta sempre di più, che non si stabilizza.

Notate che abbiamo scritto +\infty e non solo \infty perché bisogna differenziarlo da -\infty. Se infatti avessimo preso il limite di {-1 \over x^2}, avremmo ottenuto gli stessi numeri ma con un meno davanti. Nel primo caso quindi la funzione va "verso l'alto", mentre se ci sta il meno va "verso il basso" ed è dunque ovvio che sono due cose diverse.

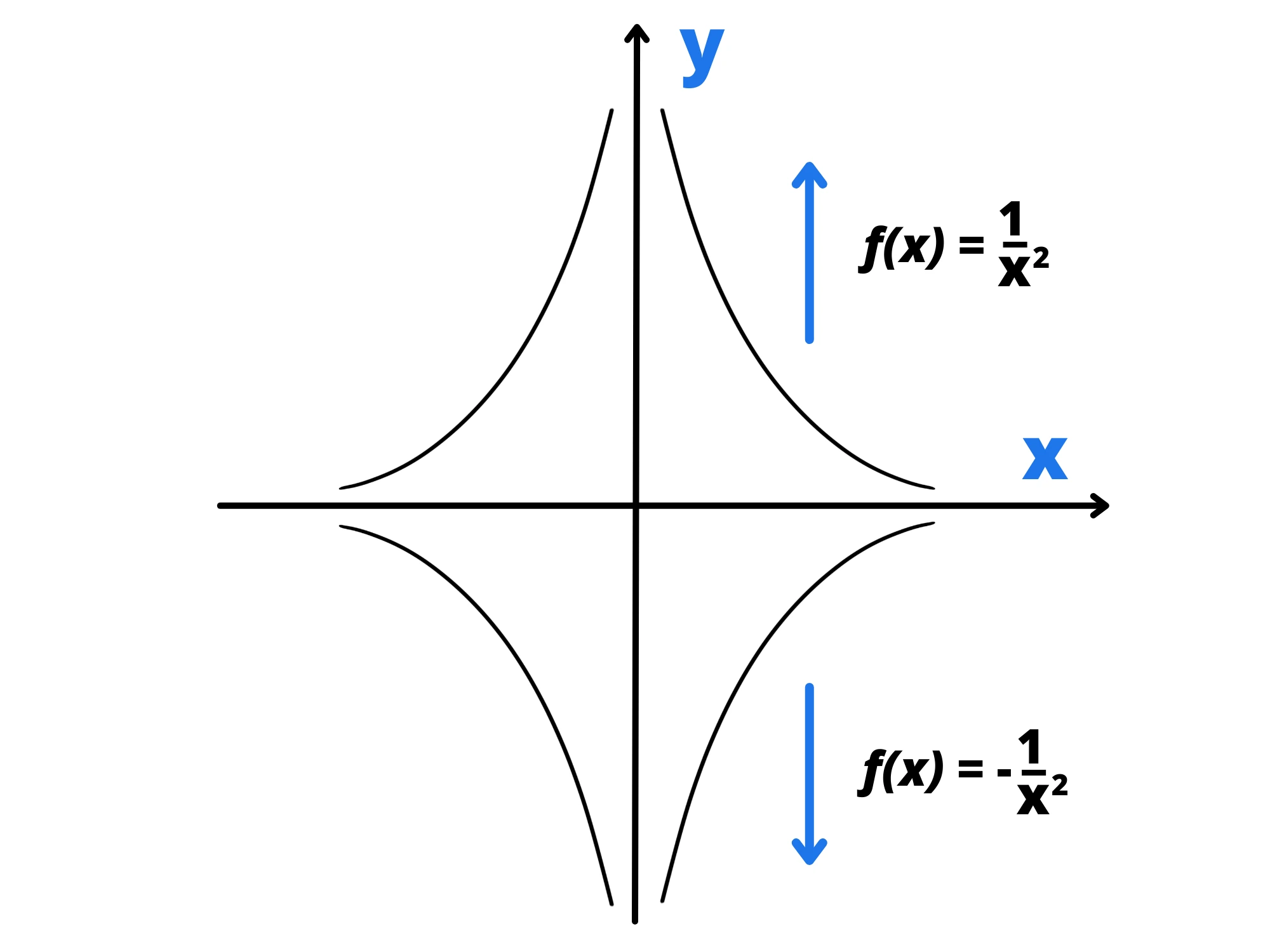
Vediamo un ultimo esempio interessante: prendiamo il limite per x che tende a 0 della funzione f(x)={1\over x}.

Se come prima mettiamo valori sempre più piccoli, notiamo che anche in questo caso aumenta sempre. Dunque anche questo limite è uguale a +\infty? No, perché c'è un'importantissima differenza.

Quando prendiamo il limite di una funzione, possiamo avvicinarci ad il valore della x da due "direzioni". Possiamo prendere un valore maggiore di x ed diminuirlo avvicinandoci sempre di più ad x, oppure possiamo prendere un valore minore di x ed aumentarlo, come vediamo nel grafico seguente:

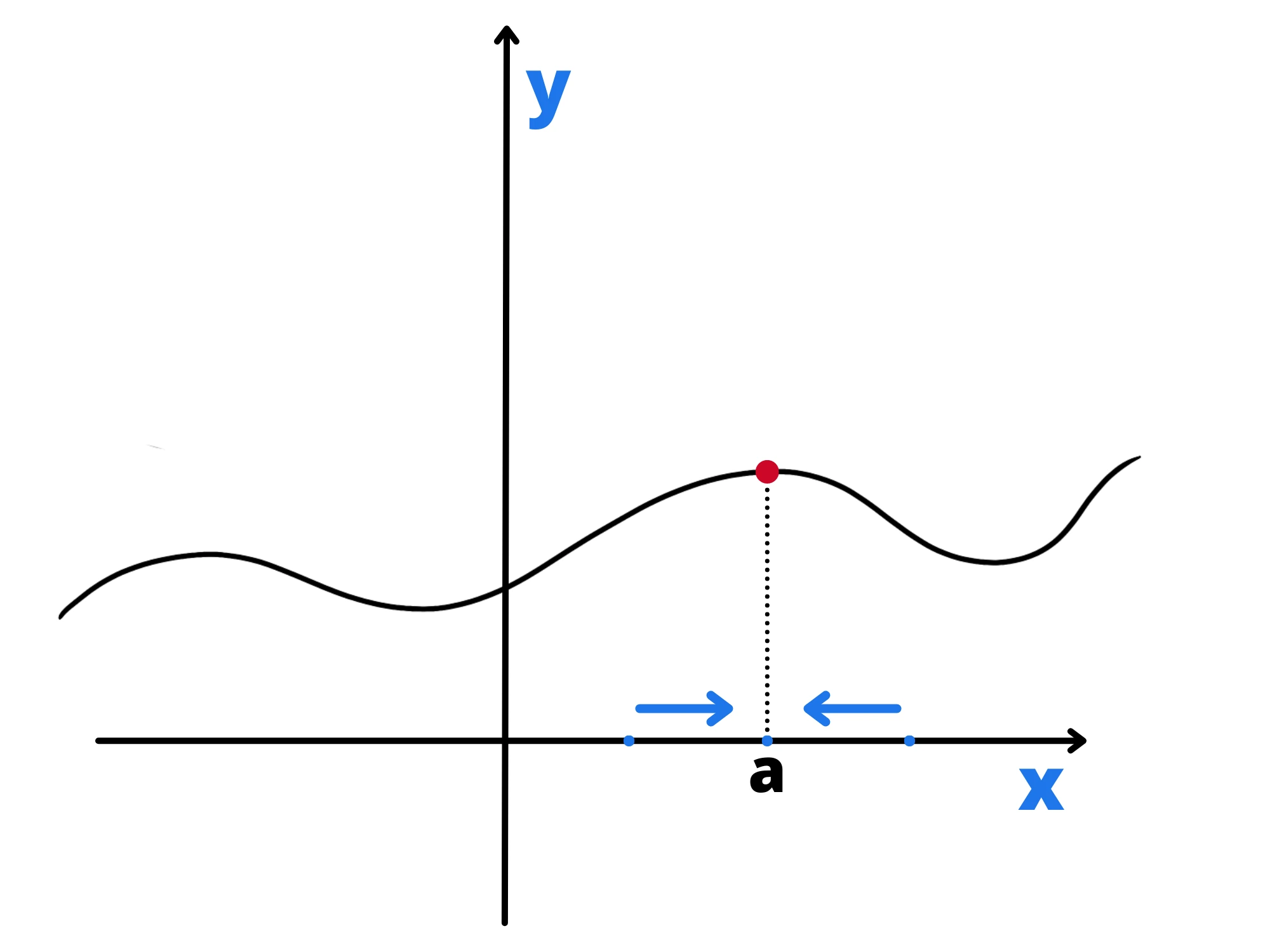
Possiamo quindi star arrivando da destra o da sinistra della x, per questo si chiamano "limite destro" e "limite sinistro". Negli esempi precedenti i due limiti erano uguali, potete dimostrarlo come esercizio, e dunque non c'era alcun problema.

Nell'ultimo esempio, però, se calcoliamo il limite destro otteniamo valori sempre più grandi ed è dunque uguale a +\infty. Se però calcoliamo il limite sinistro, prendiamo valori di x poco inferiori a 0 e quindi sono negativi.

Di conseguenza, {1\over x} darà valori negativi di valore assoluto sempre più grande, dunque il limite sinistro è uguale a -\infty. Quindi quanto vale il limite? Guardiamo il grafico della funzione:

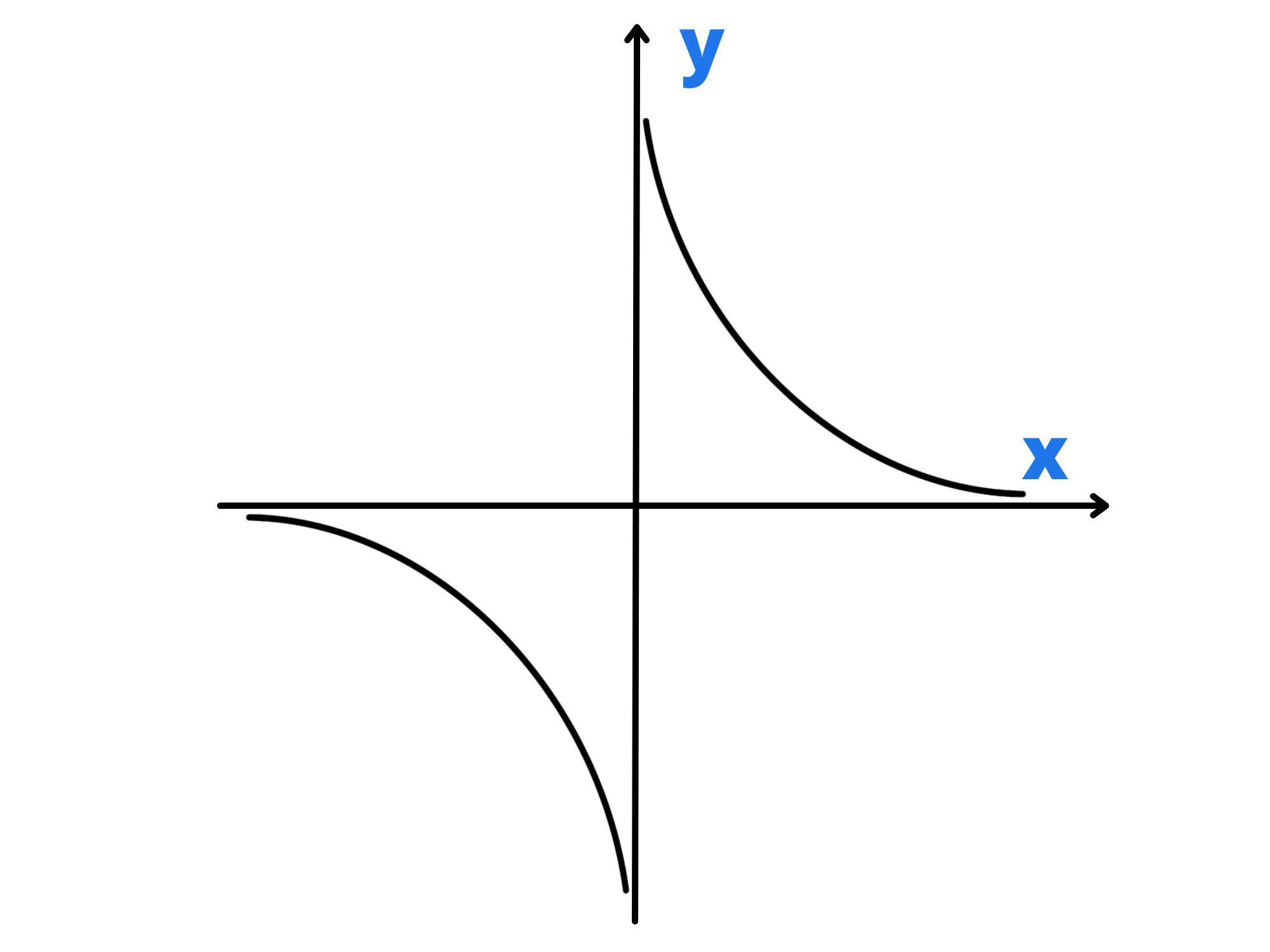
Notiamo che come abbiamo calcolato prima, se arriviamo da destra, andiamo sempre più in alto, mentre se arriviamo da sinistra andiamo sempre più in basso.

In questo caso il limite della funzione non esiste, perché non c'è alcun valor preciso a cui si avvicina sempre di più.

Quindi, il limite per x che tende ad un valore a di una funzione f(x) esiste se e solo se il suo limite di destra e il suo limite di sinistra sono uguali.

Se quindi abbiamo una funzione che presenta "un balzo" come la seguente:

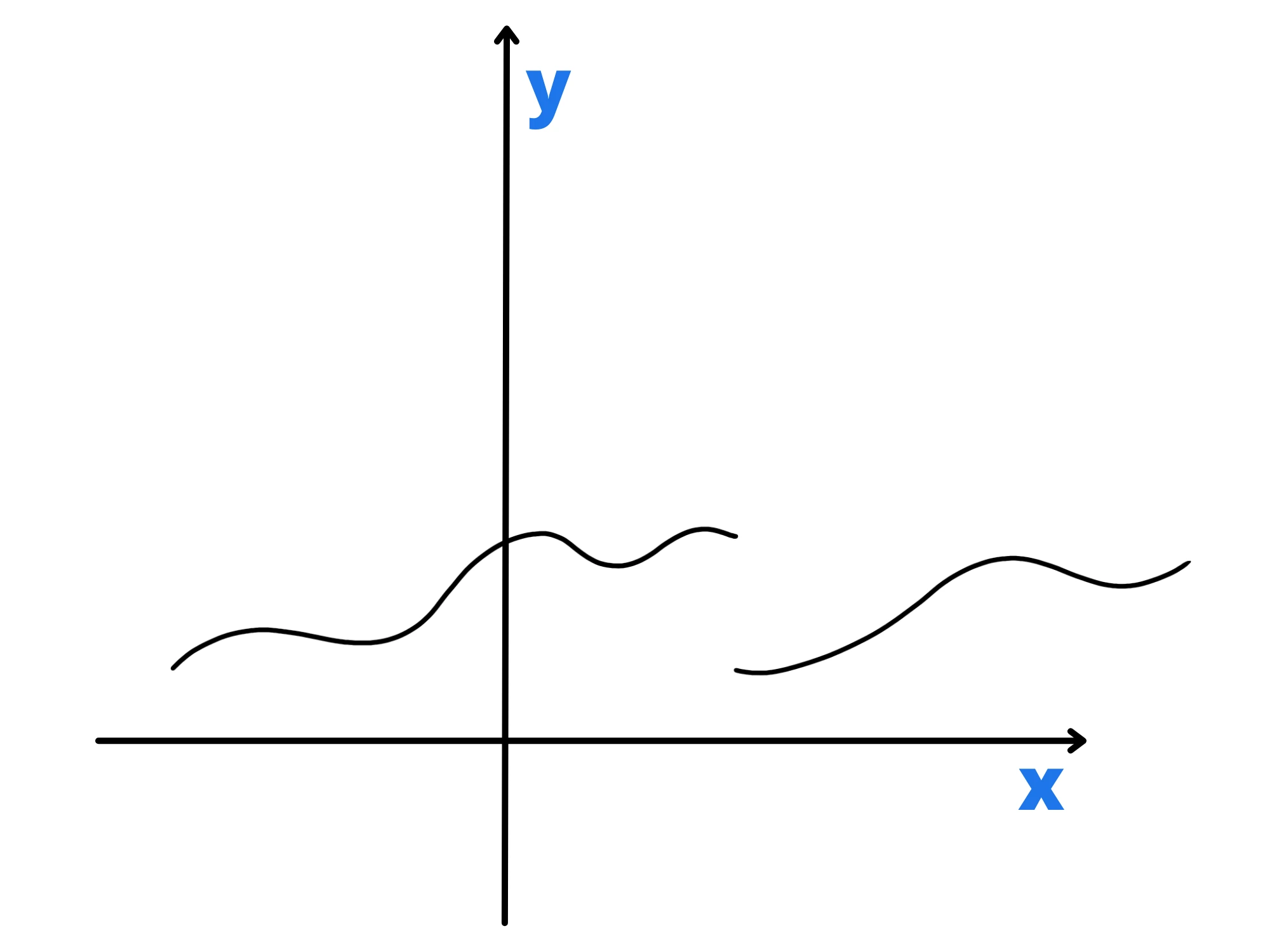
Il limite a quella discontinuità non esiste.

Proprietà dei limiti

Adesso che sappiamo cosa sia un limite, vediamo qualcuna delle loro proprietà:

Il limite della somma di due funzioni è uguale alla somma dei due limiti:

\displaystyle \lim_{x \to a} (f(x)+ g(x))= \displaystyle \lim_{x \to a} f(x) + \displaystyle \lim_{x \to a} g(x)

Stessa cosa vale per la differenza:

\displaystyle \lim_{x \to a} (f(x)- g(x))= \displaystyle \lim_{x \to a} f(x) - \displaystyle \lim_{x \to a} g(x)

Anche il limite di un prodotto di due funzioni è uguale al prodotto dei limiti:

\displaystyle \lim_{x \to a} (f(x)\cdot g(x))= \displaystyle \lim_{x \to a} f(x) \cdot \displaystyle \lim_{x \to a} g(x)

Perfino il limite di un quoziente (supponendo il denominatore diverso da 0) è uguale al quoziente dei limiti:

\displaystyle \lim_{x \to a} ({f(x) \over g(x)})= {\displaystyle \lim_{x \to a} f(x) \over \displaystyle \lim_{x \to a} g(x)}

Anche la composizione di due funzioni si comporta bene con i limiti:

\displaystyle \lim_{x \to a} f(g(x))= f(\displaystyle \lim_{x \to a} g(x))

Con questo concludiamo la lezione introduttiva sui limiti. Per altre informazioni potete guardare la lezione sui limiti notevoli (qui).