Flusso del campo elettrico

Cos'è il flusso del campo elettrico

Iniziamo prendendo un campo elettrico \overrightarrow{E}. Per semplicità, supponiamo che nella regione in cui lo stiamo osservando sia uniforme, cioè che i suoi vettori siano tutti uguali:

Ora prendiamo una superficie \Omega (Omega) di area S:

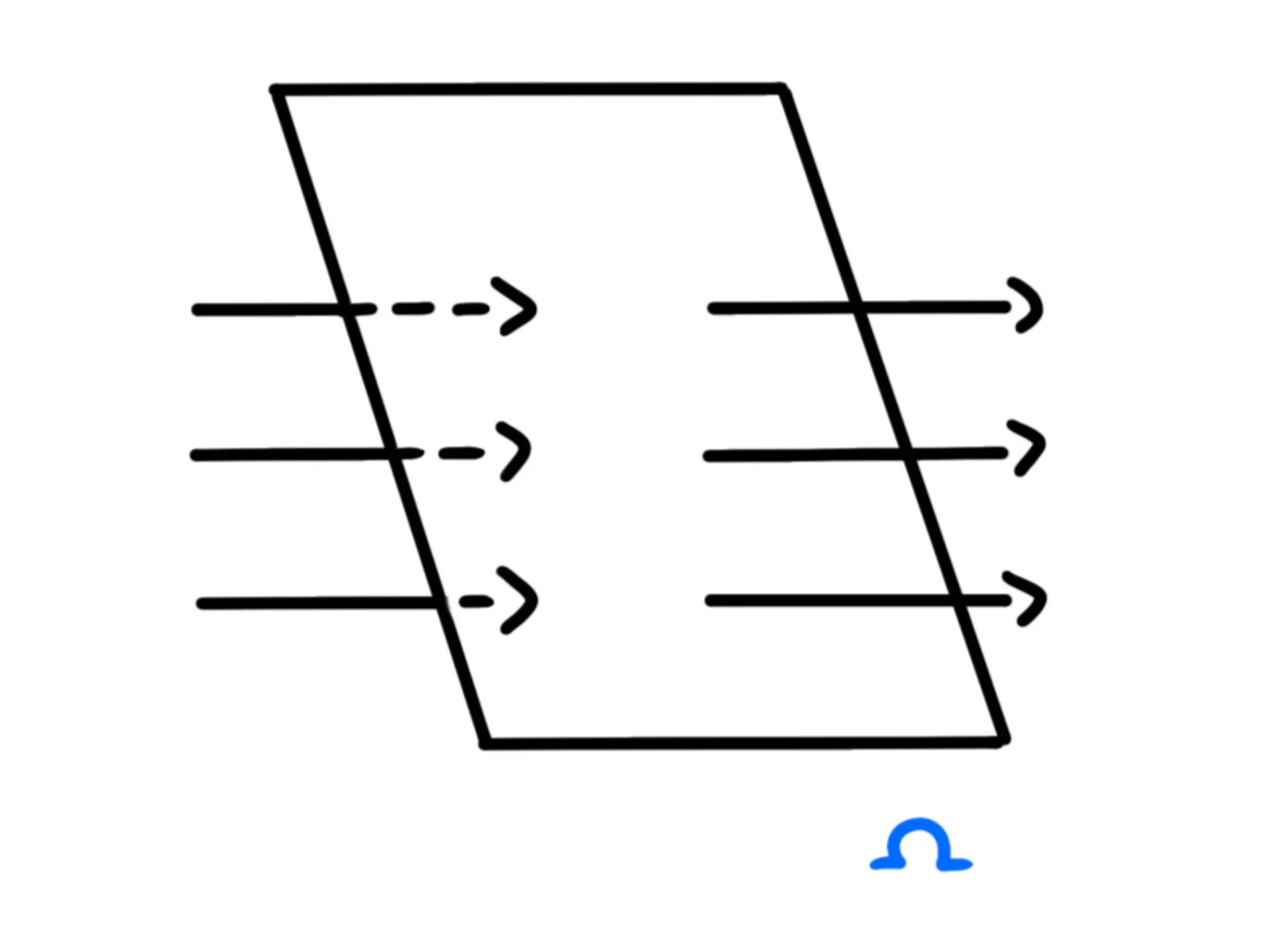
Infine prendiamo un vettore \overrightarrow{S} che abbia come modulo l'area S della superficie e direzione perpendicolare ad essa:

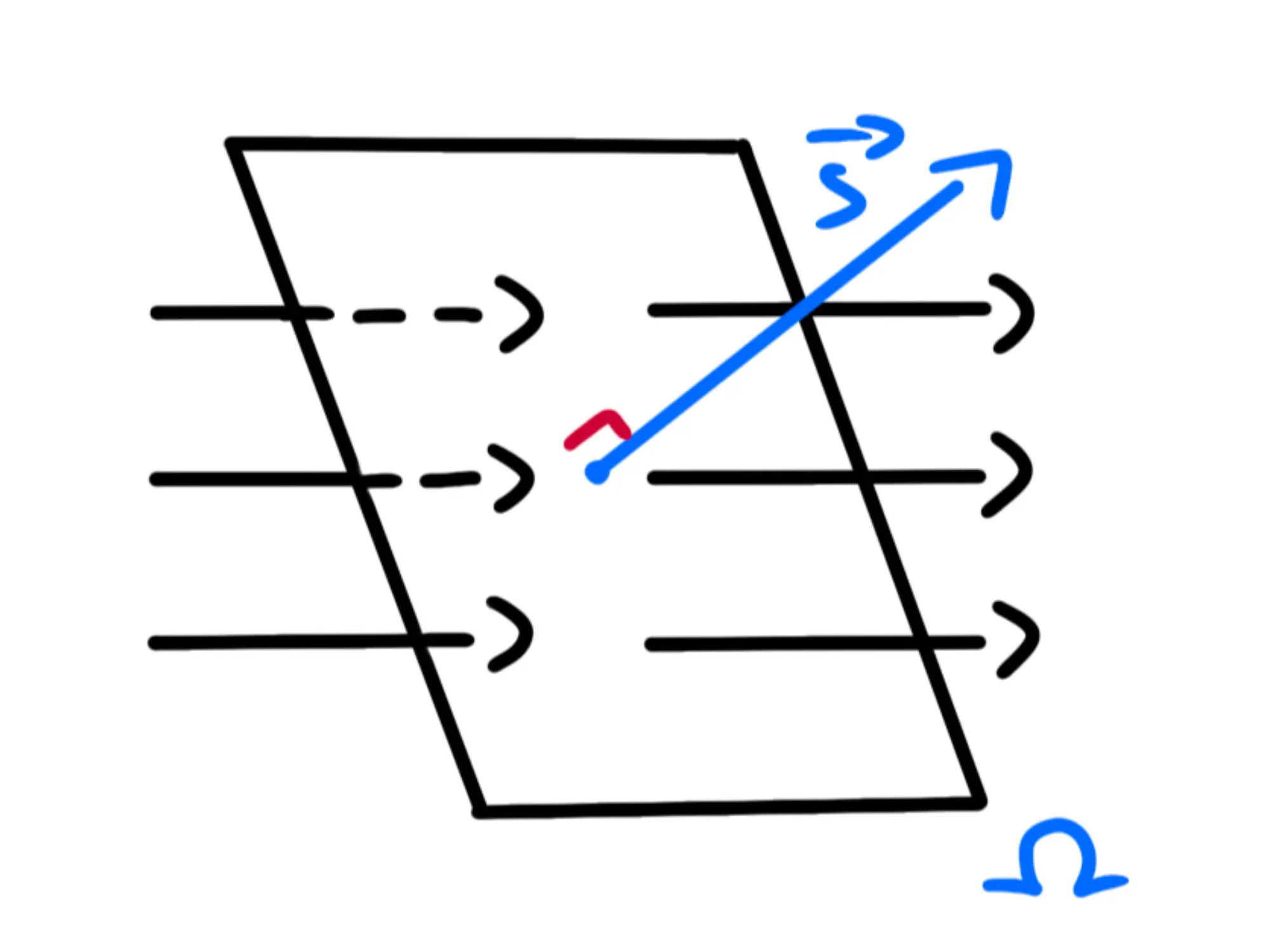
Qual'è il suo verso? Possiamo deciderlo noi, basta che scegliamo lo stesso verso per le varie supefici che abbiamo.

Ora siamo pronti a definire il flusso di \overrightarrow{E} che passa per \Omega:

In un campo elettrico uniforme \overrightarrow{E}, se la superficie \Omega è piana, allora il flusso \Phi_{\Omega}(\overrightarrow{E}) è il prodotto scalare tra un vettore di \overrightarrow{E} e il vettore superificie \overrightarrow{S} di \Omega:

\Phi_{\Omega}(\overrightarrow{E}) = \overrightarrow{E} \cdot \overrightarrow{S}

Se dunque chiamiamo \theta l'angolo tra la superficie e il campo elettrico, otteniamo:

\Phi_{\Omega}(\overrightarrow{E}) = ES\cos(\theta)

Dunque la sua unità di misura è il Newton per metro quadro su Coulomb ({Nm^2\over C}).

Ok, ora abbiamo visto come si calcola, ma come mi rappresenta effettivamente? Dobbiamo immaginare che i vettori del campo elettrico siano come palline che si muovono nella direzione della loro freccia. Quello che ci dice il flusso del campo elettrico è quante palline passano per quella superficie.

Questo ci dice anche, quindi, che il flusso del campo elettrico \overrightarrow{E} su una superficie \Omega è proporzionale al numero delle linee di campo che tagliano \Omega.

Ora può sembrare una cosa un po' inutile, ma in questa lezione, più avanti, vedremo come ci aiuterà a risolvere alcuni problemi.

Prima, però, dobbiamo generalizzare come si calcola questo flusso, perché per ora abbiamo solo visto un caso molto particolare.

Guardiamo che succede se la superficie è curva ma il campo elettrico rimane uniforme. Avremo qualcosa di questo tipo:

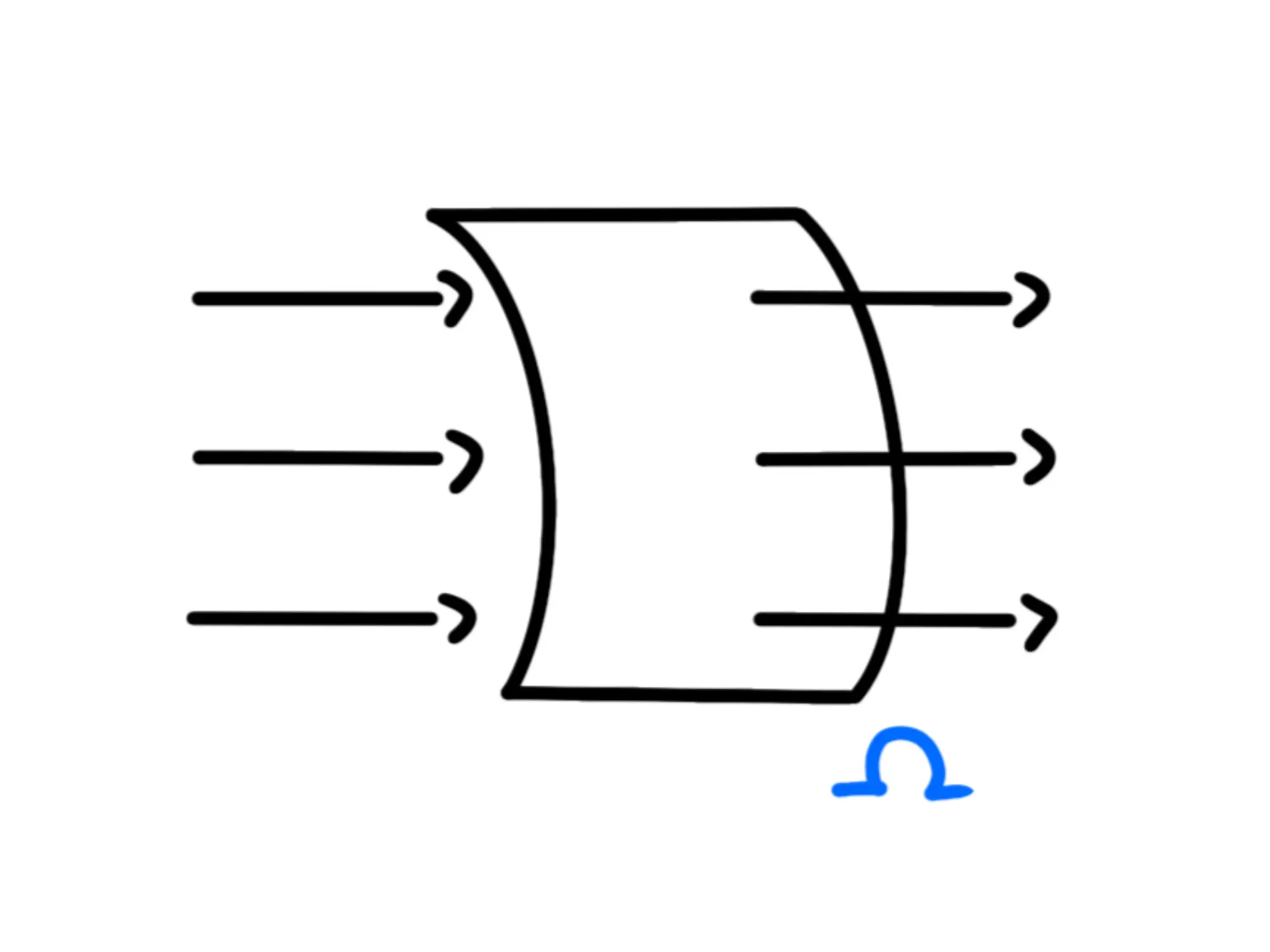
Adesso non esiste più un unico vettore \overrightarrow{S} perpendicolare a tutta la superficie, quindi come fare?

Per risolvere il problema, immaginiamo di dividere la nostra superifice in tanti piccoli rettangolini:

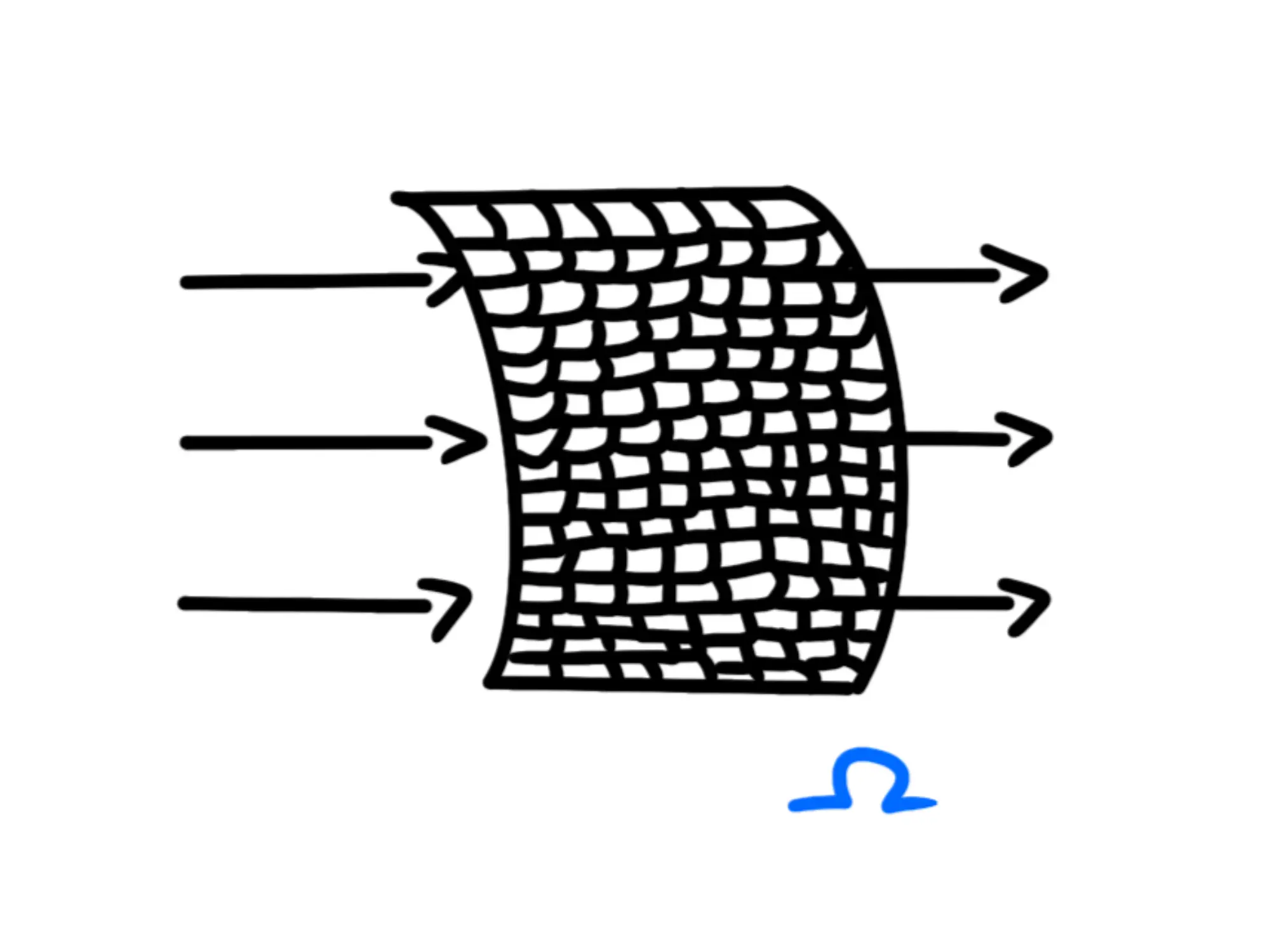
Se il numero di rettangoli è abbastanza grande, essi approssimeranno molto bene la nostra superficie. Perché abbiamo fatto questo? Perché ogni rettangolino è una superficie piana, quindi possiamo calcolare il flusso per ognuno di essi e sommarli insieme. L'i-esimo rettangolino avrà un vettore superficie \Delta \overrightarrow{S_i} perpendicolare ad esso e con modulo l'area del rettangolino.

Quindi il flusso del campo elettrico passante per l'i-esimo rettangolino sarà uguale a \overrightarrow{E} \cdot \Delta \overrightarrow{ S_i}.

Se abbiamo N rettangolini, avremo che il flusso totale sarà uguale a:

\Phi_{\Omega}(\overrightarrow{E}) = \sum_{i=1}^N \overrightarrow{E}\cdot \Delta\overrightarrow{ S_i}

Se vi state chiedendo perché abbiamo chiamato così il piccolo vettore \Delta \overrightarrow{S_i} e non semplicemente \overrightarrow{S_i}, è perché ci aiuta a capire meglio che si tratta del vettore superifice di soltanto un pezzettino di \Omega e perché se poi vogliamo usare gli integrali per calcolare il flusso, questa notazione rende le cose più chiare.

Infatti, se dividessimo \Omega in un numero infiniti di pezzettini, l'approssimazione diventerebbe una vera e propria uguaglianza, ma siccome gli integrali di superficie non vengono studiati al liceo, non ne parleremo in questa lezione.

Quindi, se non possiamo ancora usare gli integrali, quanto deve essere il numero N di rettanngoli in cui divido \Omega affinchè il risultato sia un'approssimazione accettabile? Dipende, non esiste una regola per deciderlo, ma tanto non vi chiederanno mai di mettervi a calcolare i singoli prodotti scalari per poi sommarli insieme, in tutti i problemi che vi proporranno ci sarà sempre una qualche scorciatoia.

Ora non ci rimane che guardare al caso in cui la superficie \Omega può essere curva e il campo elettrico non è uniforme. Una volta capito il caso precedente, questo è un gioco da ragazzi. Perché se abbiamo diviso \Omega in tanti rettangolini piccolissimi, se sono così piccoli, il campo elettrico sarà circa uniforme vicino a quel rettangolo.

Quindi il campo elettrico varierà da rettangolo a rettangolo, ma dentro ad ognuno di essi sarà circa uniforme. Quindi nell'i-esimo rettangolo passerà un campo elettrico uniforme \overrightarrow{E_i} e se il suo vettore superficie è \Delta \overrightarrow{S_i}, allora il flusso passante per il rettangolino sarà \overrightarrow{E_i} \cdot \Delta \overrightarrow{S_i}.

Quindi, se abbiamo N rettangoli, ci basterà sommare il flusso di ognuno di essi per ottenere quello di \Omega:

\Phi_{\Omega}(\overrightarrow{E}) = \sum_{i=1}^N \overrightarrow{E_i}\cdot \Delta\overrightarrow{ S_i}

Anche in questo caso qua, non dovrete mai veramente mettervi a sommare il flusso di tutti i rettangolini, ma userete varie scorciatoie.

Ma quali sono questi trucchetti che ti permettono di calcolare il flusso molto più velocemente? Vediamo subito il più importante e utile di essi: il Teorema di Gauss.

Teorema di Gauss

Il teorema di Gauss ci dice che il flusso di un campo elettrico per una superficie chiusa \Omega è uguale alla quantità di carica totale Q contenuta dentro \Omega divisa per la costante dielettrica del vuoto \epsilon_0:

\Phi_{\Omega}(\overrightarrow{E}) = {Q\over \epsilon_0}

Questo ovviamente è vero nel vuoto, se siamo in un qualsiasi altro mezzo dobbiamo mettere la costante dielettrica assoluta del mezzo \epsilon al posto di \epsilon_0 :

\Phi_{\Omega}(\overrightarrow{E}) = {Q\over \epsilon}

Mi raccomando, ricordatevi che questo è vero solo per superfici chiuse. Per chi si fosse dimenticato cosa sia una superficie chiusa, essa è la superficie senza buchi di un solido.

Come possiamo dimostrarlo? Partiamo dal caso più semplice, quello in cui la superficie sia una sfera e in cui tutta la carica Q si trovi al centro della sfera e sia positiva:

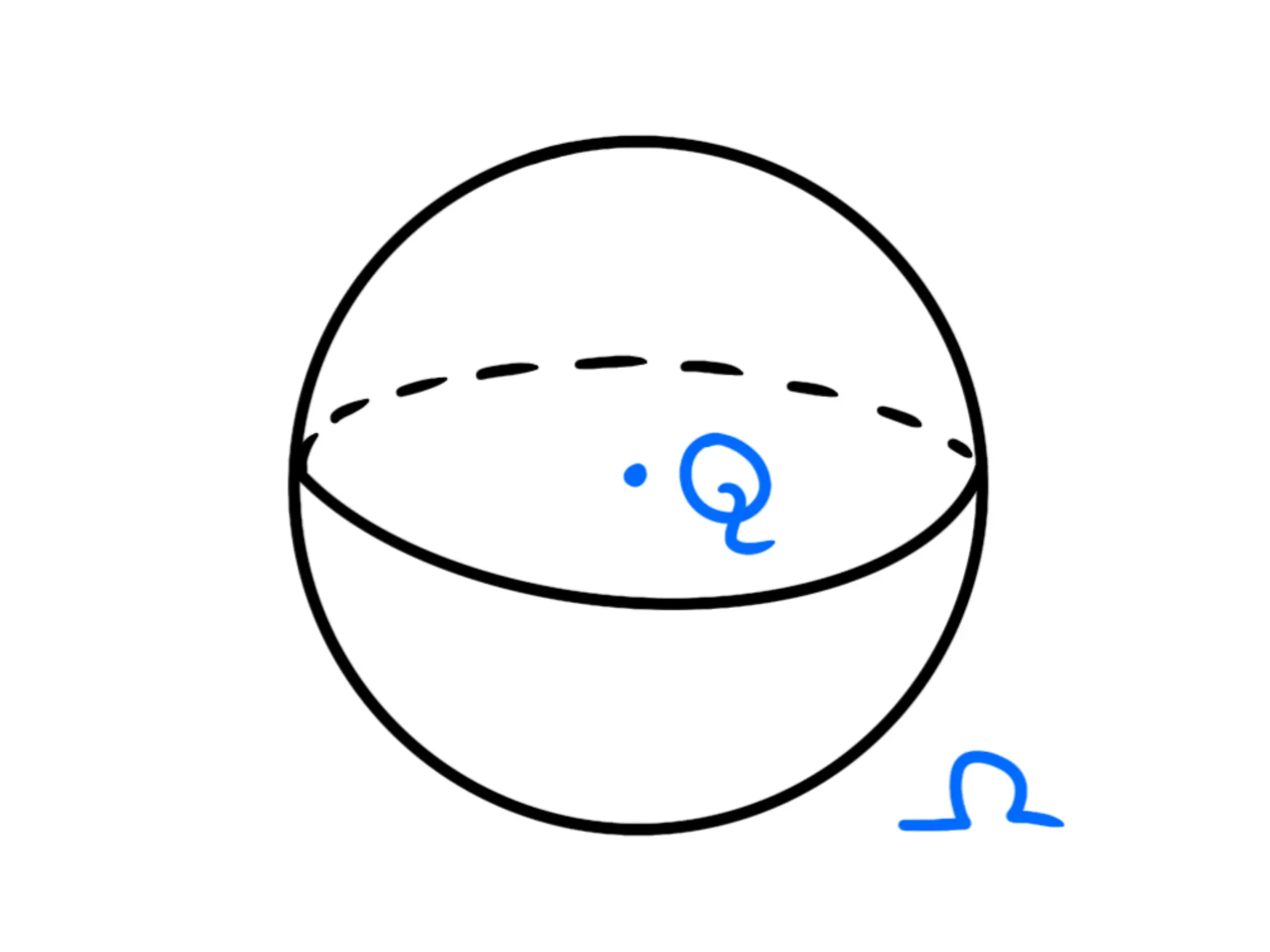
Si tratta del caso più generale di cui avevamo parlato nello scorso capitolo: il campo non è uniforme e la superficie non è piana. Dividiamo quindi la sfera in tanti piccoli rettangolini e vediamo cosa succede (per semplicità ora vediamo cosa succede ad un solo rettangolino, tanto poi gli altri si comportano nello stesso modo):

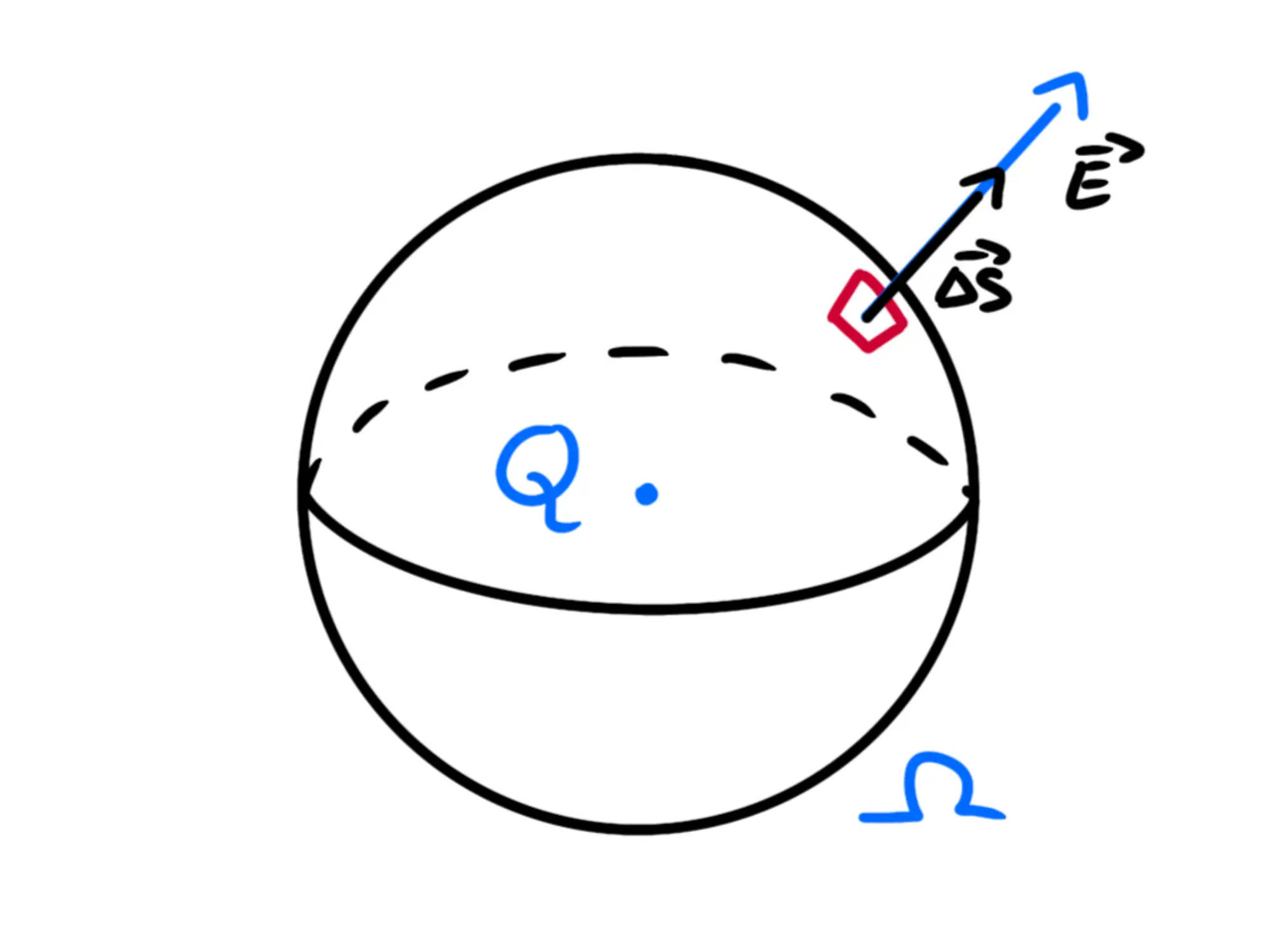
Notiamo quindi che \overrightarrow{E} e \Delta \overrightarrow{S} sono paralleli e dunque il loro prodotto scalare è uguale al prodotto dei loro moduli:

\overrightarrow{E} \cdot \Delta \overrightarrow{S} = E \Delta S

Ci ricordiamo poi la formula per calcolare il campo elettrico generato da una carica Q puntiforme:

E = {1\over 4 \pi \epsilon_0} {|Q|\over r^2}

Siccome Q è positiva abbiamo:

E = {1\over 4\pi\epsilon_0} {Q\over r^2}

Notiamo quindi che il modulo del campo elettrico dipende soltanto dalla carica che lo induce e dalla distanza da essa. Ma per definizione, la sfera è il luogo geometrico dei punti equidistanti dal suo centro, dunque sulla superficie della sfera r è costante. Dunque, siccome la carica non varia, il modulo del campo elettrico deve essere costante su \Omega.

Detto questo siamo pronti a calcolare il flusso del campo elettrico su \Omega. Usando la formula generale che avevamo trovato prima abbiamo:

\Phi_{\Omega}(\overrightarrow{E}) = \sum_{i=1}^N \overrightarrow{E_i} \cdot \Delta \overrightarrow{S_i}

Ma avevamo detto prima che il campo elettrico è parallelo al vettore superficie e che dunque \overrightarrow{E_i} \cdot \Delta \overrightarrow{S_i} è uguale a E_i \Delta S_i. Sostituendo abbiamo:

\Phi_{\Omega}(\overrightarrow{E}) = \sum_{i=1}^N E_i \cdot \Delta S_i

Poi avevamo detto che E è costante su tutta la sfera, dunque tutti gli E_i sono uguali a E e posso dunque sostituirlo:

\Phi_{\Omega}(\overrightarrow{E}) = \sum_{i=1}^N E \cdot \Delta S_i

Ma ora E è una costante nella sommatoria, dunque posso portarlo fuori di essa:

\Phi_{\Omega}(\overrightarrow{E}) = E \cdot \sum_{i=1}^N \Delta S_i

E la somma delle aree di tutti i rettangoli è uguale all'area della sfera, quindi:

\Phi_{\Omega}(\overrightarrow{E}) = E \cdot S

Ma l'area della sfera è uguale a 4\pi r^2 e sostituendo pure {1\over 4 \pi \epsilon_0} {Q\over \epsilon_0} al posto di E otteniamo:

\Phi_{\Omega}(\overrightarrow{E}) = {1\over 4 \pi \epsilon_0} {Q\over r^2} \cdot 4 \pi r^2

\Phi_{\Omega}(\overrightarrow{E}) = {Q \over \epsilon_0}

Ed ecco dimostrato il teorema di Gauss nel nostro caso particolare. Ora, se al posto di una carica positiva ne avevamo una negativa, allora il verso del campo elettrico cambiava, dunque avremmo avuto \overrightarrow{E} \cdot \Delta \overrightarrow{S} = - E \Delta S. Però nella formula per il campo elettrico, avremmo avuto che, essendo Q negativa, il suo modulo era uguale a -Q. Dunque sarebbe comparso un altro segno meno che si sarebbe semplificato con quell'altro ed avremmo ottenuto lo stesso risultato.

E se abbiamo una qualsiasi superficie chiusa e non una sfera? E se la carica non si trova tutta al centro ma sparpagliata dentro la superficie?

Per risolvere questi altri casi, ci basta ricordare che il flusso del campo elettrico è proporzionale al numero di linee di campo che passano per quella superficie. Dunque la posizione della carica non importa perché il numero delle linee di campo sarà lo stesso:

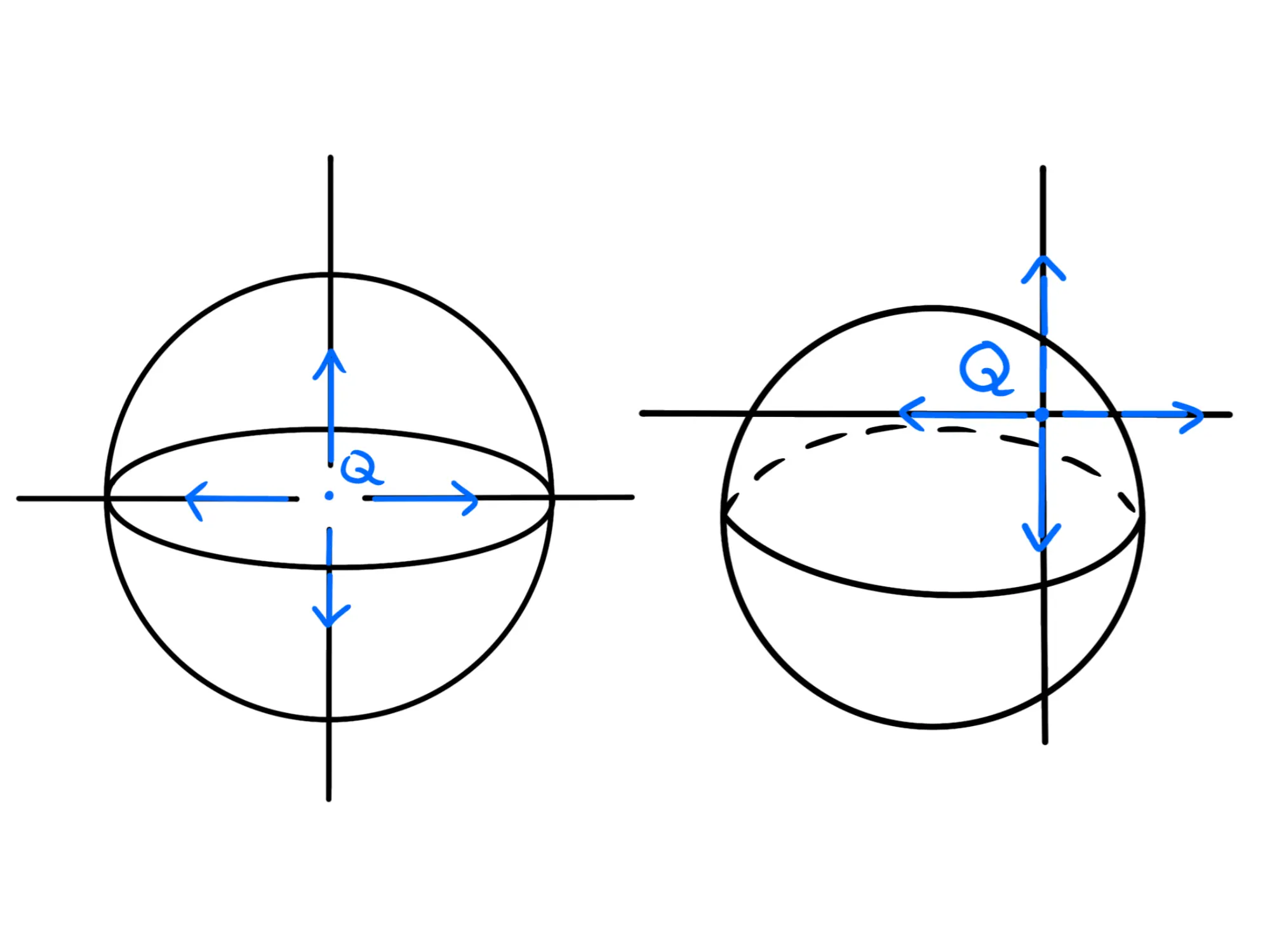
E se modichiamo la sfera senza bucarla, possiamo ottenere qualsiasi altra superficie chiusa e per di essa passeranno lo stesso numero di linee di campo:

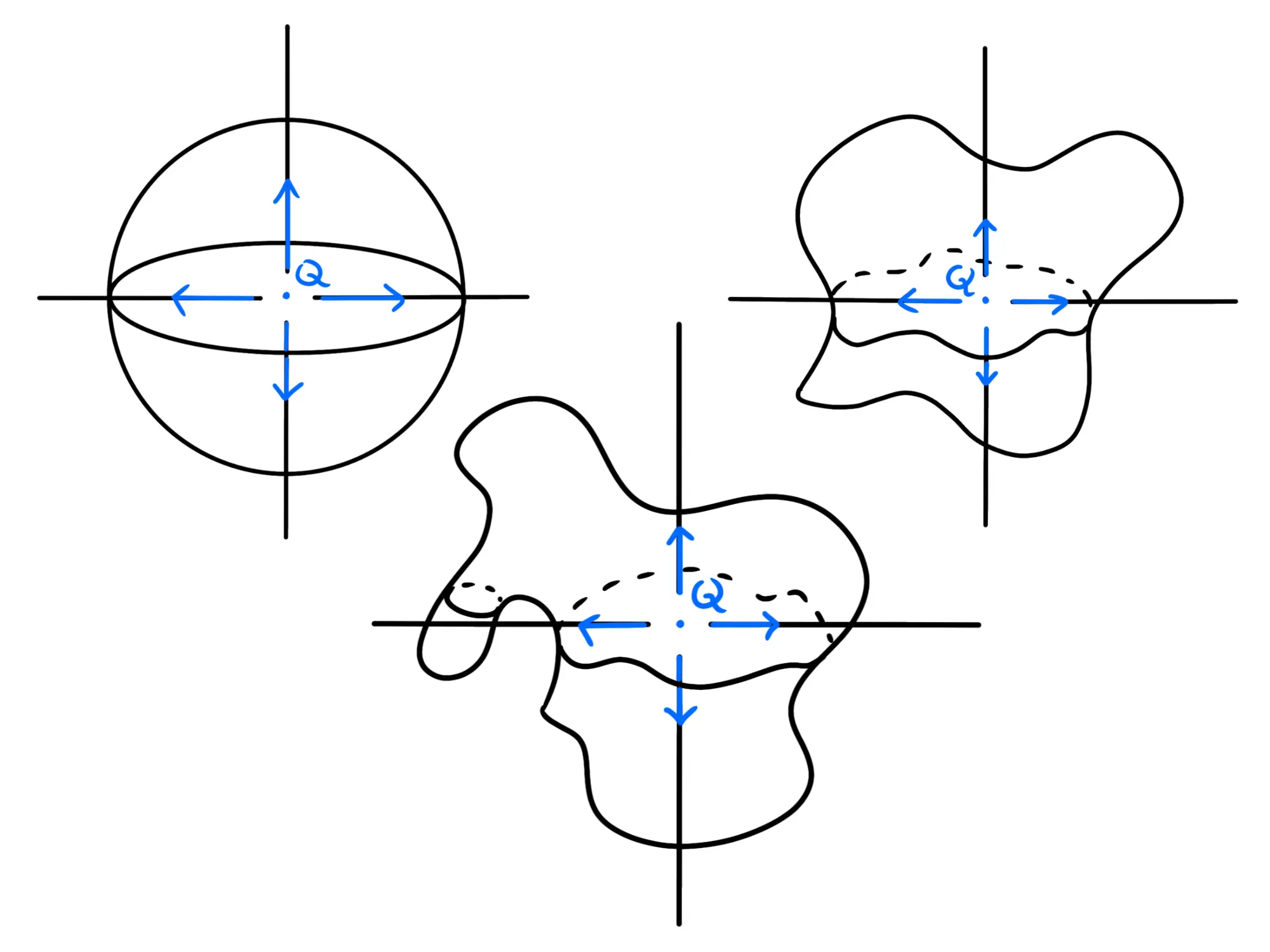
Notate che nella terza superficie, anche se una delle linee di campo esce due volte dalla superficie, siccome essa è chiusa, deve anche rientrare una volta, quindi la volta in più in cui esce e la volta in cui rientra si annullano a vicenda e le linee di campo che effettivamente passano per la superficie rimangono sempre 4.