Cariche elettriche

Corpi elettrizzati

Se prendete una penna e la strofinate con un panno di lana, noterete che comincerà ad attrarre piccoli pezzetti di carta.

Gli antichi non avevano le penne di plastica, ed usavano dunque l'ambra, che in greco antico si dice "elektron", per questo chiamiamo un corpo con questa caratteristica un corpo elettrizzato.

Questo metodo per elettrizzare i corpi strofinandoli viene chiamato elettrizzazione per strofinìo.

Se facciamo più esperimenti, notiamo che se prendiamo due corpi elettrizzati, essi si possono respingere o attrarre:

Se elettriziamo due bacchette di plastica, esse si respingeranno. Anche se sono due bacchette di vetro si respingeranno. Se però ne prendiamo una di plastica ed una di vetro, si attrarranno.

I simili si respingono mentre quelli diversi si attraggono.

Per formalizzare meglio questo concetto, dobbiamo introdurre la nozione di carica elettrica:

Facendo esperimenti, si scopre che tutti i corpi elettrizzati o si comportano come il vetro, oppure come la plastica.

Per questo, conferiamo ad ogni corpo elettrizato una carica e il segno di quest'ultima derivererà dal comportamento del corpo:

Un corpo elettrizzato ha una carica elettrica positiva se si comporta come il vetro, mentre ha una carica elettrice negativa se si comporta come la plastica.

Non c'è una ragione specifica per cui il vetro ha carica positiva e la plastica negativa, poteva anche essere il contrario, ma abbiamo scelto questa classificazione per convenzione.

Ora, possiamo formalizzare il concetto di prima:

Corpi elettrizzati con cariche elettriche dello stesso segno si respingono, metre quelli con cariche elettriche di segno opposto si attraggono.

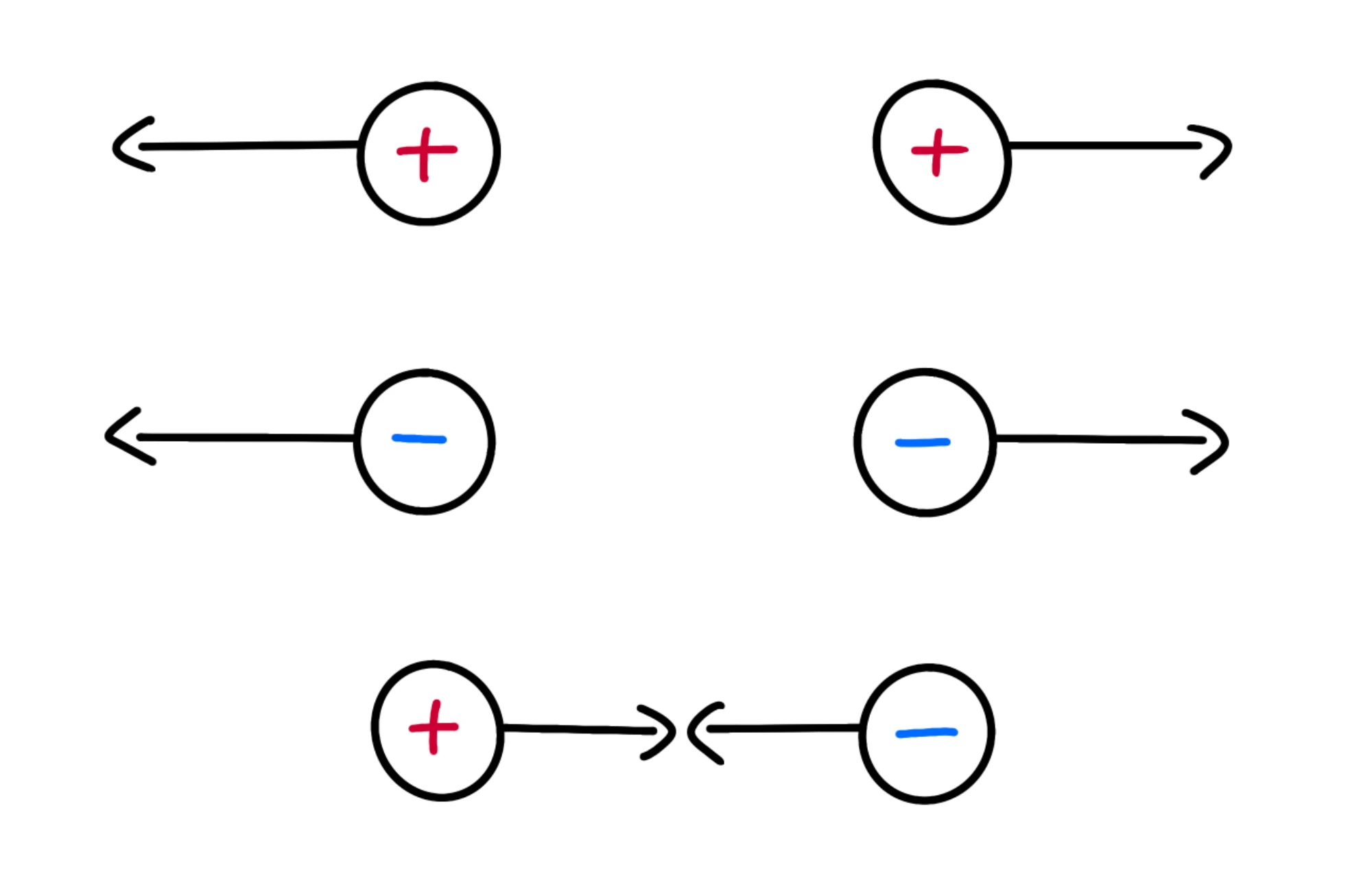
Adesso vediamo perché i corpi acquistano delle cariche:

L'atomo

Sappiamo bene che l'atomo è formato da elettroni e da un nucleo, a sua volta formato da neutroni e protoni. I protoni e gli elettroni hanno cariche elettriche, mentre il neutrone è neutro.

Per convenzione, si è deciso di dare la carica positiva al protone e quella negativa all'elettrone.

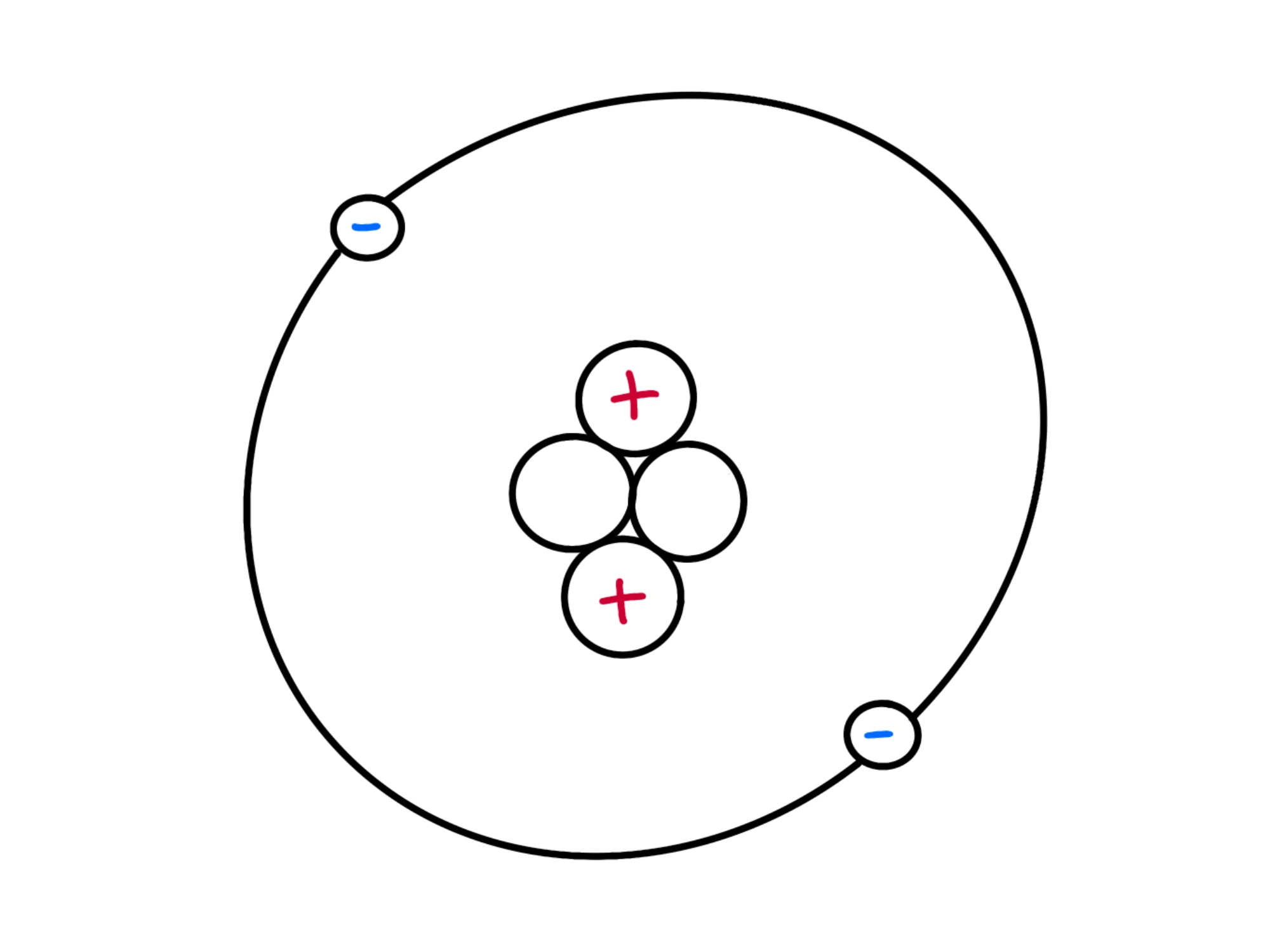
Facendo gli esperimenti, si scopre che la carica del protone è esattamente uguale a quella dell'elettrone (ma con segno opposto) ed essa viene chiamata e e vale circa:

e \approx 1,6022 \cdot 10^{-19} C

C è il Coulomb, l'unità di misura delle cariche elettriche, chiamata così in onore del fisico Charles Augustin Coulomb.

Se in un atomo il numero di elettroni è uguale a quello dei protoni, esso sarà neutro. Se però togliamo degli elettroni, si caricherà positivamente, perché avrà più protoni che elettroni.

Per questo, il vetro si carica positivamente perché quando viene strofinato cede degli elettroni.

Siccome un atomo può avere solo un numero intero di elettroni e protoni, non può avere mezzo elettrone, tutte le cariche elettriche sono multipli della carica dell'elettrone e.

Ricordatevi che sono solo gli elettroni a muoversi, non i protoni. Se un corpo si carica negativamente, vuol dire che ha acquistato degli elettroni, mentre se si carica positivamente ha ceduto degli elettroni. Il numero dei protoni non cambia.

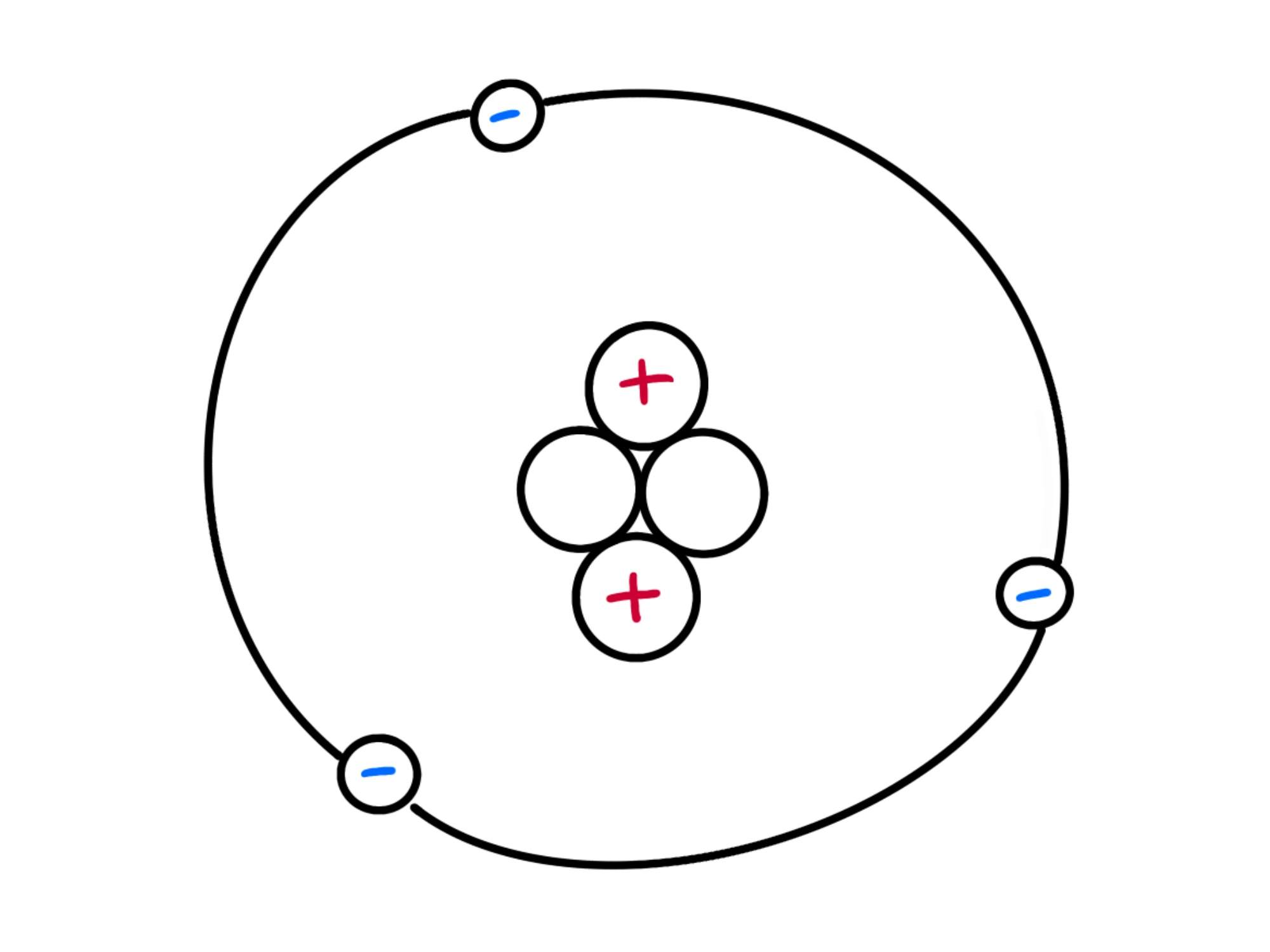
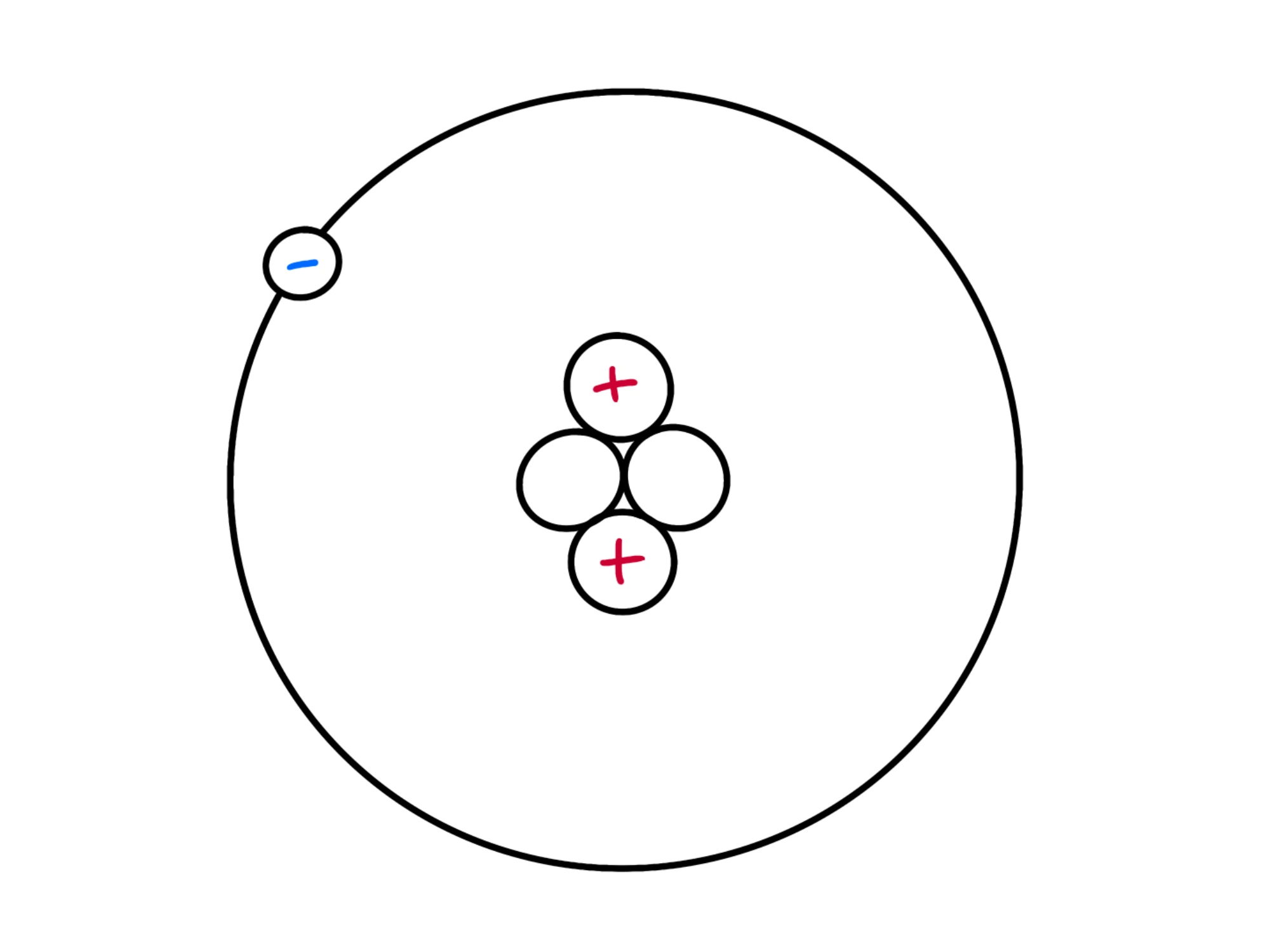
Isolanti e conduttori

Se proviamo a fare lo stesso esperimento ma al posto di usare delle bacchette di vetro e di plastica usiamo un cucchiaio di ferro, notiamo che non succede niente.

Il cucchiaio non riesce dunque ad elettrizzarsi? No, si elettrizza, ma il problema è che esso è un conduttore.

Gli elettroni del ferro, essendo quest'ultimo un metallo, sono molto liberi di muoversi. Anche il vostro corpo è un ottimo conduttore. Per questo, quando il ferro acquisisce degli elettroni, essi sono liberi di passare nel tuo corpo e poi per terra.

Il vetro e la plastica, invece, sono isolanti, perché i loro elettroni sono più legati ai loro nuclei, perciò li cedono molto più difficilemente al tuo corpo e dunque se li tengono.

Per risolvere il problema, basterà indossare un guanto isolante. In questo modo il cucchiaio non potrà passare al tuo corpo gli elettroni e rimarrà carico negativamente.

Altri metodi per elettrizzare un corpo

Oltre che per strofinìo, possiamo elettrizzare un corpo anche per contatto o per induzione.

Se prendimo un conduttore carico negativamente e un conduttore neutro, se li mettiamo in contatto, parte degli elettroni in eccesso del primo saranno liberi di andare nel secondo, caricandolo così negativamente. I due conduttori devono essere in contatto solo con altri isoltanti o le cariche potrebbero essere disperse:

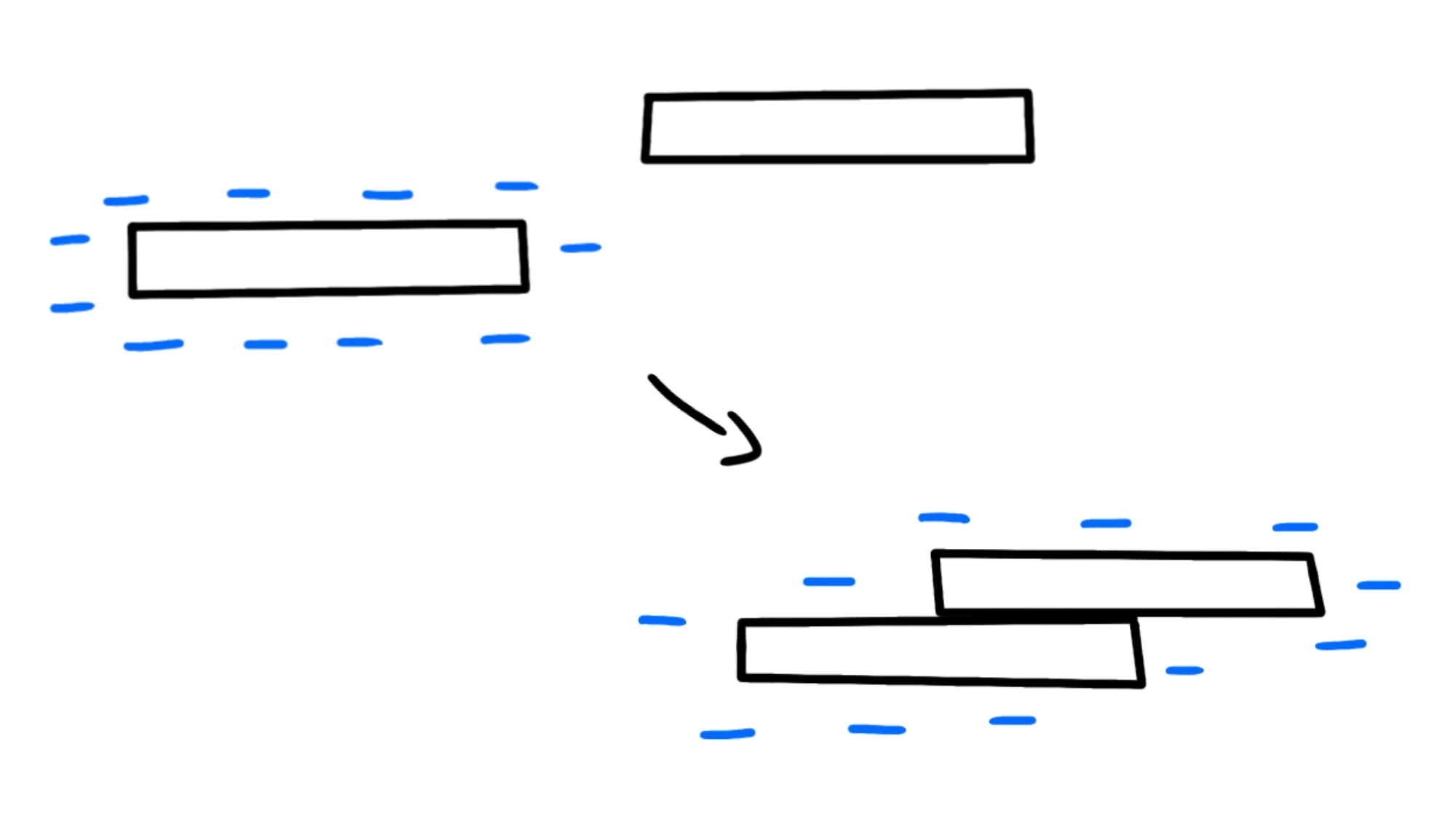
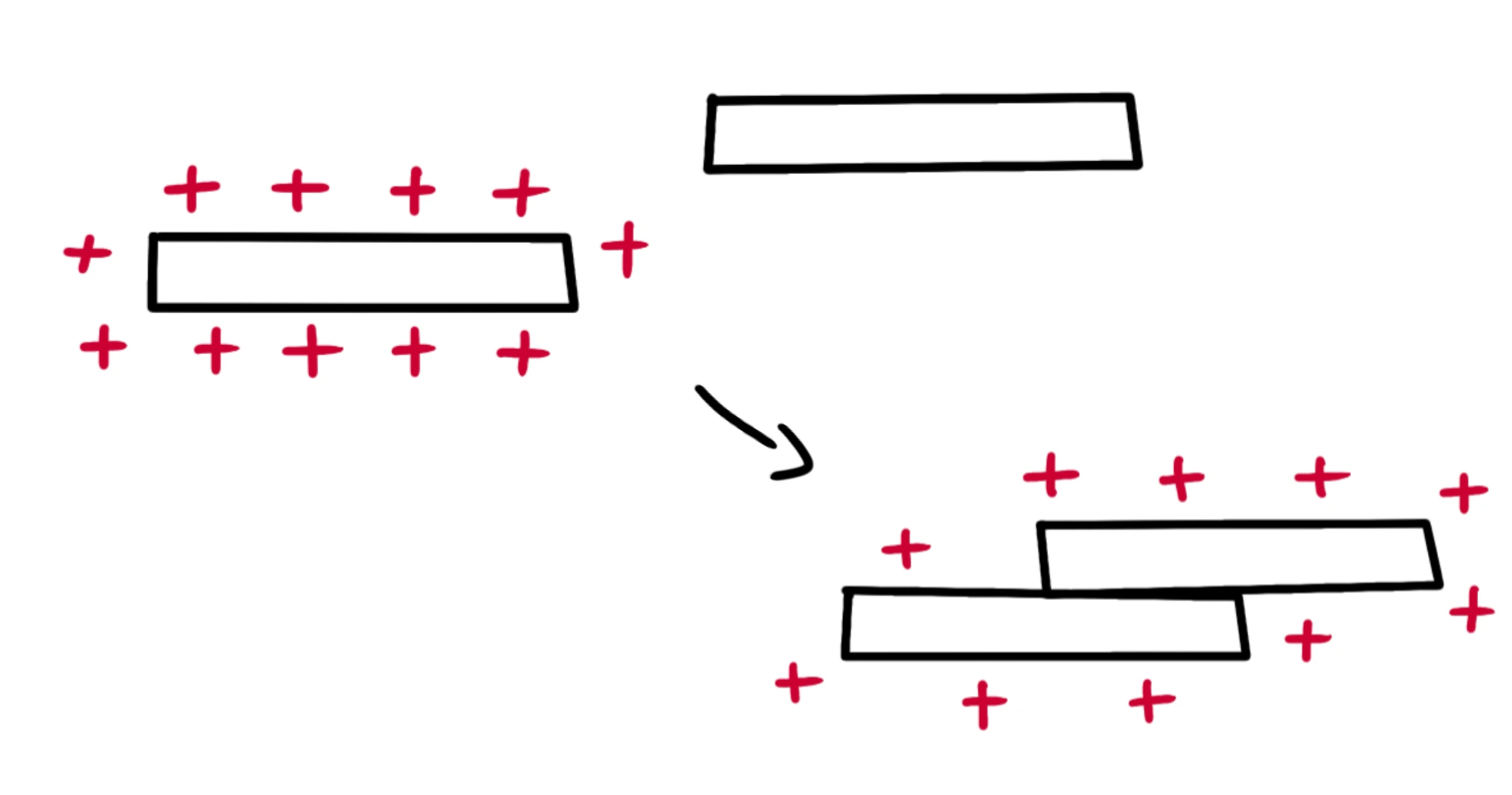
Se il primo conduttore è elettrizzato positivamente, il secondo verrà caricato positivamente perché cederà parte dei suoi elettroni al conduttore che ne ha una mancanza:

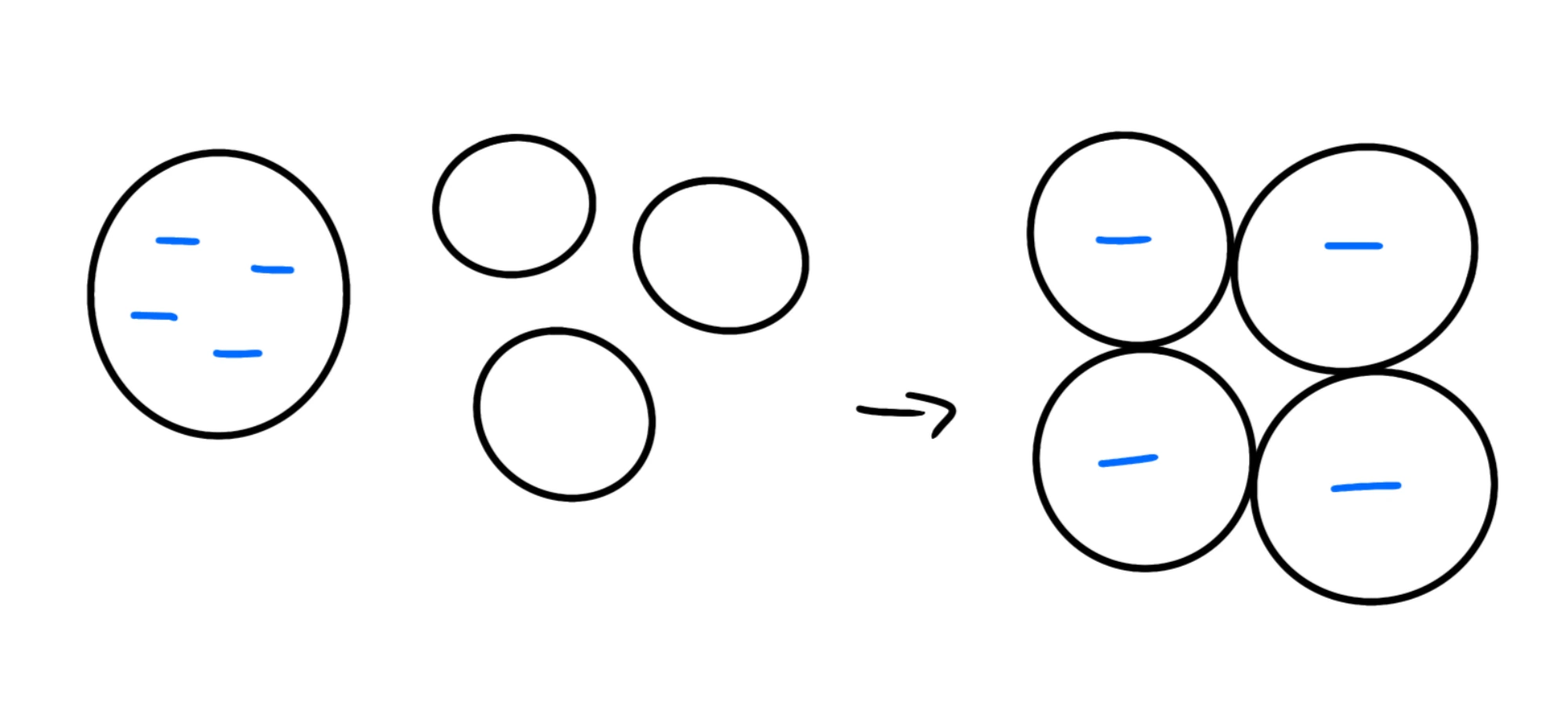
Se prendiamo dei corpi uguali, uno dei quali è caricato elettricamente, e li mettiamo in contatto, la carica si distribuirà ugualmente in tutti i corpi:

Per caricare un conduttore, non c'è bisogno che i due corpi entrino in contatto: possiamo anche elettrizzarlo per induzione.

Prendiamo come prima un corpo carico positivamente ed un conduttore. Ora avviciniamo i due corpi senza però farli toccare:

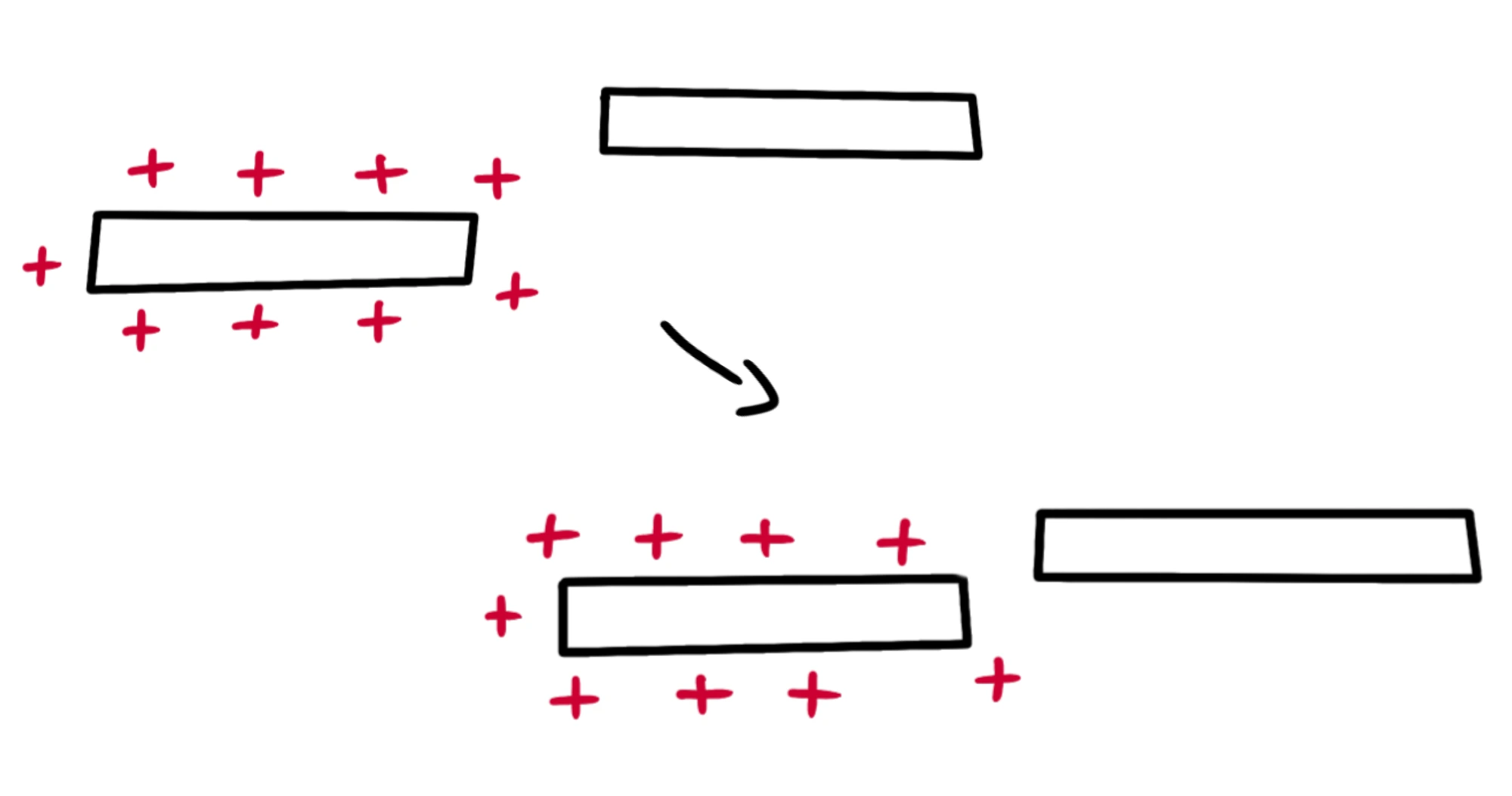
Gli elettroni nel conduttore sono liberi di muoversi e saranno attratti dalla carica positiva dell'altro corpo. Per questo si sposteranno verso sinistra e cambieremo la distribuzione delle cariche, rendendo la parte sinistra carica negativamente e quella destra positivamente:

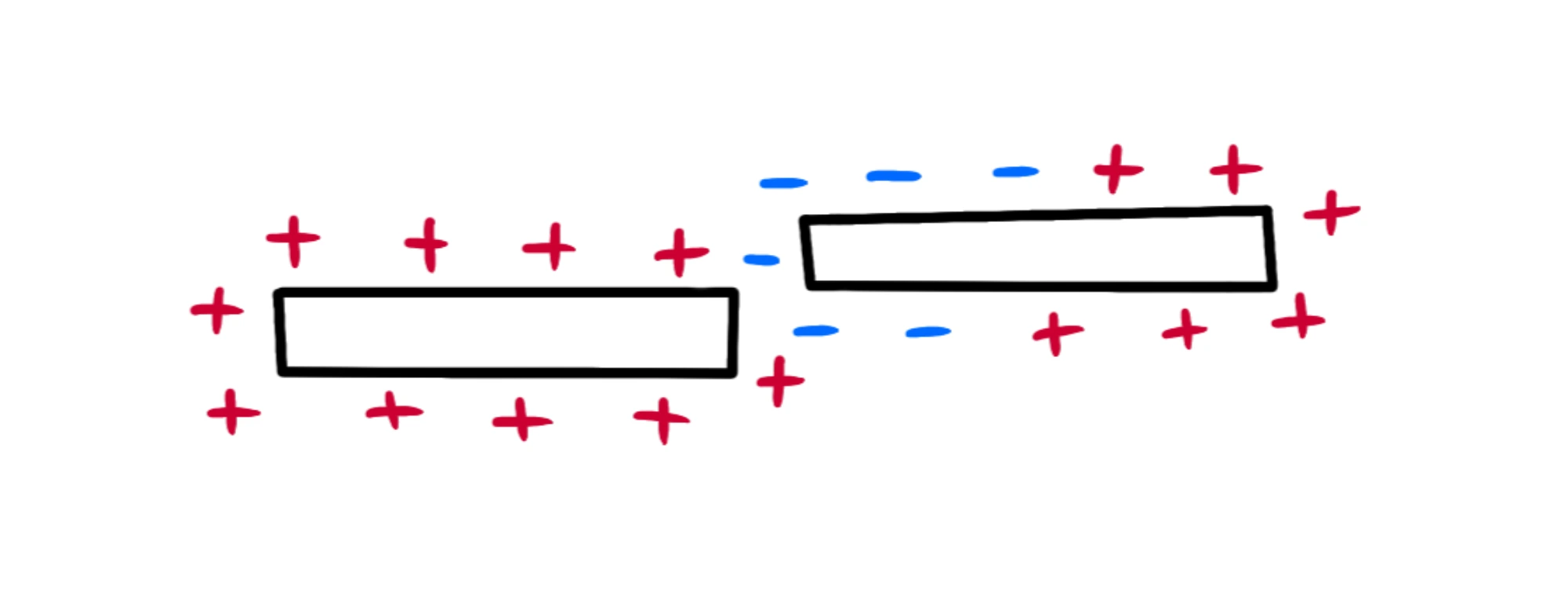
Ora il corpo, nel suo complesso, è rimasto neutro: abbiamo solo cambiato la dispozione delle cariche. Per caricarlo effettivamente, posso toccare l'estremità negativa per far passare gli elettroni nel mio corpo. In questo modo il secondo conduttore sarà stato caricato positivamente:

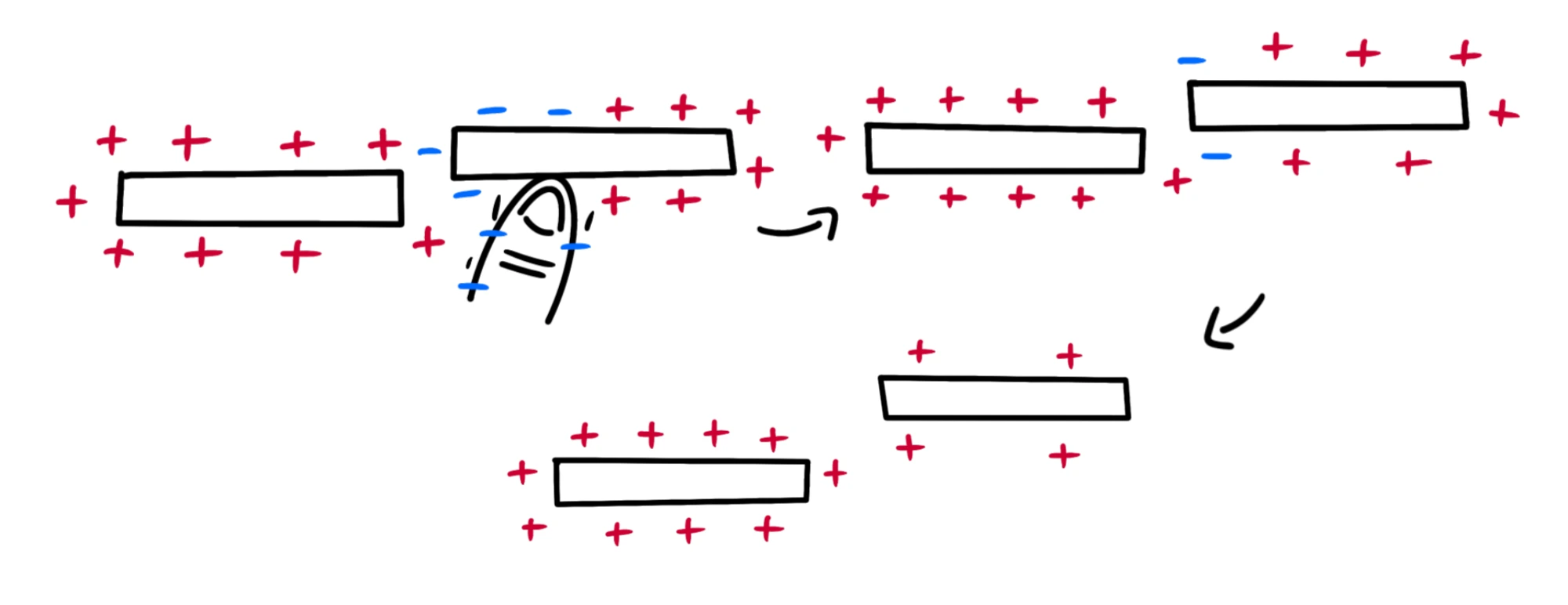
La legge di Coulumb

La forza di attrazione o di repulsione tra due cariche elettriche Q_1 e Q_2 non è casuale, ma si può calcolare tramite la legge di Coulumb:

Se chiamiamo F il modulo forza elettrica e r la distanza tra le due cariche abbiamo:

F = k_0 {|Q_1Q_2|\over r^2}

Dove k_0 è una costante che vale circa 8,99\cdot 10^9 {Nm^2\over C^2}.

Una forza è un vettore, dunque oltre ad un modulo deve anche avere una direzione e un verso. Come per la forza di gravità, la direzione della forza elettrica è la retta che congiunge i centri delle due cariche. Il verso, invece, dipende dal segno delle cariche, come abbiamo visto nei capitoli precedenti:

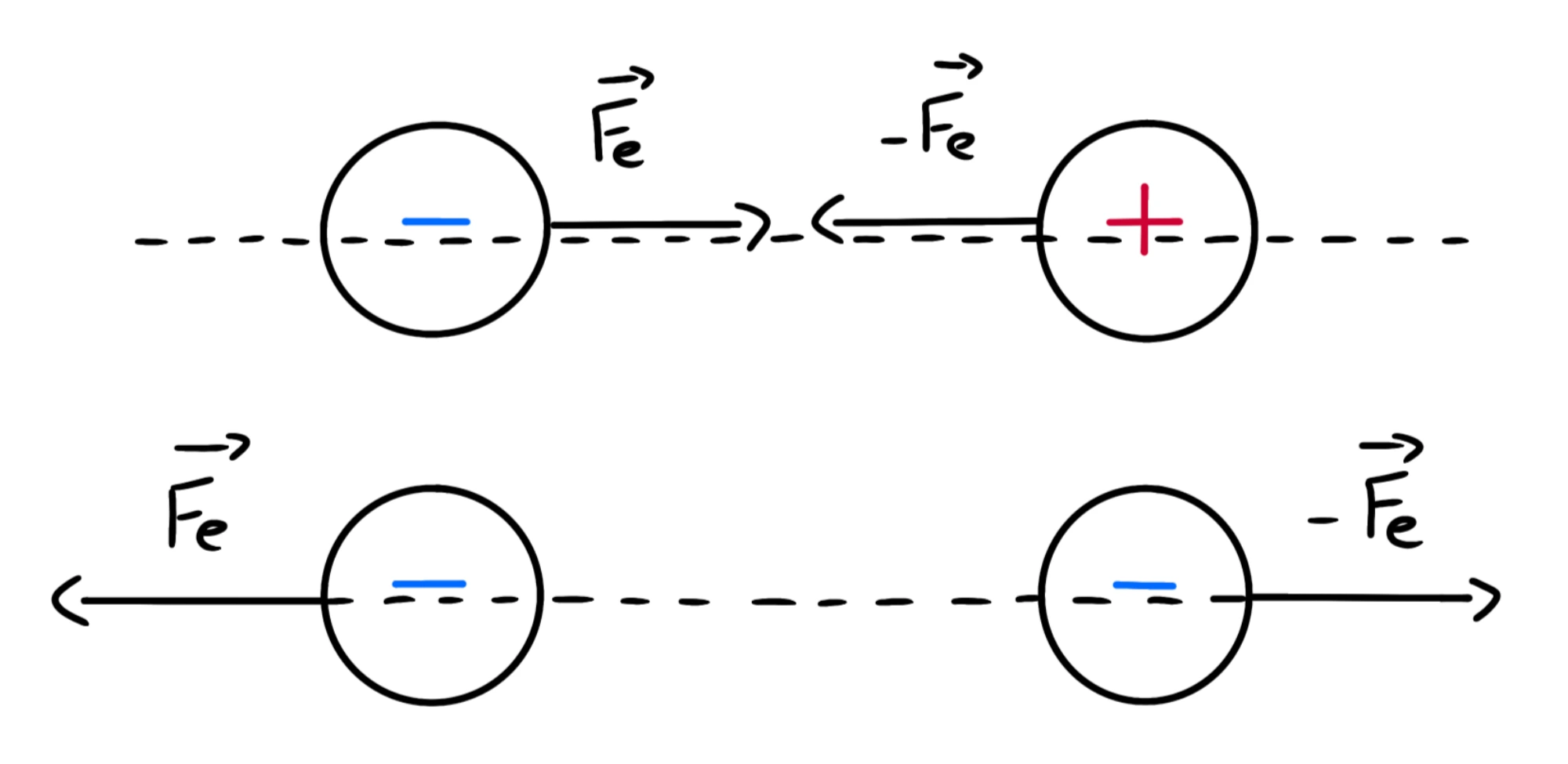
E' importante notare che il modulo della forza che la prima carica applica sulla seconda è uguale a quello della forza che la seconda applica alla prima.

Notiamo poi che la forza elettrica rispetta il terzo principio della dinamica perché, essendo le due uguali ma di segno opposto, la loro somma è 0.

Spesso, siccome gli esperimenti sono solitamente fatti con sfere, conviene usare {1\over 4\pi k_0} al posto di k_0. Chiamiamo questa quantità la costante dielettrica del vuoto e si indica con \epsilon_0 (epsilon 0). Abbiamo dunque:

{1\over 4\pi k_0} = \epsilon_0

k_0 = {1\over 4 \pi \epsilon_0}

Sostituendo nella legge di Coulomb abbiamo quindi:

F = {1\over 4 \pi \epsilon_0} {|Q_1Q_2|\over r^2}

\epsilon_0 vale all'incirca 8,854 \cdot 10^{-12} {C^2\over Nm^2}

Notate che abbiamo chiamato \epsilon_0 come costante dielettrica del vuoto. Questo perché la forza elettrica dipende dal mezzo in cui si trovano le due cariche.

Ogni mezzo possiede una propria costante dielettrica relativa \epsilon_r che si può calcolare come il rapporto tra la forza elettrica nel vuoto F_0 e quella nel mezzo F:

\epsilon_r = {F_0\over F}

Siccome la forza elettrica in un mezzo è sempre minore di quella che le stesse cariche avrebbero alla stessa distanza nel vuoto, la costante dielettrica relativa è sempre maggiore di 1 (o uguale ad 1 se stiamo nel vuoto).

Dalla definizione di \epsilon_r possiamo trovare quanto vale la forza elettrica F quando le due cariche sono immerse in un mezzo:

\epsilon_r = {F_0 \over F}

F = {F_0 \over \epsilon_r}

F = {{1\over 4\pi\epsilon_0} {|Q_1Q_2|\over r^2}\over \epsilon_r}

F = {1\over 4\pi \epsilon_0 \epsilon_r} {|Q_1Q_2|\over r^2}

Per semplificare la scrittura ed i calcoli, chiamiamo il prodotto \epsilon_0 \epsilon_r "costante dielettrica assoluta del mezzo" e la indichiamo con \epsilon . Così otteniamo la forma finale della legge di Coulomb:

F = {1\over 4 \pi \epsilon} {|Q_1Q_2|\over r^2}

Negli esercizi, siccome la costante dielettrica relativa dell'aria è circa uguale ad 1, se le cariche si trovano in aria, potete comunque ignorare l'effetto dell'aria e comportarvi come se fossero nel vuoto.

Se però le cariche si trovano in altri mezzi con costanti elettriche relative non approssimabili ad 1, bisogna tenere conto di questo fatto utilizzando la costante dielettrica assoluta al posto di \epsilon_0.

Forza elettrica VS Forza di gravità

Guardiamo il rapporto tra la forza elettrica e quella di gravità tra un protone ed un elettrone nel vuoto:

Ricordiamo che i valori assoluti delle cariche e del protone e dell'elettrone sono uguali e valgono circa 1,6022\cdot 10^{-19}C, che \epsilon_0 vale circa 8,854 \cdot 10^{-12}{C^2\over Nm^2} e che la costante di gravitazione universale G vale circa 6,67 \cdot 10^{-11} {Nm^2\over kg^2}. Infine, le masse del protone e dell'elettrone valgono rispettivamente m_p= 1,67\cdot 10^{-27} kg e m_e= 9,1\cdot 10^{-31}kg.

Possiamo ora calcolare il rapporto tra le due forze:

{F_e \over F_g } = {{1\over 4\pi\epsilon_0} {e^2\over r^2}\over G{m_p m_e\over r^2}}= {e^2\over 4\pi\epsilon_0 G m_e m_p}\approx 10^{39}

Cioè la forza elettrica è 10^{39} volte più grande di quella di gravità. Per questo quando stiamo studiando le interazioni tra protoni ed elettroni possiamo trascurare la forza di gravità.