Campo elettrico

Cosa devo già sapere?

Da sapere:

Cariche elettriche

Forza di Coulomb

Cos'è il campo elettrico?

Quando prendiamo due cariche elettriche, abbiamo detto che la prima esercita un forza sulla seconda e la seconda sulla prima.

Prendiamo ora una carica elettrica positiva Q:

Se ora prendiamo un'altra carica positiva q e la mettiamo nel punto P, la prima applicherà una forza su di essa. Pensiamo di fissare la prima carica in maniera che stia ferma.

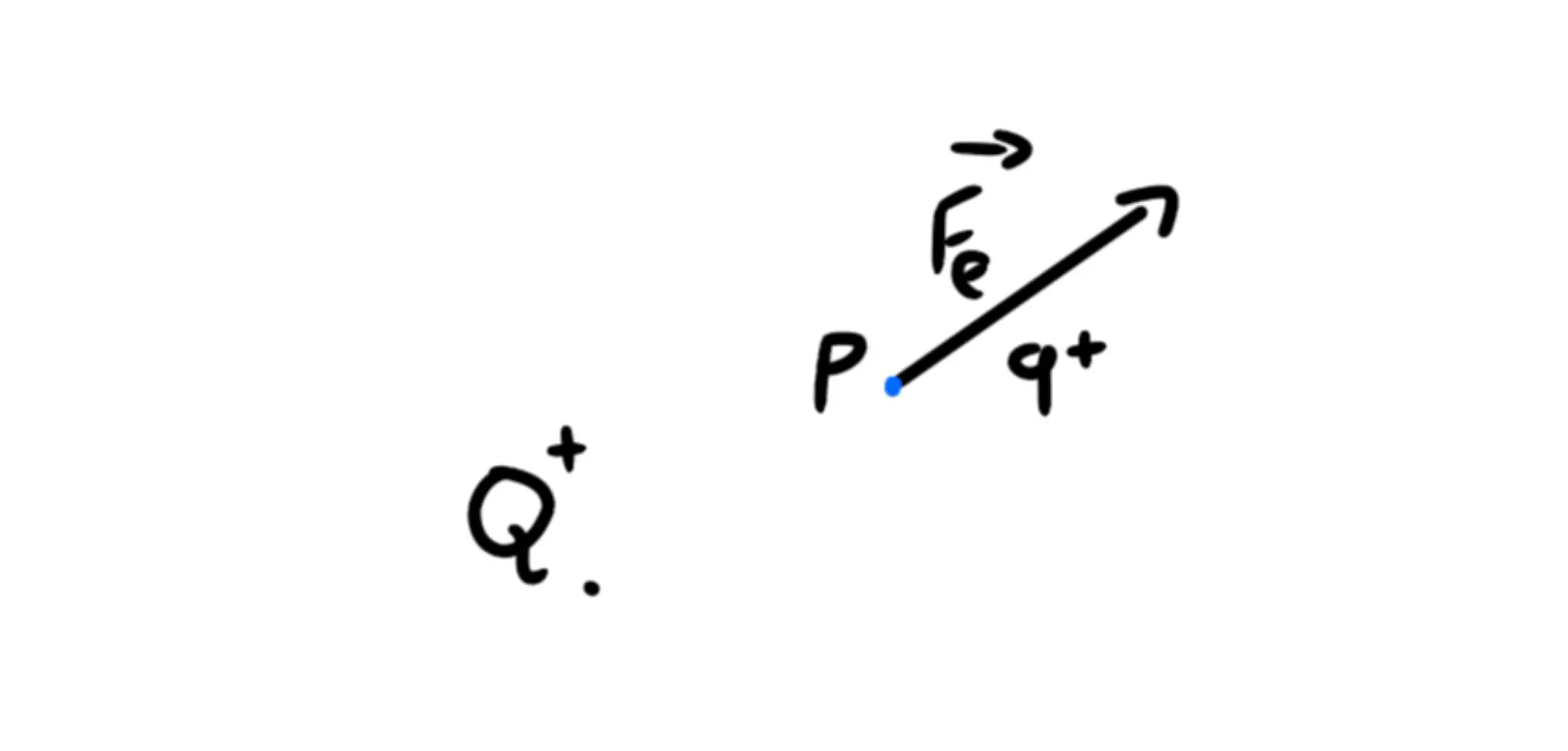
Questa forza che gli viene applicata, non dipende solo da Q, ma anche da q, perché la legge di Coulomb ci dice che la forza elettrostatica si calcola come F_e = {1\over 4 \pi \epsilon _0} {|Q| |q|\over r^2}.

Quindi la forza elettrica da sola non ci aiuta a descrivere molto la particella.

Vogliamo ottenere qualcosa che dipenda soltanto dalla prima carica. Come fare? Possiamo dividere il tutto per la carica della seconda particella, q.

In questo modo otteniamo {F\over q} che è uguale a {1\over 4\pi \epsilon _0} {|Q|\over r^2}. Definiamo questo come il modulo del campo elettrico E(P) generato da Q nel punto P in cui si trova q:

E(P) = {F\over q}

E(P) = {{1\over 4 \pi \epsilon _0} {|Q|\over r^2}}

L'unità di misura del campo elettrico è il Newton su Coulomb (N/C).

Come misurarlo nella vita reale? Basta fissare la carica di cui vogliamo conoscere il campo. Prendere un'altra carica che deve essere molto piccola affinchè il campo elettrico che quest'ultima induce non interferisca troppo con il primo e infine misurare con un dinamometro la forza che gli viene applicata e dividerla per la carica della seconda pallina.

Il campo elettrico in un punto è un vettore e dunque avrà una direzione ed un modulo. Essi sono gli stessi della forza che viene applicata ad una carica positiva in quel punto. Nel nostro caso, dunque, \overrightarrow{E} sarà il seguente vettore:

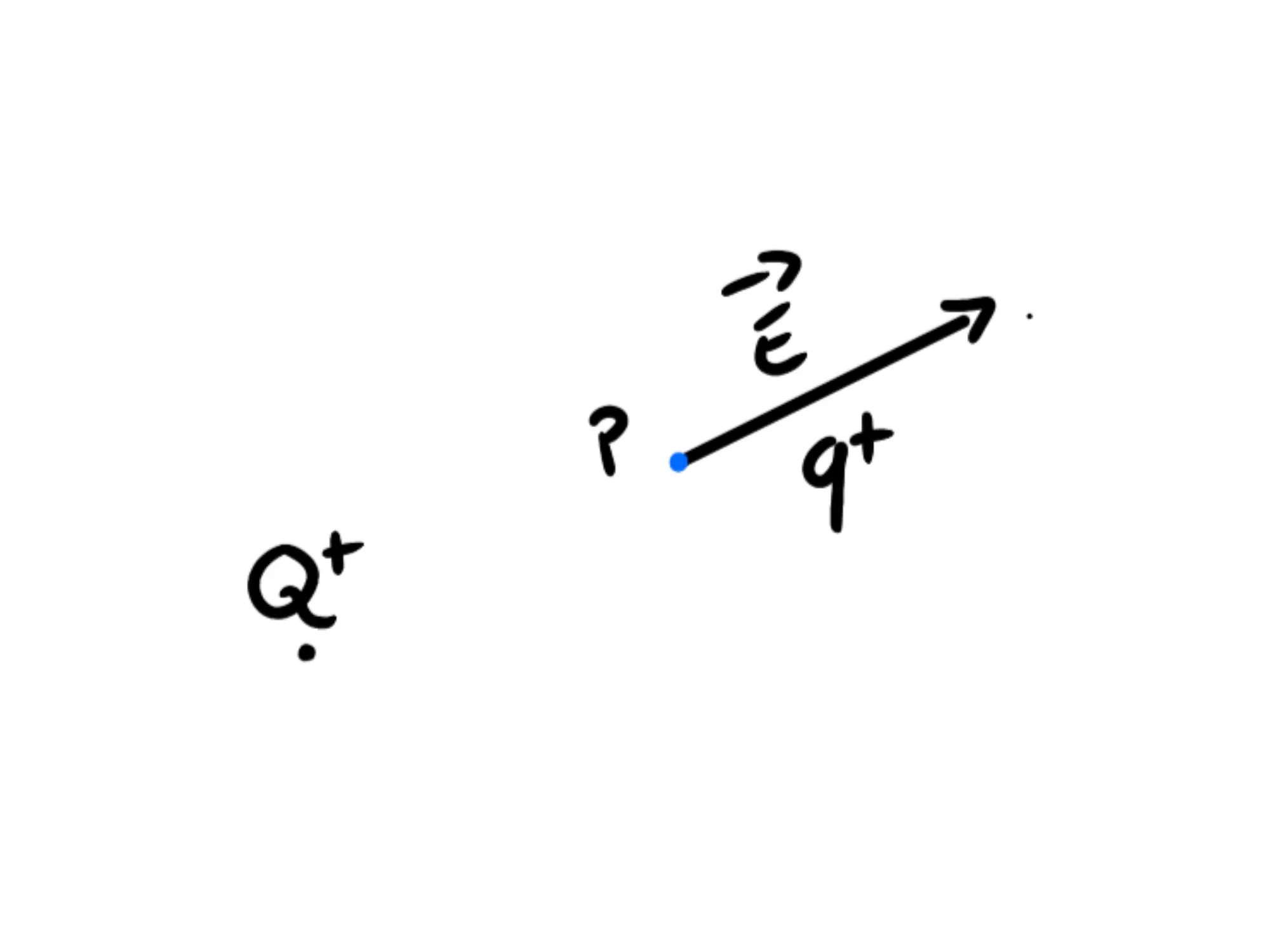
Adesso immaginiamo di porre in tanti altri punti delle piccole cariche positive e di usare quest'ultime per trovare il campo elettrico in quei punti.

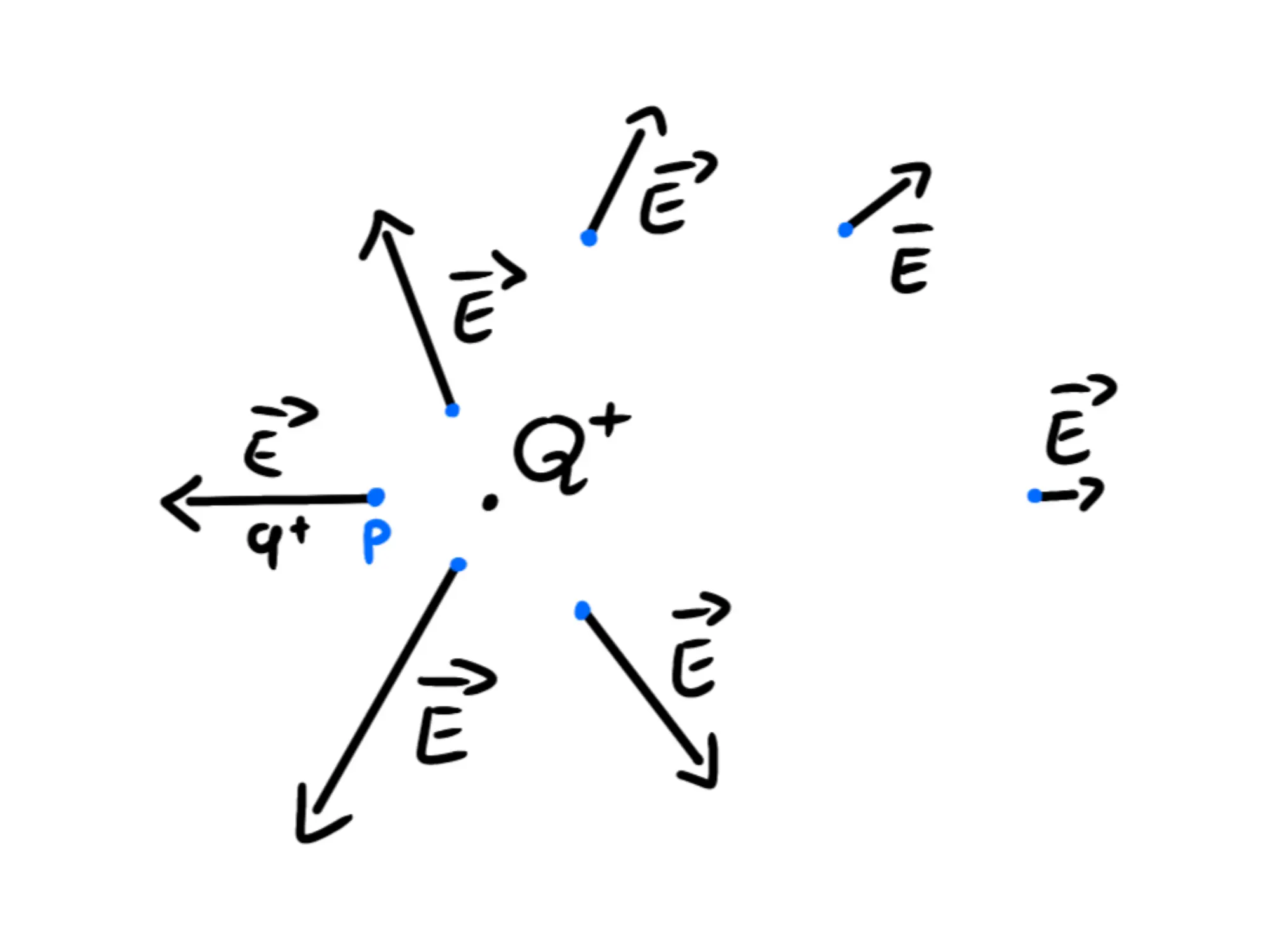
Ad ogni punto che prendiamo, dunque, gli associamo un vettore. Ora pensiamo di prendere sempre più punti, sempre più punti, finchè non abbiamo preso tutti i punti dello spazio.

Ad ogni punto, quindi, sarà associato un vettore, che sarà proprio il campo elettrico in quel punto.

Quello che abbiamo appena creato è il campo elettrico generato da Q.

E' impossibile visualizzare il campo elettrico nel suo intero usando le freccie per i vettori, perché, oltre al fatto che è difficile pensare a infiniti punti, dopo un po' si sovrapporrebbero tantissime freccie e sarebbe un casino.

Dovete dunque capire il concetto e disegnare giusto una manciata di vettori nel vostro disegno perché sennò diventa incomprensibile.

Ok, ma a cosa serve questo campo?

Entro qualche settimana scoprirete che è utilissimo in moltissime situazioni, ma vi anticipiamo già il concetto di fondo che sta dietro al perché usare il campo elettrico:

Prima, quando avevamo due particelle cariche, dicevamo che la prima interagiva direttamente con la seconda e viceversa.

Ora il campo elettrico funge da intermediario. Non diremo più che la prima interagisce direttamente con la seconda, ma che la prima induce un campo elettrico che interagisce con la seconda e viceversa.

Cioè siamo passati da una relazione del seguente tipo:

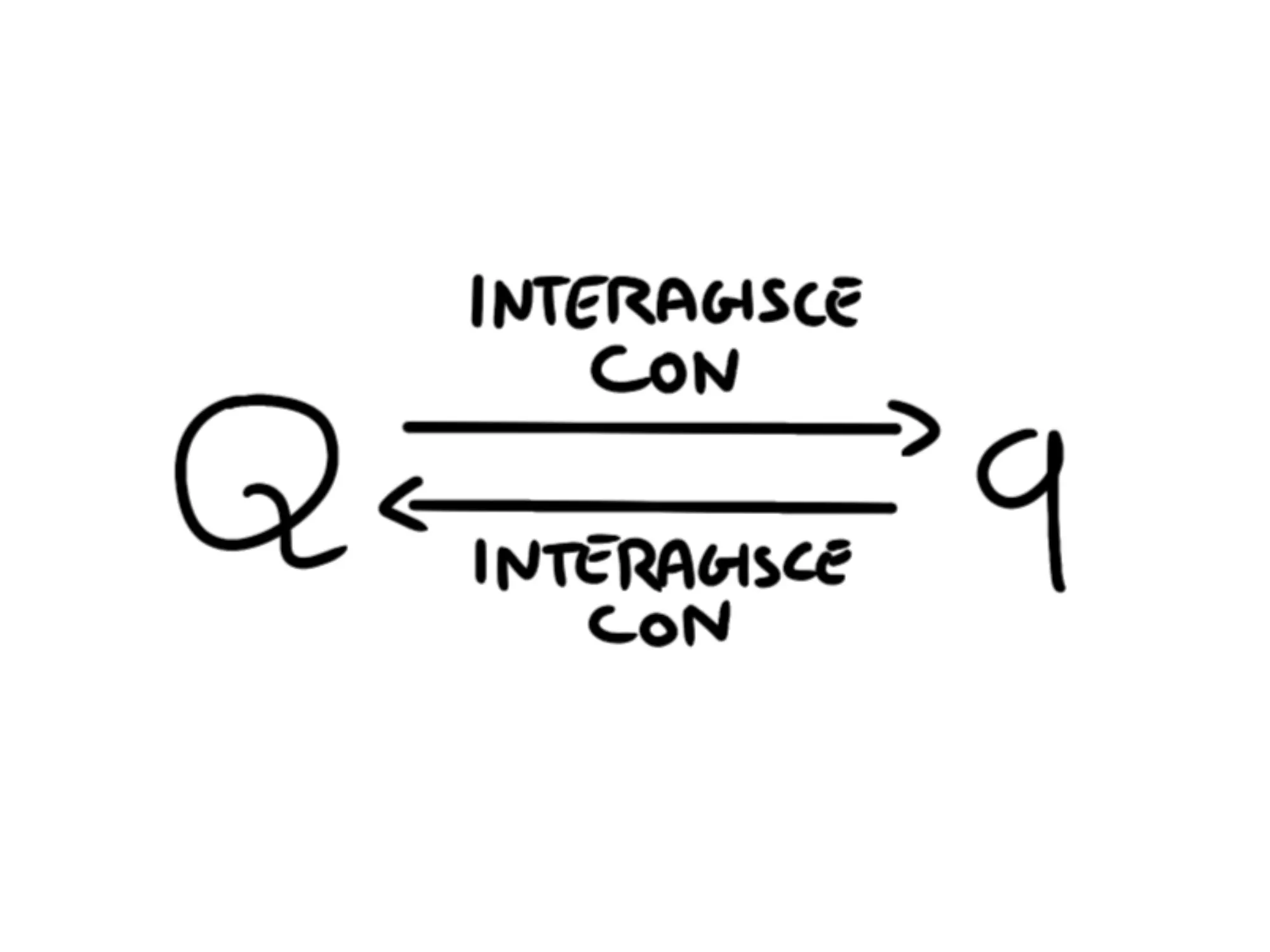
Alla seguente:

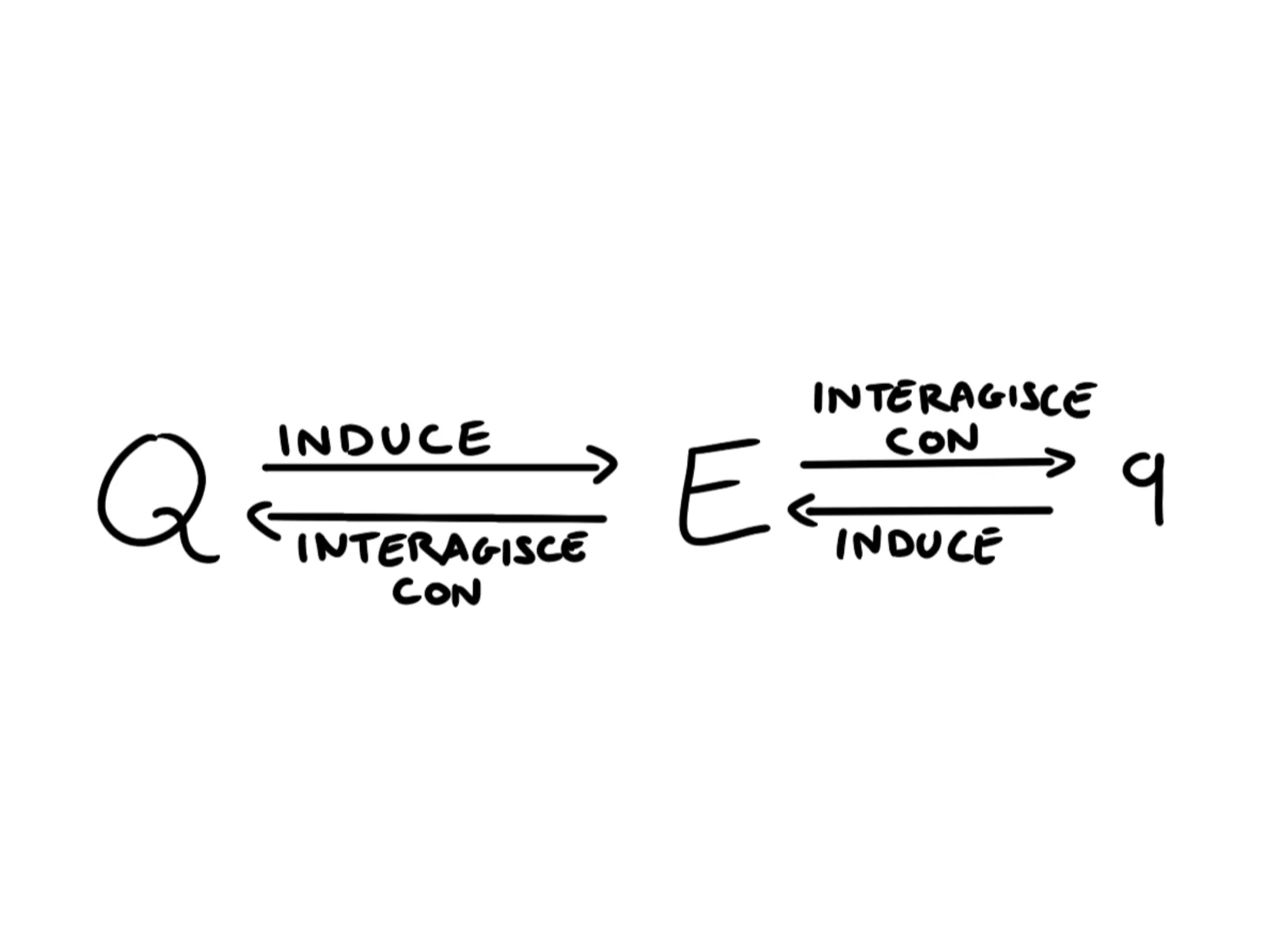
Lo so che può sembrare tutta roba inutile, ma fidatevi che tra qualche mese avrete capito quanto è utile, per tutte le volte che lo avrete usato per risolvere i problemi.

Come avete visto nei grafici precedenti, il campo elettrico di una carica positiva è formato da vettori che puntano lontano dalla carica:

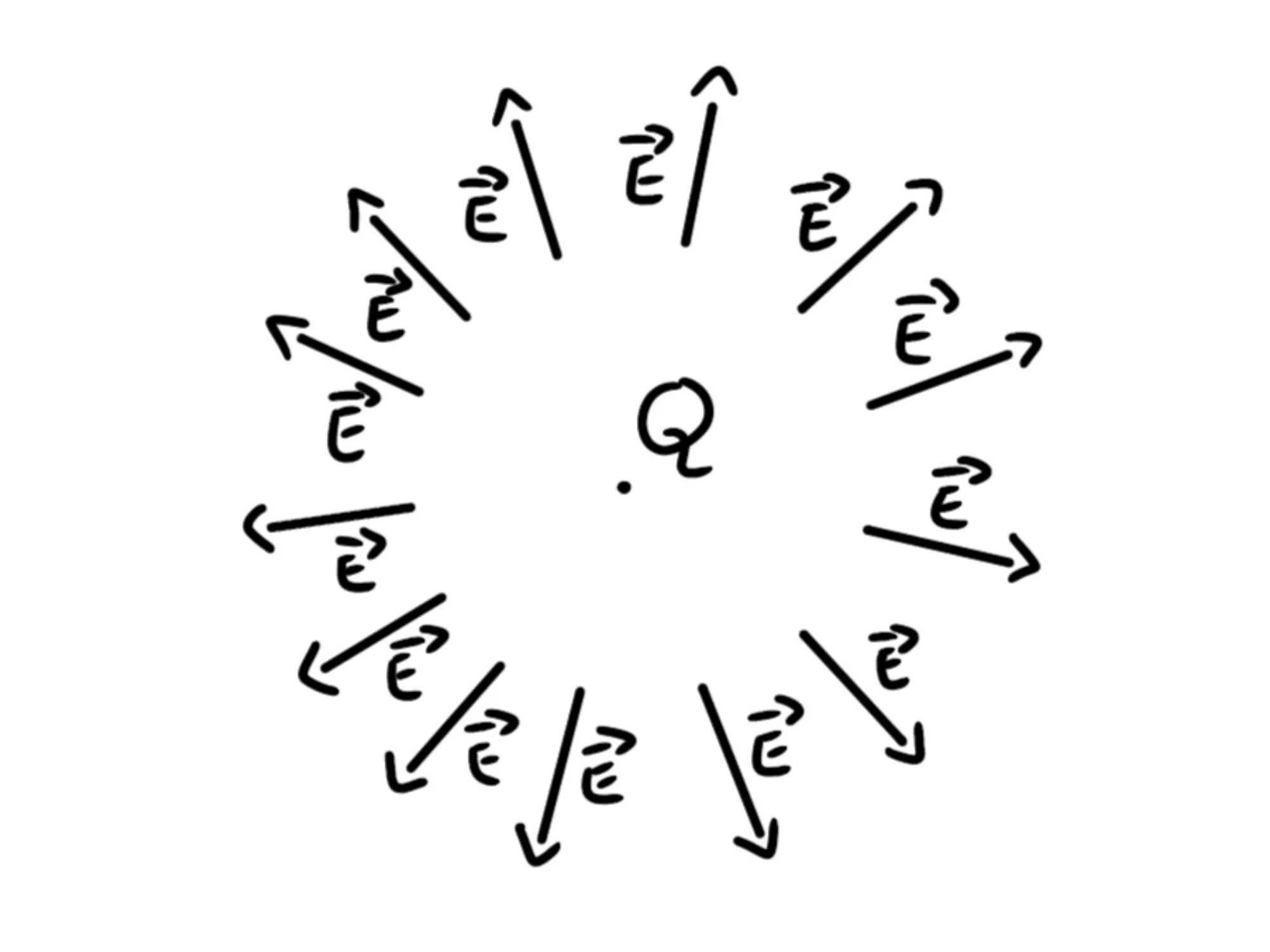
Siccome abbiamo detto che E = {1\over 4\pi\epsilon _0}{|Q| \over r^2}, il modulo del campo elettrico è inversamente proporzionale al quadrato di r, che sarebbe la distanza dalla carica Q. Quindi più ci allontaniamo e più E diminuisce.

Se invece di avere una carica positiva Q ne abbiamo una negativa, sarà tutto uguale tranne il verso dei vettori del campo elettrico, che sarà opposto:

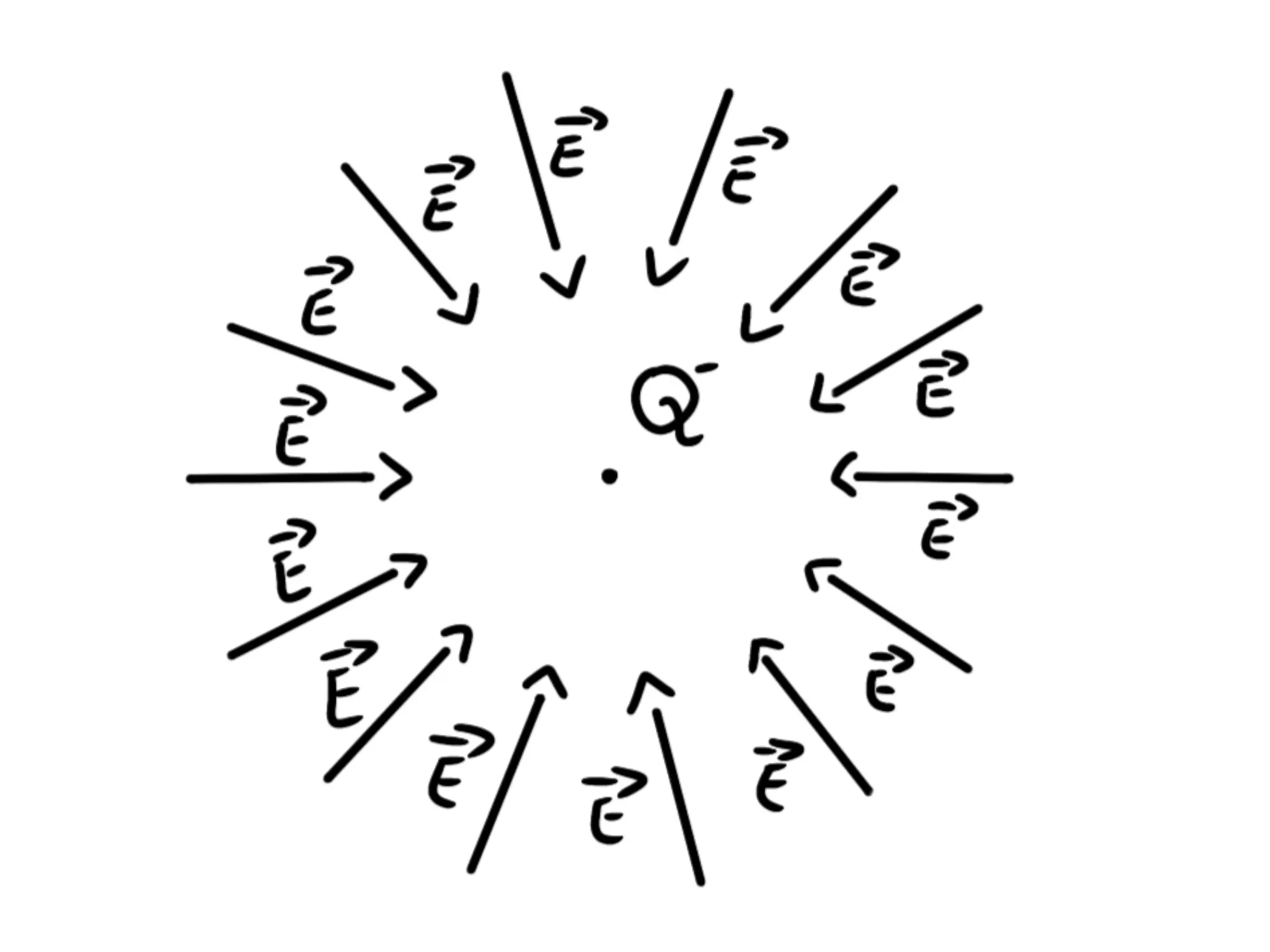
Cioè i vettori puntano verso la carica.

Siamo a un buon punto, sappiamo quasi tutte le informazioni base del campo elettrico, ci manca solo la studiare le linee di campo.

Che sono? In pratica posso tracciare delle linee che sono tangenti ai vettori del campo elettrico (o che li contengono se sono tutti allineati come nel nostro caso).

E infine metto una freccetta sulla linea per indicare il verso del campo.

Ecco il campo della carica positiva di prima raffigurato mediante le linee di campo:

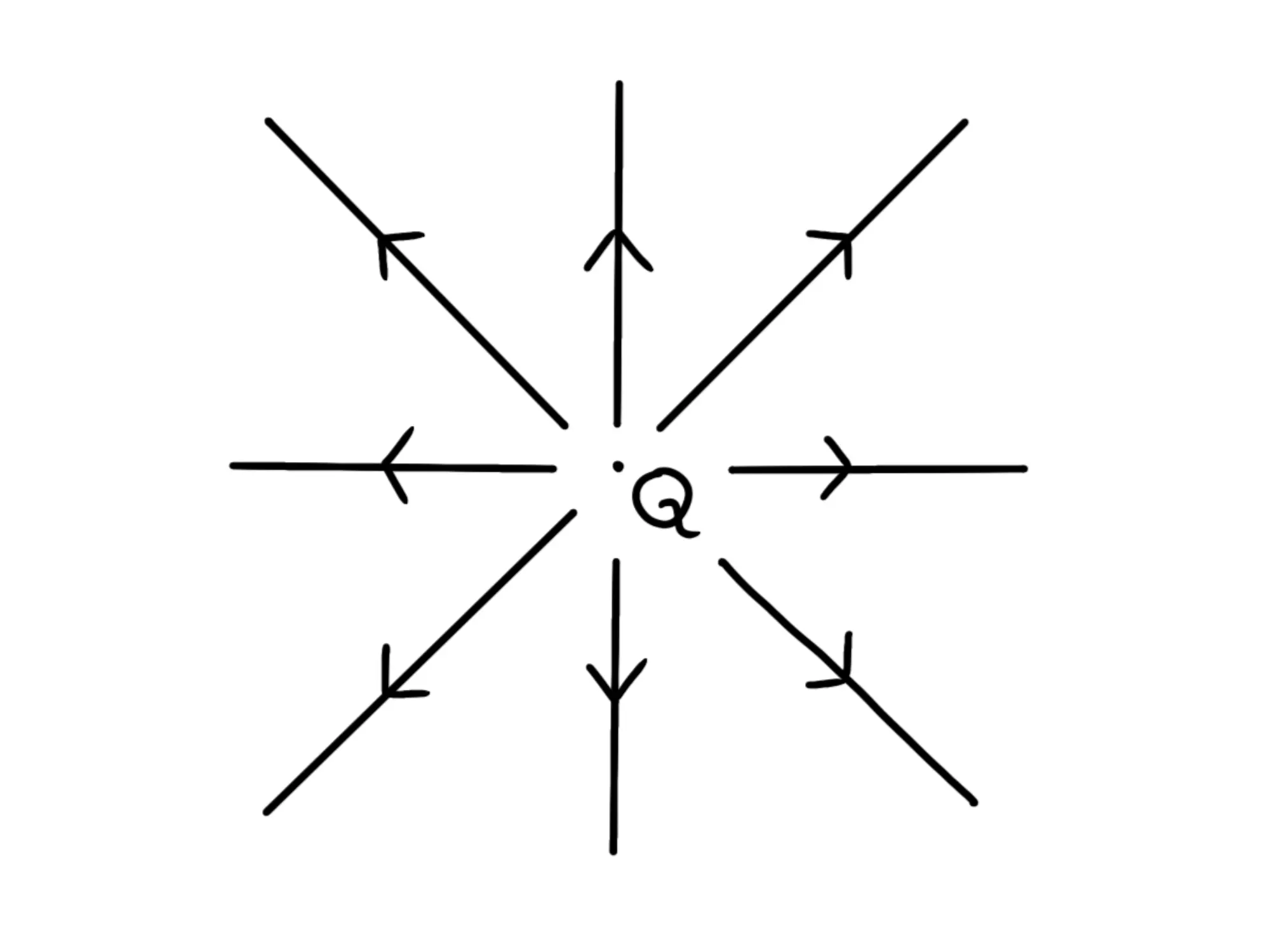
Però, siccome ho infiniti vettori in infinite direzioni diverse, ho anche infinite linee di campo. Quindi quante ne metto? Ne mettiamo un po', né troppe né troppo poche. Inoltre, scegliamo il numero di linee del campo sarà proporzionale alla carica della particella che lo genera se abbiamo più particelle. Cioè, se ho un primo corpo con carica 1C e traccio il suo campo elettrico usando 4 linee, se nello stesso problema devo raffigurare quello generato da una carica da 3C (cioè 3 volte maggiore) disegnerò 12 linee di campo (cioè il triplo).

Se la carica è negativa, il verso delle linee sarà entrante nella carica:

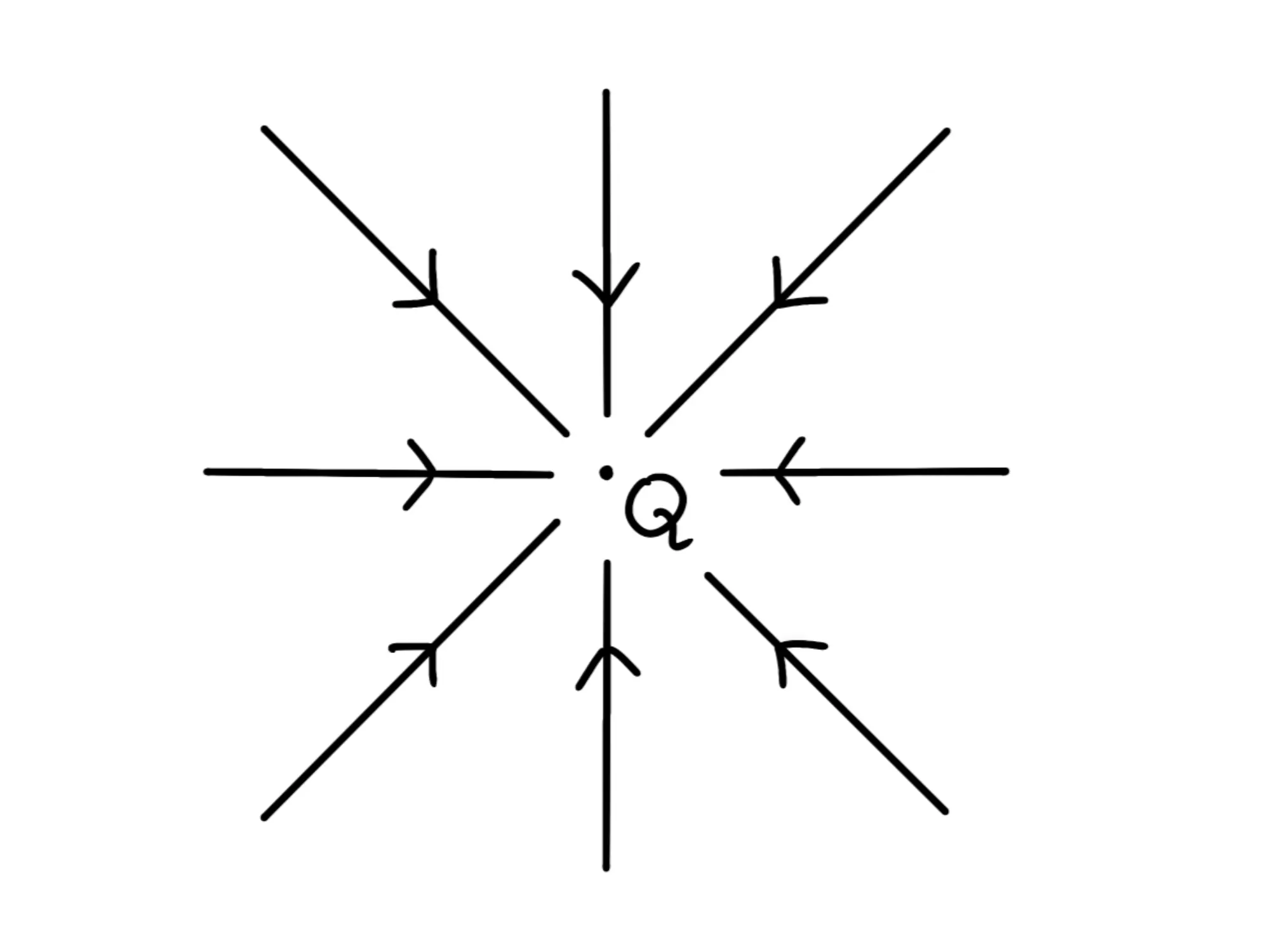
Quindi le linee di campo sono sempre uscenti dalle cariche positive ed entranti in quelle negative.

Più campi elettrici

Se abbiamo più cariche possiamo ottenere campi elettrici molto più complicati. Ne vedremo di vari tipi, ma per ora ci soffermiamo al caso più semplice e al caso del campo di un dipolo.

Cos'è il campo di un dipolo? Prima vediamo cos'è un dipolo. Esso è una coppia di cariche elettriche uguali ma di segno opposto. Quindi, per esempio, potremmo avere una carica da 1C e una da -1C.

Quindi in generale sarà fatto così:

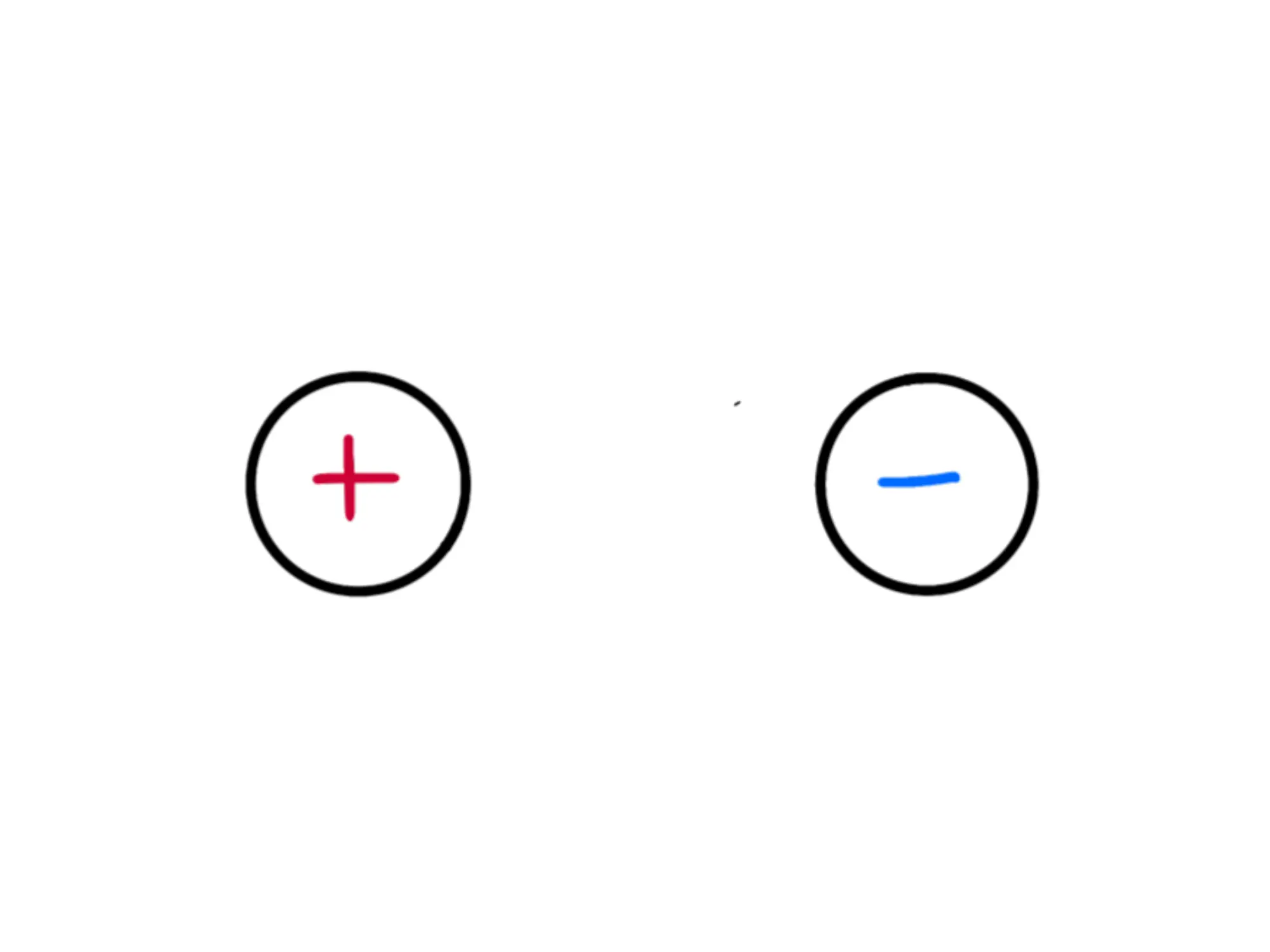
La carica positiva indurrà un campo elettrico \overrightarrow{E_1} e quella negativa indurrà un campo elettrico \overrightarrow{E_2} e sappiamo come sono fatti, ma cosa otteniamo se li combiniamo insieme?

Ricordiamoci che il campo elettrico in un punto P è uguale alla forza che viene applicata ad una piccola carica positiva q in quel punto divisa per la carica, cioè \overrightarrow{E} = {\overrightarrow{F}\over q}.

Quindi dobbiamo avere che \overrightarrow{E_{tot}} = {\overrightarrow{F_{tot}}\over q} e noi sappiamo benissimo come si calcola la forza totale: basta sommare vettorialmente le singole forze. Perciò:

\overrightarrow{E_{tot}} = {\overrightarrow{F_1} + \overrightarrow{F_2}\over q}

\overrightarrow{E_{tot}} = {\overrightarrow{F_1}\over q} + {\overrightarrow{F_2}\over q}

E per definizione {\overrightarrow{F_1}\over q} e \overrightarrow{F_2} \over q sono proprio \overrightarrow{E_1} ed \overrightarrow{E_2}. Perciò abbiamo:

\overrightarrow{E_{tot}} = \overrightarrow{E_1} + \overrightarrow{E_2}

Cioè i campi elettrici si sommano vettorialmente.

Quindi per trovare il campo elettrico del dipolo in un punto P, troviamo prima il campo elettrico della carica positiva in quel punto, poi quello della negativa e li sommiamo vettorialmente:

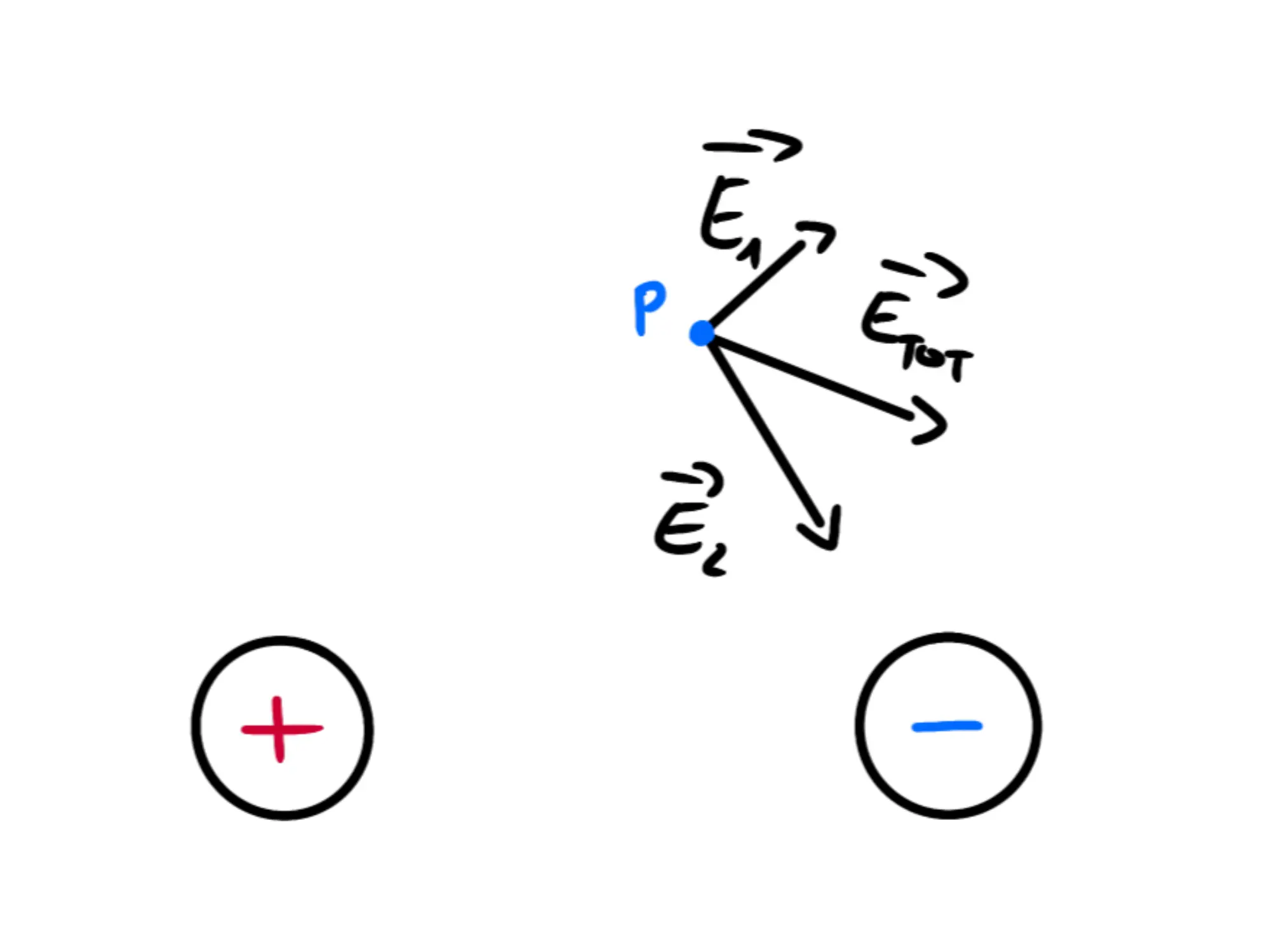
Possiamo prendere molti altri punti e calcolare il campo elettrico in essi:

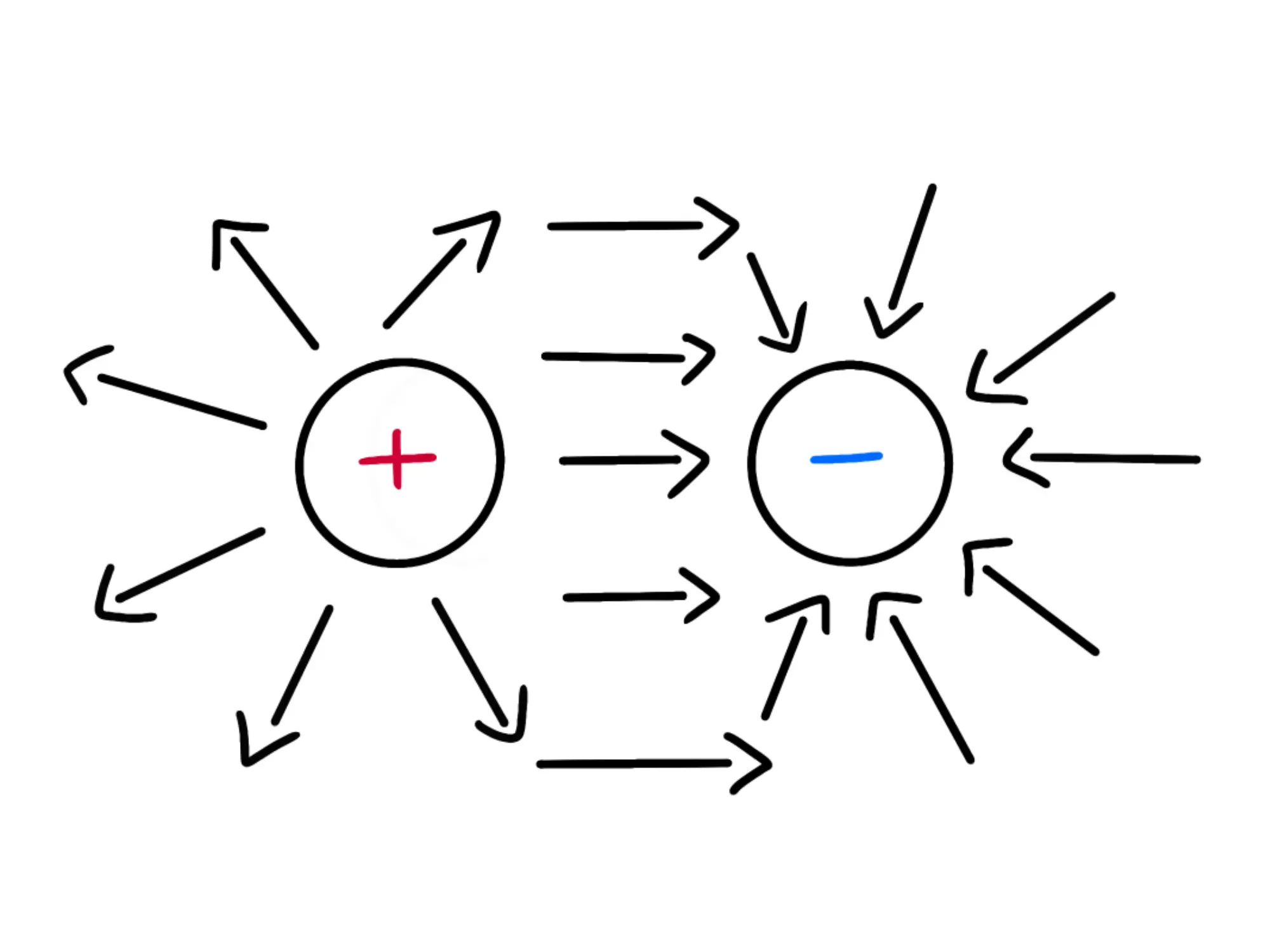
Non è malissimo, ma possiamo renderlo molto più chiaro usando le linee di campo:

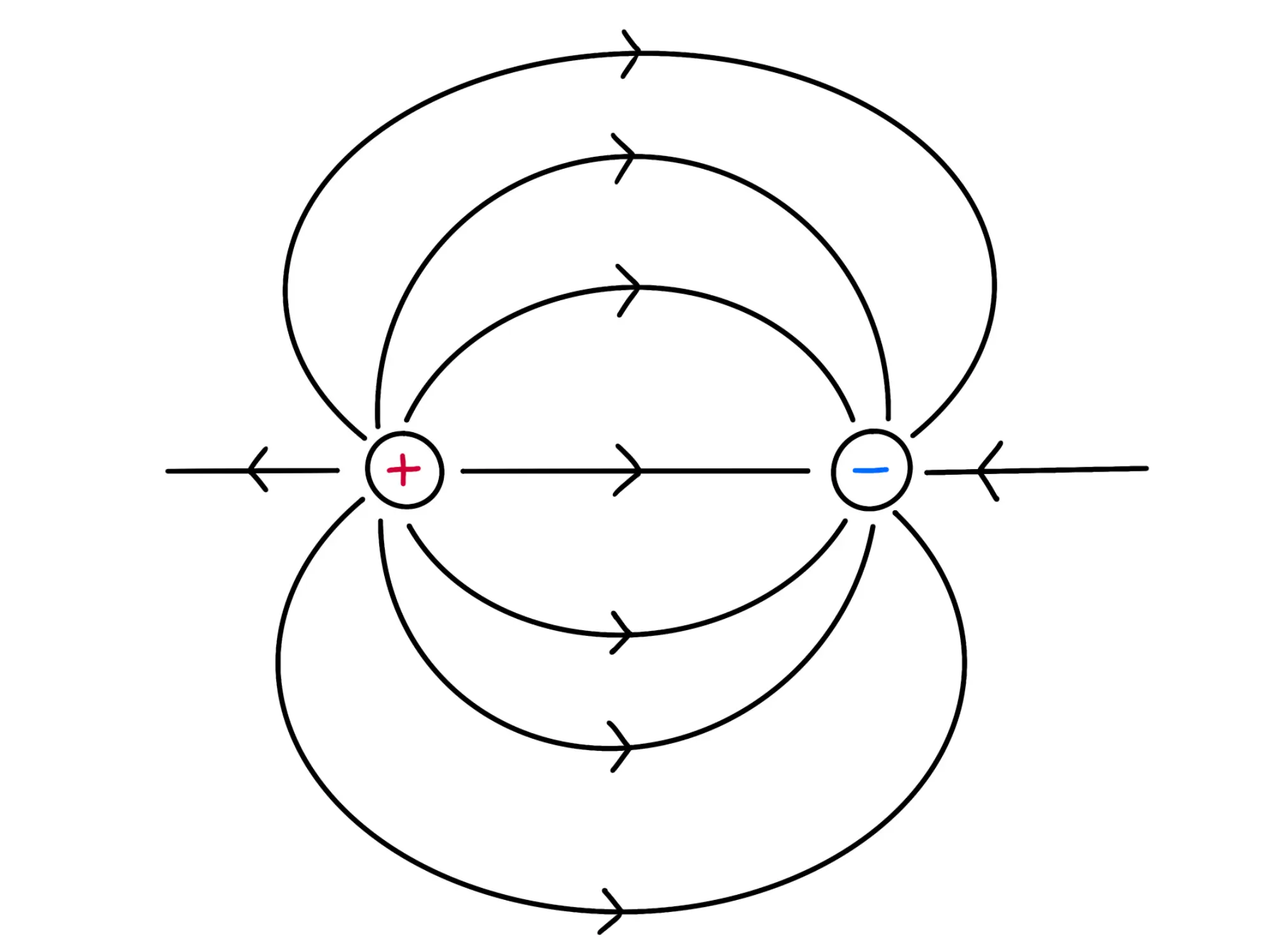
Notiamo che, come avevamo detto nel capitolo precedente, tutte le linee di campo escono dal polo positivo ed entrano in quello negativo.