Triangoli simili

Cosa sono i triangoli simili?

Due triangoli sono detti simili se il primo
è una copia rimpicciolita o ingrandita del secondo. Ad esempio, i due triangoli seguenti sono simili:

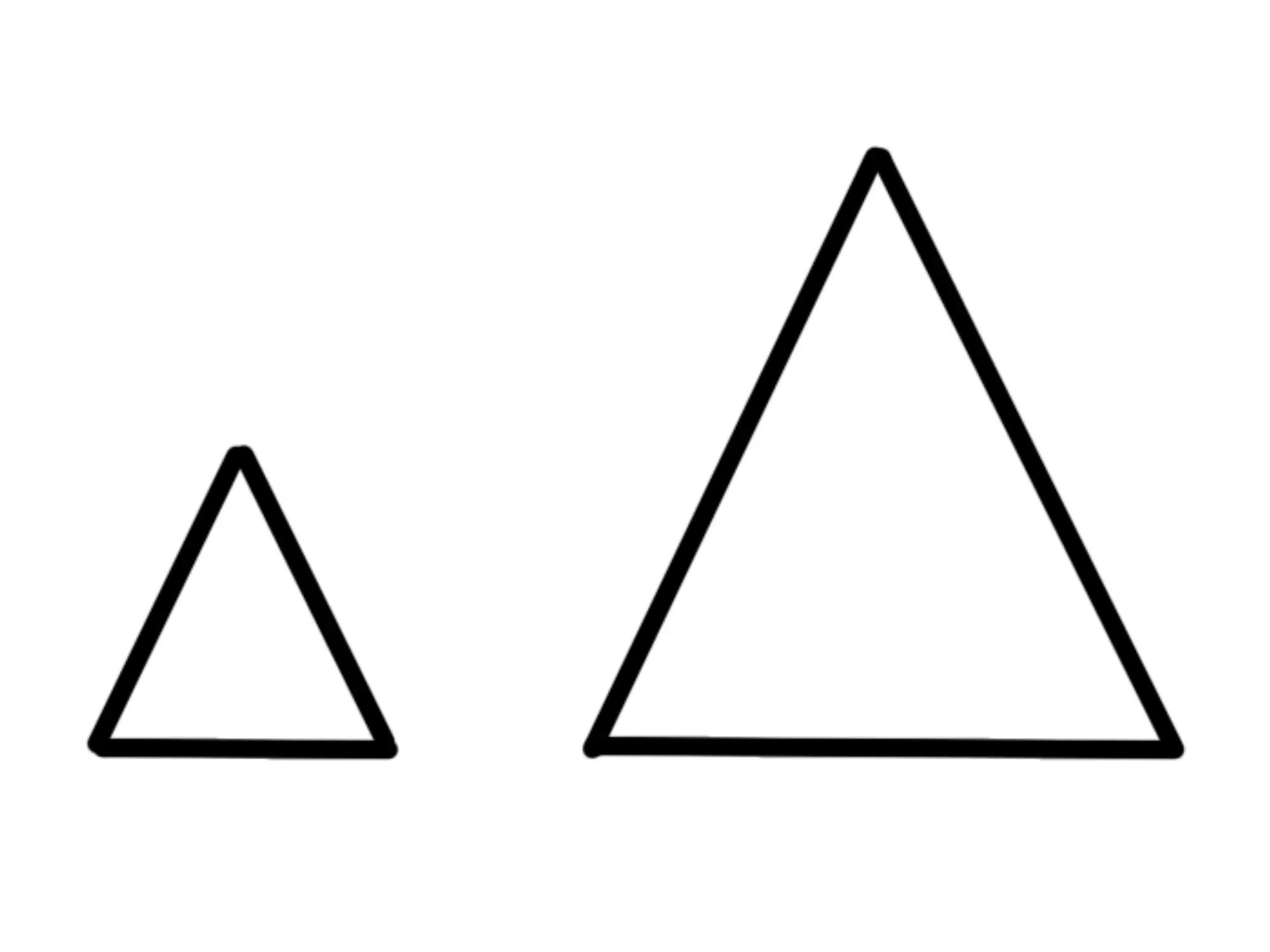
Come per i triangoli congruenti, possono essere ruotati, ribaltati e traslati. Quindi anche i due triangoli seguenti sono simili:

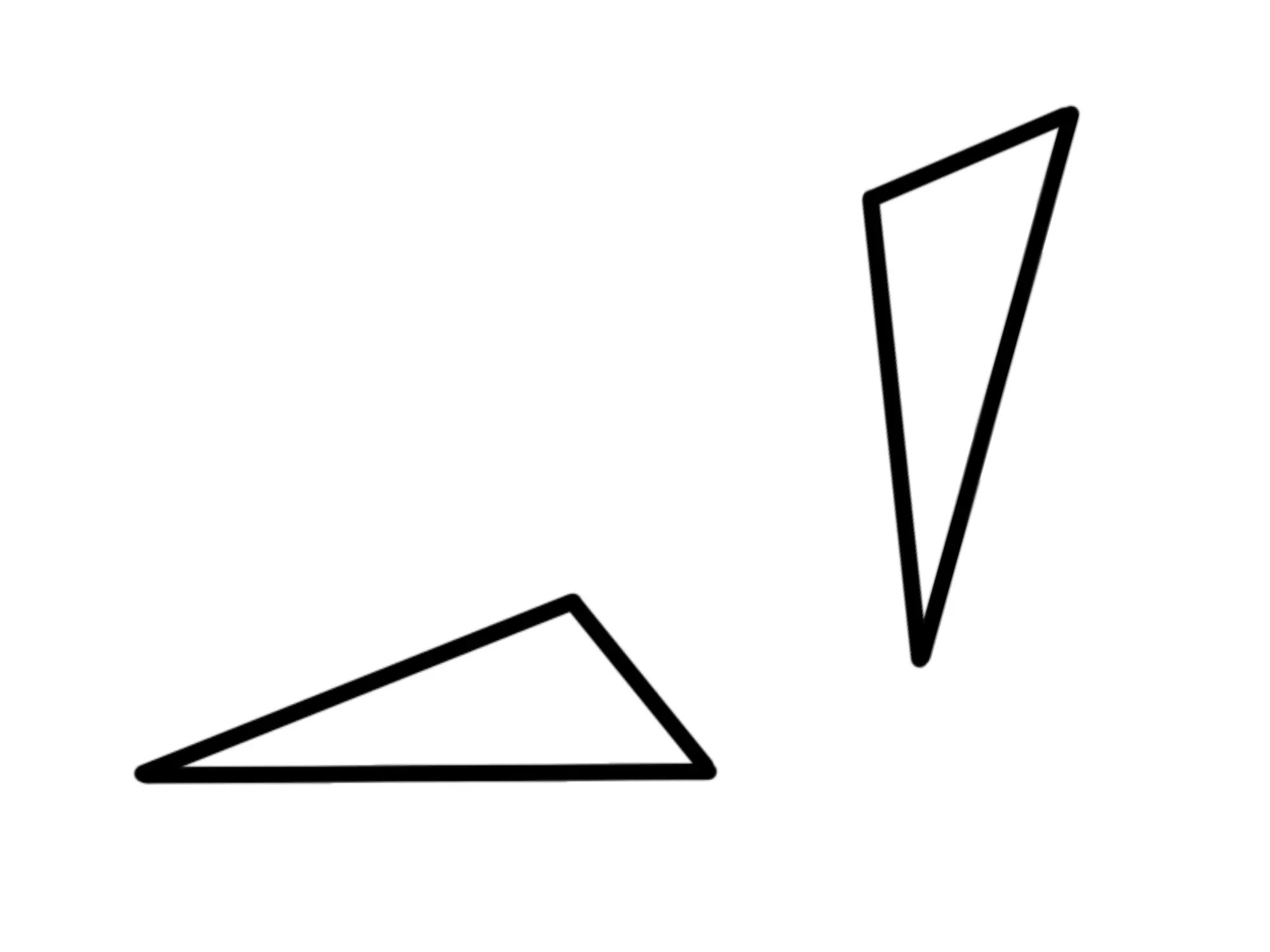
Due triangoli simili devono avere tutti gli angoli rispettivamente congruenti:

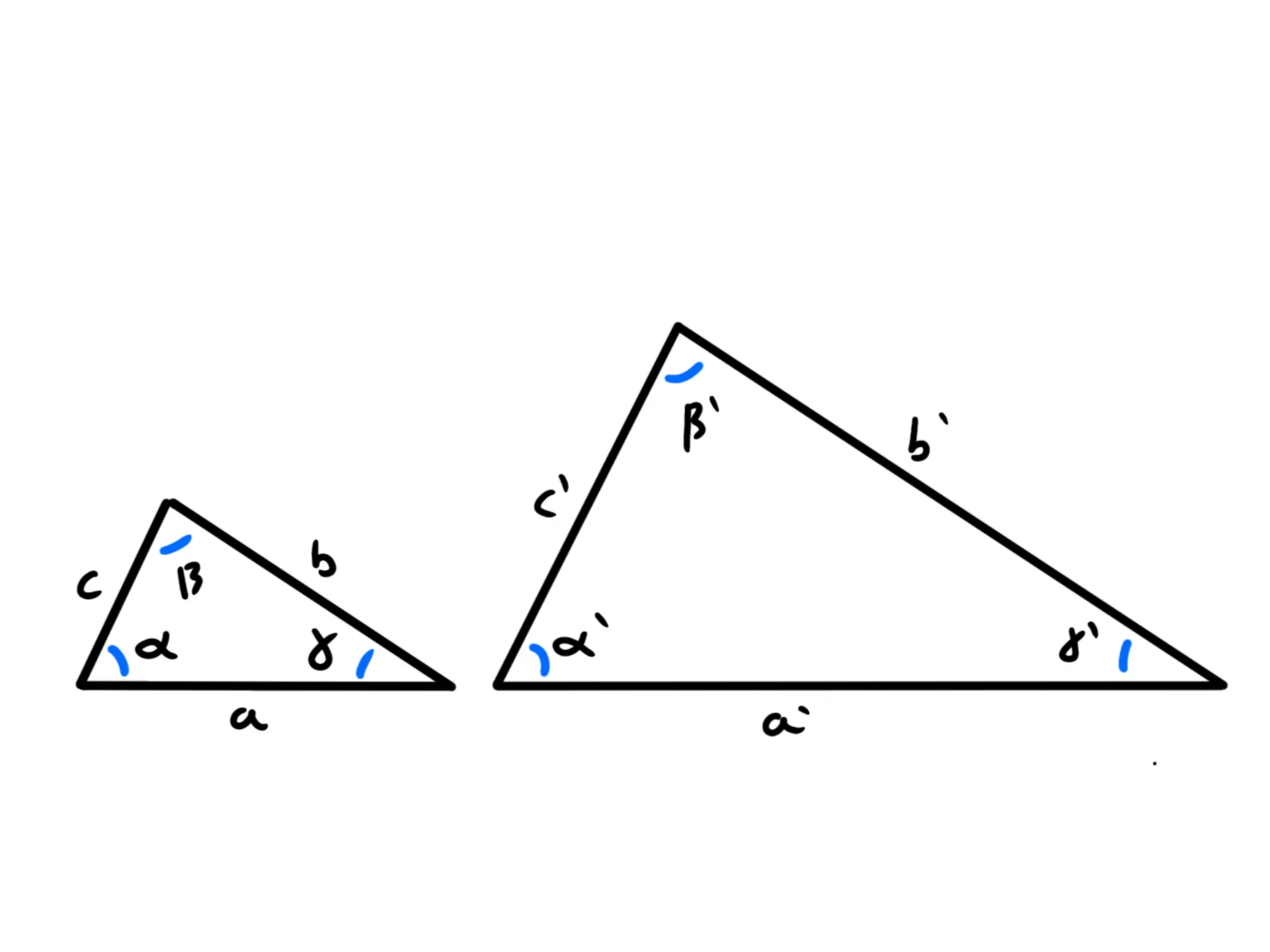
Nel grafico riportato sopra, dovremo avere $\displaystyle { \alpha = \alpha ', \beta = \beta ' }$ e $\displaystyle { \gamma = \gamma '. }$ Inoltre, tutti i rapporti tra i rispettivi lati devono essere uguali:

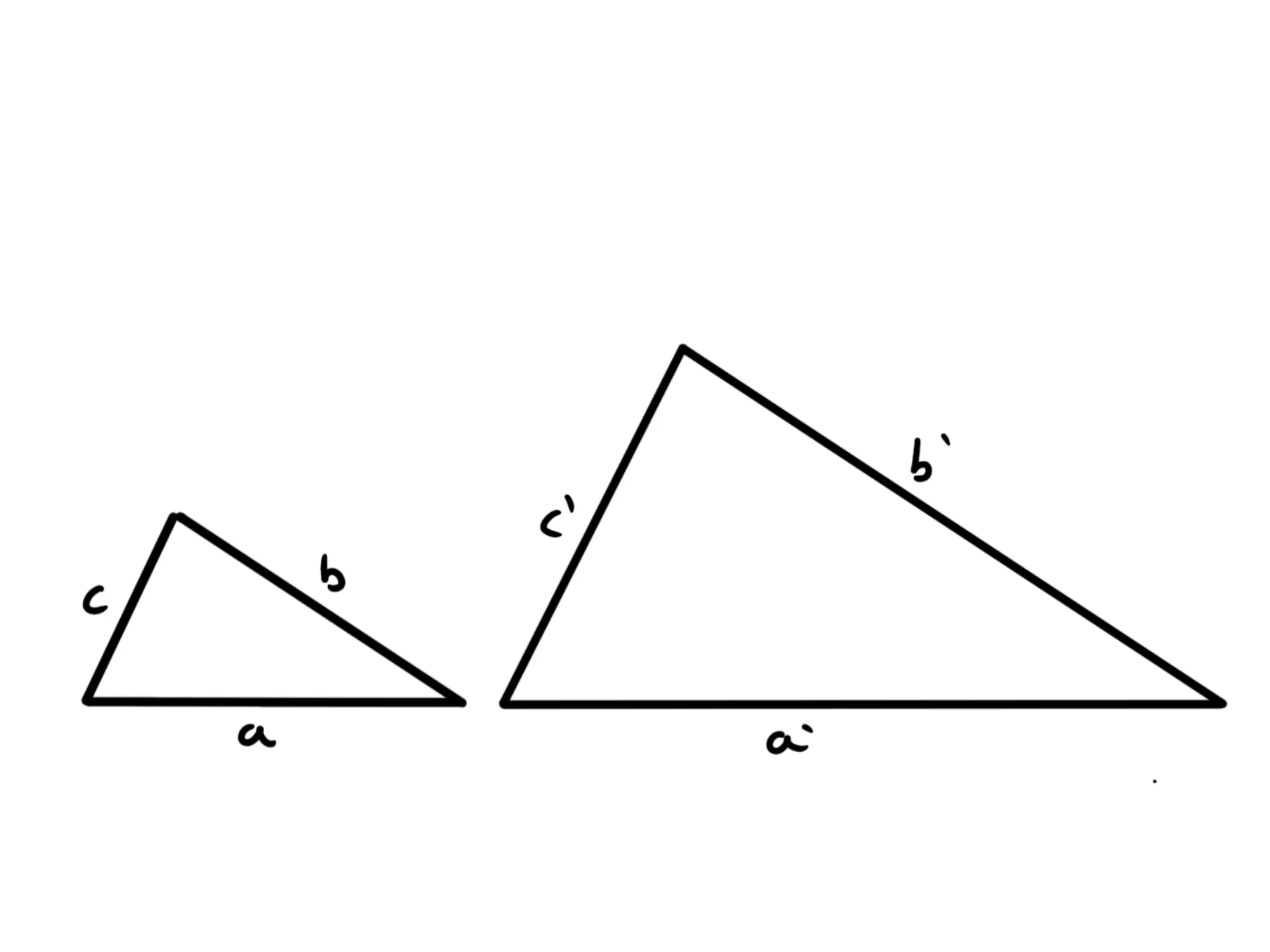
Nel grafico sopra, dobbiamo avere:

$\displaystyle { {a\over a'} = {b\over b'} = {c\over c'} }$

Appare logico, infatti, che se abbiamo ridotto in scala un triangolo, i rapporti fra tutti i suoi lati devono essere uguali perché abbiamo rimpicciolito o ingrandito ognuno di loro nello stesso modo.

Esistono tre criteri per determinare se due triangoli sono simili:

Criteri di similitudine

Il primo criterio di similitudine afferma che:

Se due triangoli hanno due angoli congruenti, allora sono simili.

Questo perché la somma degli angoli interni di un triangolo è sempre $\displaystyle { 180^{\circ}, }$ quindi anche il terzo deve essere uguale perché la somma di tutti e tre deve essere la stessa.

Il secondo criterio di similitudine afferma che:

Se due triangoli hanno due lati proporzionali e gli angoli compresi
tra loro sono congruenti, allora questi due triangoli sono simili.

Questo perché siccome l'angolo è uguale, si può dimostrare che anche i terzi lati sono proporzionali, dunque i triangoli sono simili.

Il terzo criterio di similitudine afferma che:

Come abbiamo anticipato prima, se due triangoli hanno tutti e tre i lati in proporzione, allora sono
due triangoli simili.