Momento delle forze

Cos'è il momento di una forza

Se stiamo facendo ruotare un oggetto, ci sarà almeno un punto fermo intorno a cui esso ruota. Per esempio, se stiamo facendo girare un disco, il suo centro sta fermo. Se stiamo aprendo una porta, il punto di contatto con i cardini sta fermo. Se stiamo facendo girare una palla, il suo centro sta fermo, e così via.

Chiamiamo questo punto fermo fulcro .

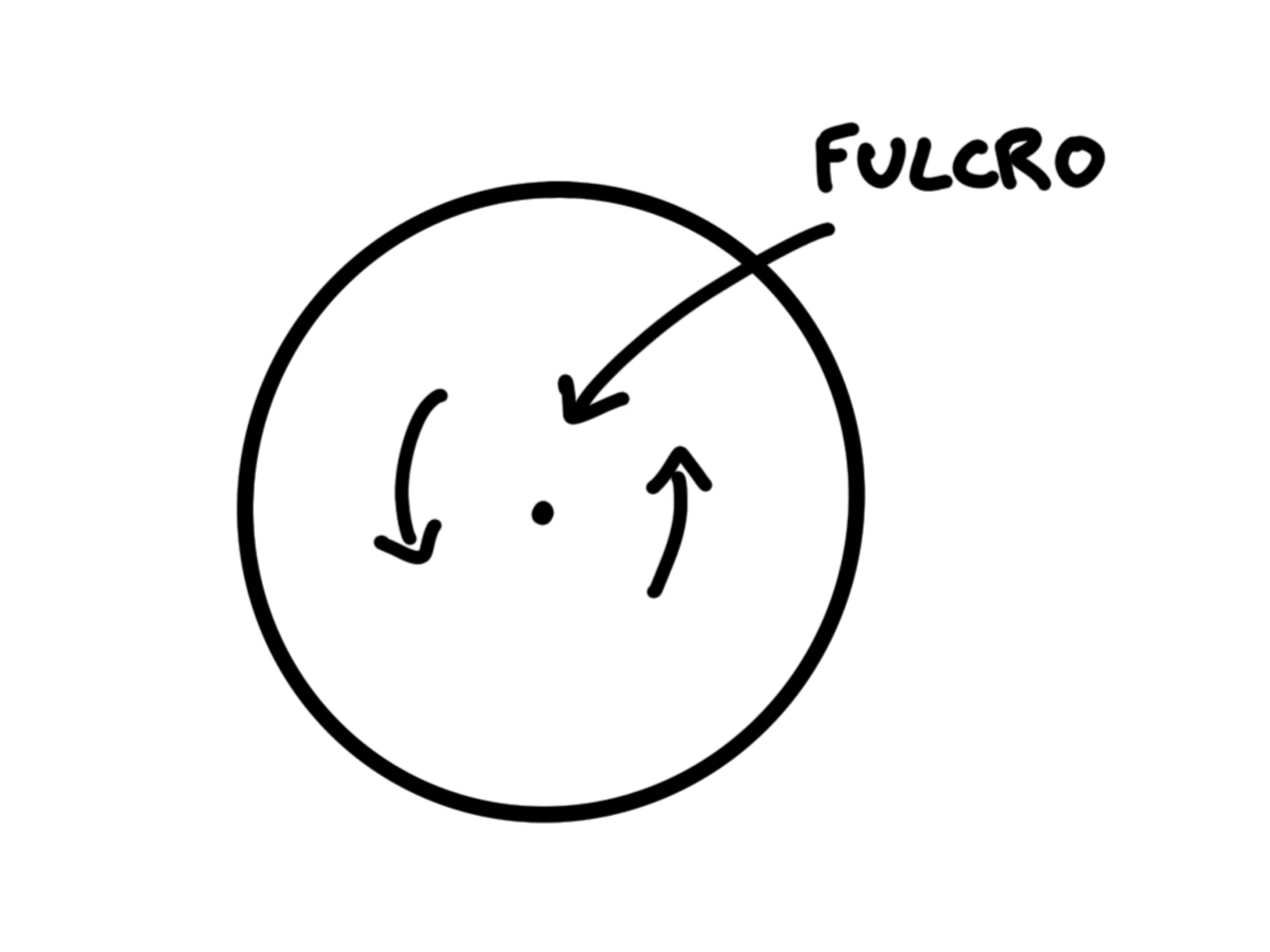
Per farlo girare, potremmo star spingendo un punto all'estremità del disco. In termini fisici, spingerlo significa applicargli una forza $\displaystyle { \overrightarrow{F} }$

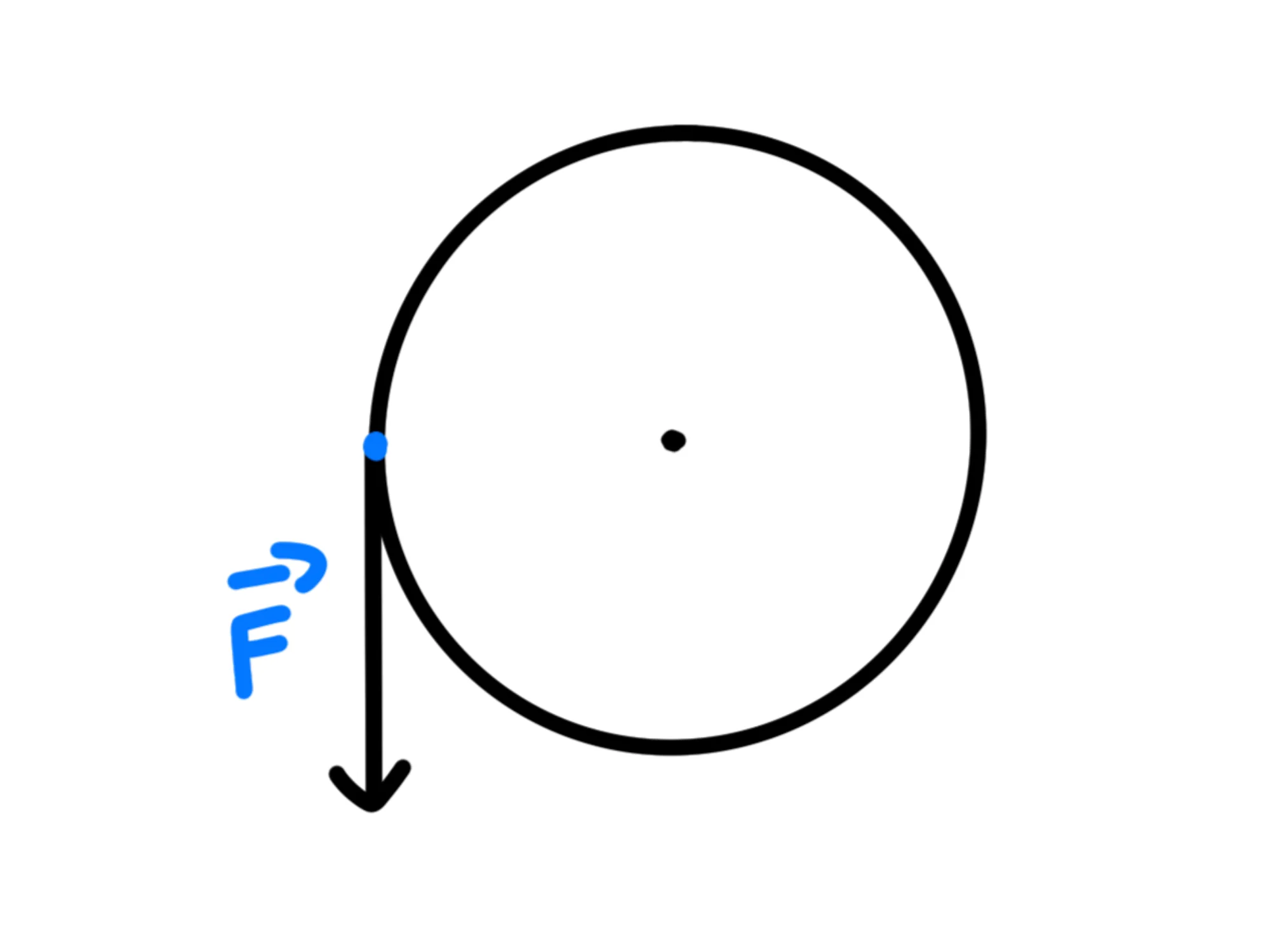
Adesso chiamiamo braccio della forza il vettore $\displaystyle { \overrightarrow{b} }$ che congiunge il fulcro al punto in cui viene applicata la forza:

Infine, chiamiamo $\displaystyle { \theta }$ l'angolo che si forma tra la forza e il suo braccio (nel nostro disegno $\displaystyle { \theta }$ vale $\displaystyle { 90^\circ }$ ):

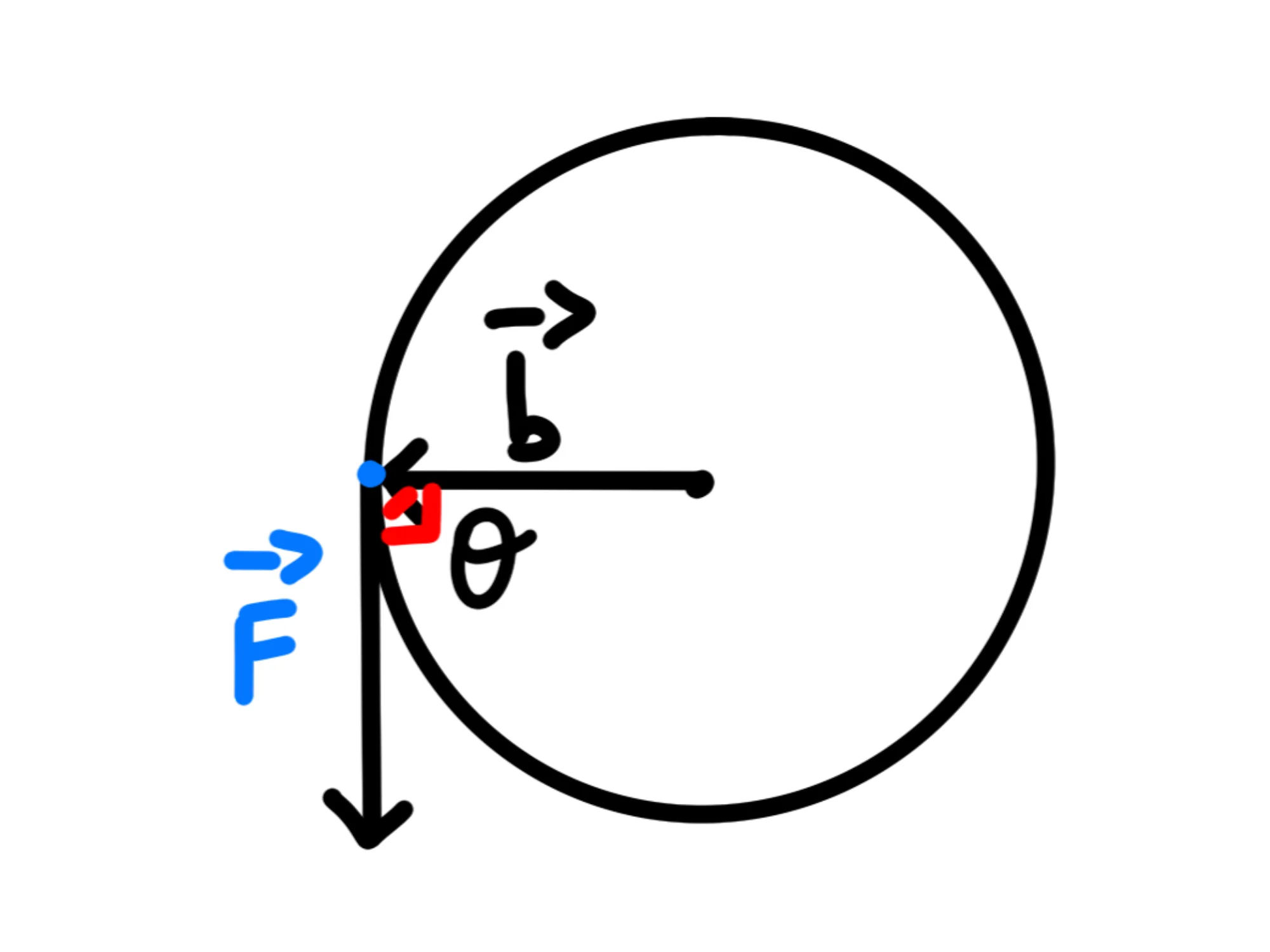
Adesso siamo finalmente pronti per definire il momento della forza :

Il momento $\displaystyle { \overrightarrow{M} }$ della forza $\displaystyle { \overrightarrow{F} }$ è definito come il prodotto vettoriale tra il braccio $\displaystyle { \overrightarrow{b} }$ e la forza $\displaystyle { \overrightarrow{F}: }$$\displaystyle { \overrightarrow{F}: }$

$\displaystyle { \overrightarrow{M} = \overrightarrow{b}\times \overrightarrow{F} }$

Che cos'è il prodotto vettoriale? Per studiarlo più approfonditamente vi rimandiamo alla nostra lezione dedicata interamente ai vettori (clicca qui), sennò rimanete qui per ripassarlo velocemente:

Iniziamo notando che il risultato di un prodotto vettoriale è un vettore, per questo il momento di una forza è un vettore e dunque avrà un modulo, una direzione ed un verso.

Per il modulo è semplice, basta moltiplicare il modulo dei due fattori per il seno dell'angolo tra i due. Nel nostro caso dunque avremo:

$\displaystyle { M = bF\sin(\theta) }$

La sua direzione è la retta perpendicolare sia a $\displaystyle { \overrightarrow{b} }$ che a $\displaystyle { \overrightarrow{F}, }$ quindi starà o entrando o uscendo dal vostro foglio (o dalla lavagna):

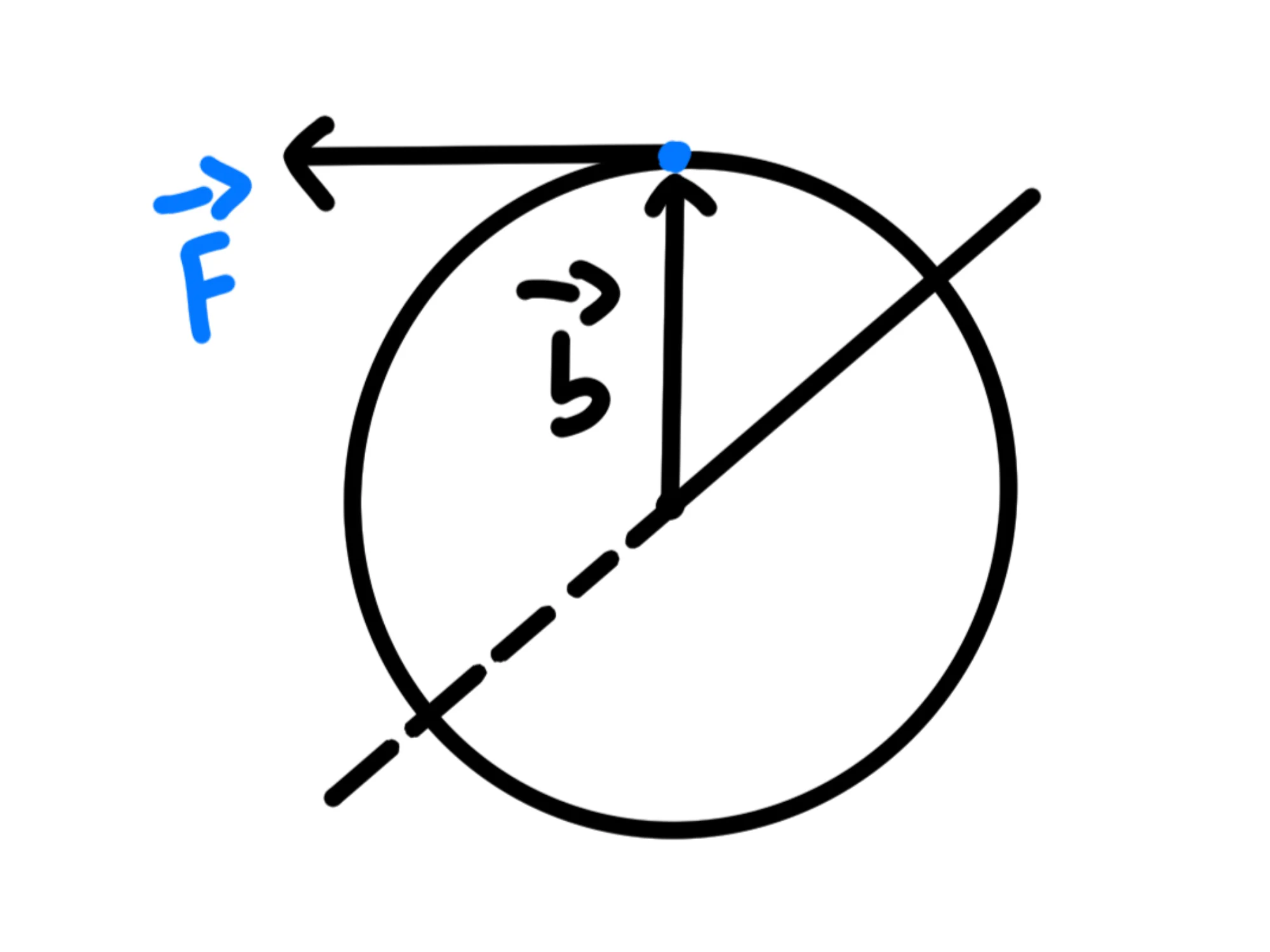
Adesso dobbiamo solo trovare il suo verso. Per farlo, dobbiamo usare la regola della mano destra:

Trasliamo i vettori affinchè le loro code coincidano:

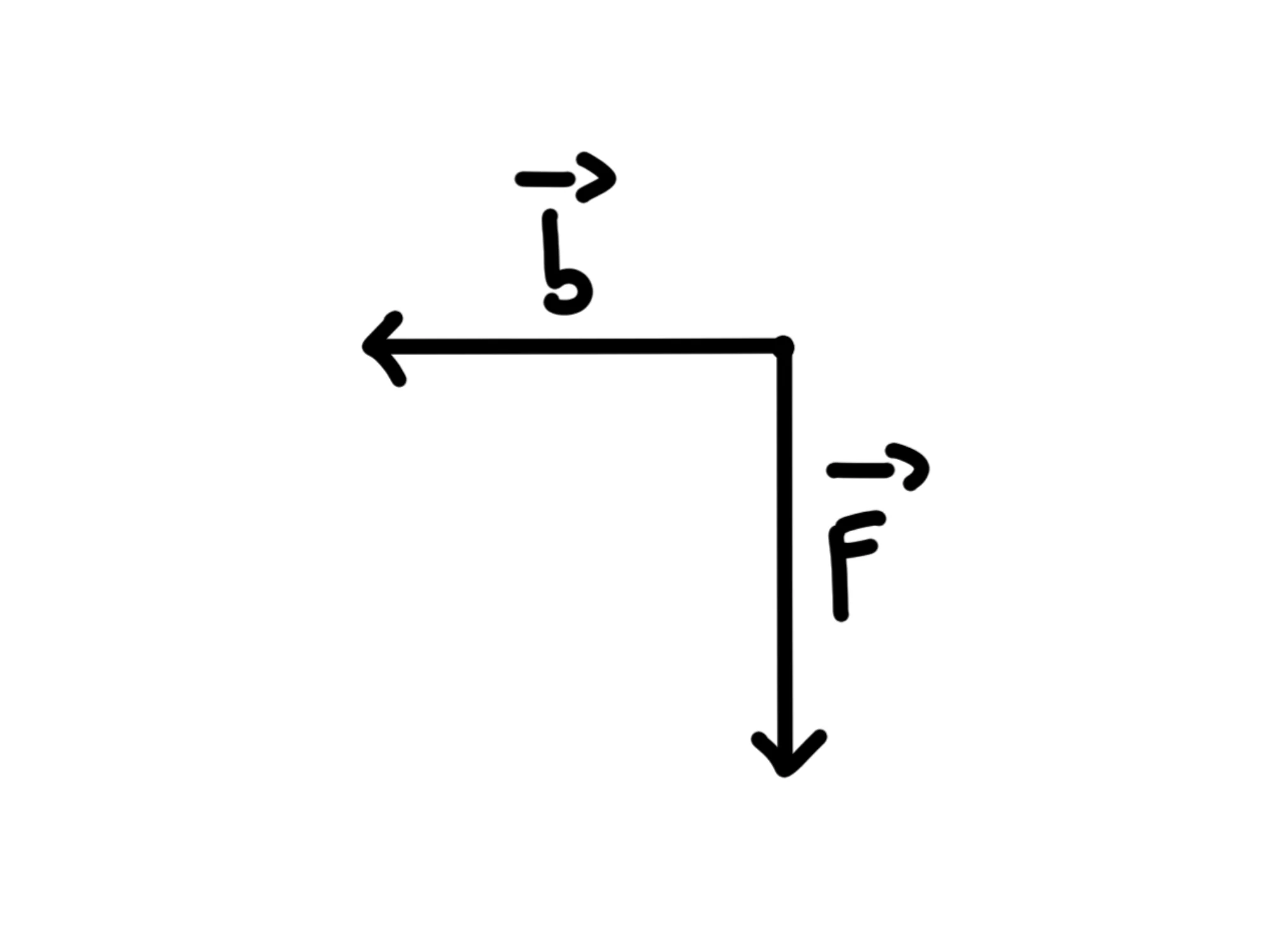
Adesso dobbiamo cercare di far ruotare il primo vettore (nel nostro caso $\displaystyle { \overrightarrow{b} }$ ) sul secondo (nel nostro caso $\displaystyle { \overrightarrow{F} }$ ) usando la mano destra:

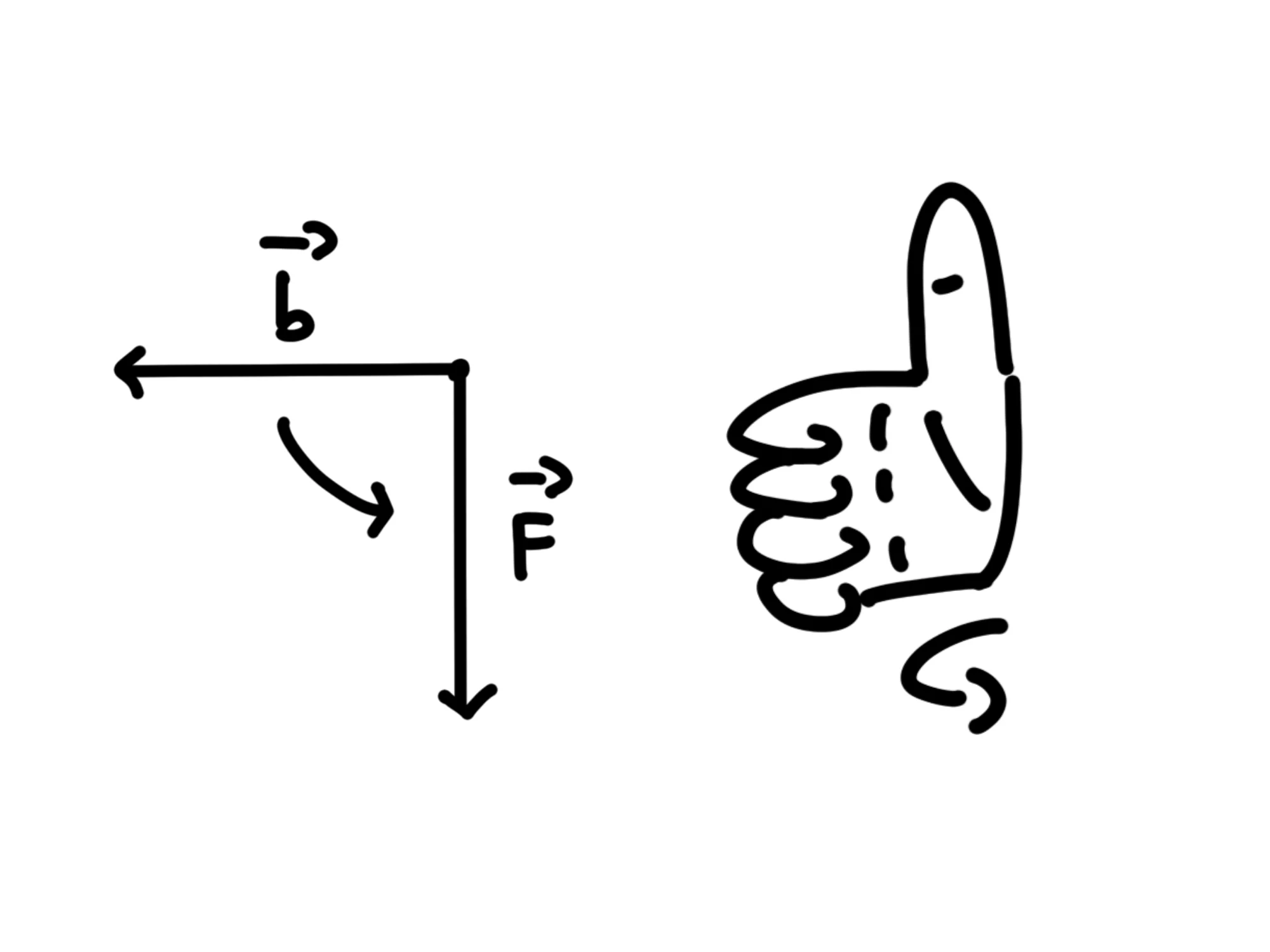
Quindi basterà guardare dove punta il vostro pollice: quello sarà il verso del momento della forza.

Nel nostro esempio il vostro pollice punterà verso fuori allo schermo.

Se invece di fare $\displaystyle { \overrightarrow{b}\times\overrightarrow{F} }$ facciamo $\displaystyle { \overrightarrow{F}\times\overrightarrow{b}, }$ dovremo muovere $\displaystyle { \overrightarrow{F} }$ su $\displaystyle { \overrightarrow{b} }$ e facendolo, nel nostro esempio, noterete che il vostro pollice starà puntando verso lo schermo.

Quindi gli abbiamo cambiato il verso, il che è uguale a moltiplicare per $\displaystyle { -1. }$ Per questo, il prodotto vettoriale non è commutativo e vale la seguente relazione:

$\displaystyle { \overrightarrow{b}\times\overrightarrow{F} = -\overrightarrow{F}\times\overrightarrow{b} }$

Per convenzione, il momento della forza ha, solitamente, segno positivo quando ha verso uscente dal foglio, mentre ha segno negativo quando ha verso entrante nel foglio.

Più forze

Come calcolare il momento totale nel caso in cui ci siano più forze?

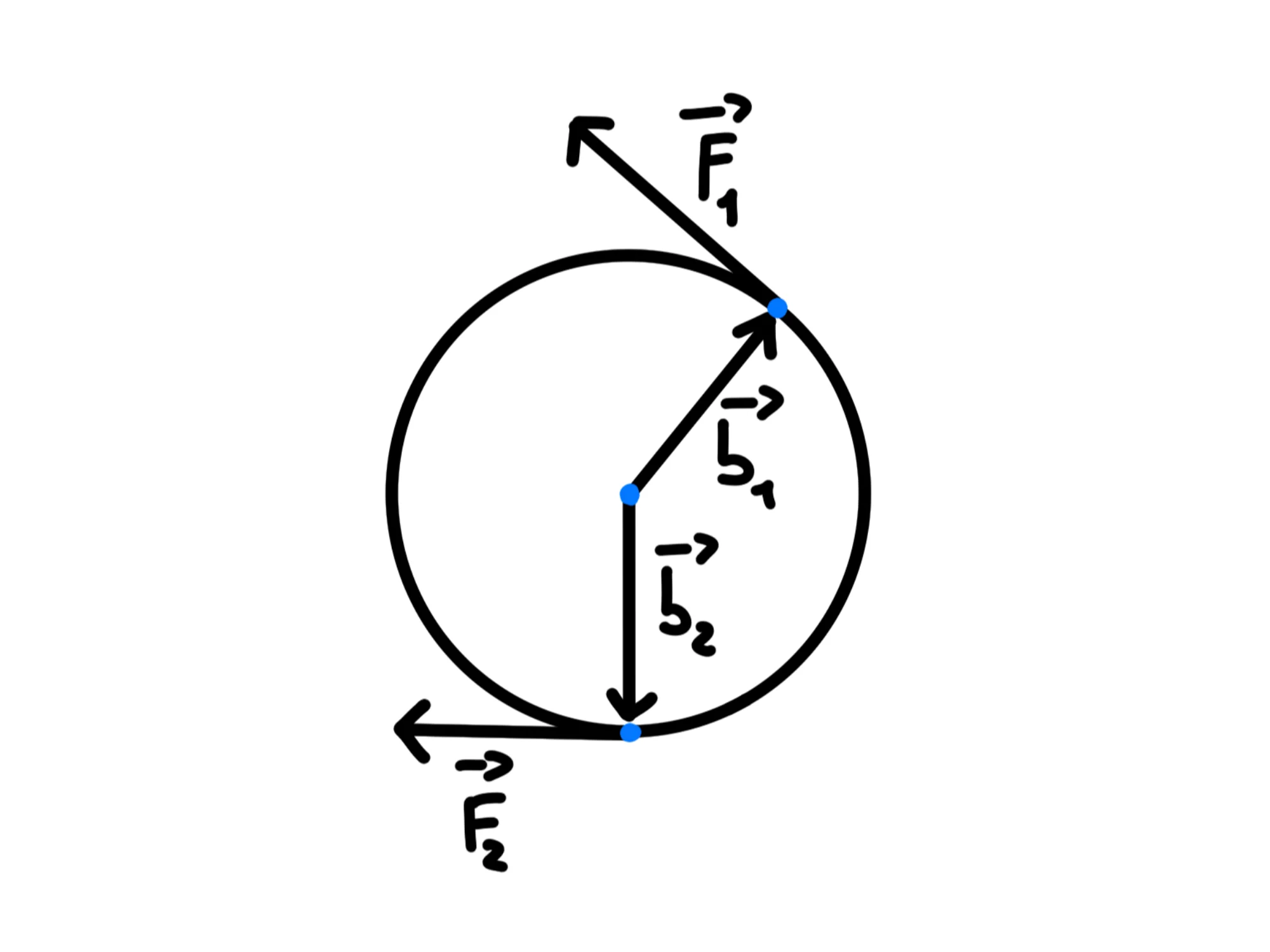
Per calcolare il momento totale, dovremo prima calcolare i momenti delle singole forze e solo dopo sommarli:

Nel disegno sopra riportato, dunque, avremo:

$\displaystyle { \overrightarrow{M_1} = \overrightarrow{b_1}\times \overrightarrow{F_1} }$

$\displaystyle { \overrightarrow{M_2} = \overrightarrow{b_2}\times \overrightarrow{F_2} }$

$\displaystyle { \overrightarrow{M_\text{tot}}= \overrightarrow{M_1}+\overrightarrow{M_2} }$

Il momento delle forze ha molte applicazioni in fisica. Per esempio, è fondamentale quando vogliamo determinare se un corpo rigido si trova in equilibrio o meno.