Disequazioni esponenziali
Di seguito analizzeremo tutte le tipologie di disequazioni esponenziali che potete incontrare e vedremo come risolverle.
Cosa devo già sapere?
Cos'è una disequazione esponenziale?
Una disequazione esponenziale è una disequazione in cui appare almeno una potenza con un'incognita nell'esponente. Esse sono quindi disequazioni del tipo:
a^{f(x)} > g(x)
o con < ,\geq o \leq al posto di >.
Può sembrare molto complicato, ma tranquilli, vedremo solo i casi particolari che incontrerete a scuola.
Partiamo da quello più semplice in assoluto, dove f(x) = x e g(x) è costante. Avremo quindi disequazioni del tipo:
a^x > b
Dobbiamo dividere queste disequazioni in due casi:
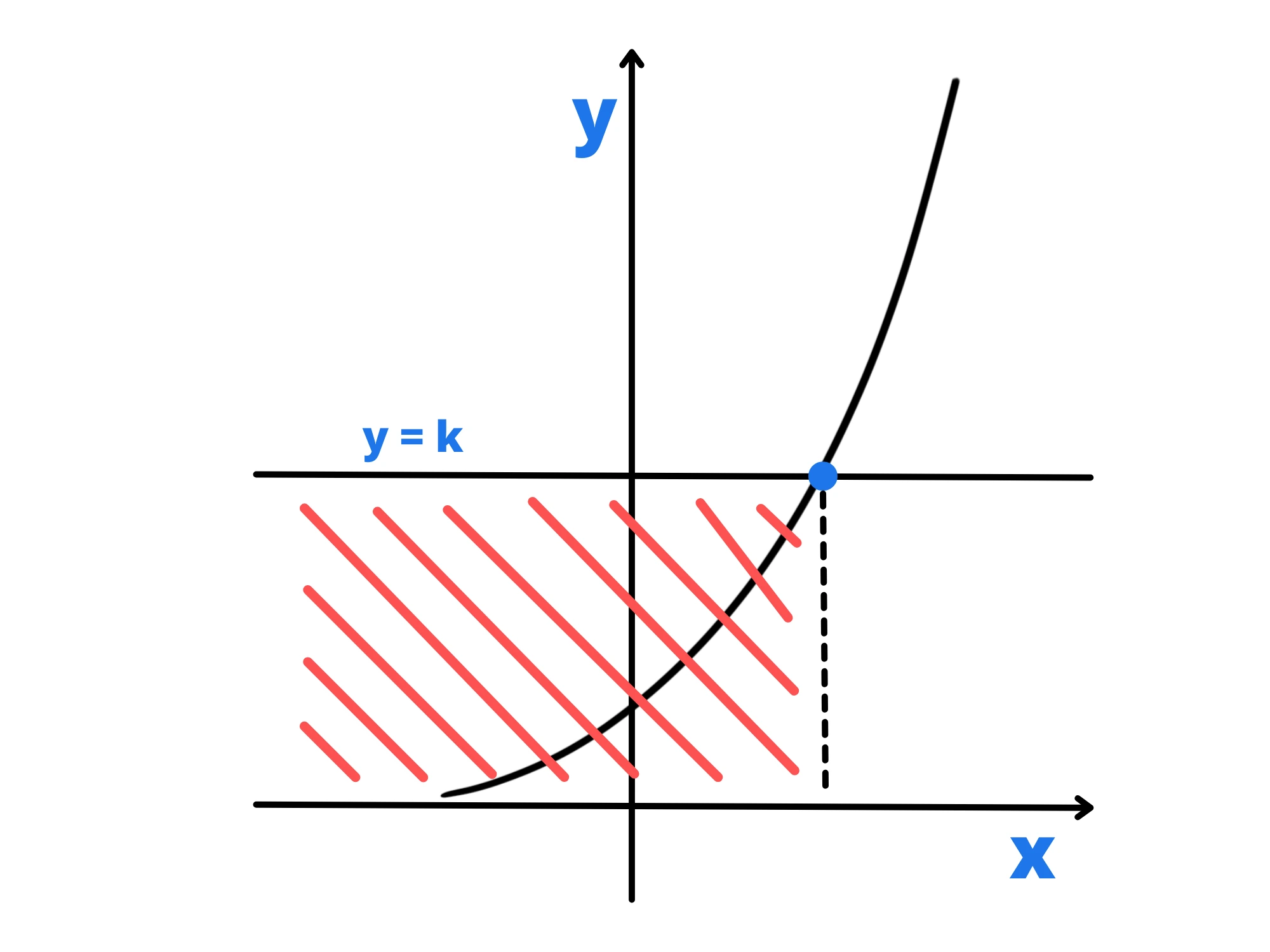
La base a è maggiore di 1
In questo caso per prima cosa risolviamo l'equazione associata:
a^x =b
Una volta fatto questo, sapendo che la funzione a^x è monotona crescente (ovvero aumenta sempre), troviamo la soluzione della disequazione.
Vediamo qualche esempio.
Risolviamo la disequazione esponenziale:
3^x > 81
Risolviamo l'equazione associata:
3^x = 81
3^x = 3^4
x= 4
Sappiamo che 3^x aumenta sempre, quindi per x > 4 sarà sempre maggiore di 81. Quindi la soluzione è x>4.
Risolviamo la disequazione esponenziale:
5^x \leq 125
Risolviamo l'equazione associata:
5^x = 125
5^x = 5^3
x= 3
Sappiamo che 5^x aumenta sempre, quindi per x>3 sarà sempre maggiore di 125, mentre per x < 3 sarà sempre minore di 125. La soluzione è quindi x \leq 3.
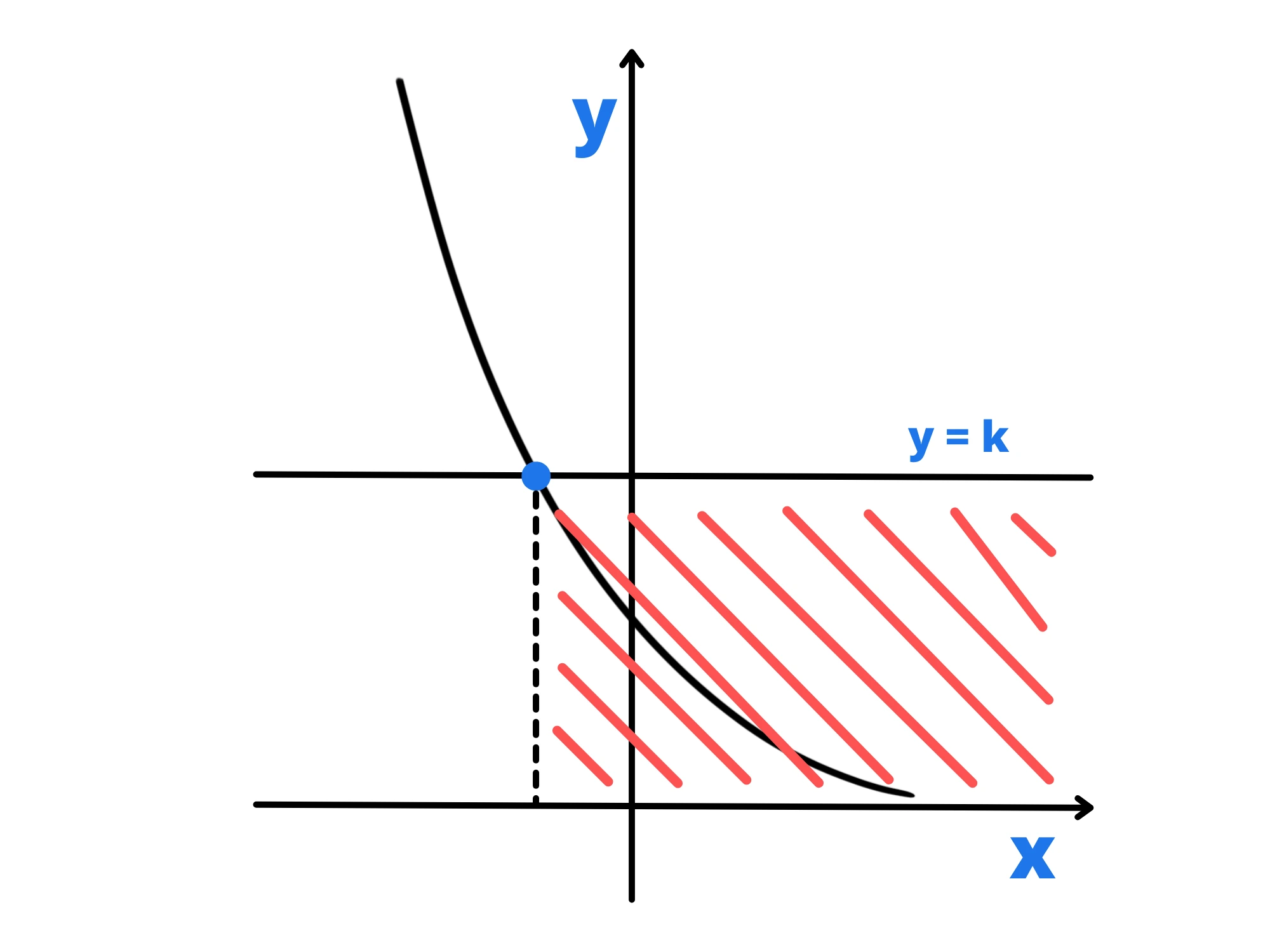
La base a è compresa tra 0 e 1
In tal caso il procedimento è lo stesso, ma questa volta la funzione sarà monotona decrescente (ovvero diminuisce sempre).
Vediamo qualche esempio:
Risolviamo la disequazione esponenziale:
({1 \over 2})^x < {1\over 32}
Risolviamo l'equazione associata:
({1\over 2})^x ={1\over 32}
({1\over 2})^x =({1\over 2})^5
x=5
Siccome ({1\over 2})^x diminuisce sempre, per x>5 sarà sempre minore di {1\over 32}, quindi la soluzione è proprio x>5.
Risolviamo la disequazione esponenziale:
({1\over 3})^x \geq {1\over 9}
Risolviamo l'equazione associata:
({1\over 3})^x ={1\over 9}
({1\over 3})^x =({1\over 3})^2
x=2
Siccome ({1\over 3})^x diminuisce sempre, per x>2 sarà sempre minore di {1\over 9} e sarà invece maggiore di {1\over 9} per x < 2, quindi la soluzione è proprio x\leq 2.
Disequazioni esponenziali risolvibili con i logaritmi
Usando i logaritmi possiamo risolvere disequazioni esponenziali più complicate, dove possono apparire più potenze con incognite all'esponente. Ci basterà applicare il logaritmo base 10 da entrambi i lati e semplificare. Possiamo pure applicare logaritmi con altre basi, ma se è compresa tra 0 ed 1 dobbiamo cambiare il segno della disequazione, perché:
Se abbiamo x>y, se a>1, avremo:
\log_{a} (x) >\log_{a} (y)
Mentre se 0 < a < 1 , avremo:
\log_{a} (x) < \log_{a} (y)
In generale conviene quindi applicare sempre il logaritmo base 10 e non avere paura di dover cambiare qualcosa.
Vediamo qualche esempio:
Risolviamo la disequazione esponenziale:
5\cdot 3^x > 2^{x-3}
Abbiamo quantità positive da entrambi i lati, quindi applichiamo il logaritmo base 10 da entrambi i lati:
\log_{10}(5 \cdot 3^x) > \log_{10}(2^{x-3})
Applichiamo la proprietà del logaritmo di un prodotto e sottintendiamo \log_{10} con \log:
\log (5) + \log (3^x) > \log (2^{x-3})
Applichiamo la proprietà del logaritmo di una potenza ed isoliamo x:
\log(5) + x \log(3) > (x-3) \log(2)
\log (5) + x\log (3) >x\log(2) -3\log(2)
x\log(3) - x\log(2) > -\log(5) -3\log(2)
x( \log(3) -\log(2))>-(\log(5)+3\log(2))
Siccome \log(3) -\log(2) è una quantità positiva, possiamo dividere entrambi i lati per essa:
x> -\frac{\log(5)+3\log(2)}{\log(3)-\log(2)}