Quando la luce, o in generale un'onda, incontra una superficie riflettente, viene riflessa:
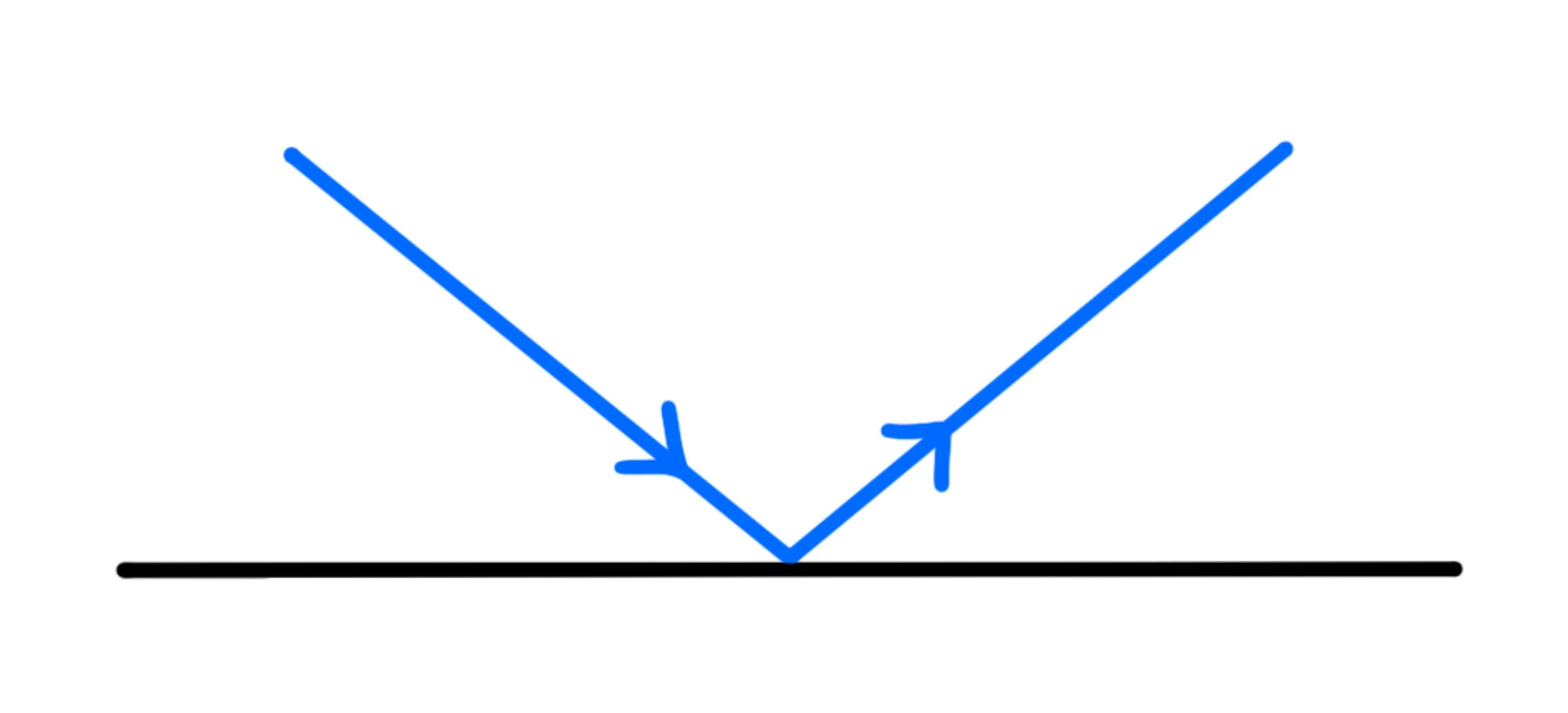
Per semplificare il disegno abbiamo rappresentato il raggio al posto dei fronti d'onda.
Ora dobbiamo introdurre un po' di nomenclatura:
Il raggio incidente è il raggio che arriva e che sbatte contro la superficie riflettente:
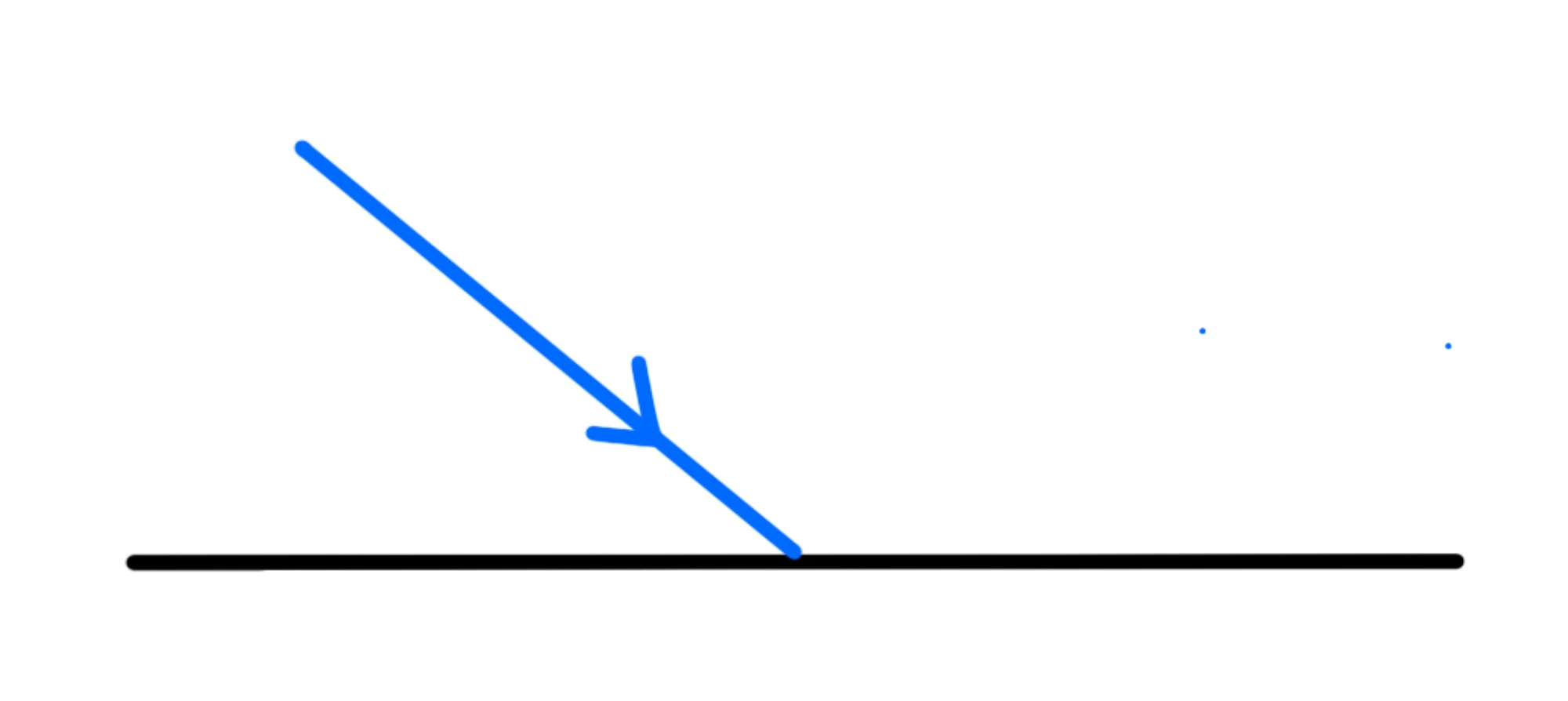
Il raggio riflesso è invece il raggio che se ne va via:
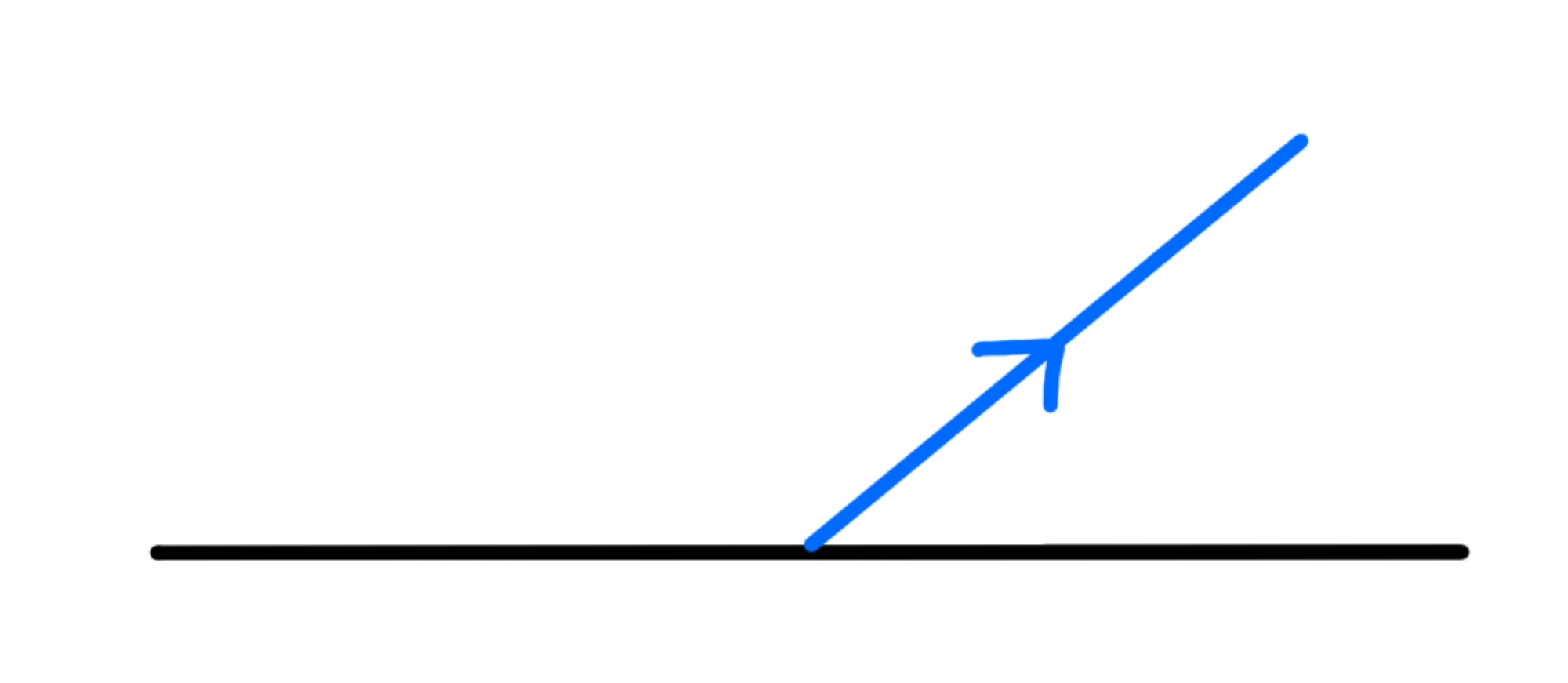
La normale al piano è una retta perpendicolare al piano su cui si riflette l'onda.
Può essere presa in qualsiasi punto, ma solitamente viene presa sul punto di incidenza, cioè il punto in cui il raggio incidente sbatte contro il piano:
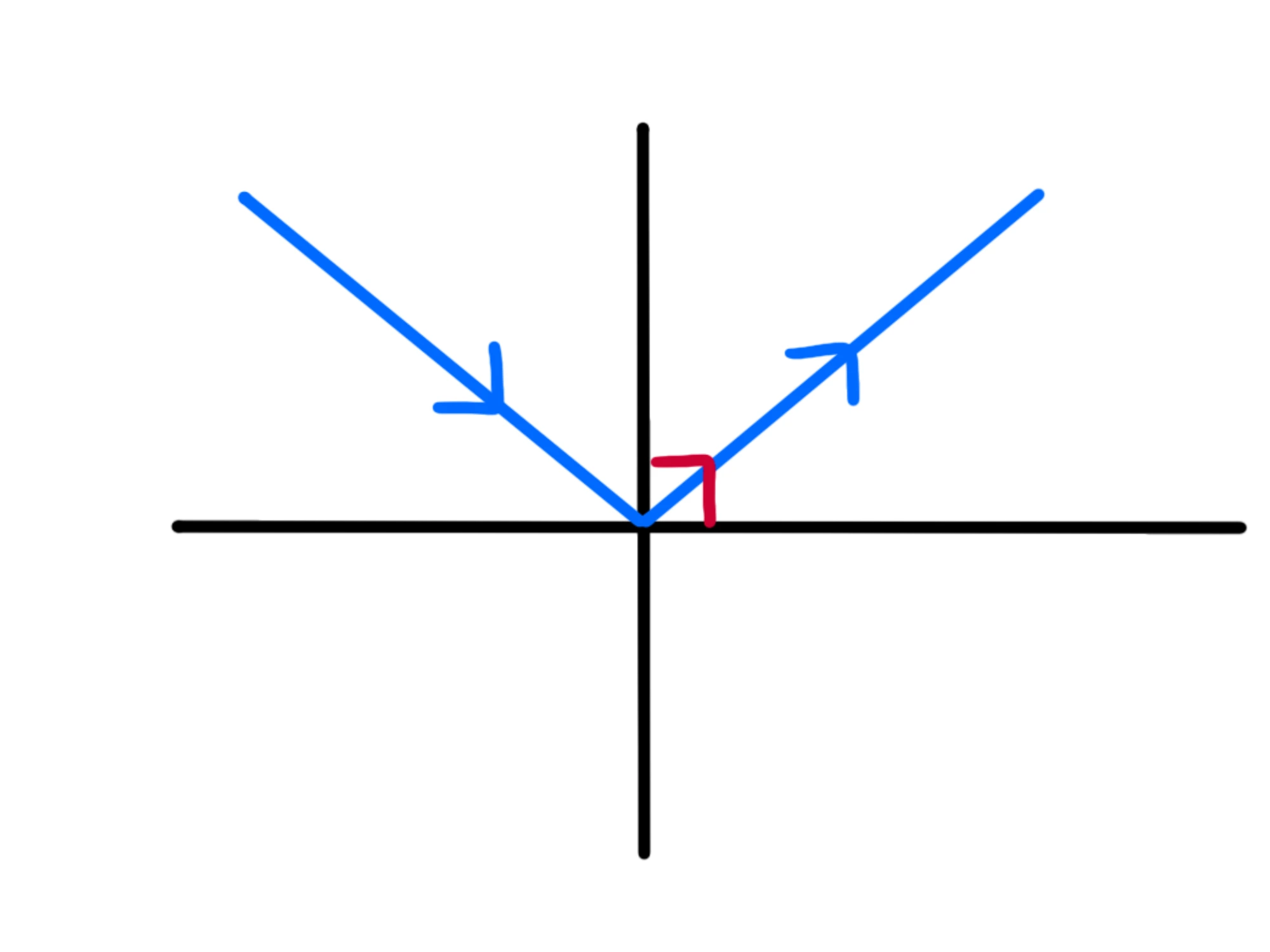
L'angolo di incidenza è l'angolo che il raggio incidente forma con la normale al piano e viene solitamente indicato con
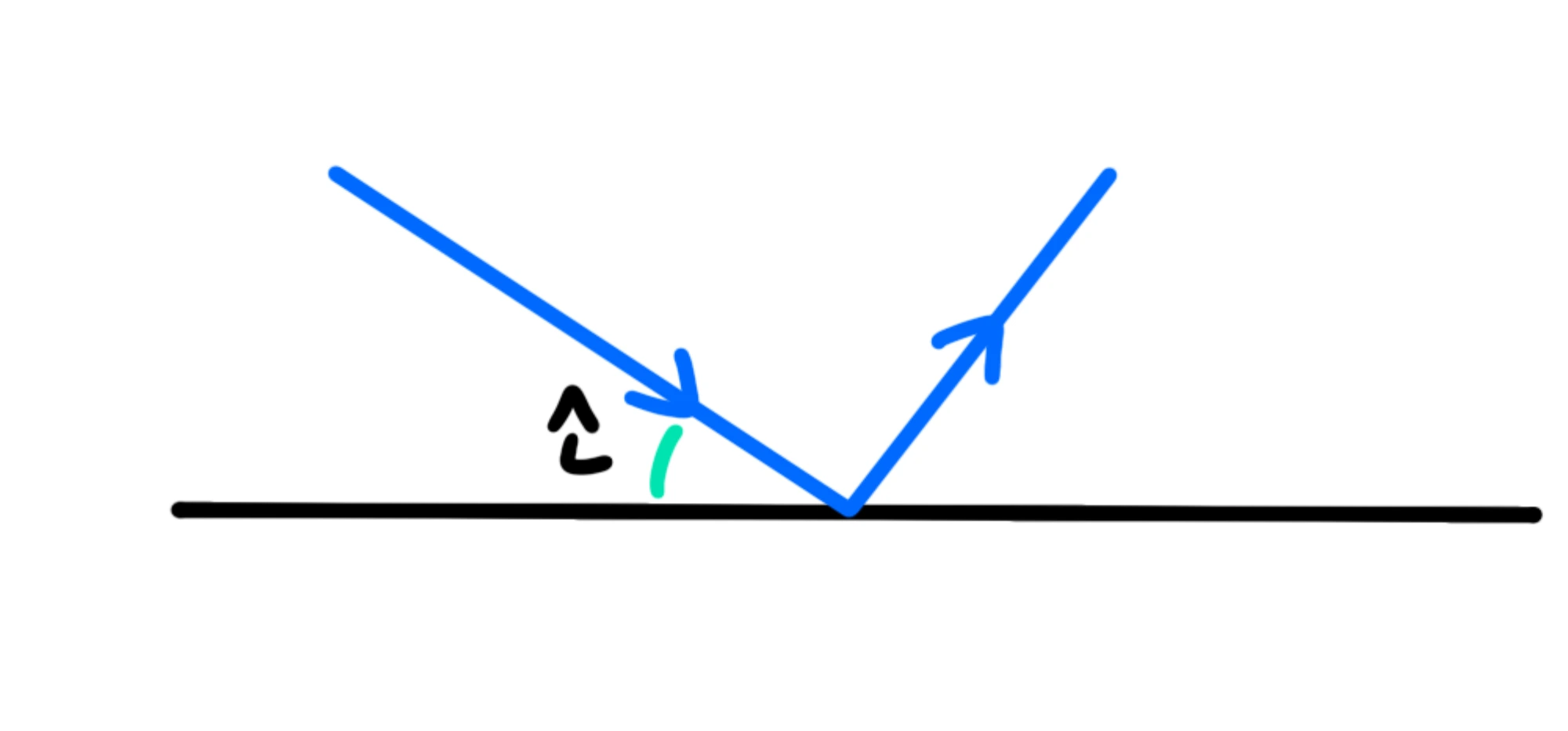
Infine, l'angolo di riflessione è l'angolo che il raggio riflesso forma con la normale al piano e viene solitamente indicato con
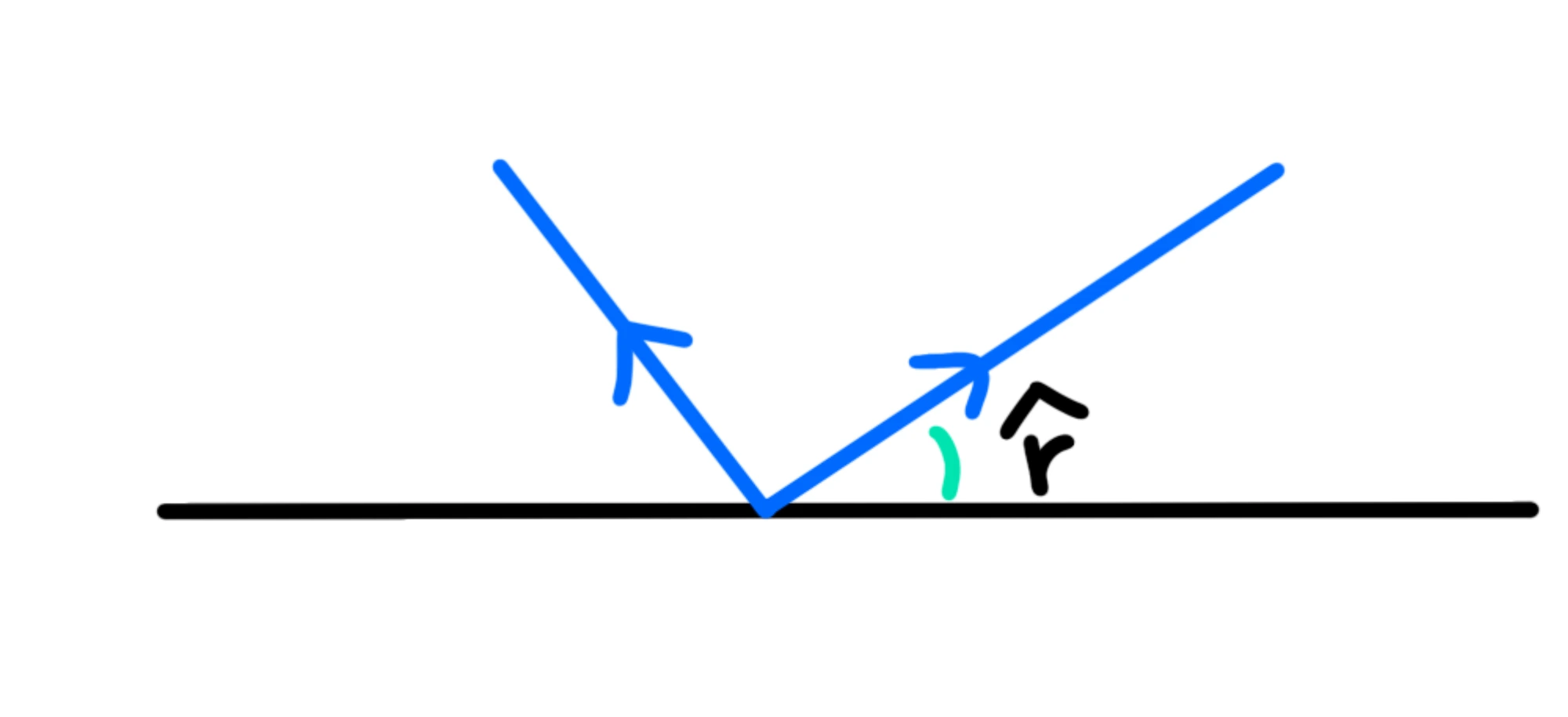
Ora che conosciamo per bene i nomi di tutti gli elementi, siamo pronti per studiare le due leggi della riflessione:
La prima legge della riflessione afferma che:
Il raggio incidente, quello riflesso e la normale al piano stanno tutti e tre nello stesso piano.
Può sembrare ovvia come cosa ma non è affatto scontata.
La seconda legge della riflessione afferma che:
L'angolo di incidenza è uguale all'angolo di riflessione $ \hat{r}. $
Questo ci dice che il raggio incidente e il raggio riflesso sono simmetrici rispetto alla normale al piano.
Per la riflessione non c'è molto altro da dire, quindi passiamo alla rifrazione:
Quando un'onda passa da un mezzo meno denso ad uno più denso, essa cambia direzione.
Lo si può vedere mettendo una cannuccia dentro un bicchiere d'acqua di vetro. Ci sembrerà che la cannuccia si sia spezzata a metà, ma in realtà è solo colpa della rifrazione.
Quindi, se la luce passa dall'aria a l'acqua succederà questo:
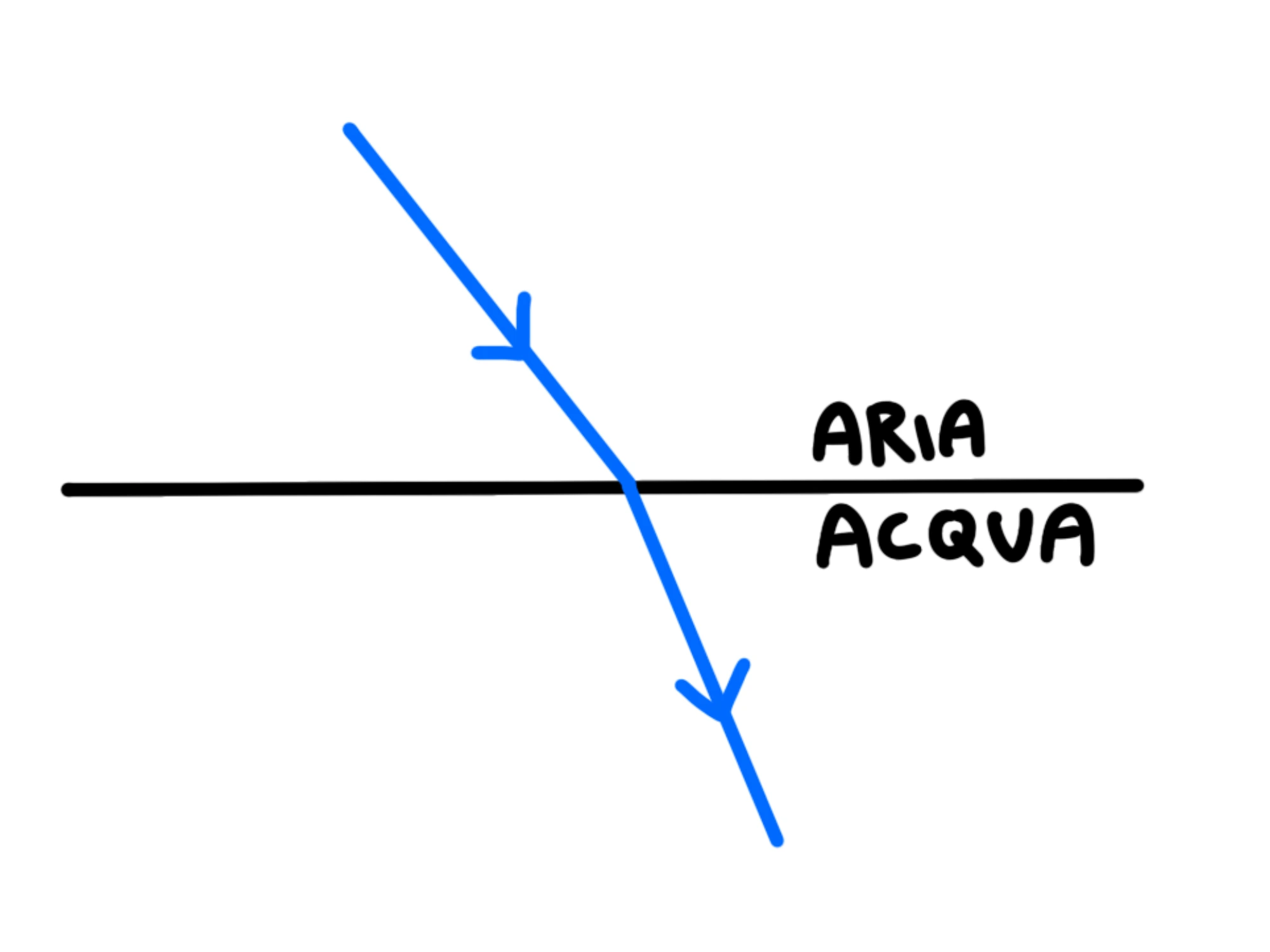
Anche in questo caso il raggio che arriva viene chiamato raggio incidente, la retta perpendicolare al piano è detta la normale al piano e l'angolo che si forma tra i due viene sempre chiamato angolo di incidenza.
Questa volta, però, invece di avere un raggio riflesso avremo un raggio rifratto:
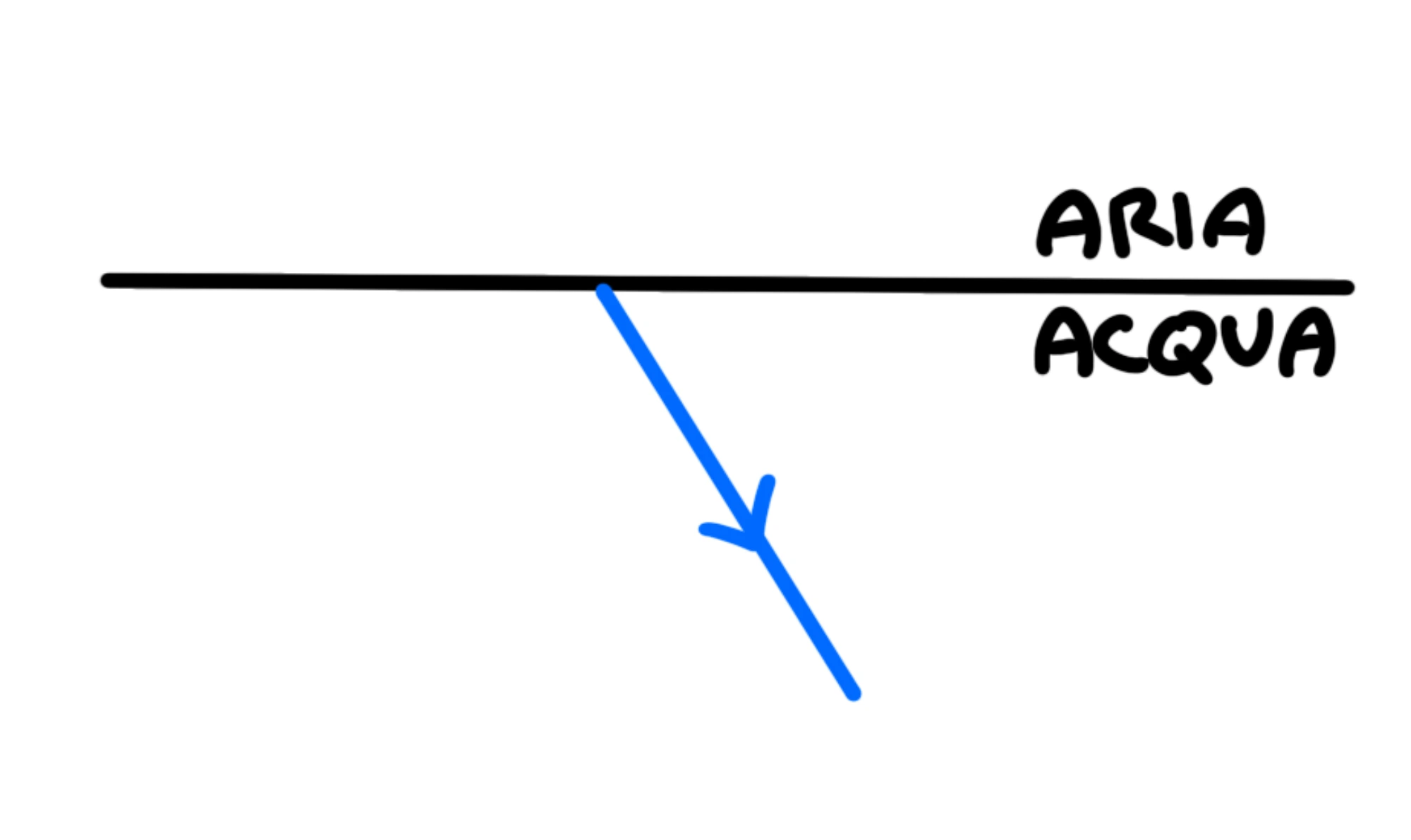
E l'angolo che esso forma con la normale al piano è detto angolo di rifrazione:
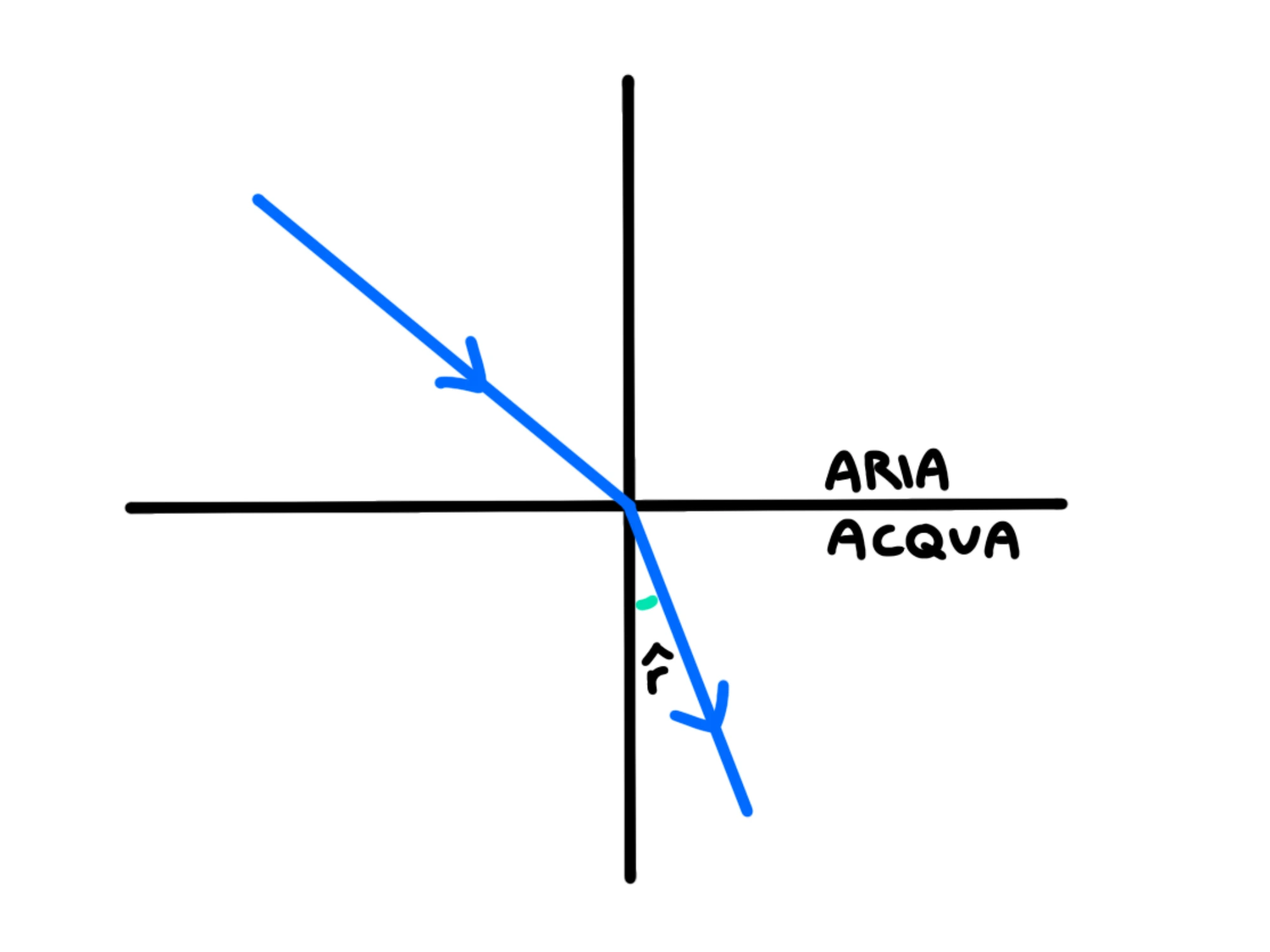
Viene anch'esso solitamente indicato come
La prima legge della rifrazione è molto simile a quella della riflessione. Essa infatti afferma che:
Il raggio incidente, quello rifratto e la normale al piano giacciono tutti sullo stesso piano.
Prima di passare alla seconda legge, dobbiamo prima introdurre qualche altro concetto:
Sappiamo bene che la velocità della luce nel vuoto vale all'incirca m/s e che si indica con la lettera
Quando la luce non si trova nel vuoto ma in un altro mezzo, come l'aria o l'acqua, essa rallenta.
Ogni mezzo, dunque, possiede un proprio indice di rifrazione che viene definito come il rapporto tra la velocità della luce nel vuoto e la velocità della luce in quel mezzo:
Siccome abbiamo detto che la luce rallenta, è sempre minore di e quindi è sempre maggiore di (o uguale ad se siamo nel vuoto).
Non è una coincidenza che si chiami indice di rifrazione. Esso ci permette, infatti, di conoscere la relazione tra l'angolo di incidenza e quello di rifrazione:
La seconda legge della rifrazione, o legge di Snell, ci dice infatti che la seguente relazione è sempre valida:
Dove è l'indice di rifrazione del primo mezzo e è quello del secondo.
Spesso viene scritta in quest'altra sua forma:
Siccome più un mezzo è denso e più il suo indice di rifrazione è alto, se la luce passa da un mezzo meno denso ad uno più denso (come dall'aria all'acqua), dovremo avere da cui si ottiene cioè l'angolo è più piccolo e quindi il raggio rifratto si avvicina alla normale.
Se invece si passa da un mezzo più denso ad uno meno denso (come dall'acqua all'aria), dovremo avere da cui otteniamo cioè che aumenta. Quindi il raggio rifratto si allontana dalla normale al piano:
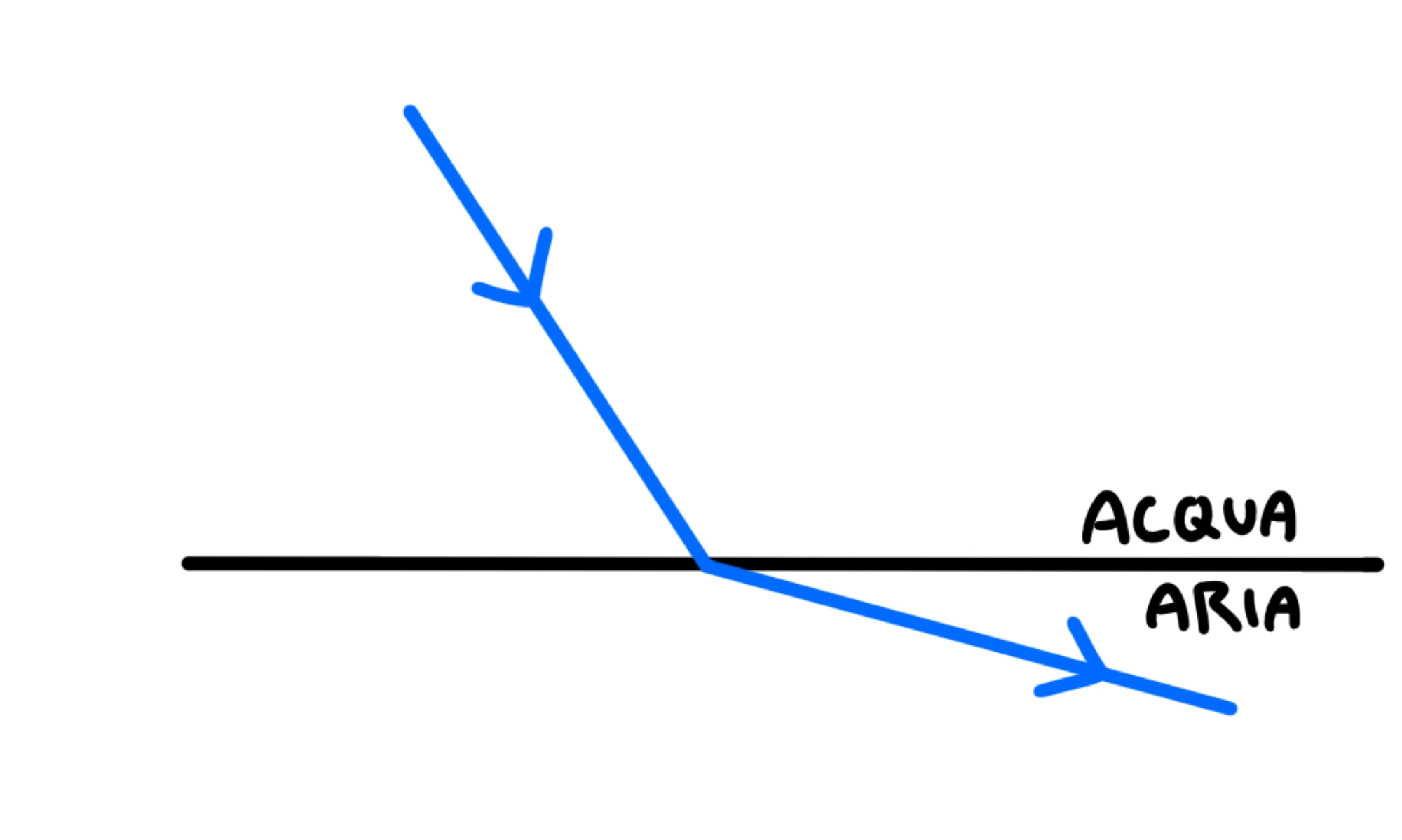
Cosa succede, quindi, se aumento talmente tanto da rendere un angolo di Otterremo che il raggio rifratto rimane tra il confine dei due mezzi:
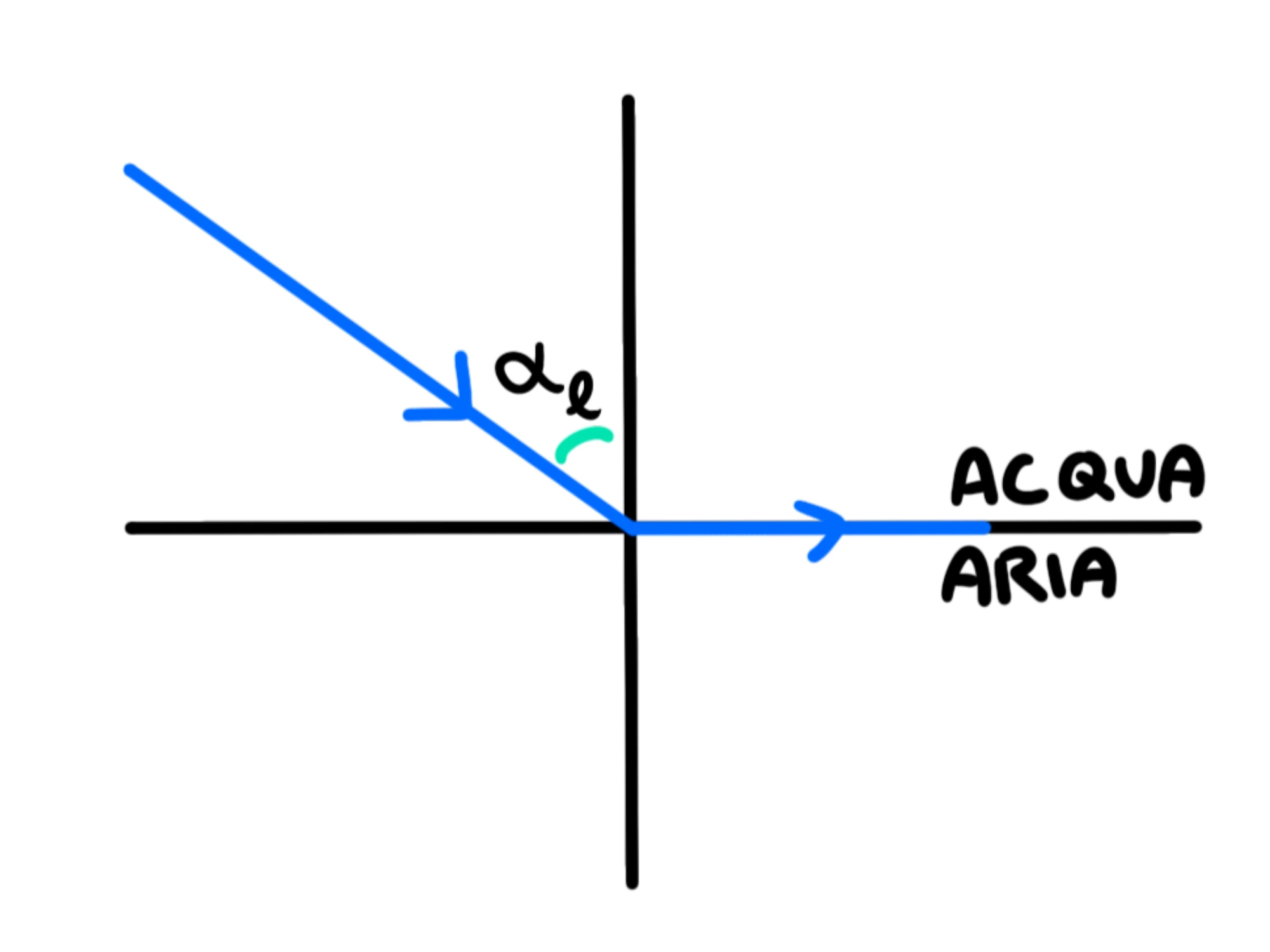
Come calcolare l'angolo limite che deve assumere affinché avvenga questo? Possiamo calcolarlo con la legge di Snell:
Se vale il suo seno vale quindi la formula si semplifica in:
Da qui possiamo trovare
Notate che non c'è bisogno di aggiungere le altre soluzioni dell'equazione goniometrica perché tanto deve essere compreso tra e
Nel caso dell'acqua-aria, si ottiene che l'angolo limite vale circa
Cosa succede se aumentiamo ancora di più Allora, per la legge di Snell, anche dovrà aumentare, quindi il raggio tornerà indietro nell'acqua:
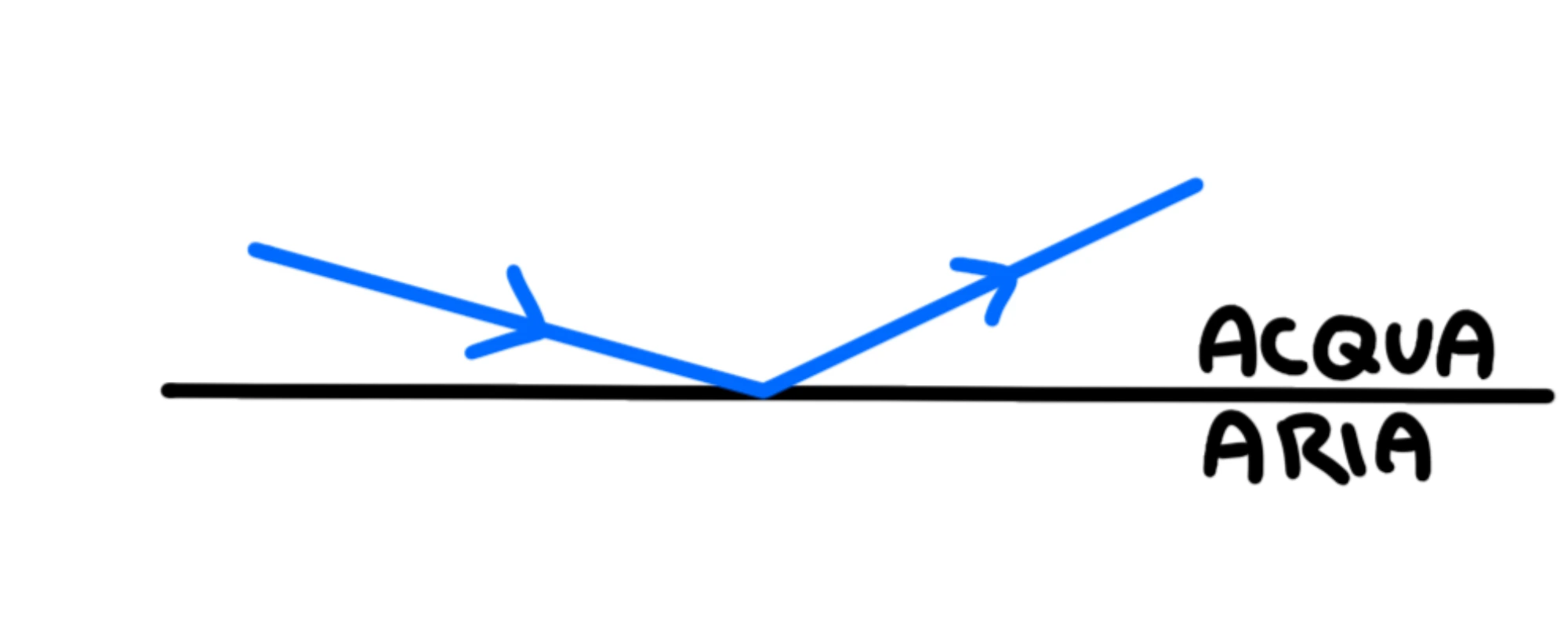
Dobbiamo notare, adesso, che indipendentemente dall'angolo di incidenza in realtà non tutta la luce viene rifratta, ma un po' viene sempre riflessa:
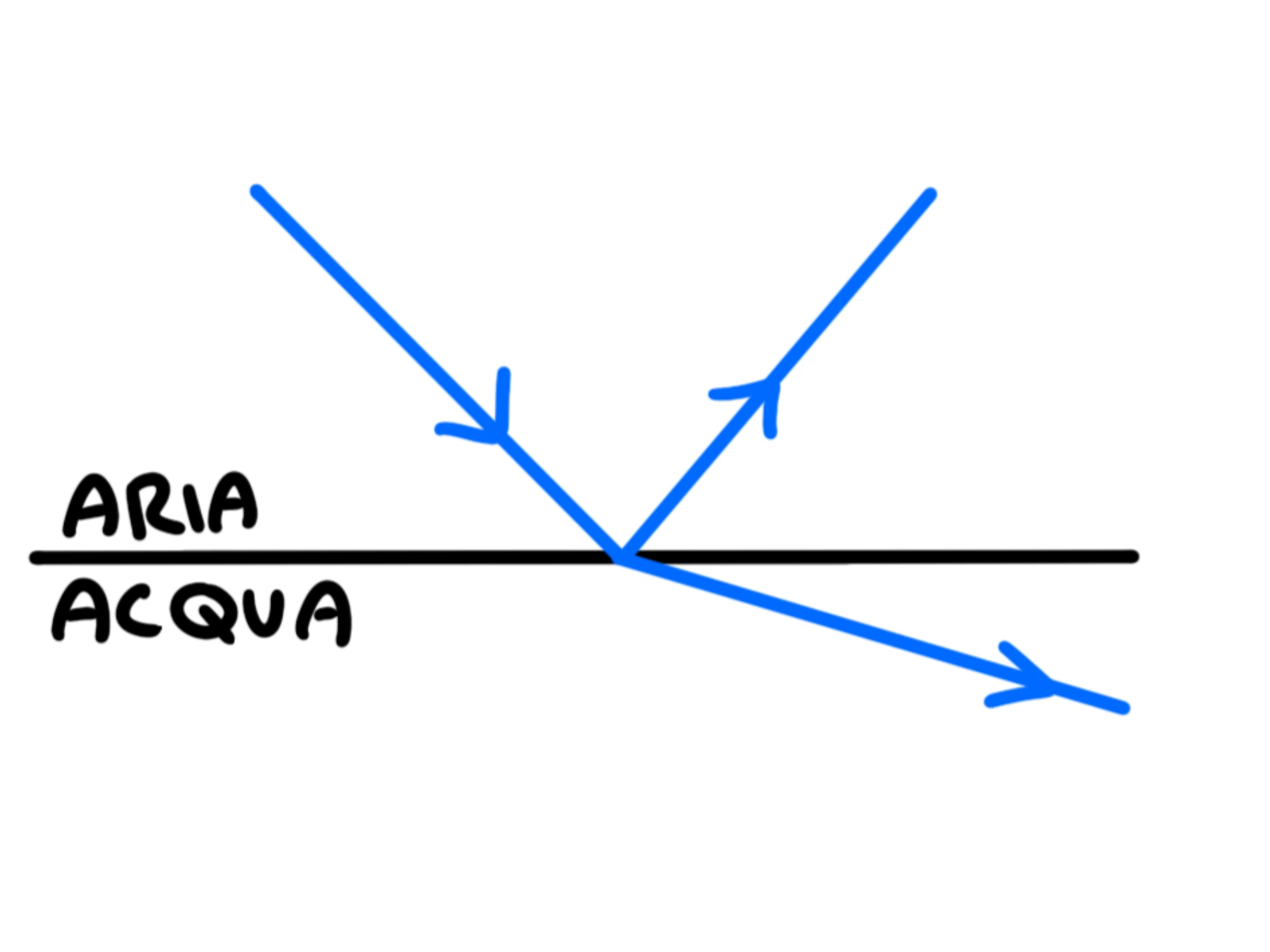
Nel caso in cui l'angolo di incidenza sia maggiore di avviene la riflessione totale.
Cioè siccome la luce non riesce ad essere rifratta nell'altro mezzo, in realtà la rifrazione non avviene proprio e tutta la luce viene riflessa:
