Rette tagliate da una trasversale

Se prendiamo due rette parallele e le intersechiamo con un'altra retta, chiamata trasversale , si formano degli angoli con proprietà particolari:

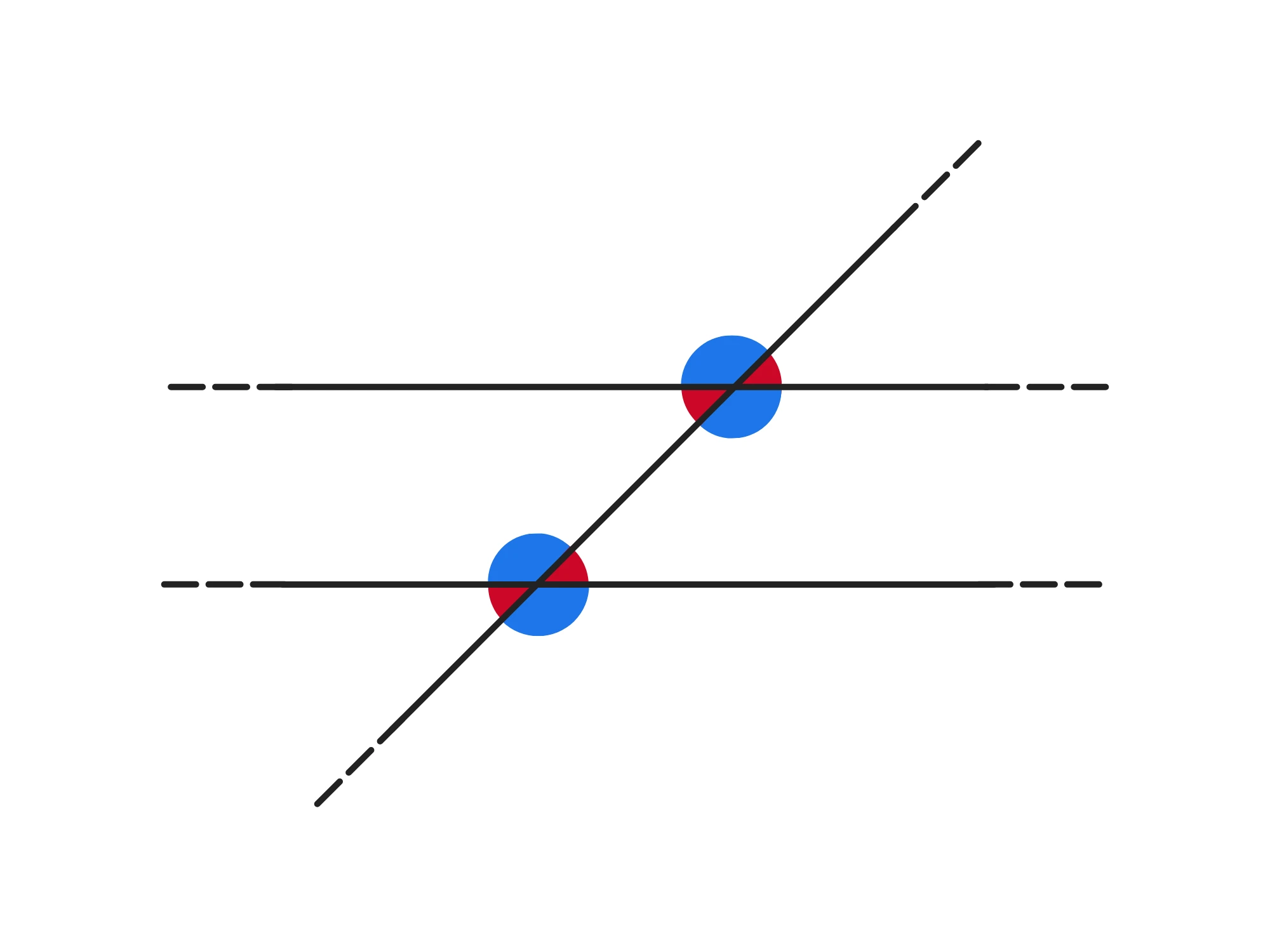
Nel grafico, tutti gli angoli blu sono uguali tra loro, tutti quelli rossi sono uguali tra loro ed ogni angolo rosso è supplementare (cioè la loro somma è $\displaystyle { 180^\circ }$ ) ad ogni angolo blu .

Possiamo formare vari tipi di coppie, oguna delle quali ha anche altre proprietà interessanti:

1. Angoli corrispondenti, ovvero gli angoli che si trovano nella stessa posizione, ossia $\displaystyle { (a, a’), }$ $\displaystyle { (b, b’), }$ $\displaystyle { (c, c’) }$ e $\displaystyle { (d,d'). }$ Tutti gli angoli corrispondenti sono uguali.

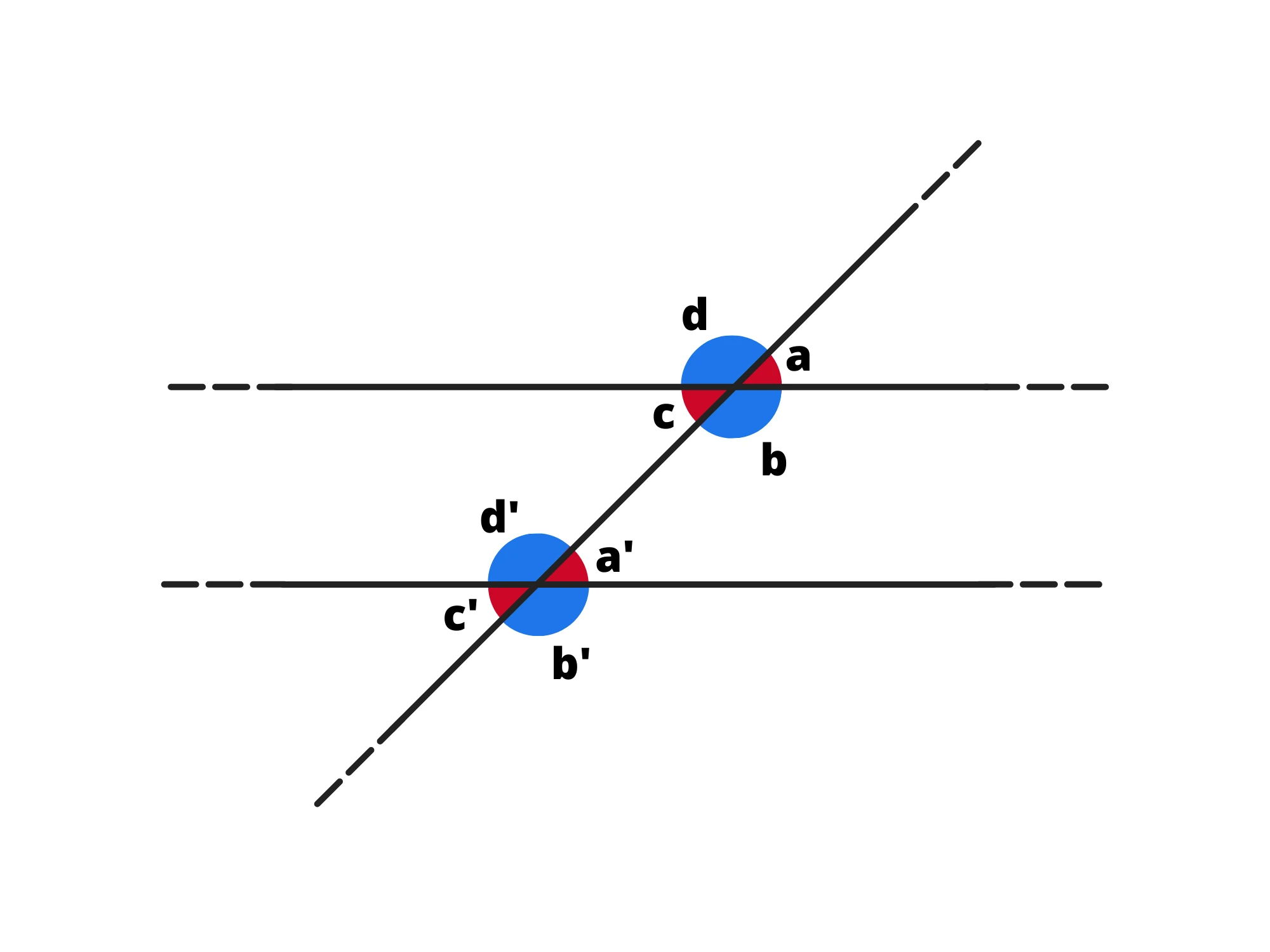
2. Angoli alterni interni, ovvero gli angoli che si alternano rispetto alla trasversale e che sono interni alle due rette, ossia $\displaystyle { (b, d’) }$ e $\displaystyle { (c, a’) }$. Tutti gli angoli alterni interni sono uguali.

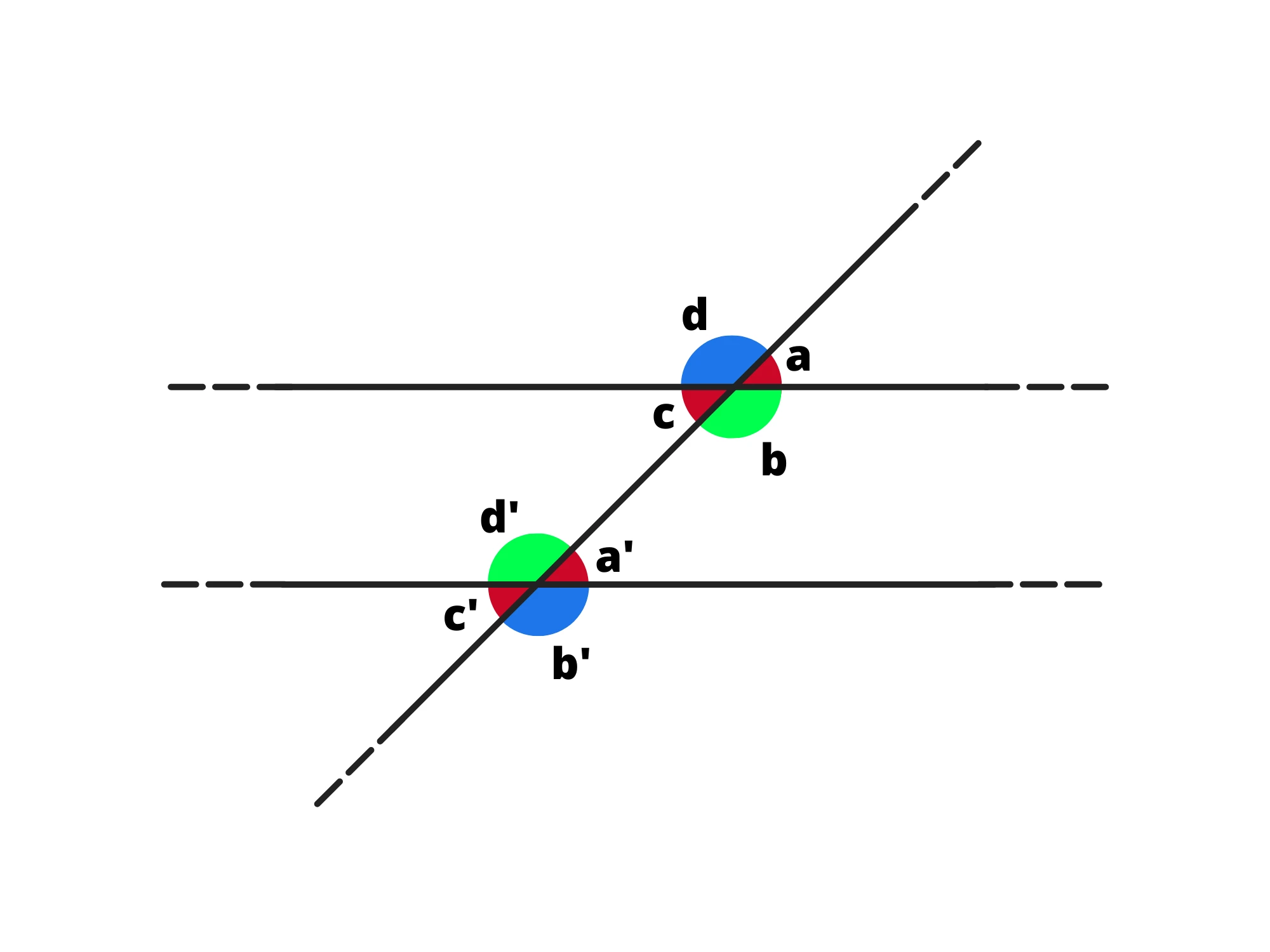
3. Angoli alterni esterni, ovvero gli angoli che si alternano rispetto alla trasversale e che sono esterni alle due rette, ossia $\displaystyle { (d, b’) }$ e $\displaystyle { (a, c’). }$ Tutti gli angoli alterni esterni sono uguali.

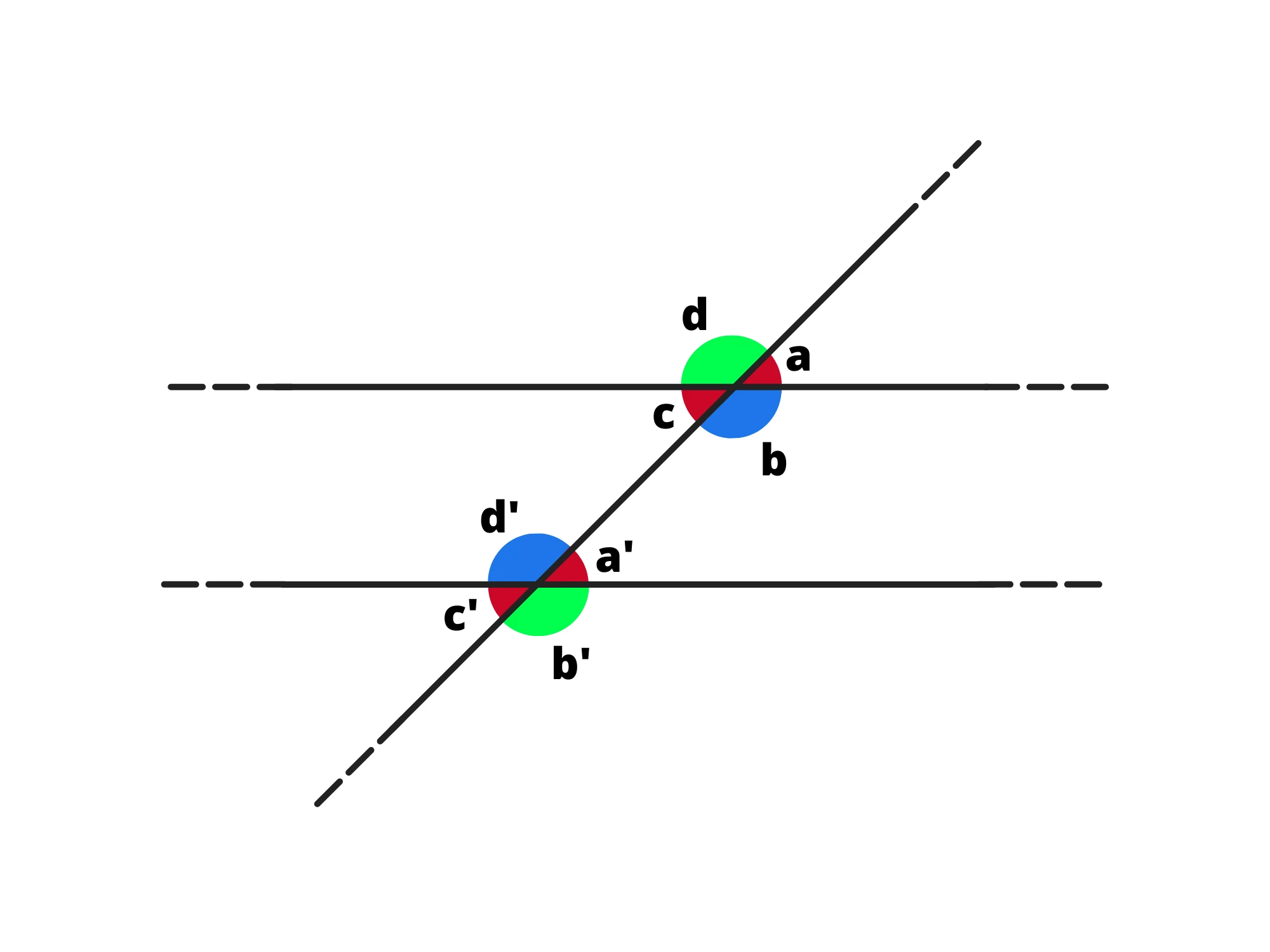
4. Angoli coniugati interni, ovvero gli angoli posti dallo stesso lato rispetto alla trasversale e che sono interni alle due rette, ossia $\displaystyle { (c, d’) }$ e $\displaystyle { (b, a’). }$ Tutti gli angoli coniugati interni sono supplementari.

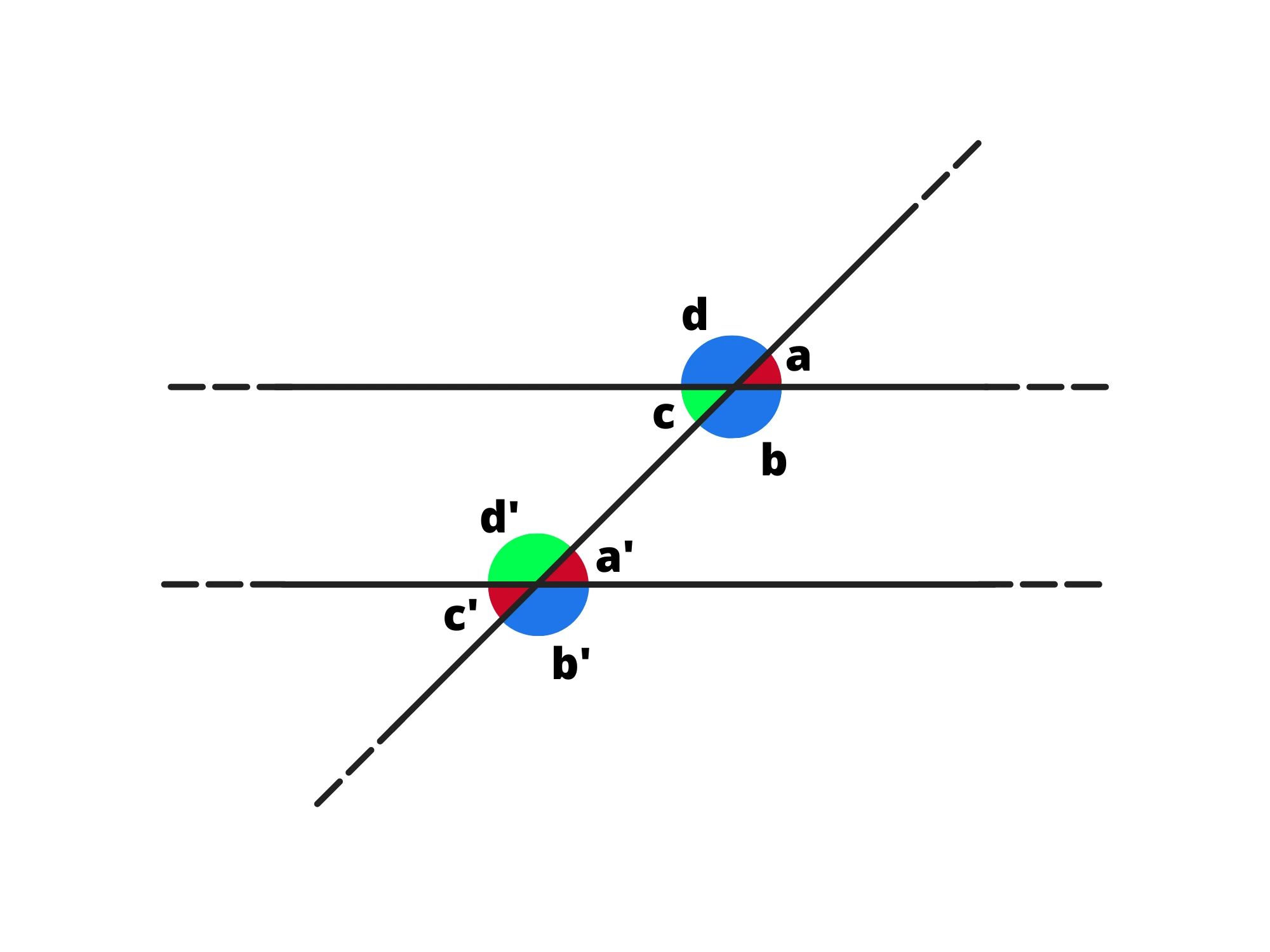
5. Angoli coniugati esterni, ovvero gli angoli posti dallo stesso lato rispetto alla trasversale e che sono esterni alle due rette, ossia $\displaystyle { (a, b’) }$ e $\displaystyle { (d, c’). }$ Tutti gli angoli coniugati esterni sono supplementari.

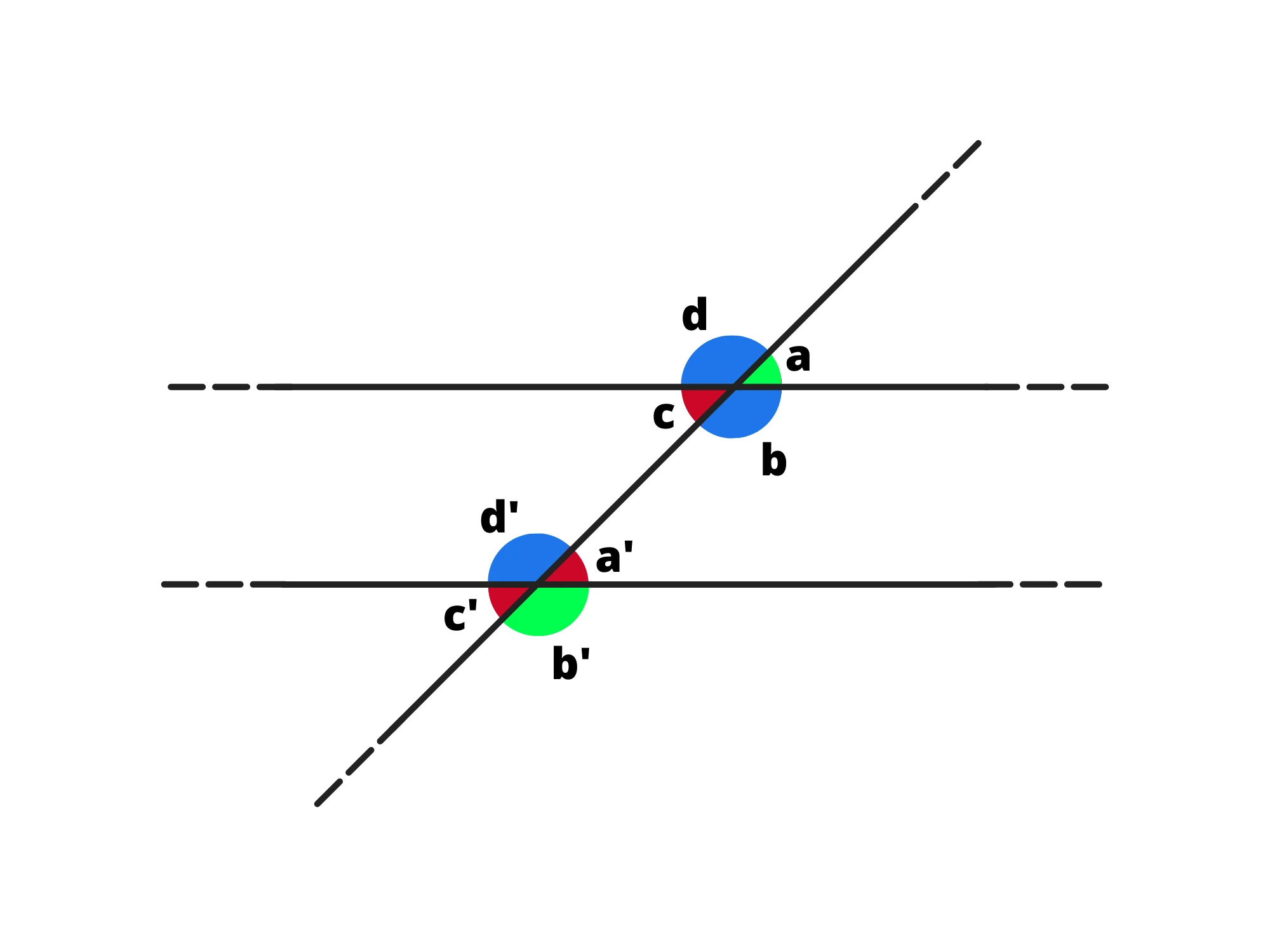
Grazie a questi angoli possiamo anche determinare se due rette sono parallele. Quindi se, ad esempio, sappiamo che due angoli alterni interni sono uguali, allora le due rette devono essere parallele; se dimostriamo che due angoli coniugati esterni sono supplementari, abbiamo anche dimostrato che le due rette sono parallele e così via.

! Attenzione Perché tutte queste proprietà siano valide le rette devono essere parallele.