Parallelogramma

Cos'è un parallelogramma?

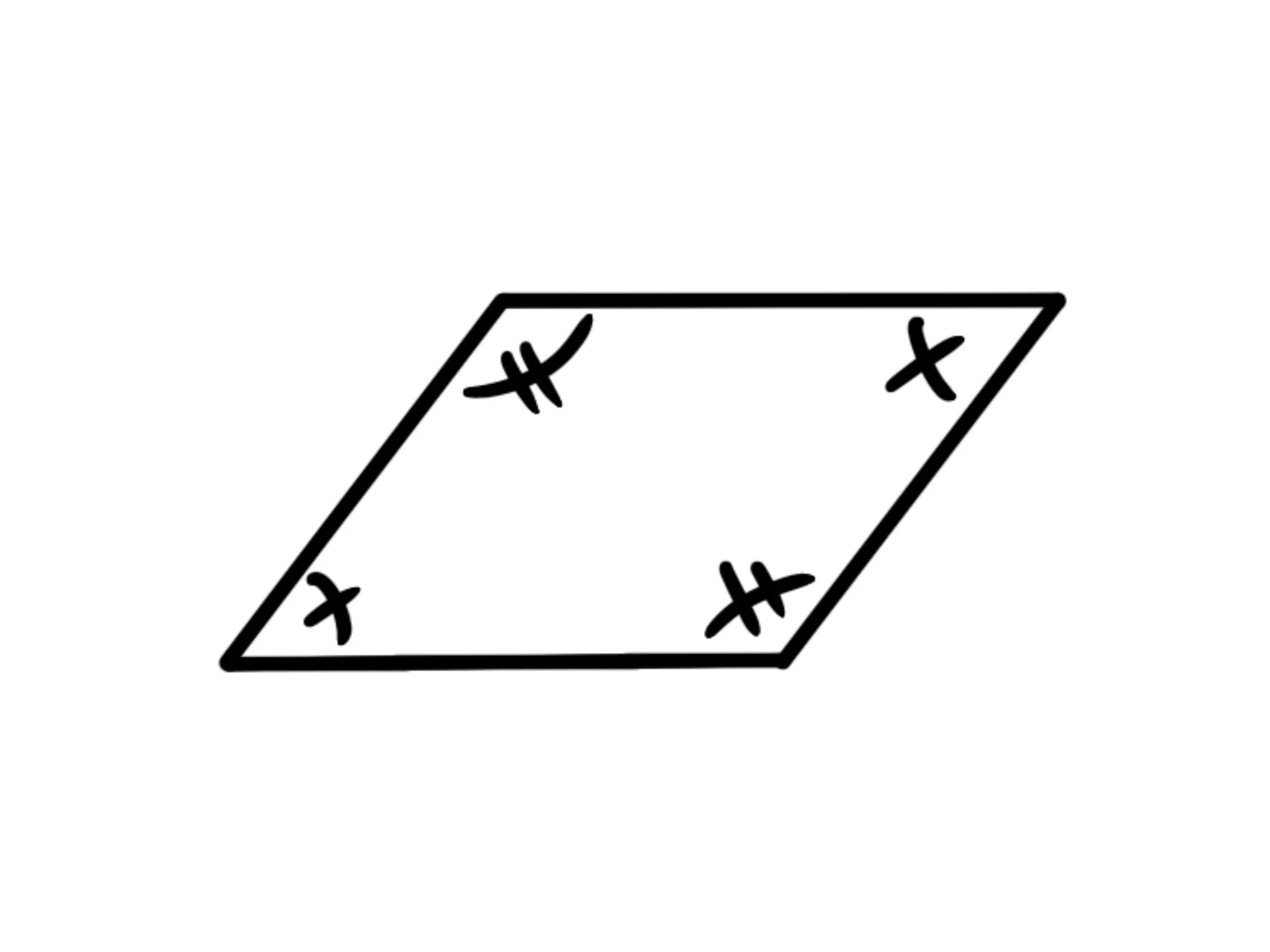
Un parallelogramma è un quadrilatero (cioè un poligono con 4 lati) che ha i lati opposti paralleli.

Ecco qualche esempio di parallelogramma:

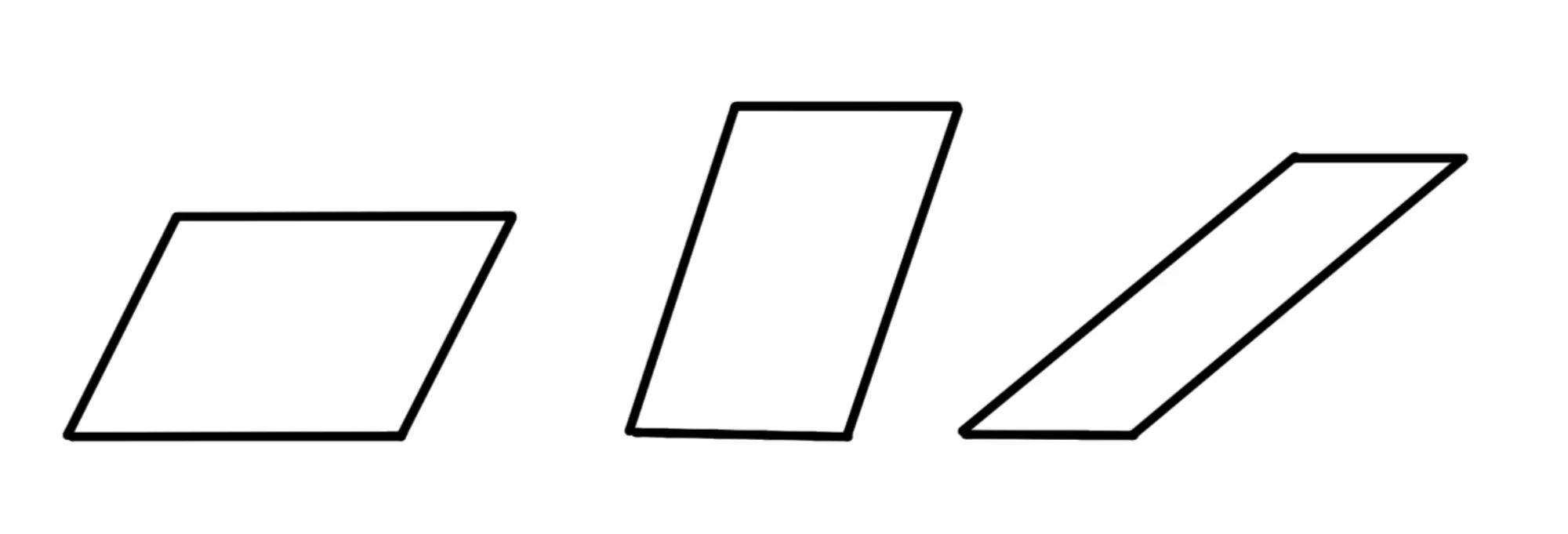
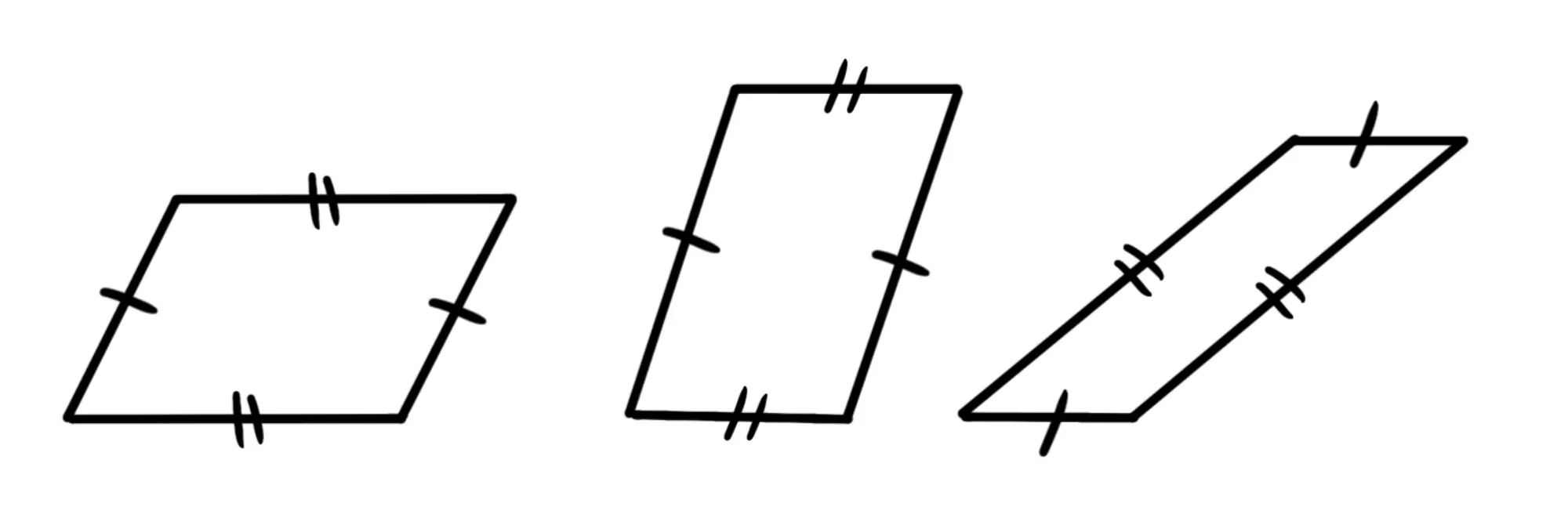
I lati opposti non soltanto sono paralleli, ma sono anche congruenti:

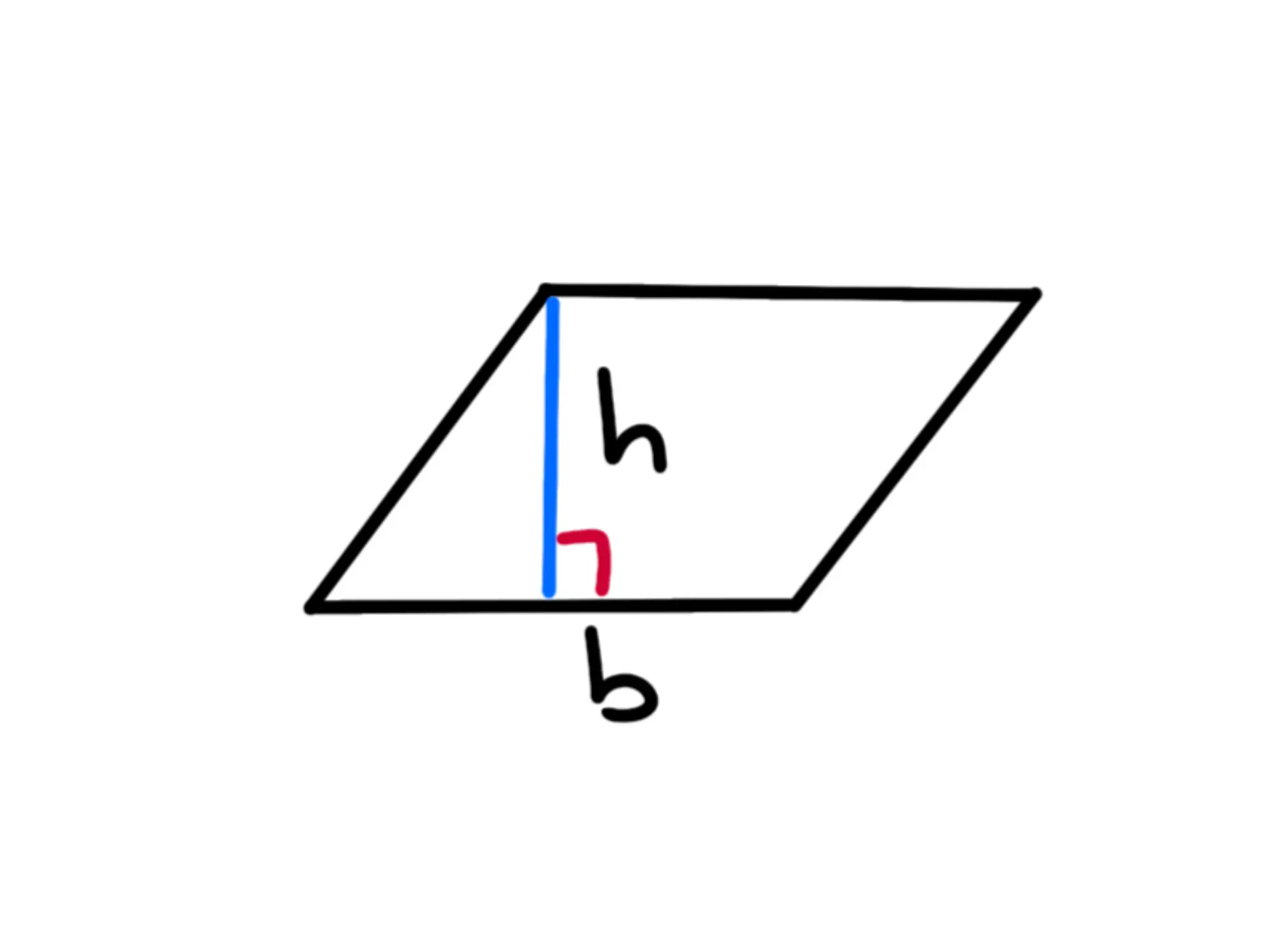
Chiamiamo uno dei quattro lati base e tracciamo il segmento che parte da uno dei due vertici opposti e che arriva perpendicolare alla base b e lo chiamiamo altezza e la indichiamo con la h:

Adesso siamo pronti per calcolare quanto vale il perimetro e l'area del parallelogramma:

Per il perimetro, se chiamiamo b la base e l il lato obliquo, siccome i lati sono a due a due congurenti, dovremo avere che il perimetro 2P vale:

2P = b+b+l+l

Cioè:

2P = 2(b+l)

Per calcolare l'area, invece, notiamo che quando tracciamo l'altezza si forma un triangolo:

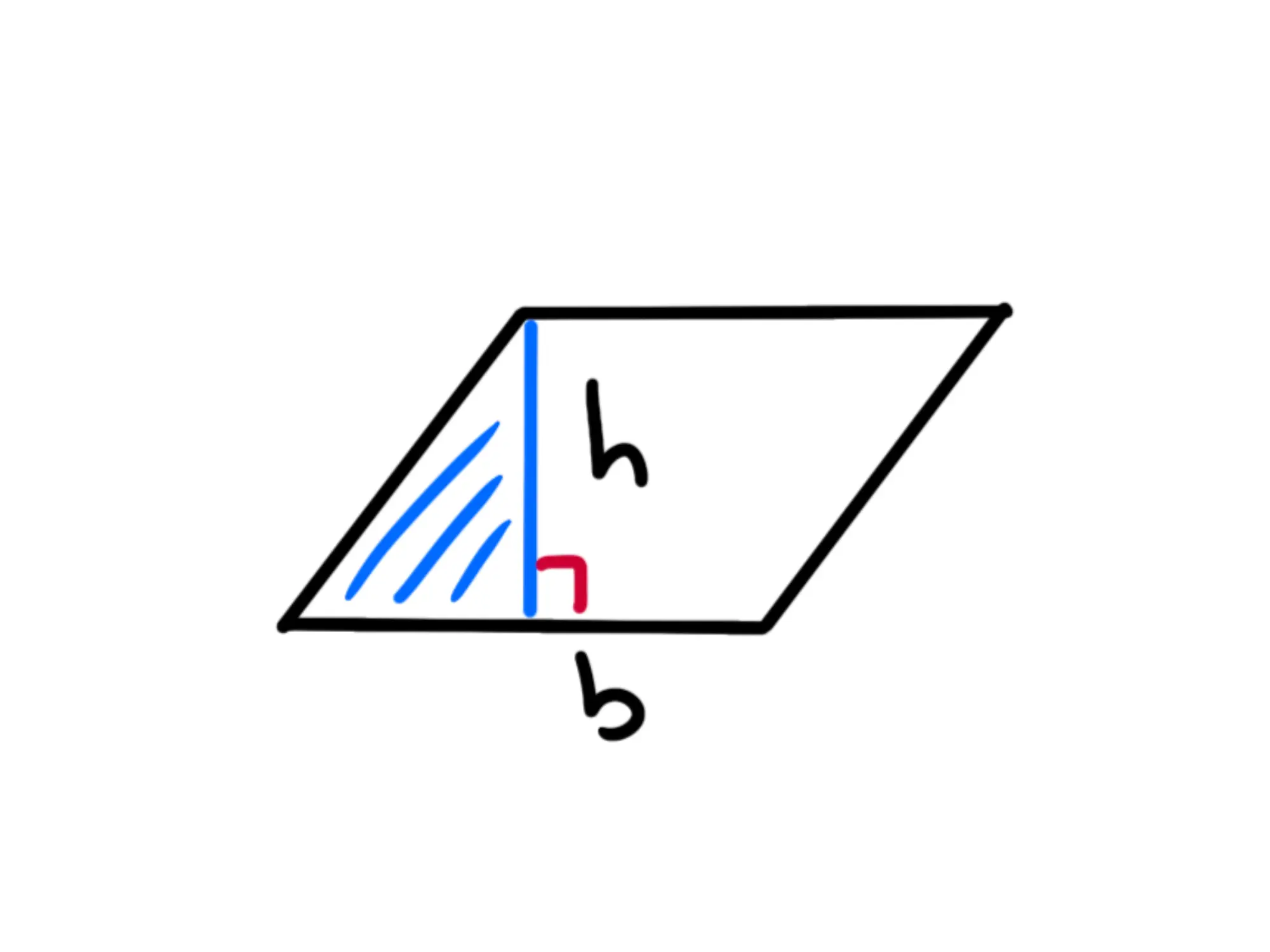
Notiamo che possiamo staccare questo triangolino e metterlo a destra in maniera da formare un rettangolo:

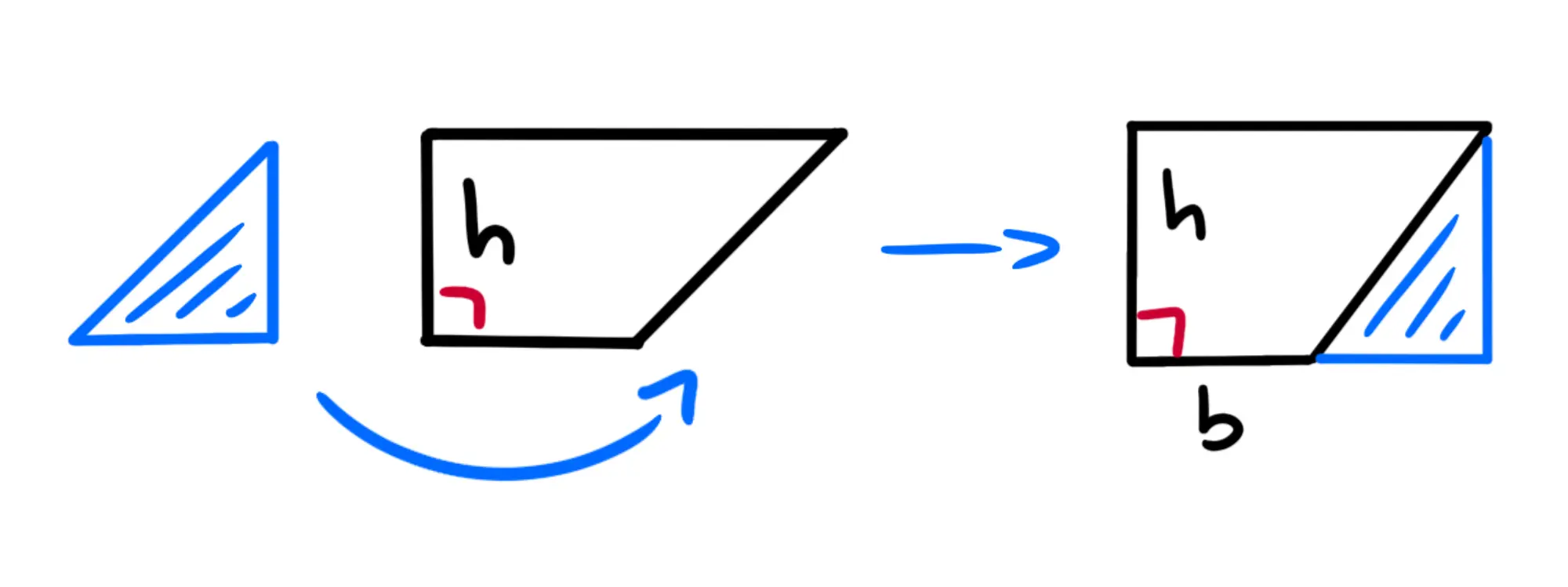
L'area del parallelogramma iniziale sarà uguale all'area di questo rettangolo, che è uguale alla base per l'altezza.

Dunque, dobbiamo avere che l'area A del parallelogramma è uguale a:

A = b\times h

Concludiamo facendovi notare che pure gli angoli opposti del parallelogramma sono congruenti: