Ciclo di Carnot

Cosa devo già sapere?

Da sapere:

Trasformazioni termodinamiche

Cicli termodinamici

Un ciclo termodinamico è una successione di trasformazioni termodinamiche che riportano il gas allo stato di equilibrio di partenza.

Cioè far fare un ciclo termodinamico ad un gas significa modificare il suo stato di equilibrio e poi riportarlo come stava prima.

Nel piano p-V, quindi, un ciclo apparirà come una linea chiusa che parte dallo stato iniziale A e infine ritorna in A, come nel grafico seguente:

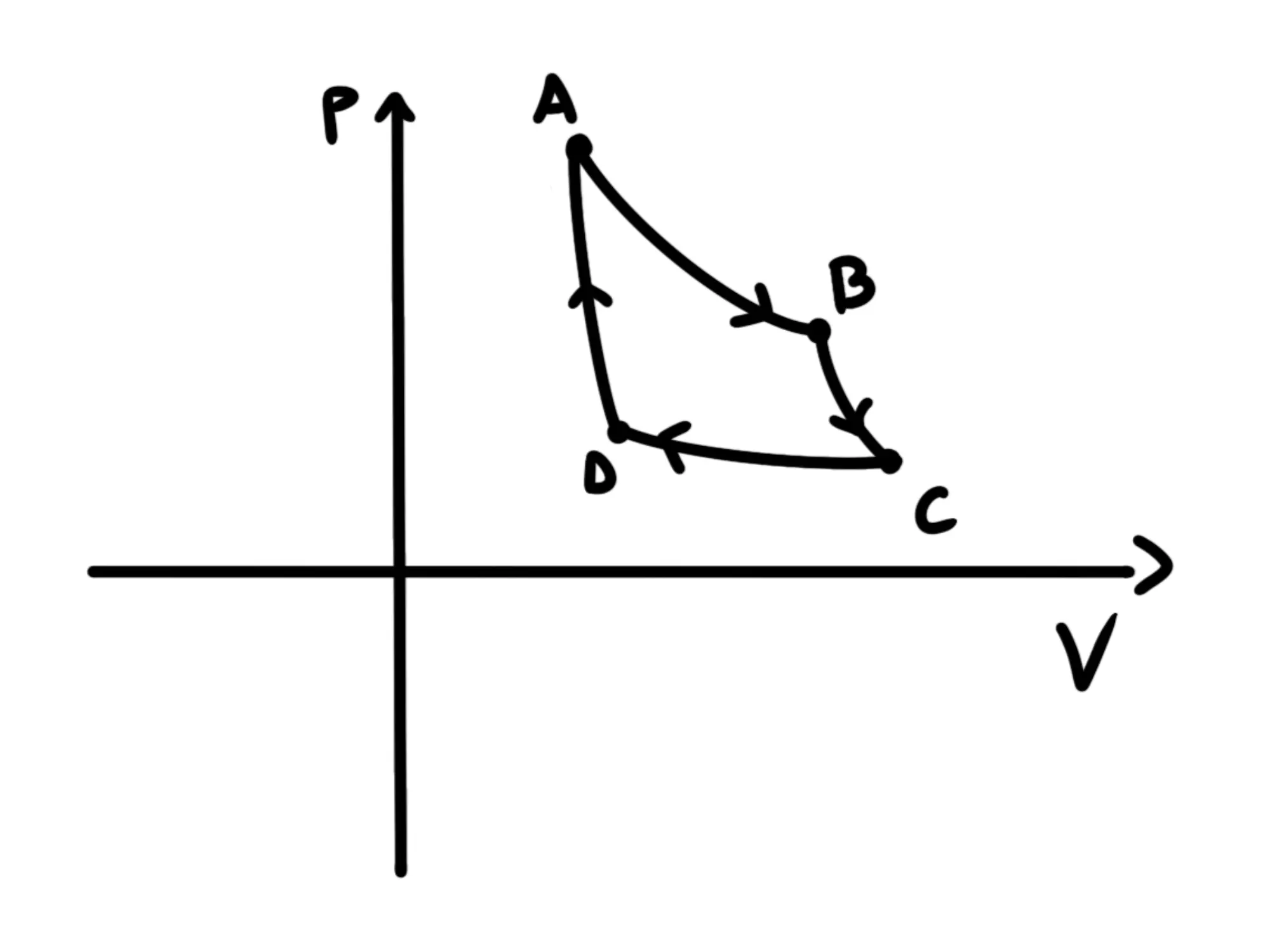
Perché ci interessano questi cicli?

Perché se ritornano al punto di partenza, vuol dire che posso farlo ricominciare quante volte voglio.

Quindi se per esempio applico un ciclo termodinamico ad un gas che muove un pistole il quale muove le ruote di un treno, allora posso far effettuare quel ciclo quante volte voglio e far muovere quindi il treno per lunghissimi tratti.

Esiste una caso particolare di ciclo termodinamico che è formato da due trasformazioni adiabatiche e due isoterme e viene chiamato ciclo di Carnot.

Vediamolo più nel dettaglio:

Ciclo di Carnot

Come abbiamo detto nel capitolo precedente, un ciclo di Carnot è un ciclo termodinamico formato da due trasformazioni adiabatiche e due isoterme.

Quindi il suo grafico nel piano p-V apparirà come il seguente:

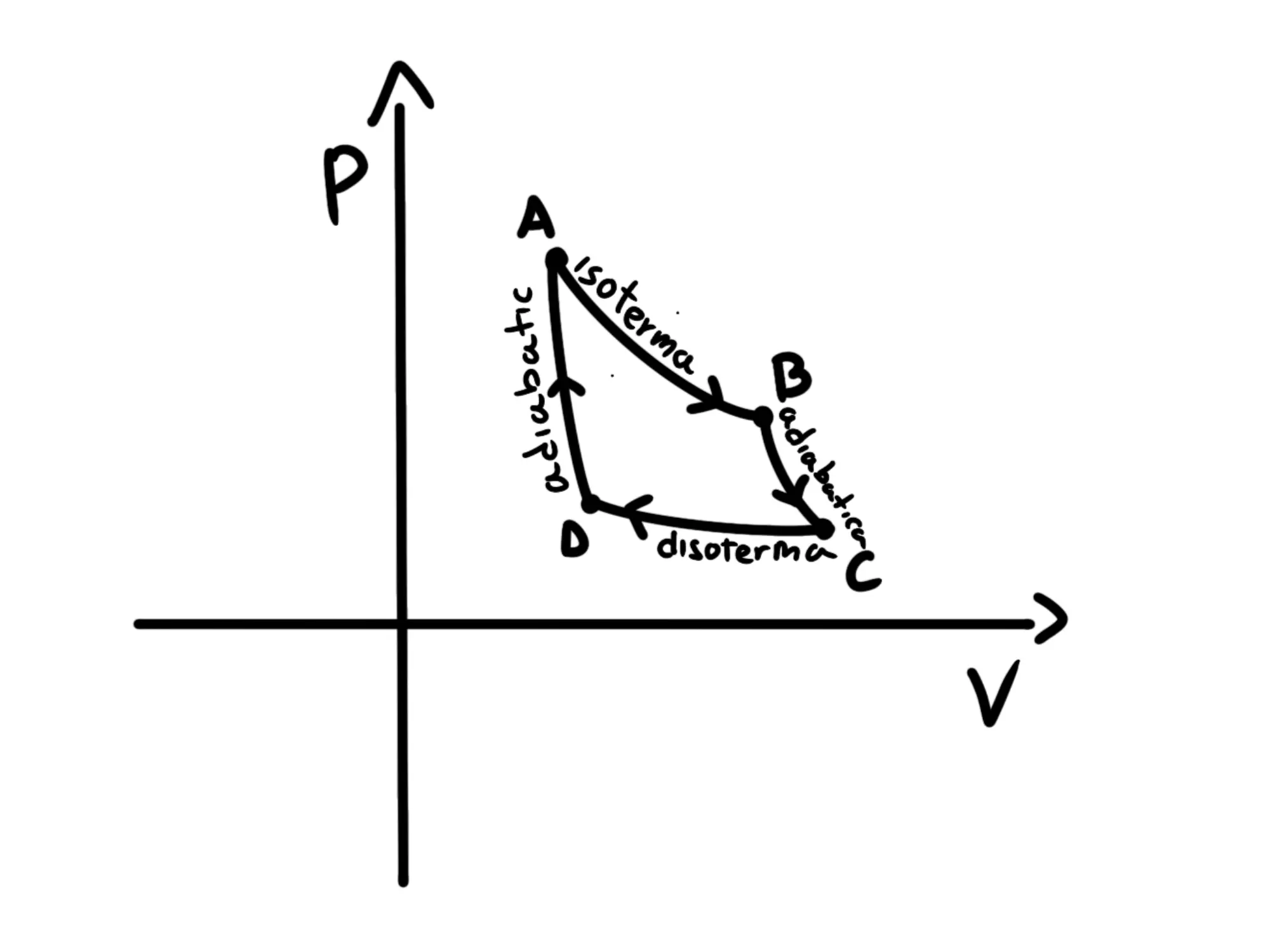
Per realizzare questo ciclo abbiamo dunque bisogno di due sorgenti:

Una calda che dia calore al gas durante l'espansione isoterma (il tratto A \to B del nostro grafico).

Una fredda che prenda calore dal gas durante la contrazione isoterma (il tratto C \to D del nostro grafico).

Queste due sorgenti avranno dunque due termerature T_1 (calda) e T_2 (fredda).

Si può dimostrare, usano gli integrali (L = \int_A^B p \, dV), che l'area sotto il grafico di una trasformazione è uguale al modulo del lavoro effettuato.

Dico modulo perché dobbiamo stare attenti al segno: se ci stiamo muovendo verso destra nel piano (come nelle trasformazioni A\to B e B\to C), allora il volume sta aumentando, quindi il gas provoca uno spostamentento e il lavoro che fa è positivo.

Se invece ci stiamo muovendo verso sinistra (come nelle trasformazioni C\to D e D \to A), allora il volume sta diminuendo, quindi il gas sta venendo compresso, dunque sta venendo fatto lavoro sul gas e quindi sarà negativo.

Adesso segnamo con il blu le aree positive e con il rosso quelle negative:

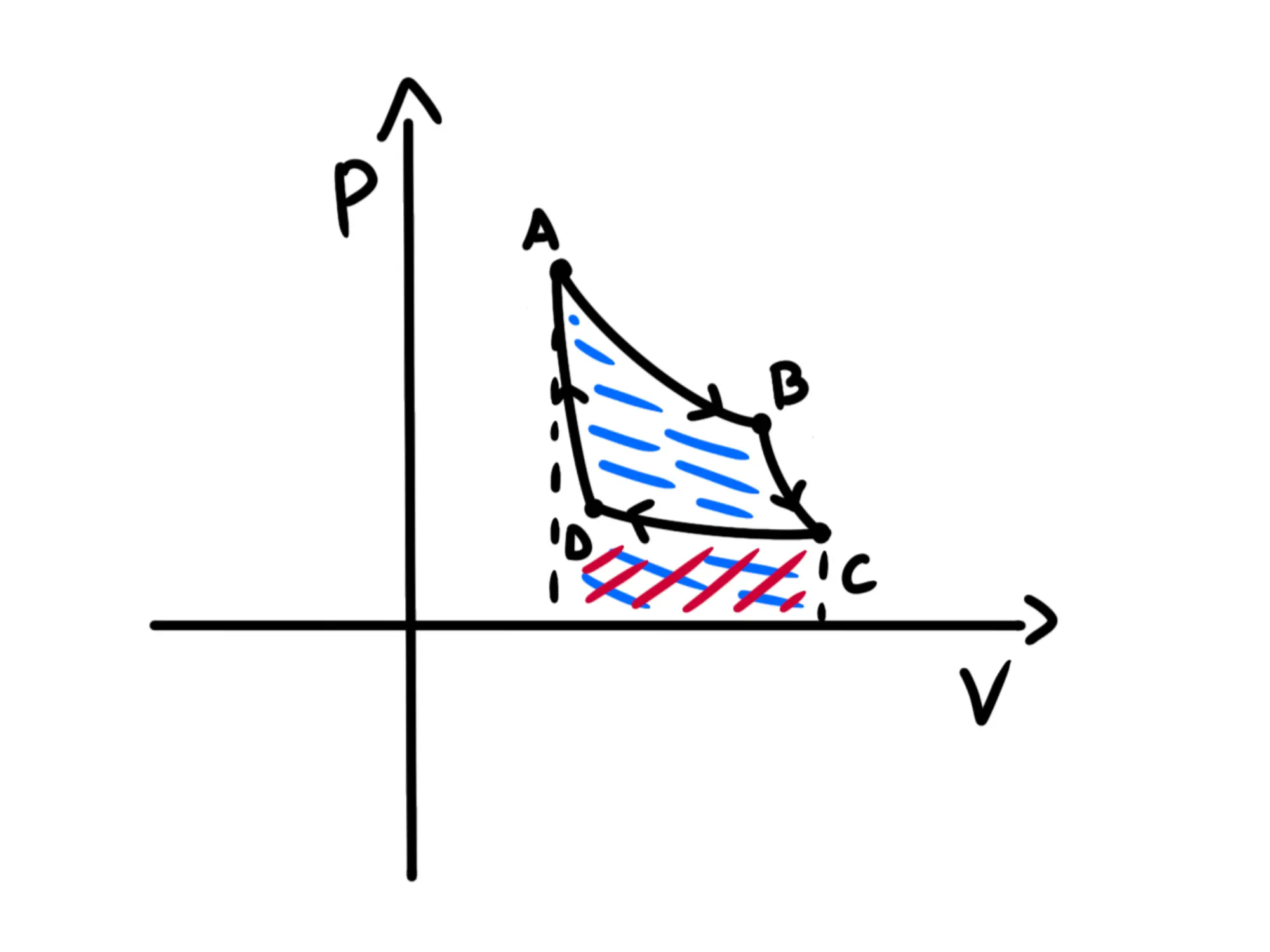
Il sottografico rosso delle trasformazioni C\to D e D\to A si semplificano con delle parti delle aree delle trasformazioni A\to B e B\to C. Semplificandole otteniamo questo:

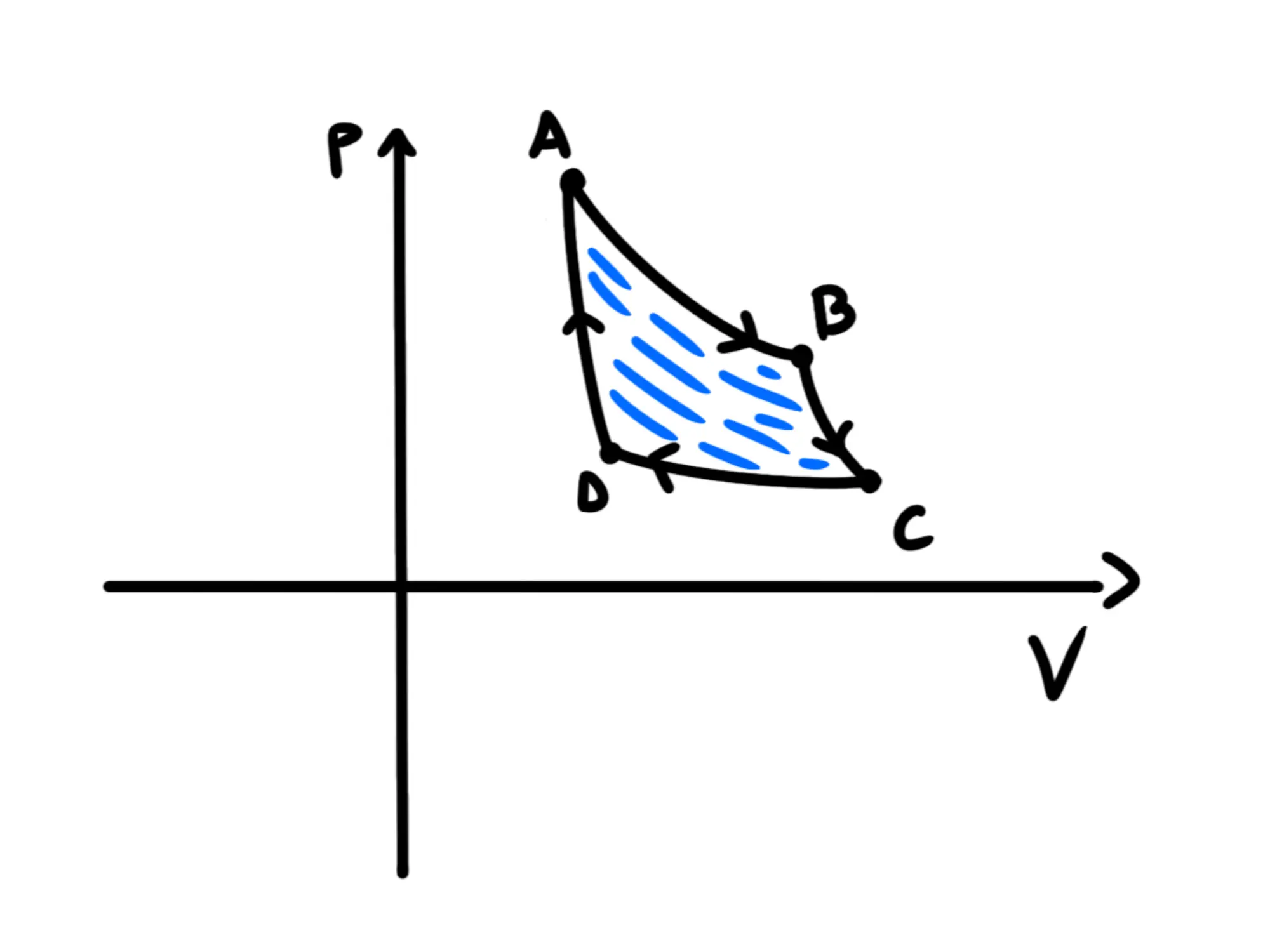
L'area è blu, quindi è positiva. Perciò il lavoro totale fatto da un ciclo di Carnot è sempre positivo ed è uguale all'area della figura formata dalle quattro trasformazioni.

Maggiore è quell'area e maggiore è il lavoro che la macchina termica fa in ogni ciclo.

Per farle fare questo lavoro abbiamo dovuto dare energia alla macchina tramite calore. Quando avvengono questi scambi di calore?

Abbiamo detto che le trasformazioni B\to C e D\to A sono adiabatiche, quindi, per definizione, durante esse non ci sta alcuno scambio di calore con l'esterno.

Quindi gli scambi avvengono tutti in A\to B e C \to D.

Si trattano di due trasformazioni isoterme, dunque il calore può essere calcolato come nRT\ln({V_f \over V_i}).

Nella trasformazione A\to B, il volume finale (V_f) è maggiore di quello finale (V_i), quindi il logaritmo presente nella formula sarà positivo e quindi il calore è positivo, il che significa che la macchina termina sta acquisendo calore dall'ambiente esterno.

Invece, nella trasformazione C\to D, il volume sta diminuendo, quindi quel logaritmo avrà un argomento minore di 1 e sarà dunque negativo, perciò pure il calore sarà negativo. Questo significa che la macchina termica sta cedendo calore all'ambiente esterno.

Quindi, cosa sta succedendo?

Noi stiamo dando energia tramite calore alla macchina, per esempio bruciando del carbone in una locomotiva. La macchina termica prenderà quest'energia e in parte la userà per fare del lavoro mandando avanti il treno, in parte però la rilascerà cedendo calore all'esterno riscaldando l'aria, il treno o quello che ha intorno.

A noi, solitamente, serve poco riscaldare l'aria intorno al treno, mentre ci interessa farlo muovere. Quindi vogliamo che questo processo sia efficiente, cioè che perda poca energia tramite calore.

Vogliamo quindi calcolare quanta parte del calore che assorbe riesce a trasformare in lavoro, cioè il rapporto tra il lavoro compiuto (L) e il calore assorbito Q_{as}.

Chiamiamo questo rapporto rendimento e lo indichiamo con la lettera greca \eta (eta).

\eta = {L \over Q_{as}}

Più sarà vicino ad 1 e più la macchina sarà efficiente, mentre più sarà vicino a 0 e meno sarà efficiente.

La macchina rilascia tutto il calore assorbito tramite il lavoro che compie e il calore che cede (Q_{ce}), dunque la somma dei moduli di quest'ultimi due dovrà essere uguale al modulo del calore assorbito.

|Q_{as}| = |L| + |Q_{ce}|

(mettiamo i moduli perché potrebbero avere segni negativi per la notazione che usiamo normalmente, mentre in questo caso stiamo vedendo alla quantità di energia scambiata, indipendentemente se tramite calore o lavoro).

Da questo otteniamo:

|L| = |Q_{as}| - |Q_{ce}|

Sostituendo nella formula otteniamo:

\eta = {|Q_{as}| - |Q_{ce}| \over |Q_{as}|}

Sappiamo però che Q_{as} sarà positivo perché si tratta di calore assorbito dalla macchina, mentre Q_{ce} sarà negativo perché si tratta di calore ceduto dalla macchina. Quindi possiamo togliere i moduli e cambiare il segno di Q_{ce}:

\eta = {Q_{as} + {Q_{ce}} \over Q_{as}}

Adesso semplifichiamo la frazione:

\eta = {Q_{as}\over Q_{as}} +{Q_{ce} \over Q_{as}}

\eta = 1 + {Q_{ce} \over Q_{as}}

Ricordiamoci che questi calori sono scambiati durante due trasformazioni isotermiche a temperatura T_2 (fredda, quella di Q_{ce}) e T_1 (calda, quella di Q_{as}).

Come abbiamo visto prima, possiamo calcolare questi due calori usando la formula Q = nRT \ln({V_f \over V_i}).

Sostituendo e inserendo le opportune lettere, otteniamo:

\eta = 1 + {nRT_2 \ln({V_D \over V_C}) \over nRT_1\ln({V_B\over V_A})}

\eta = 1 + {T_2 \ln({V_D \over V_C}) \over T_1 \ln({V_B \over V_A})}

Si può dimostrare, ma non lo vedremo in questa lezione, che {\ln({V_D \over V_C}) \over \ln({V_B\over V_A})} = -1. Sostituendo otteniamo:

\eta = 1 - {T_1 \over T_2}

Quindi, per ottenere il rendimento migliore possibile, il rapporto {T_1 \over T_2} deve essere il più piccolo possibile.

Per farlo abbiamo due modi: o aumentiamo la temperatura della sorgente calda (alzando così in alto A e B), oppure abbassando la temperatura della sorgente fredda (abbassando così C e D).

La temperatura, però, essendo misurata in Kelvin non può essere abbassata all'infinito perché non può essere negativa. Infatti la seconda legge della termodinamica ci dice che è impossibile raggiungere lo 0 assoluto (cioè 0 Kelvin).

Quindi il rapporto non sarà mai uguale a 0 e quindi \eta sarà sempre minore di 1.

Per questo la seconda legge della termodinamica può essere enunciata pure come:

Non può esistere alcuna macchina termica con un rendimento pari ad 1.

Sapendo quanto vale il rendimento \eta, dalla sua definizione possiamo calcolare il lavoro compiuto con la formula inversa:

L = \eta Q_{as}