Cerchio

Cosa sono il cerchio e la circonferenza?

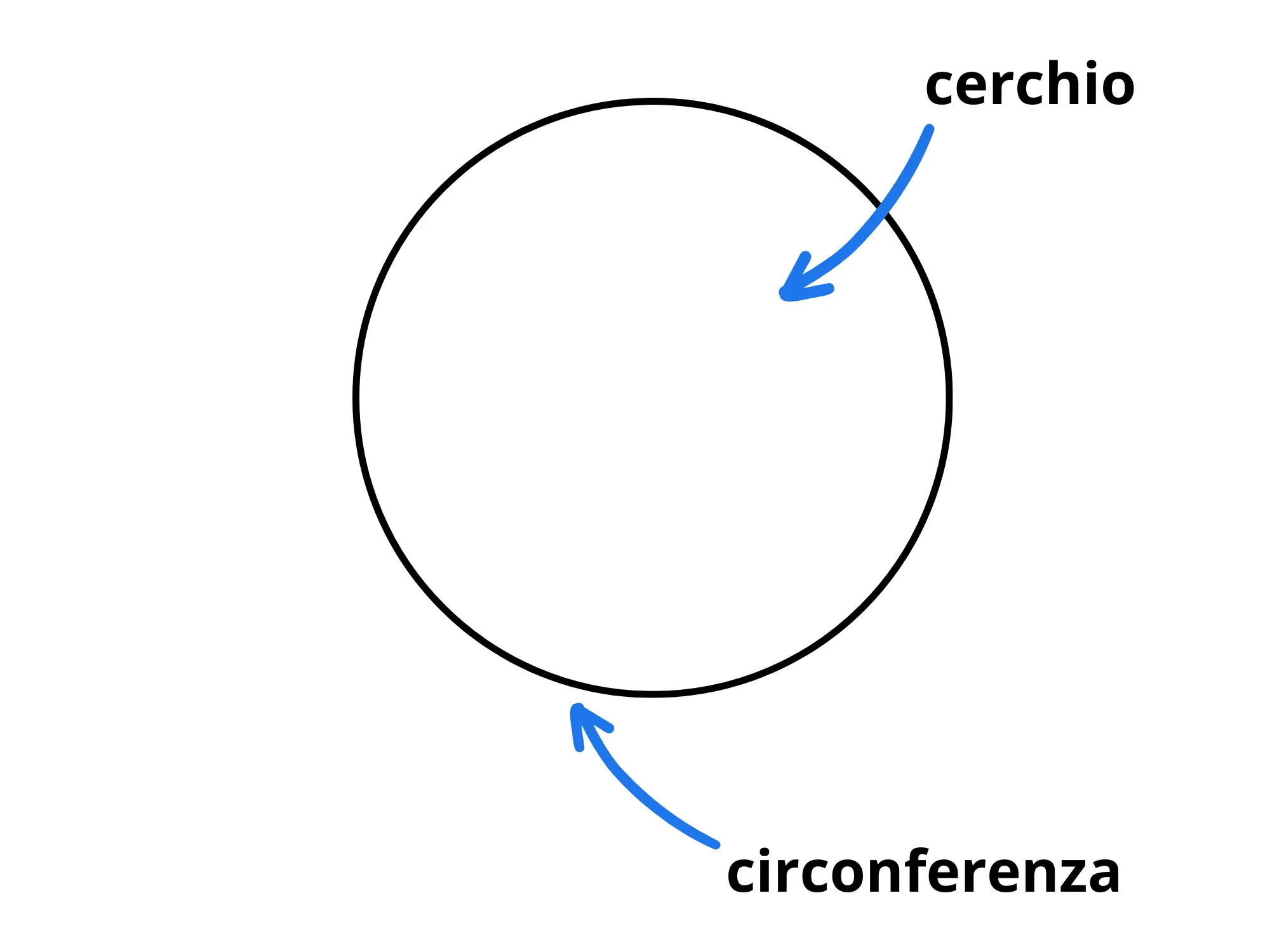
Partiamo da un concetto fondamentale: la circonferenza e il cerchio sono due cose diverse:

La circonferenza, infatti, viene definita come l'insieme dei punti equidistanti da un punto fisso chiamato centro.

Il cerchio, invece, viene definito come la parte di piano delimitata dalla circonferenza.

In altre parole, la circonferenza è solo il contorno mentre il cerchio contiene anche l'interno.

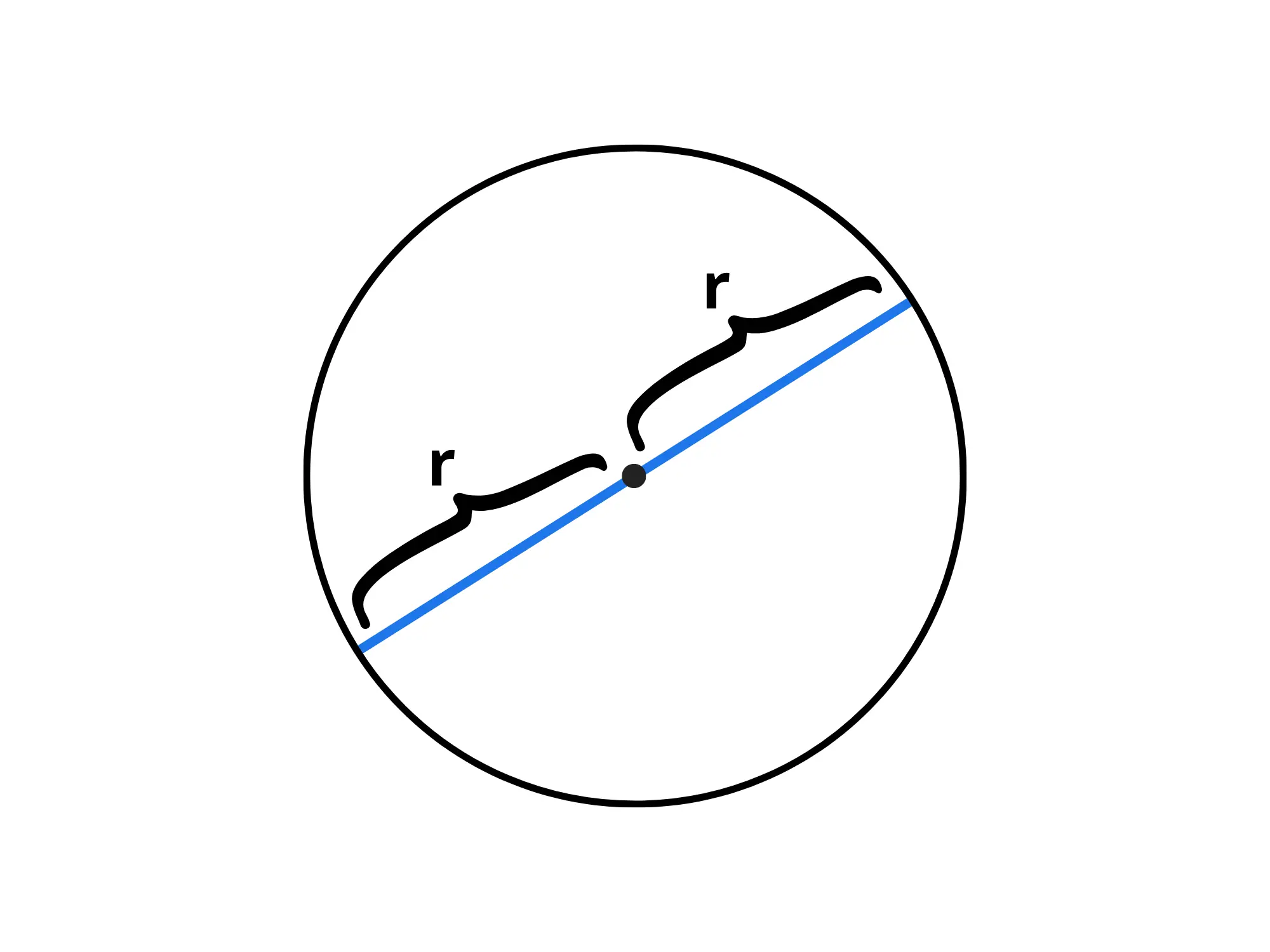
Abbiamo detto che tutti i punti sulla circonferenza distano ugualmente dal centro, questa distanza viene chiamata raggio .

Un segmento che congiunge due punti della circonferenza passando per il centro viene chiamato diametro :

Siccome la distanza tra un punto della circonferenza e il centro è sempre uguale al raggio, il diametro dovrà essere uguale al doppio del raggio.

Probabilmente vi ricorderete dalle elementari la formula per calcolare la lunghezza della circonferenza (Circonferenza spesso si abbrevia $\displaystyle { CRF }$ ) conoscendo il raggio.

Infatti, se chiamiamo r il nostro raggio, dovremo avere:

Quel simbolo strano, $\displaystyle { \pi, }$ è la lettera greca corrispondente alla nostra p, per questo lo chiamiamo pi greco .

$\displaystyle { \pi }$ è un numero irrazionale, questo significa che non potremo mai scriverlo come una frazione, né come un numero decimale finito o un numero decimale periodico. Possiamo solo approssimarlo o lasciarlo così.

Le prime cifre del pi greco sono:

Quel simbolo, $\displaystyle { \approx }$ , significa circa. Quante cifre del pi greco dovete imparare a memoria? Dipende da quanta precisione volete, ma solitamente basta ricordarsi le prime tre, ovvero $\displaystyle { 3,14. }$

Quindi, se ad esempio abbiamo un cerchio di raggio $\displaystyle { 4 cm, }$ sappiamo subito che la circonferenza sarà lunga:

$\displaystyle { CRF = 2\pi \cdot 4cm = 8\pi cm }$

Come si calcola l’area del cerchio conoscendo il raggio? Ci basta usare la seguente formula:

Dove, appunto, $\displaystyle { A }$ sarebbe l'area del cerchio.

Nell'esempio di prima, quindi, l'area del cerchio era uguale a:

$\displaystyle { A = \pi (4cm)^2 = 16\pi cm^2 }$

Prima di passare a studiare alcuni teoremi importanti sul cerchio, vediamo qualche altra definizione:

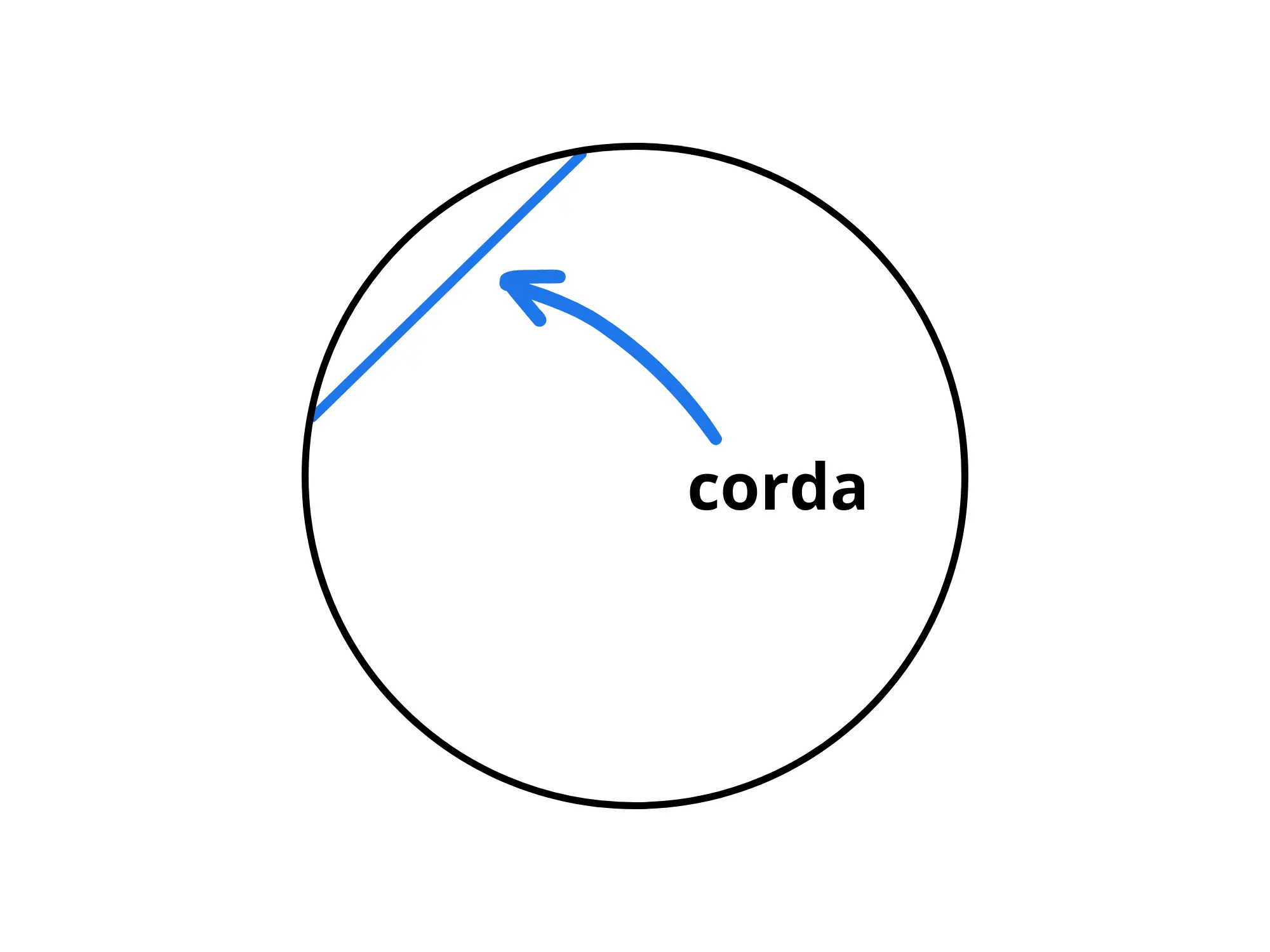
Una corda è un segmento che unisce due punti sulla circonferenza:

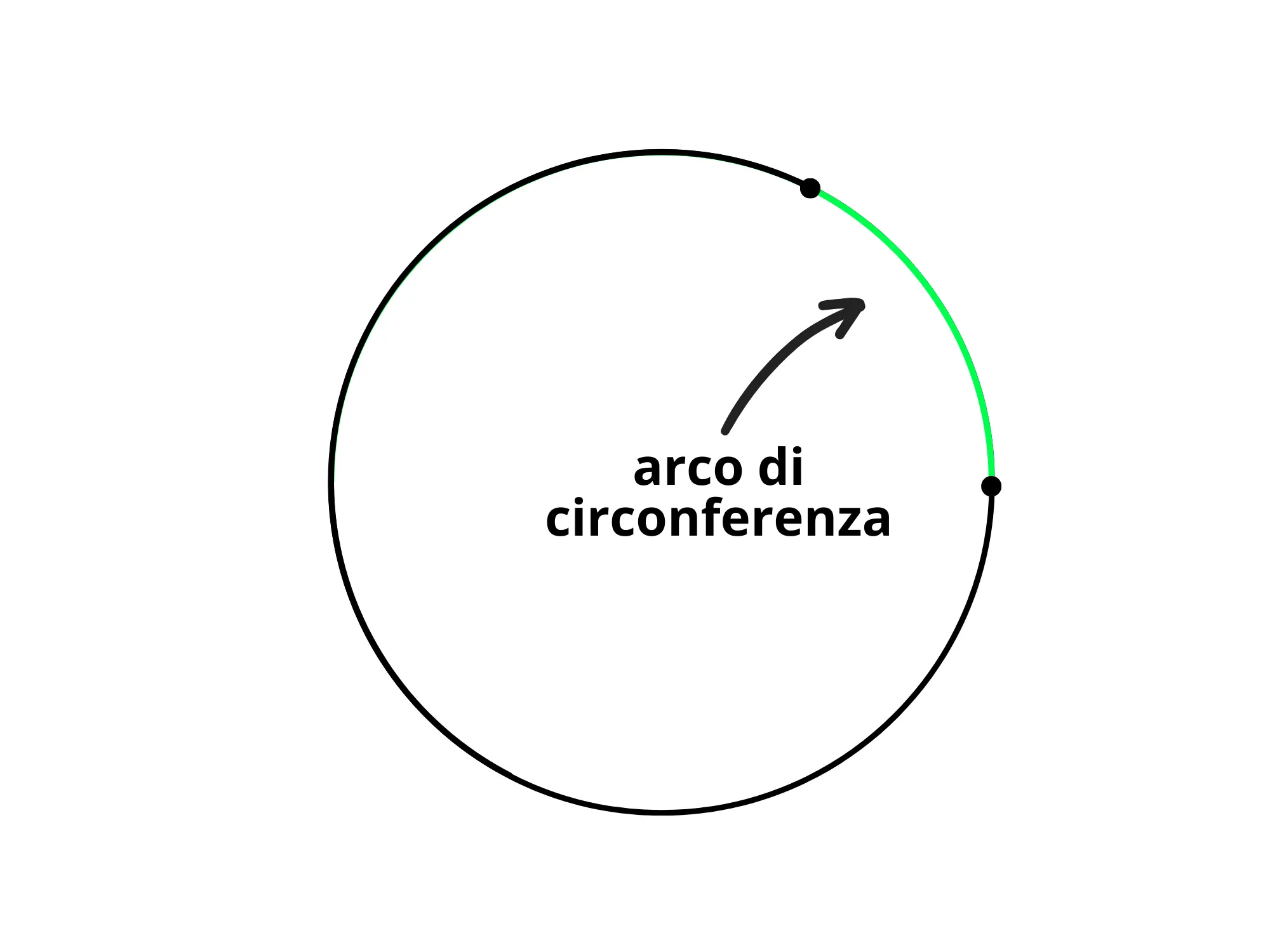
Un arco di circonferenza è una parte della circonferenza delimitata da due sue punti:

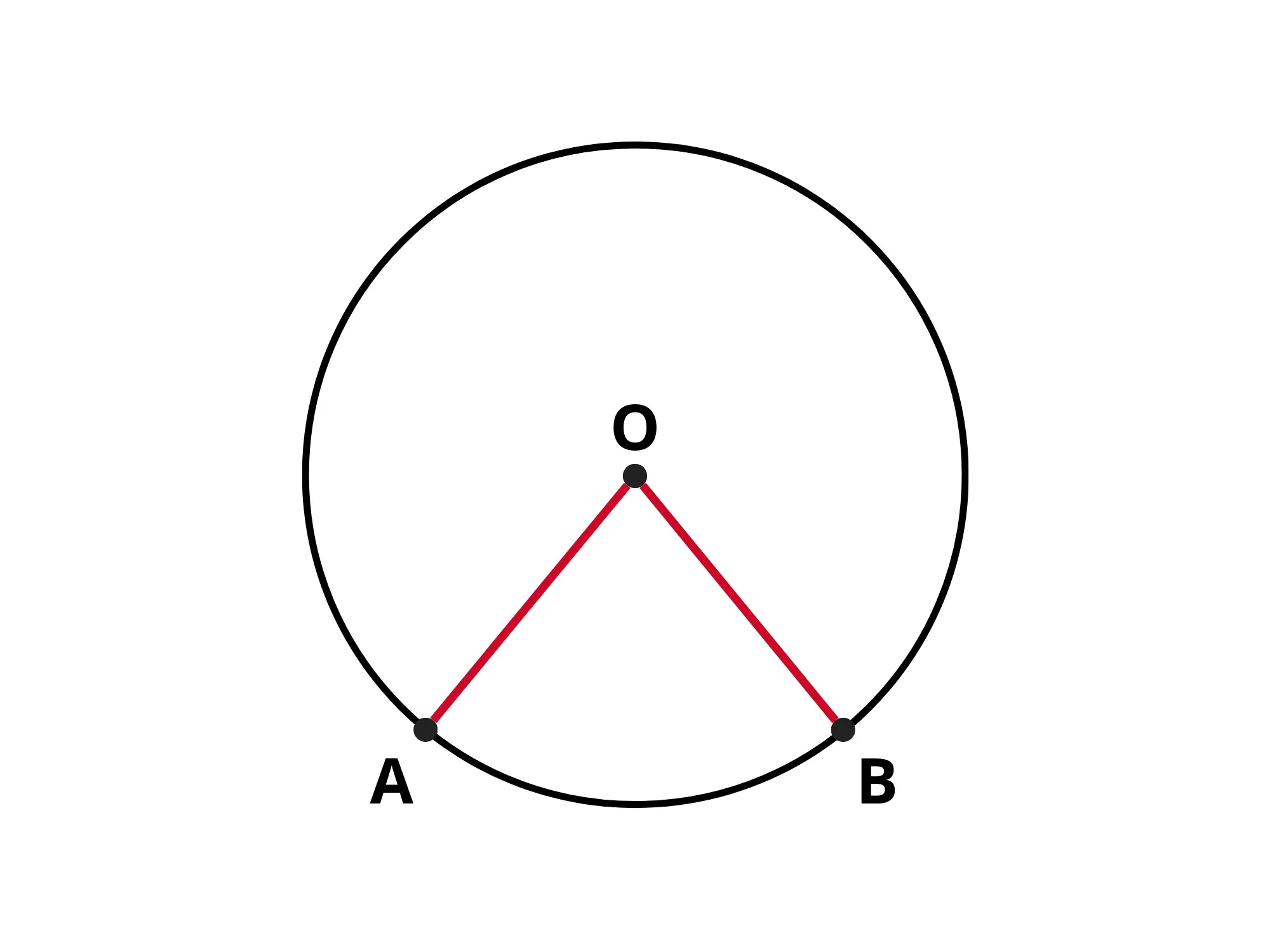
Un settore circolare è una parte di cerchio delimitata da un arco di circonferenza e dai due raggi che congiungono il centro con le due estremità dell'arco:

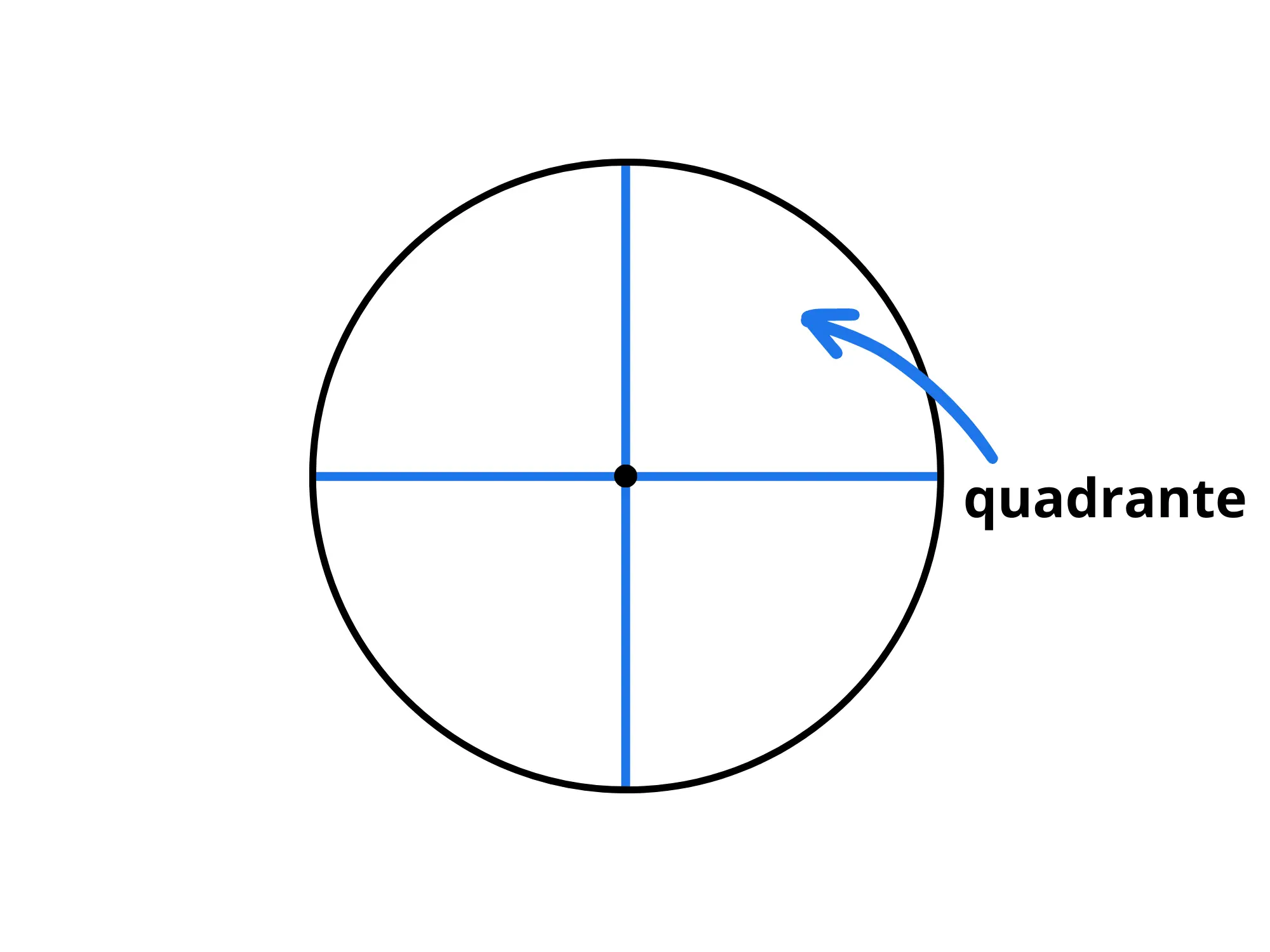
Se dividiamo il cerchio in $\displaystyle { 4 }$ parti uguali, ognuna di esse viene chiamata quadrante:

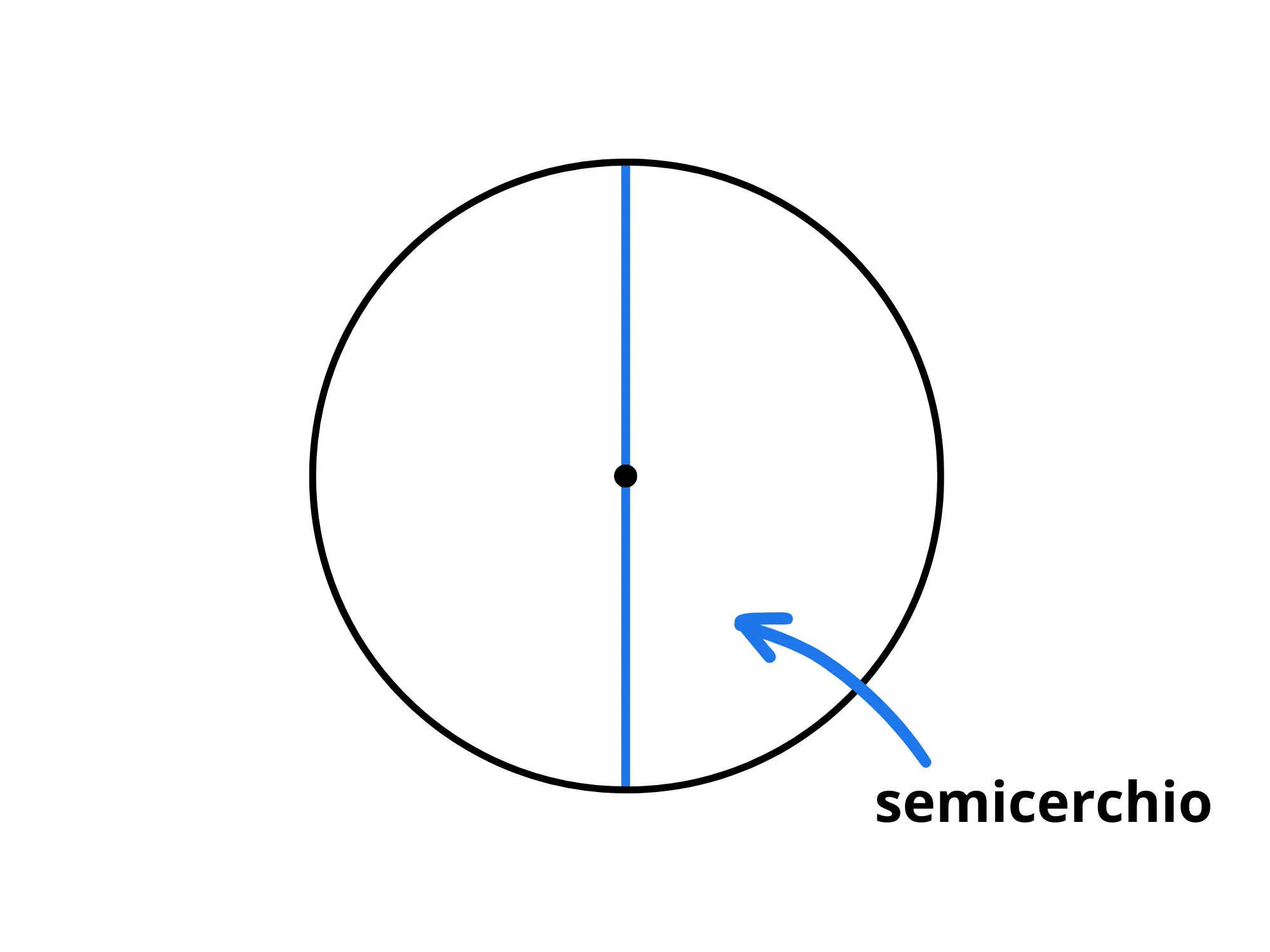
Se dividiamo il cerchio in due parti uguali, ognuna di esse viene chiamata semicerchio :

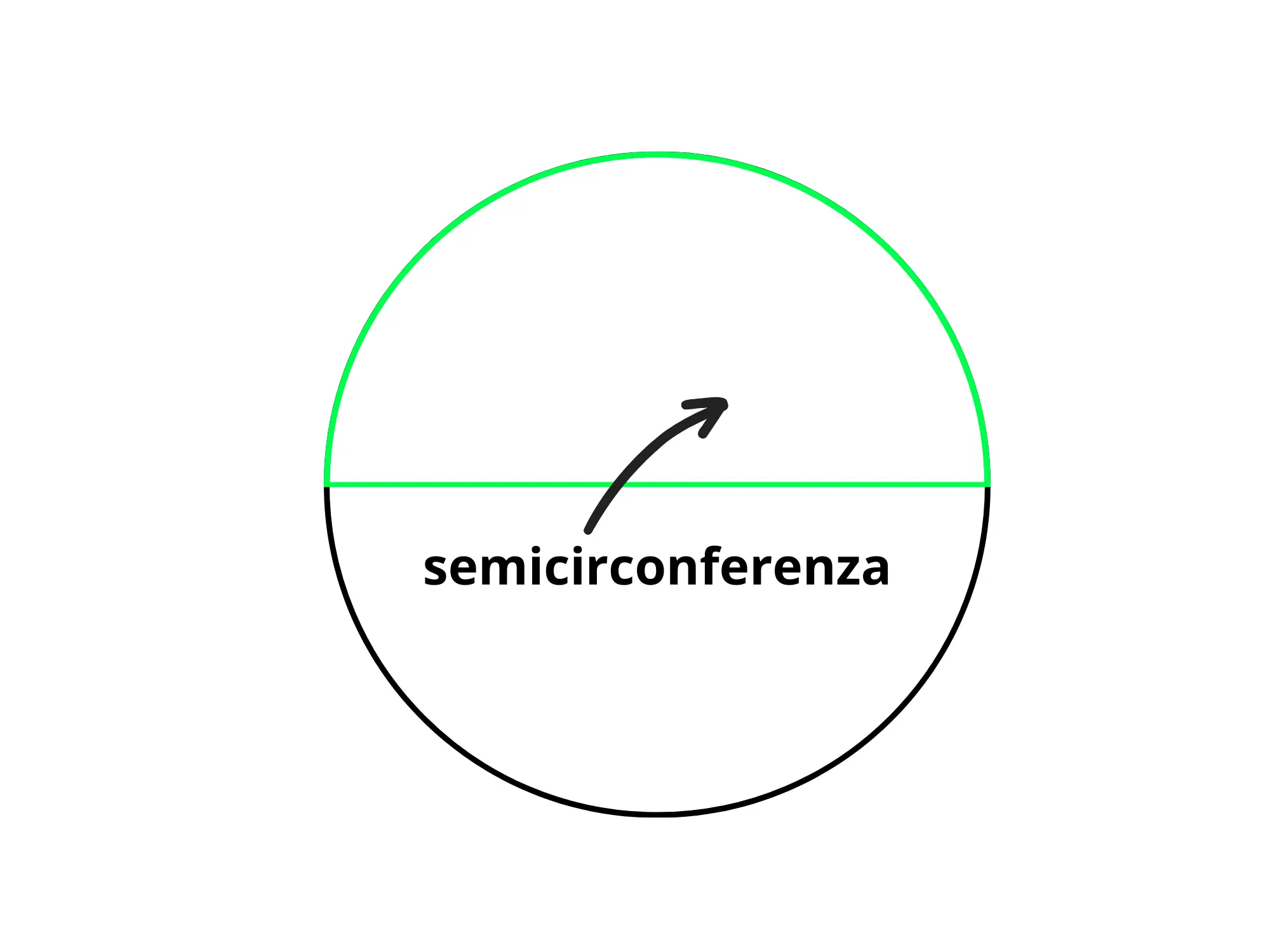
Se invece è la circonferenza ad essere divisa a metà, otteniamo due semicirconferenze :

Ora siamo pronti a studiare alcuni teoremi sul cerchio:

Teoremi sul cerchio

Iniziamo con una proprietà piuttosto nota:

Per 3 punti non allineati passa una ed una sola circonferenza.

Ecco la prossima proprietà:

Ogni corda non passante per il centro è minore del diametro:

Proviamo a dimostrarla:

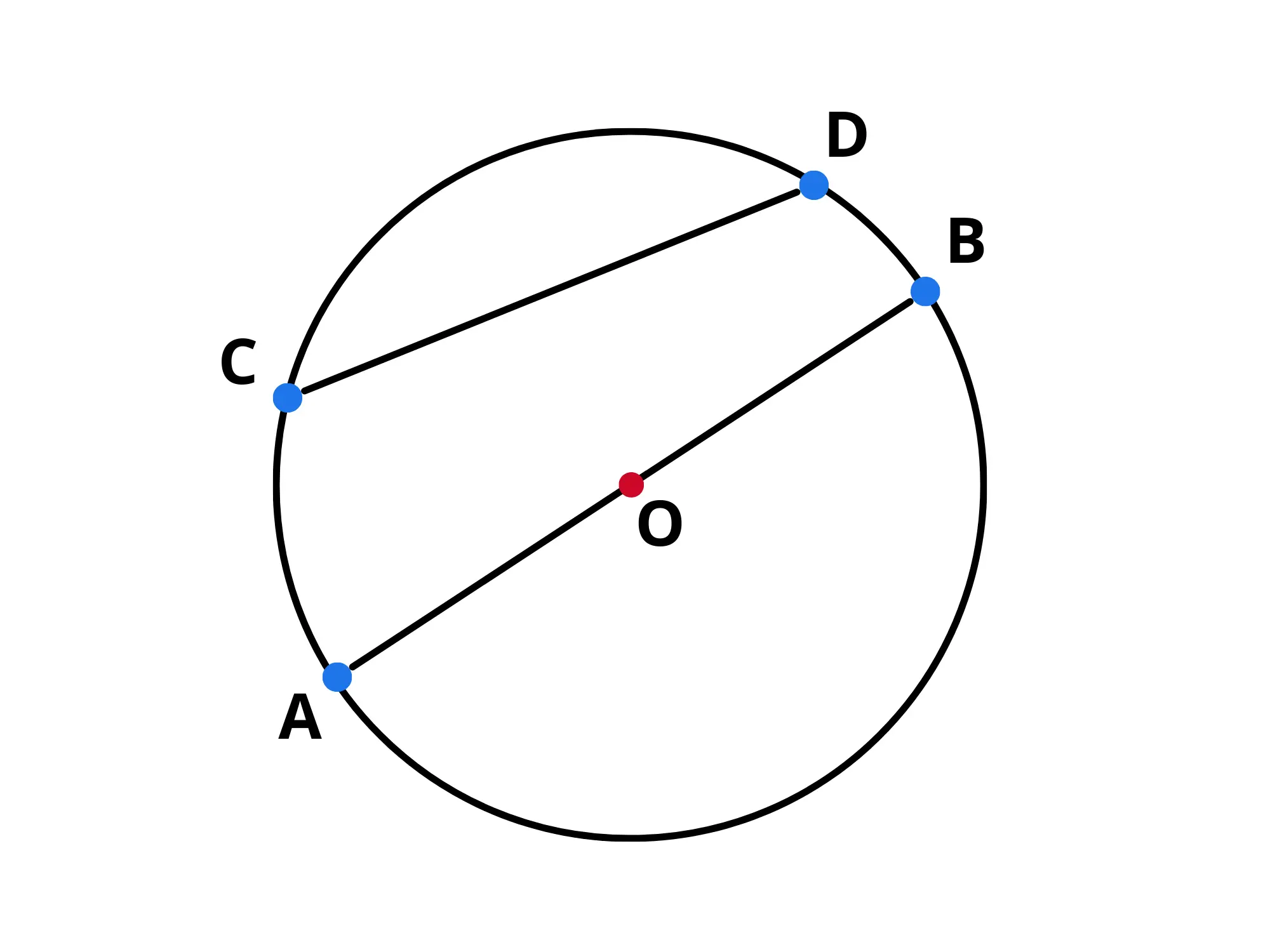
Abbiamo visto prima che il diametro $\displaystyle { d }$ equivale a due volte il raggio:

Tracciamo ora i due raggi che congiungono i punti $\displaystyle { C }$ e $\displaystyle { D }$ con il centro $\displaystyle { O }$ :

Guardiamo ora al triangolo $\displaystyle { \overset{\triangle}{COD} }$ che abbiamo costruito:

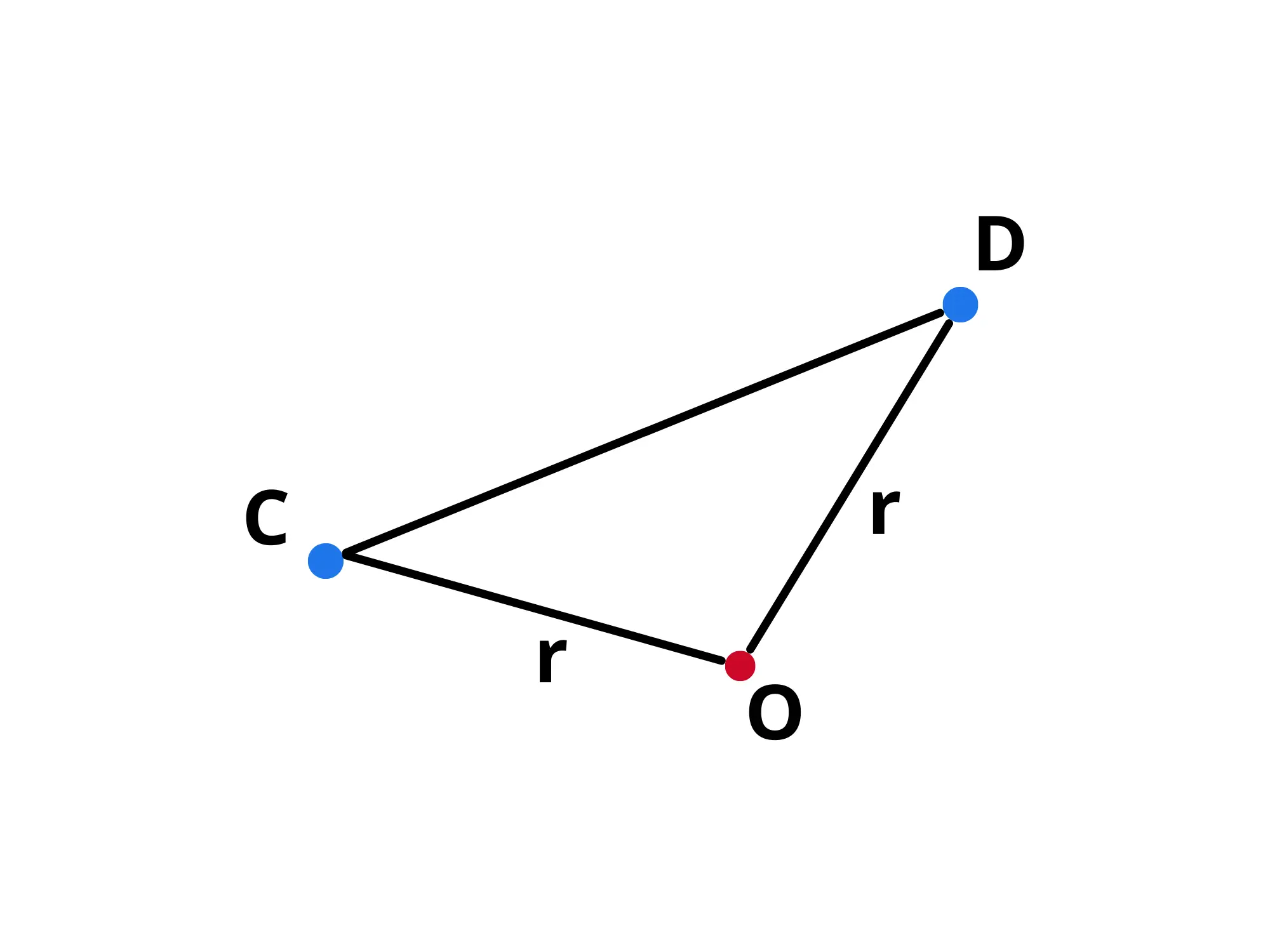
Sappiamo che in un triangolo, la somma di due lati deve sempre essere maggiore del terzo lato (disuguaglianza triangolare). Dunque dovremo avere:

$\displaystyle { \overline{CD} < \overline{CO} + \overline{DO} }$

I due segmenti a destra, però, sono dei raggi del cerchio, dunque avremo:

$\displaystyle { \overline{CD} < r + r }$

$\displaystyle { \overline {CD} < 2r }$

Ed abbiamo detto che il diametro è uguale a $\displaystyle { 2r, }$ dunque avremo:

$\displaystyle { \overline{CD} < d }$

Cioè qualsiasi corda non passante per il centro è minore del diametro (bisogna aggiungere che la corda non passa per il centro perché altrimenti tracciando i raggi non si otterrebbe un triangolo ed infatti tutti i diametri sono uguali).

Passiamo al prossimo teorema:

La perpendicolare condotta per il centro della circonferenza ad una corda la divide a metà:

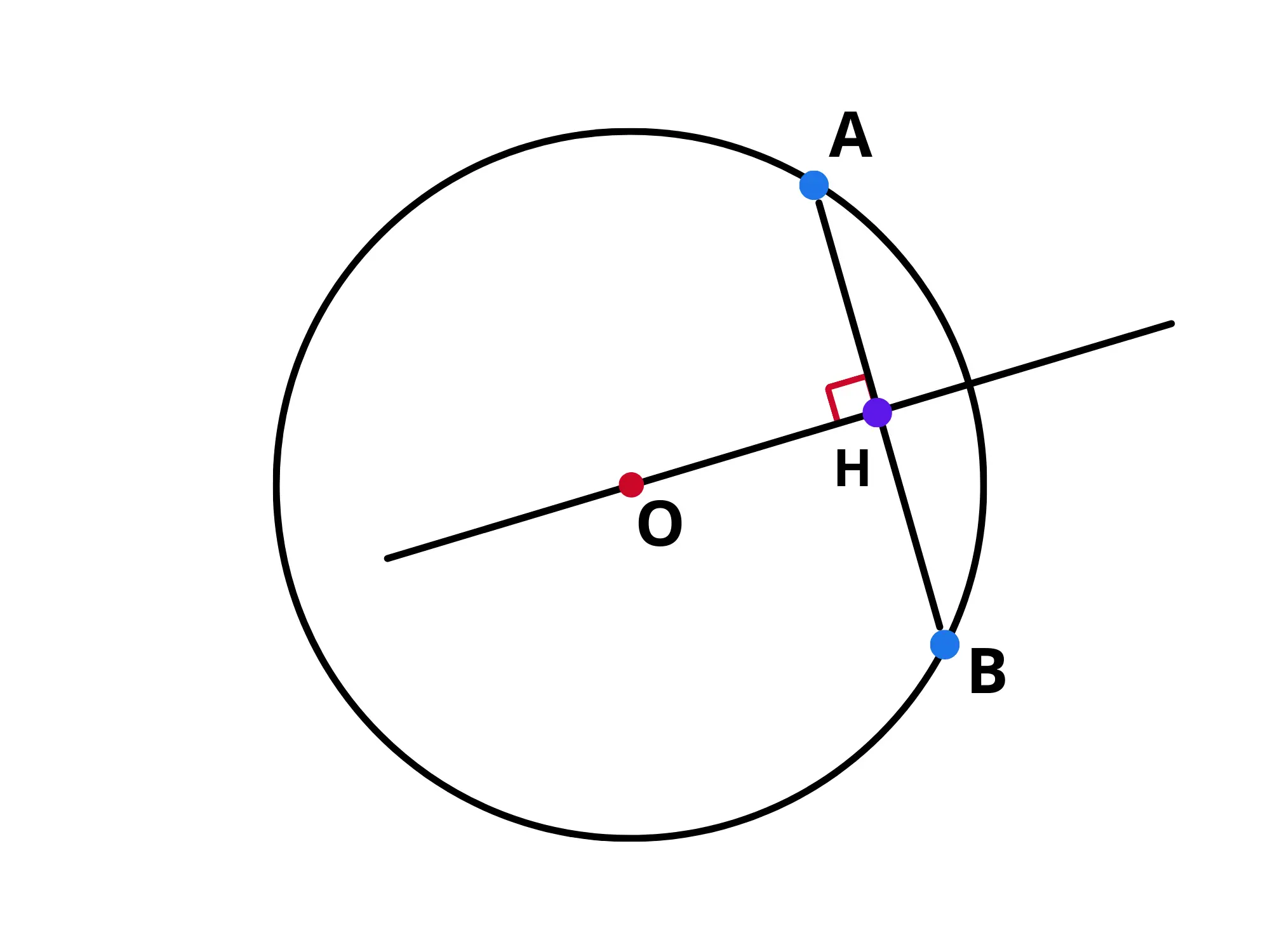
Dunque avremo che $\displaystyle { \overline{AH}=\overline{HB}. }$ Per dimostrarlo, tracciamo anche questa volta i raggi che congiungono i due punti $\displaystyle { A }$ e $\displaystyle { B }$ con il centro $\displaystyle { O }$ :

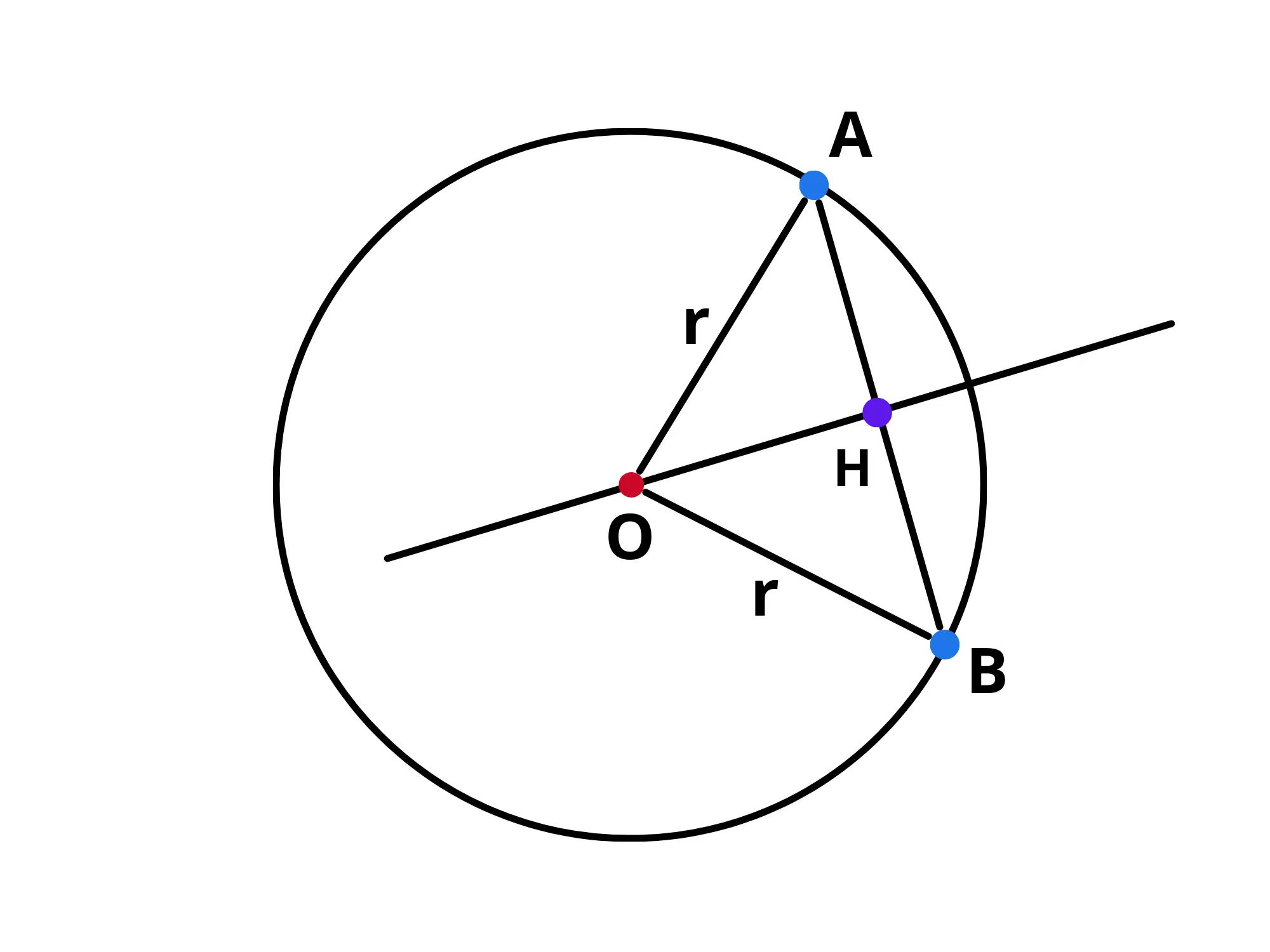
Guardiamo ora al triangolo $\displaystyle { \overset{\triangle}{AOB}: }$

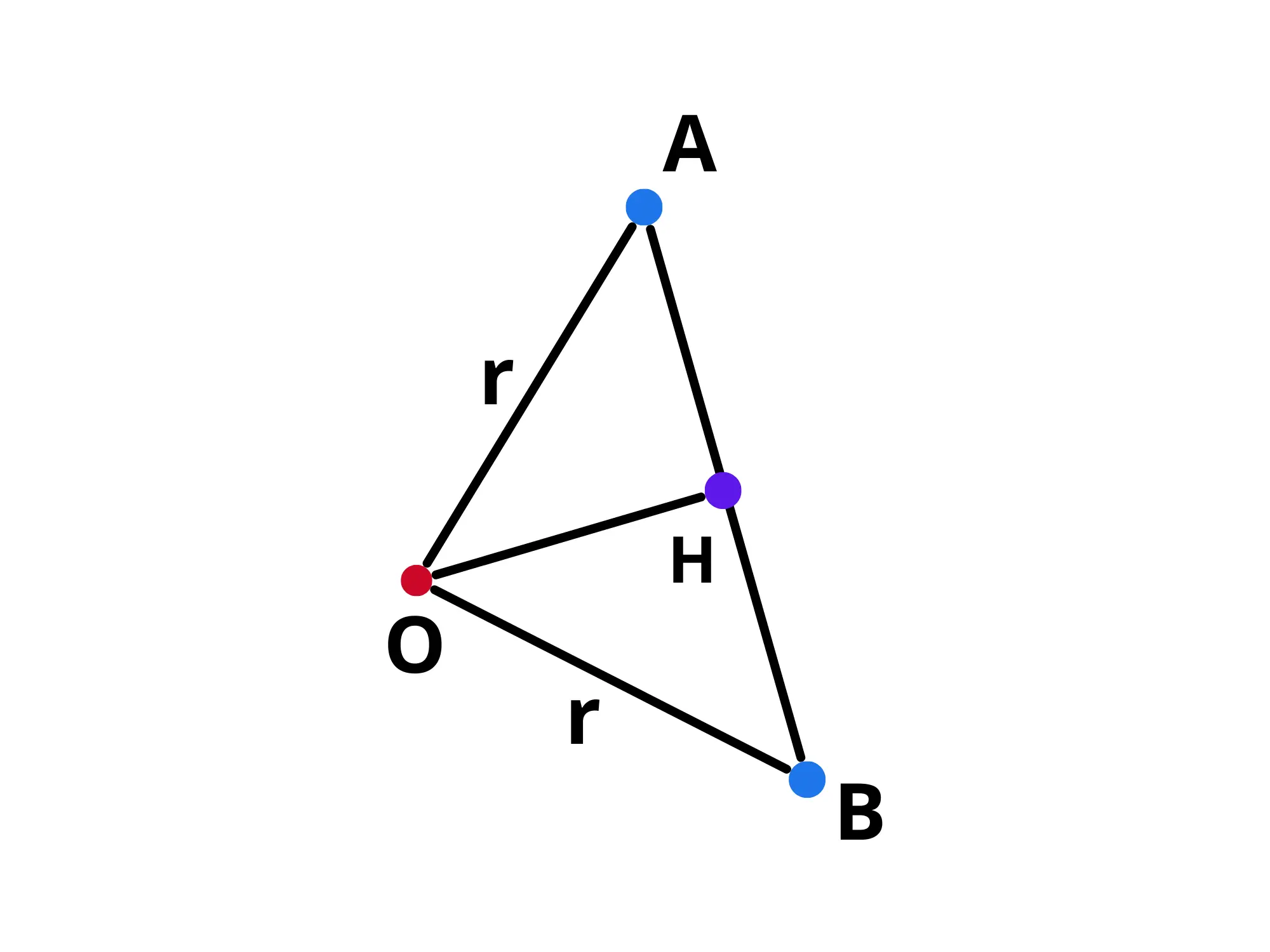
Siccome sia $\displaystyle { AO }$ che $\displaystyle { BO }$ sono lunghi $\displaystyle { r, }$ il triangolo dovrà essere isoscele con base $\displaystyle { AB. }$ Siccome l'altezza rispetto alla base di un triangolo isoscele è anche mediana e bisettrice, $\displaystyle { OH }$ dovrà essere la mediana di $\displaystyle { AB, }$ dividendolo dunque in due parti uguali, come volevasi dimostrare.

Cos'è invece un angolo al centro?

Un angolo che ha il vertice nel centro del cerchio viene chiamato angolo al centro.

L'angolo $\displaystyle { A\hat {O} B }$ è un angolo al centro e si dice che insiste sull'arco $\displaystyle { \overset{\Large\frown}{AB} }$ o che corrisponde all'arco $\displaystyle { \overset{\Large\frown}{AB}. }$

Ad un angolo al centro corrisponde uno ed un soltanto arco.

Ad angoli al centro congruenti corrispondono archi congruenti e viceversa:

Quindi, nel grafico qui sopra, se $\displaystyle { A\hat{O} B \equiv C\hat{O} D, }$ dobbiamo avere $\displaystyle { \overset{\Large\frown}{AB} \equiv \overset{\Large\frown}{CD}. }$

Un angolo alla circonferenza è un angolo che ha il vertice sulla circonferenza e i cui lati passano per la circonferenza:

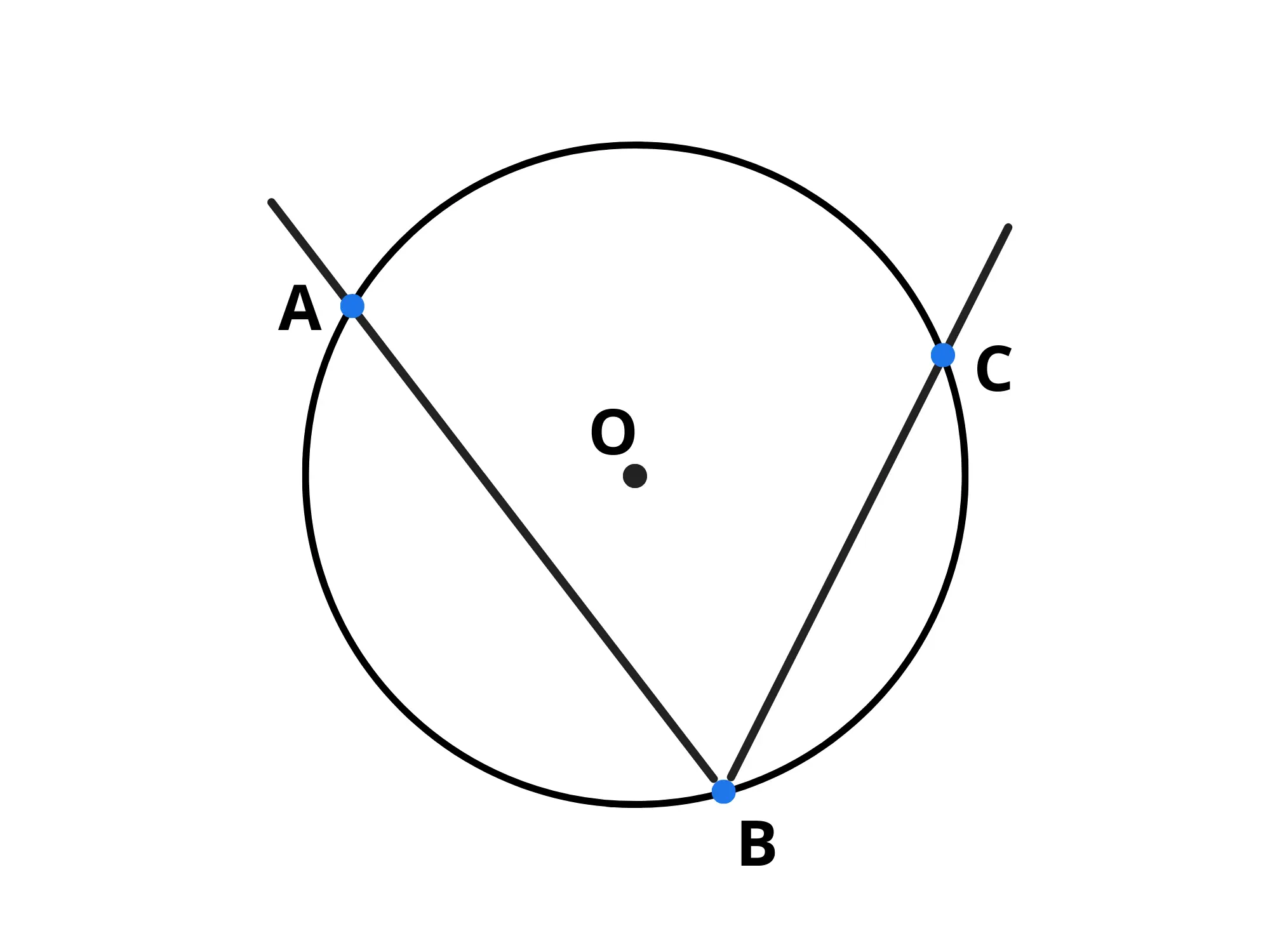
Nel grafico qui sopra, dunque, l'angolo $\displaystyle { \hat{ABC} }$ è un angolo alla circonferenza. Come per gli angoli al centro, anche in questo caso si dice che $\displaystyle { A\hat{B}C }$ insiste sull'arco $\displaystyle { \overset{\Large\frown}{AC} }$ e due angoli alla circonferenza sono uguali se e solo se insistono su archi congruenti.

Ora siamo pronti per enunciare uno dei teoremi più importanti della lezione:

Un angolo alla circonferenza è sempre la metà dell'angolo al centro che insiste sul suo stesso arco:

Abbiamo quindi $\displaystyle { A\hat{O}B=2A\hat{C}B. }$

Da questo consegue che ogni triangolo inscritto in una semicirconferenza è un triangolo retto:

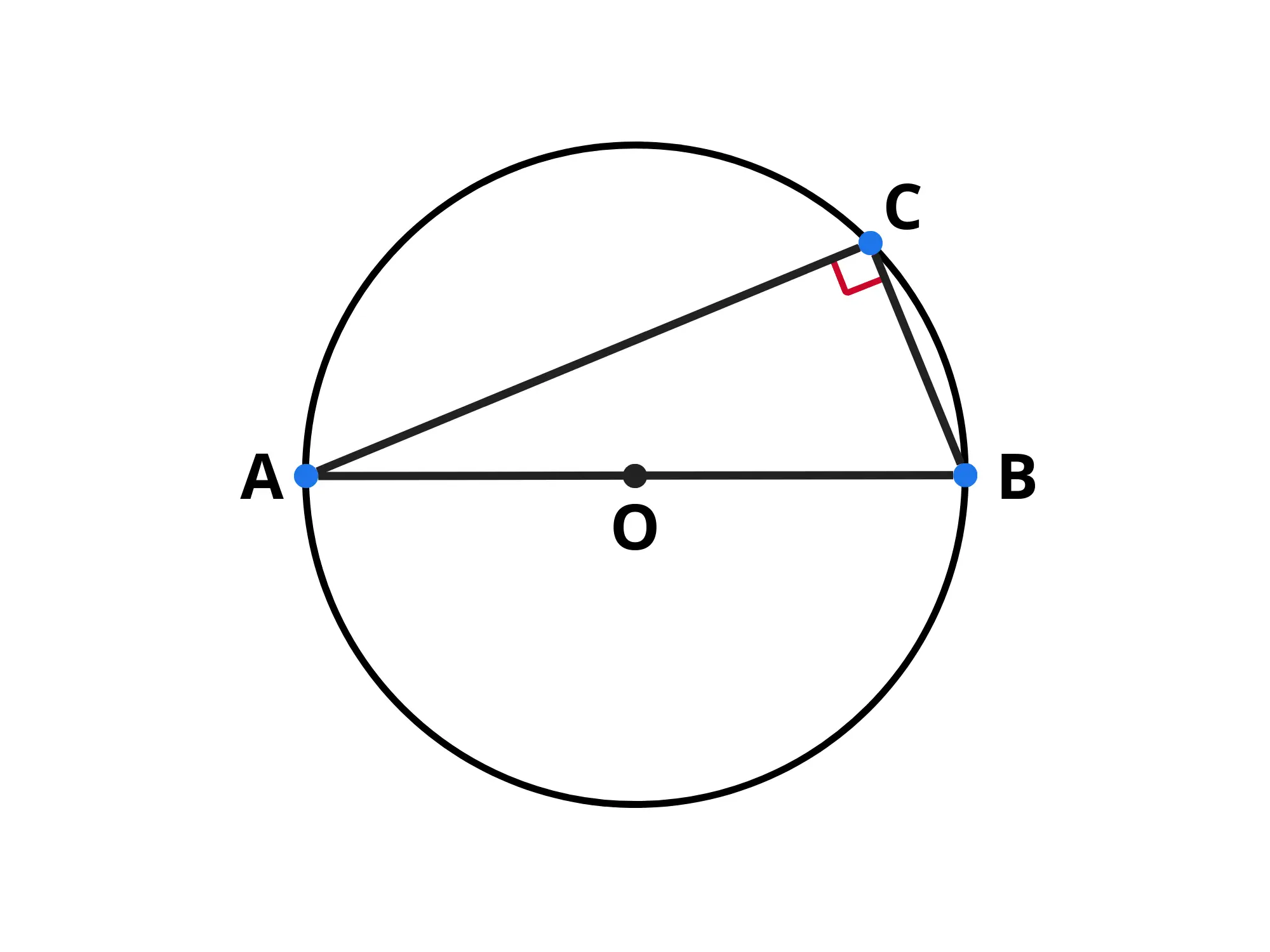
Questo perché sia l'angolo $\displaystyle { A\hat{C}B }$ che $\displaystyle { A\hat{O}B }$ insistono sull'arco $\displaystyle { \overset{\Large\frown}{AB} }$ e il primo è un angolo alla circonferenza e il secondo un angolo al centro. Dunque, per il teorema di prima, dobbiamo avere:

$\displaystyle { A\hat{O}B=2A\hat{C}B }$

$\displaystyle { A\hat{C}B= {A\hat{O}B\over 2} }$

I punti $\displaystyle { A,O }$ e $\displaystyle { B }$ sono allineati perché, per costruzione, $\displaystyle { AB }$ deve essere un diametro e dunque $\displaystyle { A\hat{O}B }$ deve essere un angolo piatto.

Quindi $\displaystyle { \hat{ACB} }$ è la metà di un angolo piatto, cioè un angolo retto, perciò il triangolo $\displaystyle { \overset{\triangle}{ABC} }$ è retto in $\displaystyle { C. }$

Passiamo al prossimo teorema:

Prendiamo un punto $\displaystyle { P }$ e tracciamo le due tangenti al cerchio da $\displaystyle { P }$ che identificheranno i due punti di tangenza $\displaystyle { B }$ e $\displaystyle { C: }$

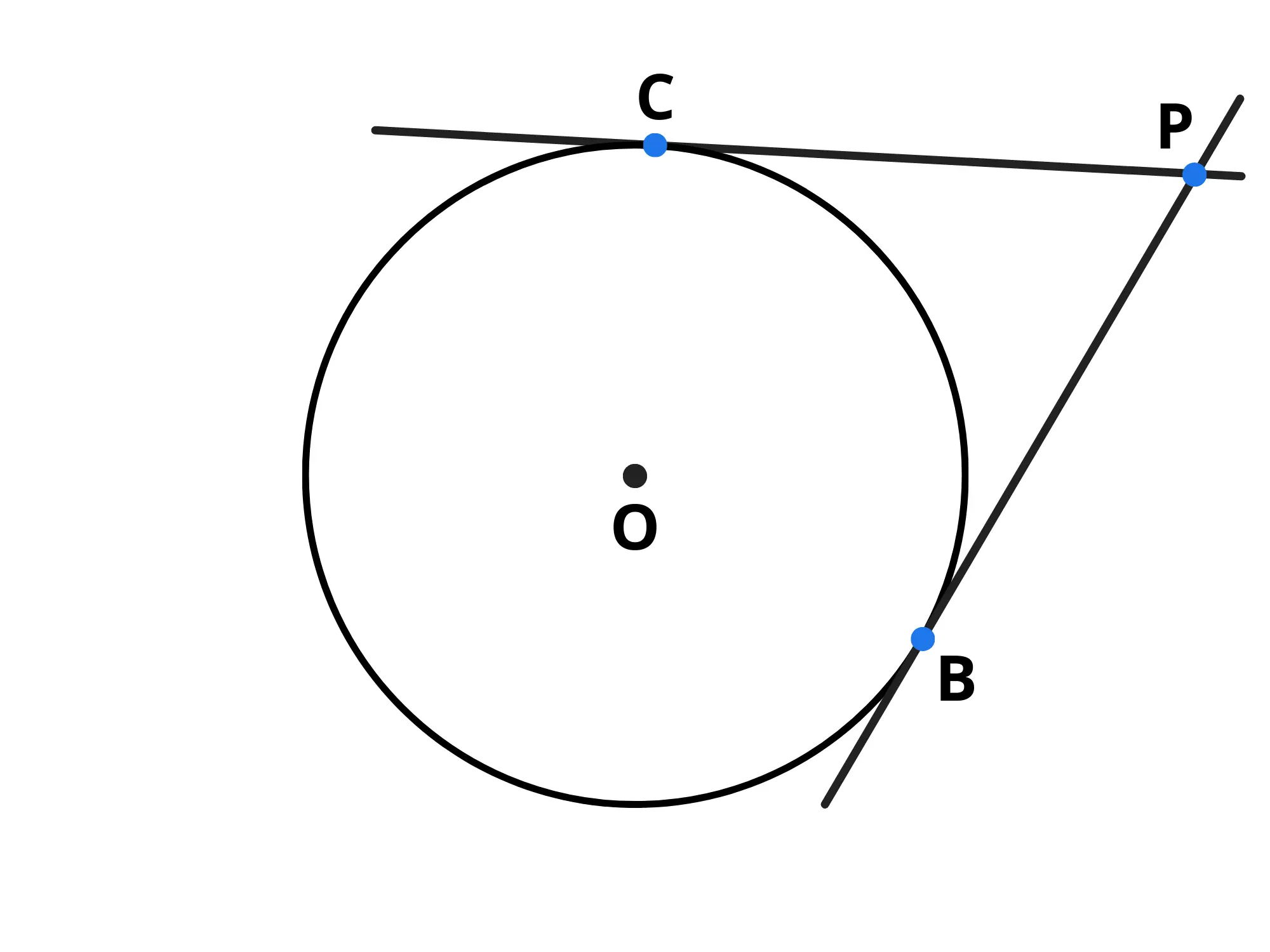
Adesso dimostriamo che i due segmenti $\displaystyle { BP }$ e $\displaystyle { CP }$ sono congruenti:

Tracciamo i raggi che congiungono i punti di tangenza $\displaystyle { B }$ e $\displaystyle { C: }$

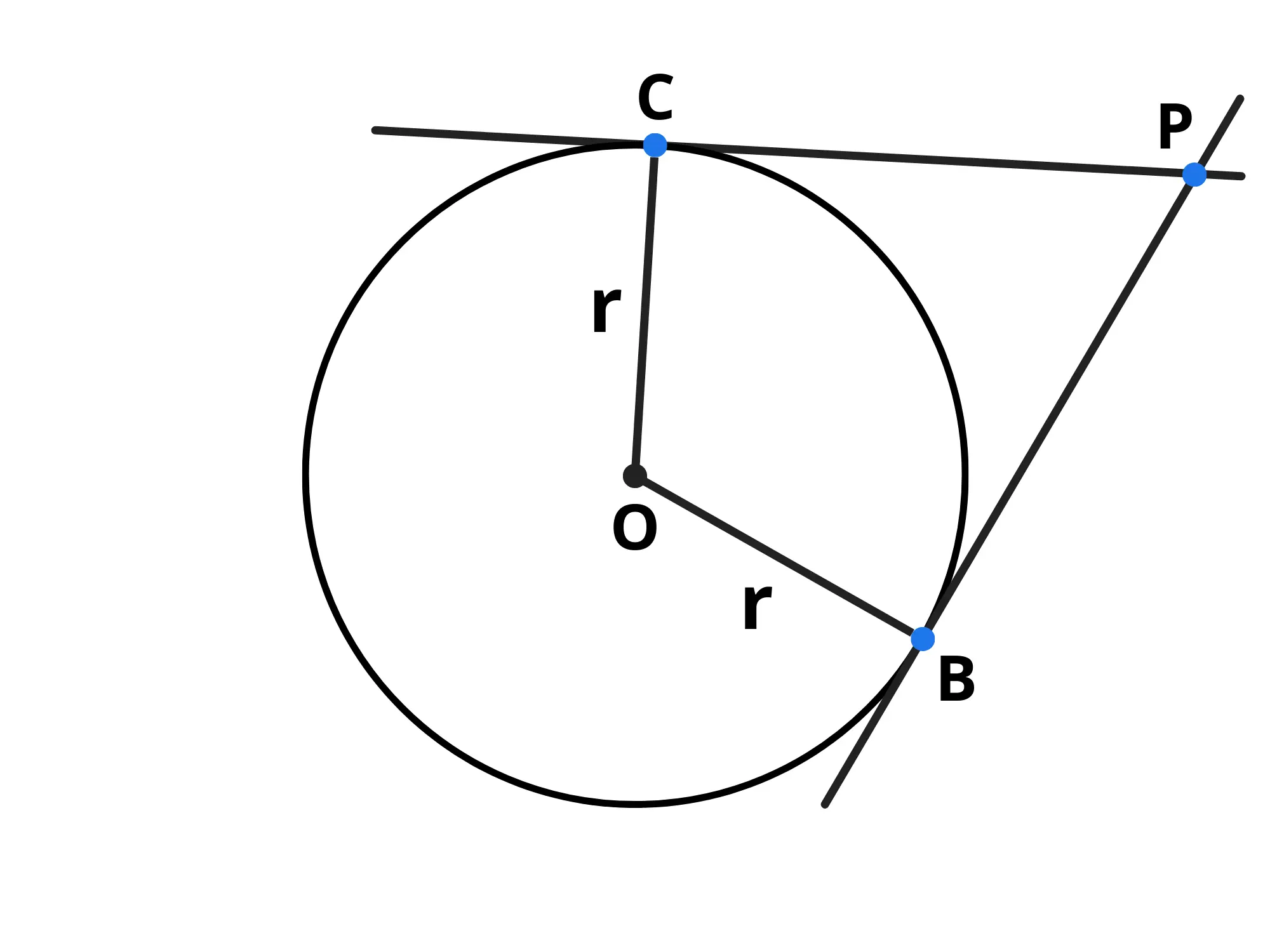
Tracciamo pure il segmento $\displaystyle { OP: }$

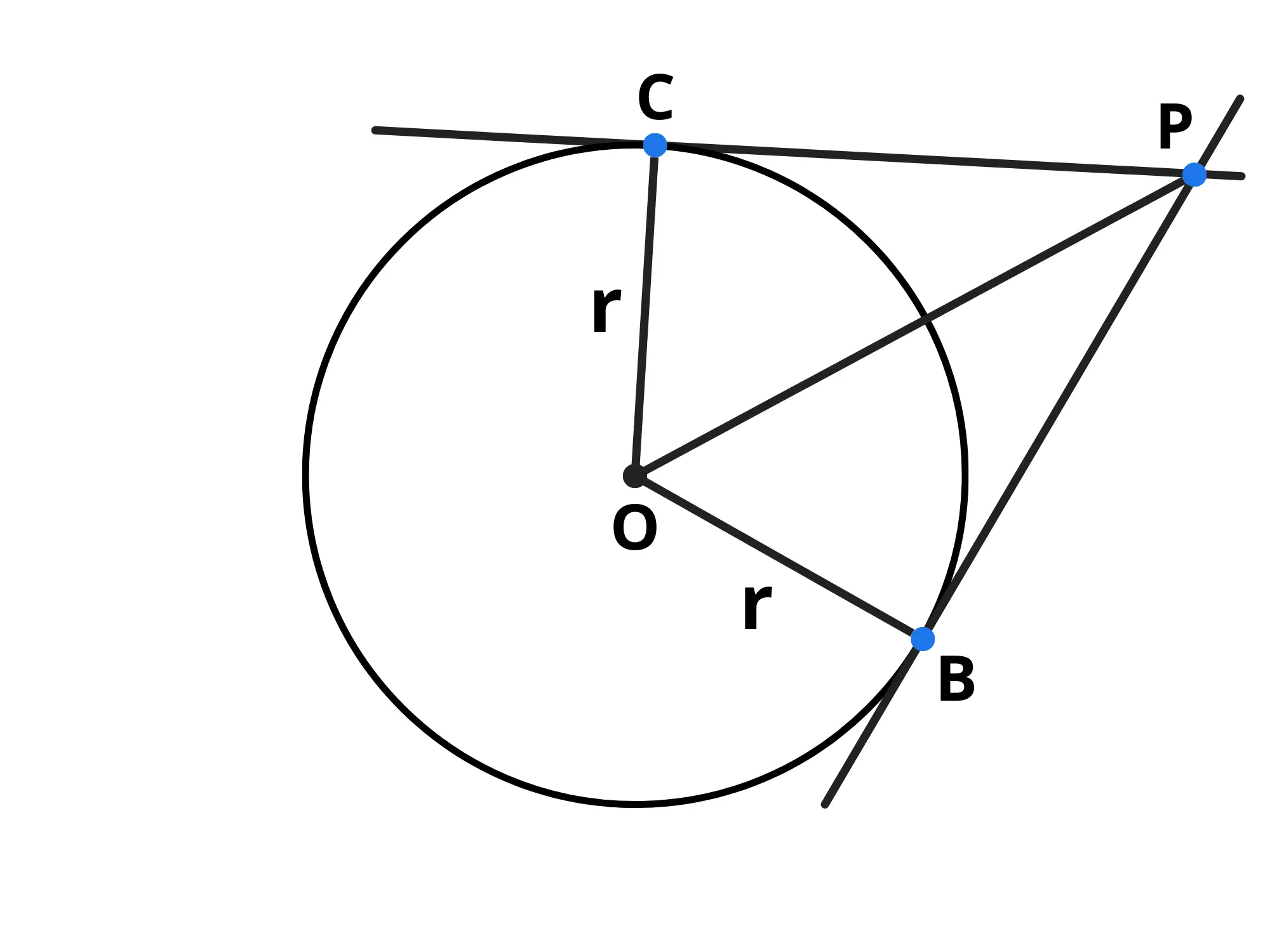
Il raggio è sempre perpendicolare alla retta tangente, dunque entrambi i triangoli $\displaystyle { \overset{\triangle}{BPO} }$ e $\displaystyle { \overset{\triangle}{CPO} }$ sono triangoli rettangoli:

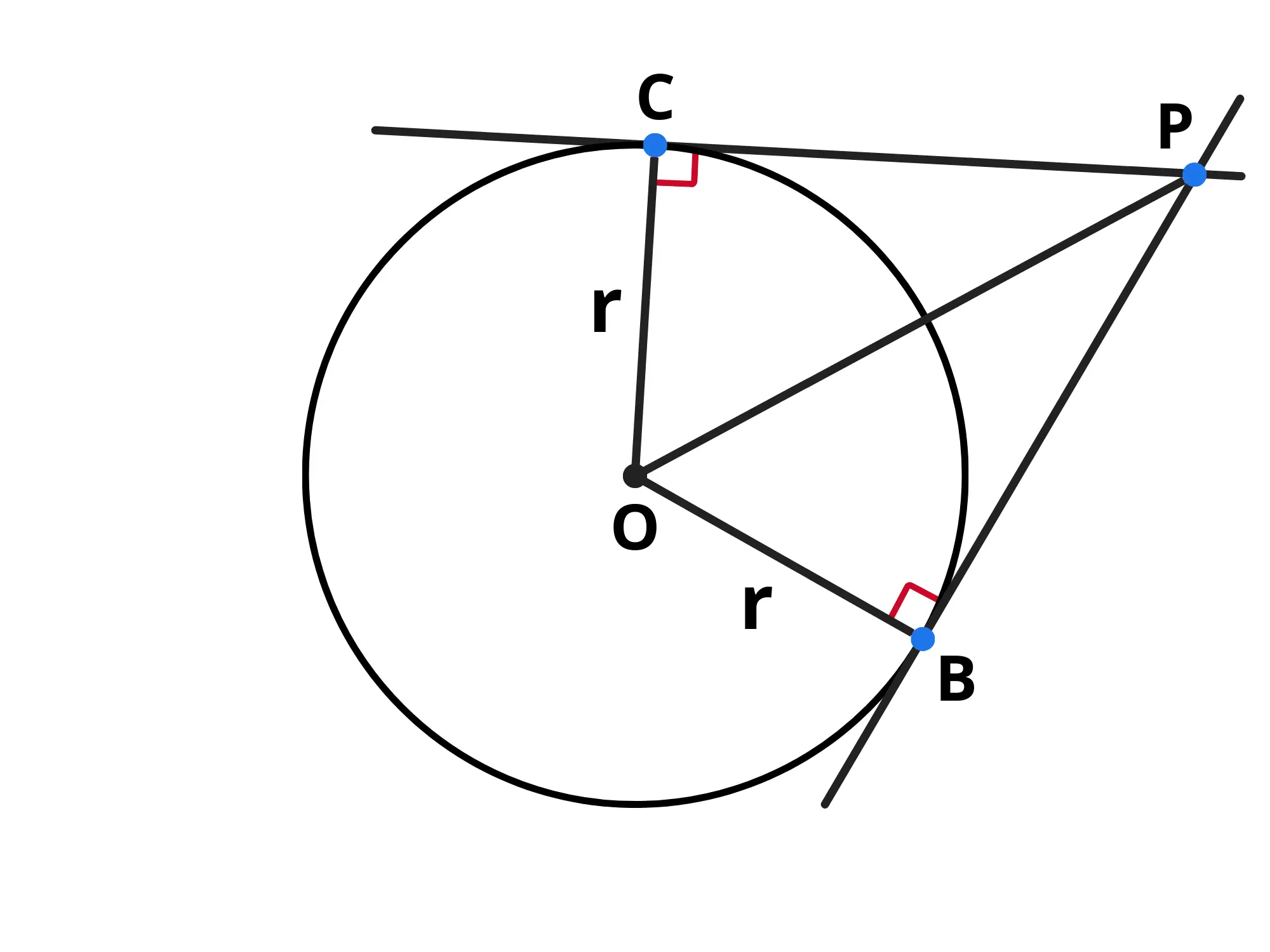
I triangoli $\displaystyle { \overset{\triangle}{BPO} }$ e $\displaystyle { \overset{\triangle}{CPO} }$ hanno in comune il lato $\displaystyle { OP }$ e i lati $\displaystyle { OB }$ e $\displaystyle { OC }$ sono uguali perché sono due raggi. Possiamo utilizzare il teorema di Pitagora ed ottenere che:

$\displaystyle { BP = \sqrt{OP^2 - OB^2} }$

Abbiamo però detto che $\displaystyle { OB = OC, }$ quindi possiamo sostituirlo:

$\displaystyle { BP = \sqrt{OP^2 - OC^2} }$

Questa radice a sinistra, però, sempre per il teorema di Pitagora, è uguale a $\displaystyle { CP, }$ dunque:

$\displaystyle { BP = CP }$

come volevasi dimostrare.

Vediamo quindi l'ultimo teorema della lezione:

Prendiamo un cerchio e tracciamo due corde incidenti:

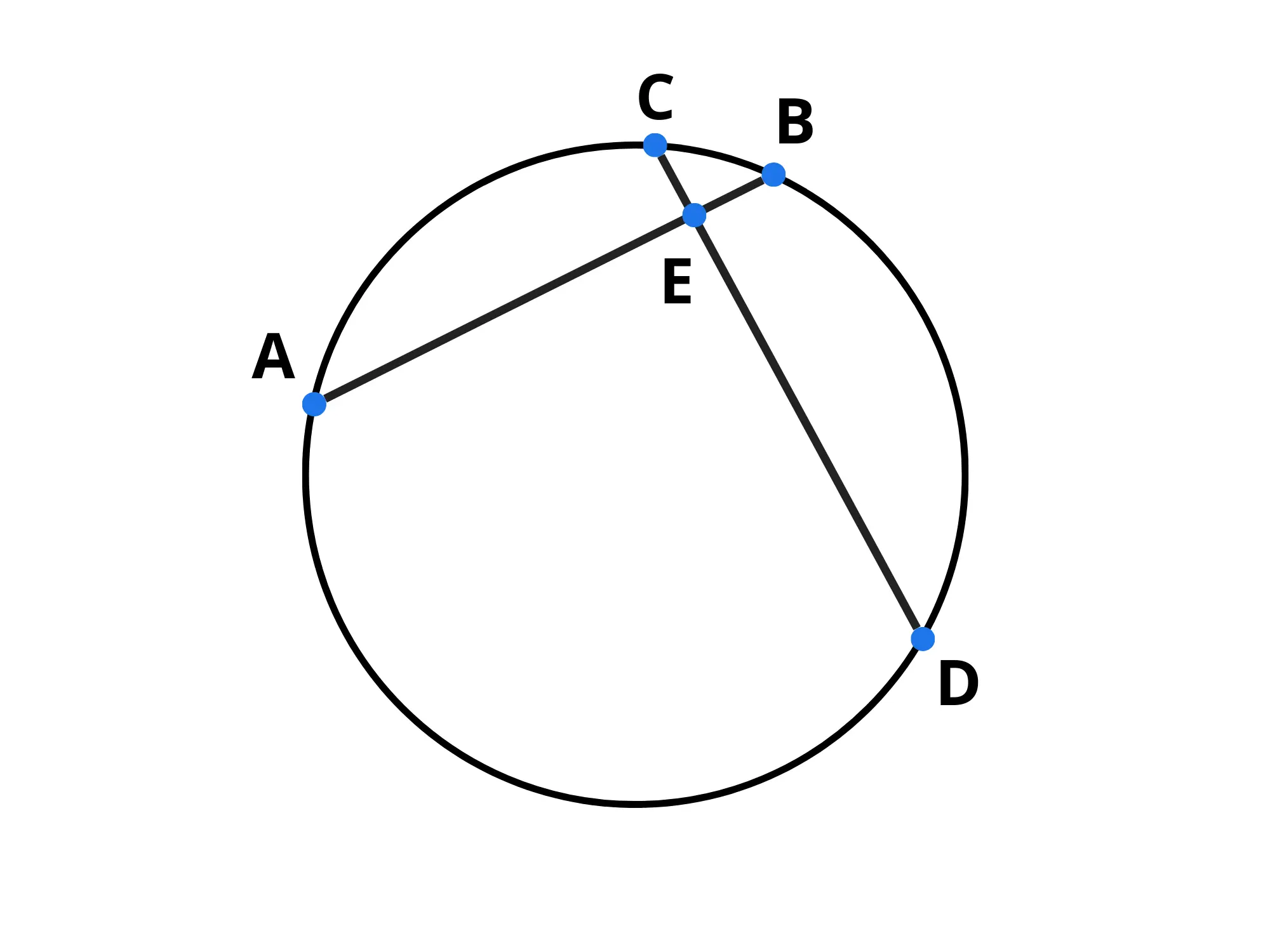
I segmenti che otteniamo rispettano la seguente proporzione:

Dimostriamolo! Tracciamo i segmenti $\displaystyle { AC }$ e $\displaystyle { DB: }$

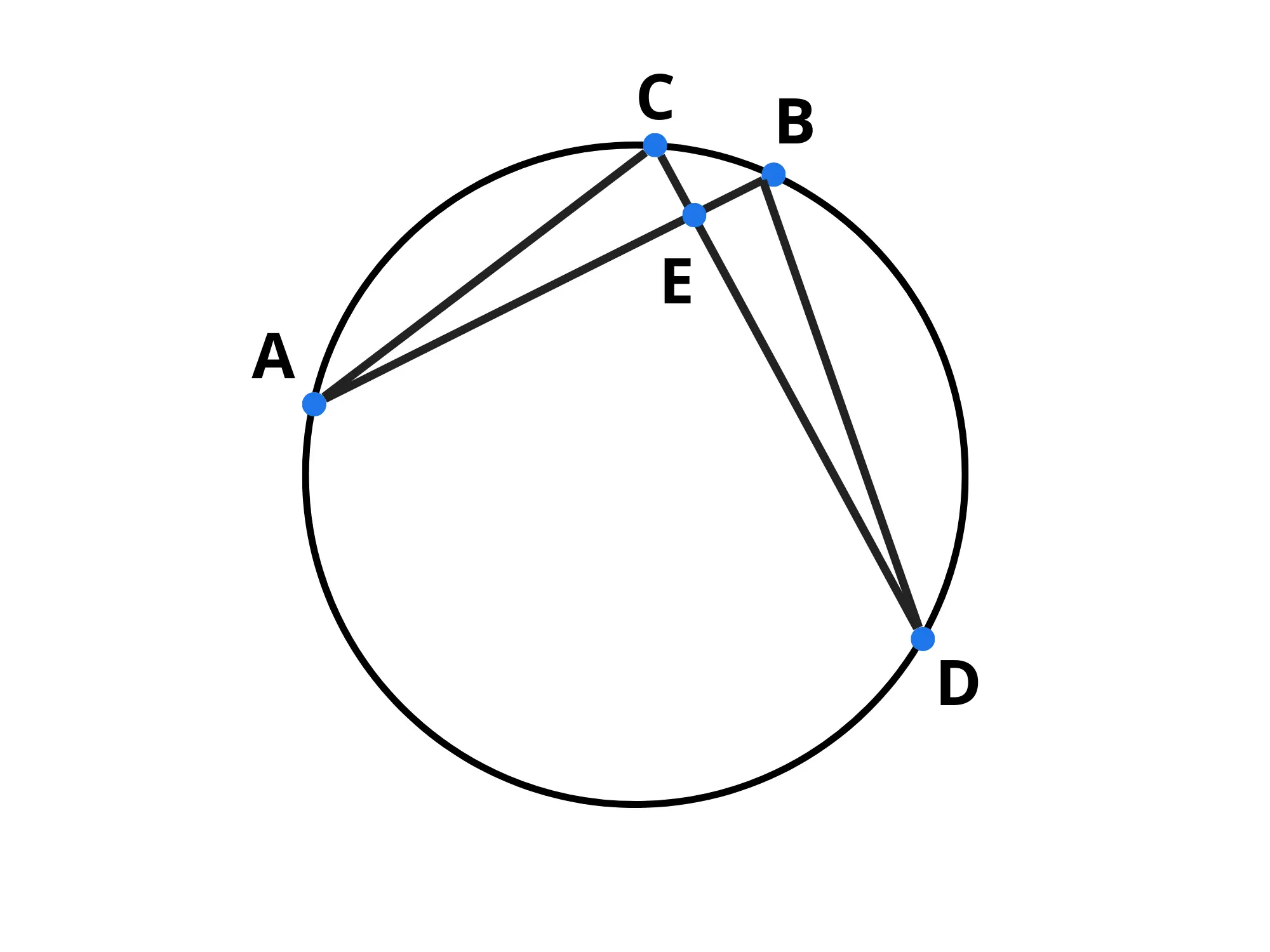
Siccome sono angoli al vertice, $\displaystyle { \hat{AEC}=\hat{DEB}. }$ Notiamo che gli angoli $\displaystyle { \hat{ACD} }$ e $\displaystyle { \hat{ABD} }$ sono angoli alla circonferenza che insistono sullo stesso arco, dunque devono essere uguali.

Siccome i triangoli $\displaystyle { \overset{\triangle}{AEC} }$ e $\displaystyle { \overset{\triangle}{DEB} }$ hanno quindi due angoli uguali, devono essere due triangoli simili. Il rapporto dei lati corrispettivi devono essere uguale, perciò:

$\displaystyle { {AE\over DE} = {EC\over EB} }$

Riscrivendola con la notazione della proporzione otteniamo proprio quello che volevamo dimostrare: